基于混沌优化MPSO的移动机器人FastSLAM算法研究
2015-10-28朱奇光夏翠萍陈卫东
朱奇光 夏翠萍 陈卫东 陈 颖
1.燕山大学,秦皇岛,0660042.河北省特种光纤与光纤传感重点实验室,秦皇岛,066004
基于混沌优化MPSO的移动机器人FastSLAM算法研究
朱奇光1,2夏翠萍1陈卫东1,2陈颖1
1.燕山大学,秦皇岛,0660042.河北省特种光纤与光纤传感重点实验室,秦皇岛,066004
针对移动机器人快速同时定位和地图创建(FastSLAM)中粒子退化问题,提出一种基于混沌优化的中值导向粒子群优化(MPSO)算法。该算法在粒子估计过程中引入观测信息,调整粒子的提议分布,提高位置预测的准测性。混沌优化MPSO算法采用两步优化策略,首先通过中值导向加速度来改进粒子的进化速度,有效地克服粒子退化问题,改善算法的收敛性;然后针对粒子耗尽问题,在MPSO优化算法中引入混沌搜索算法来寻找全局最优位置,驱散聚集在局部最优的粒子群,使其向全局最优位置靠近,扩大解空间的范围,从而保持种群的多样性。仿真和实时数据证明了该方法正确、可行。
快速同时定位和地图创建;提议分布;中值导向粒子群优化;中值导向加速度;混沌
0 引言
移动机器人同时定位与地图创建(simultaneous localization and mapping, SLAM)是指移动机器人在未知环境中运动时,构建增量式地图的同时自我定位的过程[1]。扩展卡尔曼滤波(extend Kalman filter, EKF)通过增量式数据来评估机器人位姿和环境特征位置的联合后验概率,被广泛应用于移动机器人SLAM中。但基于EKF的SLAM存在两个明显的缺陷[2]:一是其计算复杂度高,导致特征数目不能太多,数据处理也极其复杂;二是如果数据关联一旦错误则EKF滤波器将发散。针对此局限,Montemerlo等[2-3]提出了快速同时定位与地图创建(FastSLAM)算法,将SLAM后验概率降解为定位问题和基于机器人位姿的K个独立环境特征的评估问题。但在标准FastSLAM方法中,基于序列重要性采样(sequential impotance sampling, SIS)存在粒子退化问题[4],重采样虽然可以解决退化问题,但由于权重大的采样多次被复制,权重小的采样被忽略,所以这样又导致了粒子的耗尽现象。目前很多学者致力于改进FastSLAM算法,Yoon等[5]提出了模糊粒子滤波器算法,该方法可以克服样本中干扰粒子对预测结果的影响,从而提高预测结果的精度,但是实现起来比较复杂。刘利枚等[6]将粒子群优化(particle swarm optimization, PSO)的思想引入到粒子滤波中,有效地改善了粒子的退化问题,但不能有效地解决粒子的耗尽问题。
针对FastSLAM中粒子退化耗尽问题,本文提出了一种基于混沌MPSO(median-oriented PSO)优化的FastSLAM算法,该算法利用机器人的观测值对预测采样过程进行优化,从而增强位置预测的准确性,并且通过调整该算法的结构,有效地解决了粒子退化问题。针对粒子的耗尽问题,采用混沌搜索算法对其进行优化,可以在迭代中产生许多局部最优解的邻近点, 以此来帮助惰性粒子逃离局部最优点, 进而能够快速搜寻到全局最优点,很好地保持了粒子的多样性。
1 改进的粒子群优化算法
PSO算法[7]是一种基于群体智能的全局优化算法,它利用m个粒子组成的粒子群在n维目标空间中搜索最优解。粒子i具有两个属性:位置xi=(xi1,xi2,…,xin)T与速度vi=(vi1,vi2,…,vin)T,其中xi为一个潜在解。粒子曾经历过的最好位置(个体最优位置)为ppbest=(pp1,pp2,…,ppn)T和整个群体曾经历过的最好位置(全局历史最优位置)为pgbest=(pg1,pg2,…,pgn)T。每次迭代中,粒子i第d维的速度和位置按下式更新:
vid(t+1)=w(t)vid(t)+C1r(pid(t)-xid(t))+
C2r(pgd(t)-xid(t))
(1)
xid(t+1)=xid(t)+vid(t+1)
(2)
d=1,2,…,ni=1,2,…,m
式中,t为当前进化代数;r为分布于[0,1]之间的随机数;C1、C2为加速常数;w(t)为惯性权重;xid(t)为当前位置;pid为局部最优位置;pgd(t)为全局最优位置。
1.1中值导向PSO算法
在PSO中,粒子群在追逐最优粒子时,越接近最优粒子,其速度越小,粒子群表现出强烈的趋同性,容易陷入局部最优,特别当似然函数呈多峰状态时,会使大量粒子聚集在次优位置,无法到达最优位置,使得其并不能有效地改善粒子退化与枯竭现象,从而影响算法的精确度。为了避免粒子的退化枯竭现象,本文对PSO算法的结构进行了优化和改进,从而提出了一种中值导向的粒子群优化(median-oriented particle swarm optimization, MPSO)算法。
该算法如下:
vid(t+1)=vid(t)+Mid(t)
(3)
其中,Mid(t)代表中值导向加速度,其定义如下:
Mid(t)=ai(t)[r(pid(t)-pmd(t)-xid(t))+
r(pgd(t)-pmd(t)-xid(t))]
(4)
则每次迭代中,粒子i第d维的更新速度公式为
vid(t+1)=vid(t)+ai(t)[r(pid(t)-pmd(t)-
xid(t))+r(pgd(t)-pmd(t)-xid(t))]
(5)
其中,pmd(t)为d维空间中粒子当前中间位置,ai(t)为加速系数,且
(6)
(7)
其中,fi(t)为第i个粒子适应度,fmax(t)和fmed(t)分别为当前粒子适应度最大值和适应度中间值:
fmax=max(fj(t))
(8)
fmed(t)=median(fj(t))
(9)
由经典牛顿力学可知,一个向量粒子在Δt时间内受到恒定的加速度时有
(10)
式中,x1和x2分别为最初位置和最后位置;a和v1分别为粒子的加速度和初速度。
把式(5)代入式(2)中,并根据牛顿经典力学公式(式(10))可推出每次迭代中,粒子i第d维的更新位置公式:
xid(t))+r(pgd(t)-xid(t))]
(11)
在粒子群优化算法中,中值导向加速度扮演了一个关键角色,不仅提高了算法的收敛速度,而且还可以帮助粒子逃离局部最优。当粒子远离机器人真实位姿时,改进后的粒子群算法将有助于粒子向机器人真实的位置移动,从而提高机器人位置估计的精确性。在标准的PSO中,随着优化的进行,线性递减的惯性权重w可以平衡粒子局部开发能力和全局探测能力[8]。而在MPSO中,中值导向加速度可以更好地权衡粒子的开发和探测能力。
1.2利用混沌对MPSO进行优化
混沌具有遍历性、随机性和规律性等特点,能够在一定范围内按照自身的规律不重复地遍历所有的状态,具有易跳出局部最优、搜索速度快、全局渐近收敛等优点[9]。而在MPSO算法中,随着搜索迭代的进行,种群多样性不断损失,使得算法有可能过早收敛,因此在MPSO算法中引入混沌搜索算法来寻找全局最优位置,驱散聚集在局部最优的粒子群,使其向全局最优位置靠近,扩大解空间范围,从而保持种群的多样性,提高算法的精确度[10]。
本文采用适应度方差作为判断粒子陷入局部最优的准则。设粒子群的数量为n,fi为第i个粒子的适应度,favg为粒子群的平均适应度, 则适应度方差的标准值为
(12)
粒子群体的适应度方差为
(13)
其中,ρ2反映粒子群体的收敛程度,ρ2越小,群体越接近收敛。根据实际情况设定一收敛阈值a,当ρ2 本文采用分段Logistic混沌映射初始化各粒子[11]: (14) 其中,xid(t+1)⊂(0,1),初值xid(t)取0.345,u是控制参量,当u=4时,系统完全处于混沌状态。与一般的Logistic或Tent混沌映射相比,式(14)产生的混沌序列在(0,1)间分布对称性较好,具有良好的随机性和对初值敏感性,并且在生成混沌序列时无需进行扰动运算,使算法具有很高的效率。 利用式(14)产生的混沌序列进行混沌搜索: pgd=xgd+R(2xid(t)-1) (15) 其中,R为搜索半径,采用2种不同搜索半径进行搜索,一种是以pgd为中心进行的混沌搜索: R1=η pgd 其中,η为混沌搜索系数。 另一种是以原点为中心的混沌搜索: R2=ρ(xmax-xmin) 其中,xmax和xmin分别为解空间上下界,ρ为混沌搜索的收缩因子,以减小混沌搜索的范围,增加搜索精度,本文取ρ=1.1。 基于混沌MPSO的FastSLAM算法流程步骤如下: (1)预测。根据提议分布对当前粒子集进行预测采样,获得下一时刻的粒子st~p(st|st-1,ut),其中,st~p(st|st-1,ut)为符合马尔可夫的建议分布函数。 (2)混沌MPSO优化。 ③用式(13)产生的混沌序列进行混沌搜索: ④通过引用适应度函数ffitness来判断机器人预测位置的优化程度并计算路标观测的预测值ztpred: (16) (17) (3)权重计算。通过下式计算粒子的权重: (18) 通过混沌MPSO优化,粒子集在计算权重前就更加接近机器人的真实位置,从而使得权重计算更能体现粒子的分布情况,重采样过程更加有效,加速了粒子集的收敛,为下一时刻机器人的位置预测提供了一个更好的初始值。 (a)标准的FastSLAM2.0地图 (b)APSO-VI FastSLAM算法地图 (c)混沌MPSO FastSLAM算法地图图1 各种算法的匹配地图 为了验证所提出的基于混沌MPSO的FastSLAM算法的有效性,对基于混沌MPSO的FastSLAM算法、APSO-VI FastSLAM算法[12]以及标准的FastSLAM 2.0算法进行比较。移动机器人的仿真环境为80 m×80 m的平面矩形区域,环境中有37个特征点和11个路径点,分别用“*”和“o”表示。如图1所示。图1a为采用标准的FastSLAM2.0算法得到的地图,图1b为采用APSO-VI FastSLAM算法得到的地图,图1c为采用基于混沌MPSO的FastSLAM算法得到的地图。图2a、图2b分别为基于APSO-VI FastSLAM算法和混沌MPSO FastSLAM算法的特征点估计标准差误差图。 (a)APSO-VI FastSLAM算法 (b)混沌MPSO FastSLAM算法图2 两种算法的特征点估计标准差误差图 从图1可知,在特征点估计上,图1a明显比图1b和图1c契合度低,而图1c局部的特征点估计明显比图1b契合度高;同时移动机器人在自身位姿路径估计上,图1a明显没有图1b和图1c路径估计契合度高,对比图1b、图1c可知,在y轴(0,40 m)坐标上图1c比图1b的路径估计契合度明显要高。这意味着无论基于机器人自身位姿估计还是特征估计,基于混沌MPSO FastSL-AM算法的建图准确度最高。从图2可知,基于 APSO-VI FastSLAM算法的特征点估计误差为0.44 m,而基于混沌MPSO FastSLAM算法的特征点估计误差为0.28 m,较之前者特征匹配度提高了36.36%,因此基于混沌MPSO FastSLAM算法明显改善了机器人在特征估计和自身位姿估计上的精确性。 为进一步说明算法的性能,下面分别给出三种算法在x轴、y轴方向的定位误差,如图3所示。图3a、图3b和图3c分别表示为标准的FastSLAM2.0算法定位方向误差、APSO-VI FastSLAM算法定位方向误差和混沌MPSO FastSLAM定位方向误差。由图3可知,标准的FastSLAM算法x和y方向的误差最大值分别为1.8 m和1.15 m, APSO-VI FastSLAM算法x方向和y方向的误差最大值分别为0.6 m和0.5 m,基于混沌MPSO的FastSLAM算法x方向和y方向的误差最大值分别为0.45 m和0.3 m。 基于混沌MPSO的FastSLAM算法相对其他两种算法在x方向上误差分别降低了75%和25%,y方向上误差分别降低了74%和40%,可知基于混沌MPSO的FastSLAM算法性能得到了很大的改善。 (a)标准的FastSLAM2.0定位方向误差 (b)APSO-VI FastSLAM算法定位方向误差 (c)混沌MPSO FastSLAM定位方向误差图3 各种算法的定位误差图 表1 有效样本比较结果 常规的FastSLAM2.0算法由于在位置预测过程中没有考虑最新的观测数据,因此影响地图的精度,同时该算法存在粒子退化和耗尽问题。针对以上问题,提出一种基于混沌MPSO的FastSLAM算法。该算法在粒子估计过程中引入观测信息,调整粒子的提议分布,增加位置预测的准测性。通过中值导向加速度来改进粒子的进化速度,不仅提高了算法的计算速度,而且有效地克服了粒子的退化问题,改善了算法的收敛性,提高了建图的精度。针对粒子耗尽问题,在MPSO优化算法中引入混沌搜索算法来找全局最优位置,驱散聚集在局部最优的粒子群,使其向全局最优位置靠近,扩大解空间的范围,从而保持种群的多样性。实验仿真表明,该方法很大的提高了建图的精确性。 [1]陈卫东, 刘要龙, 朱奇光. 基于改进雁群PSO算法的模糊自适应扩展卡尔曼滤波的SLAM算法[J]. 物理学报,2013, 62(17): 170506. ChenWeidong,LiuYaolong,ZhuQiguang.FuzzyAdaptiveExtendedKalmanFilterSLAMAlgorithmBasedontheImprovedWildGeesePSOAlgorithm[J].ActaPhys.Sin., 2013, 62(17): 170506. [2]MontemerloM,ThrunS.SimultaneousLocalizationandMappingwithUnknownDataAssociationUsingFastSLAM[C]//RoboticsandAutomation.ProceedingICRA’03.IEEEInternationalConference.Germany, 2003: 1985-199. [3]MontemerloM,ThrunS.FastSLAM:aFactoredSolutiontoSimultaneoustoSimultaneousLocationandLocalizationandMapping[C]//ArtificialIntelligence,ProceedingsoftheNationnalConference.Canasa, 2002: 593-598.[4]DoucetA,GodsillS,AndrieuC.OnSequentialMonteCarloSamplingMethodsforBayesianFilter[J].StatisticsandComputing, 2000, 10(3): 197-208.[5]YoonCY,CheonMK,ParkM.ObjectTrackingfromImageSequencesUsingAdaptiveModelsinFuzzyParticleFilter[J].InformationSciences, 2013, 253(20): 74-99.[6]刘利枚, 蔡自兴. 基于改进的粒子群优化的FastSLAM方法[J]. 高技术通讯, 2011, 21(4): 422-427. LiuLimei,CaiZixing.AnApproachtoFastslamBasedonImprovedParticleSwarmOptimizationAlgorithm[J].ChineseHighTechnologyLetters, 2011, 21(4): 422-427.[7]KennedyJ,EberhartR.ParticleSwarmOptimization[C]//ProceedingsoftheIEEEInternationalConfernceonNeuralNetworks.Perth,Australia, 1995: 1941-1948. [8]ZahraB,SitiMHS,ShafaatunnurH.MPSO:Median-orientedParticleSwarmOptimization[J].AppliedMathematicsandComputation, 2013, 219(11): 5817-5836. [9]张学良,温淑花,李海楠,等. 基于Tent映射的混沌粒子群优化算法及其应用[J]. 中国机械工程,2008,19(17): 2108-2112. ZhangXuelang,WeiShuhua,LiHainan,etal.ChaoticParticleSwarmOptimizationAlgorithmBasedonTentMapping[J].Chinamechanicalengineering, 2008,19(17): 2108-2112.[10]IndranilP,AnnaK,SaptarshiD,etal.ChaosSuppressioninaFractionalOrderFinancialSystemUsingIntelligentRegroupingPSOBasedFractionalFuzzyControlPolicyinthePresenceofFractionalGaussianNoise[J].NonlinearDyn., 2012, 70 (4): 2445-2461.[11]张薇, 谢红梅, 王保平. 一种新型的分段logistic混沌扩频通信算法[J]. 计算机科学, 2013, 40(1): 59-62. ZhangWei,XieHongmei,WangBaopin.NovelPiecewiseLogisticChaoticSpreadSpectrumCommunicationAlgorithm[J].ComputerScience, 2013, 40(1): 59-62. [12]XuGang.AnAdaptiveParameterTuningofParticleSwarmOptimizationAlgorithm[J].AppliedMathematicsandComputation, 2013, 219: 4560-4569. (编辑王艳丽) Research on Mobile Robot FastSLAM Based on Chaos Optimization of MPSO Algorithm Zhu Qiguang1,2Xia Cuiping1Chen Weidong1,2Chen Ying1 1.Yanshan University,Qinhuangdao,Hebei,066004 2.The Key Laboratory for Special Fiber and Fiber Sensor of Hebei Province,Qinhuangdao,Hebei,066004 Aiming at the particle degradation problem of an mobile robot FastSLAM a chaos optimization MPSO based algorithm was proposed. The algorithm incorporated the newest observation information into the prediction of particle, adjusted the proposal distribution of the particles, and the accuracy of prediction of a robot’s position was enhanced. The MPSO was solved by a sequential two-step optimization strategy. Firstly, the speed of evolution of particle was improved by the median-oriented acceleration, the particle degradation effectively was overcome, the convergence of the algorithm was improved. Then, focusing on the depletion of the particle, the chaos search algorithm optimization algorithms was introduced to MPSO global optimal position to disperse gathered at local optimum particle swarm to the global optimum location close to broaden the scope of the solution space, thus maintaining the population the diversity of simulation. The experimental results prove that the improved method is correct and feasible. fast simultaneous location and mapping(FastSLAM); proposal distribution; media-oriented particle swarm optimization(MPSO); median-oriented acceleration; chaos 2014-01-15 国家自然科学基金资助项目(61201112,61172044);河北省自然科学基金资助项目(F2013203250, F2012203169);河北省普通高等学校青年拔尖人才计划资助项目(BJ2014056);燕山大学青年教师自主研究计划资助项目(14LGA013) TP183DOI:10.3969/j.issn.1004-132X.2015.05.004 朱奇光,男,1978年生。燕山大学信息科学与工程学院副教授。主要研究方向为机器人智能控制和多传感器信息融合及应用。发表论文30余篇。夏翠萍,女,1989年生。燕山大学信息科学与工程学院硕士研究生。陈卫东,男,1971年生。燕山大学信息科学与工程学院教授。陈颖,女,1980年生。燕山大学电气工程学院副教授。2 基于混沌MPSO的FastSLAM算法





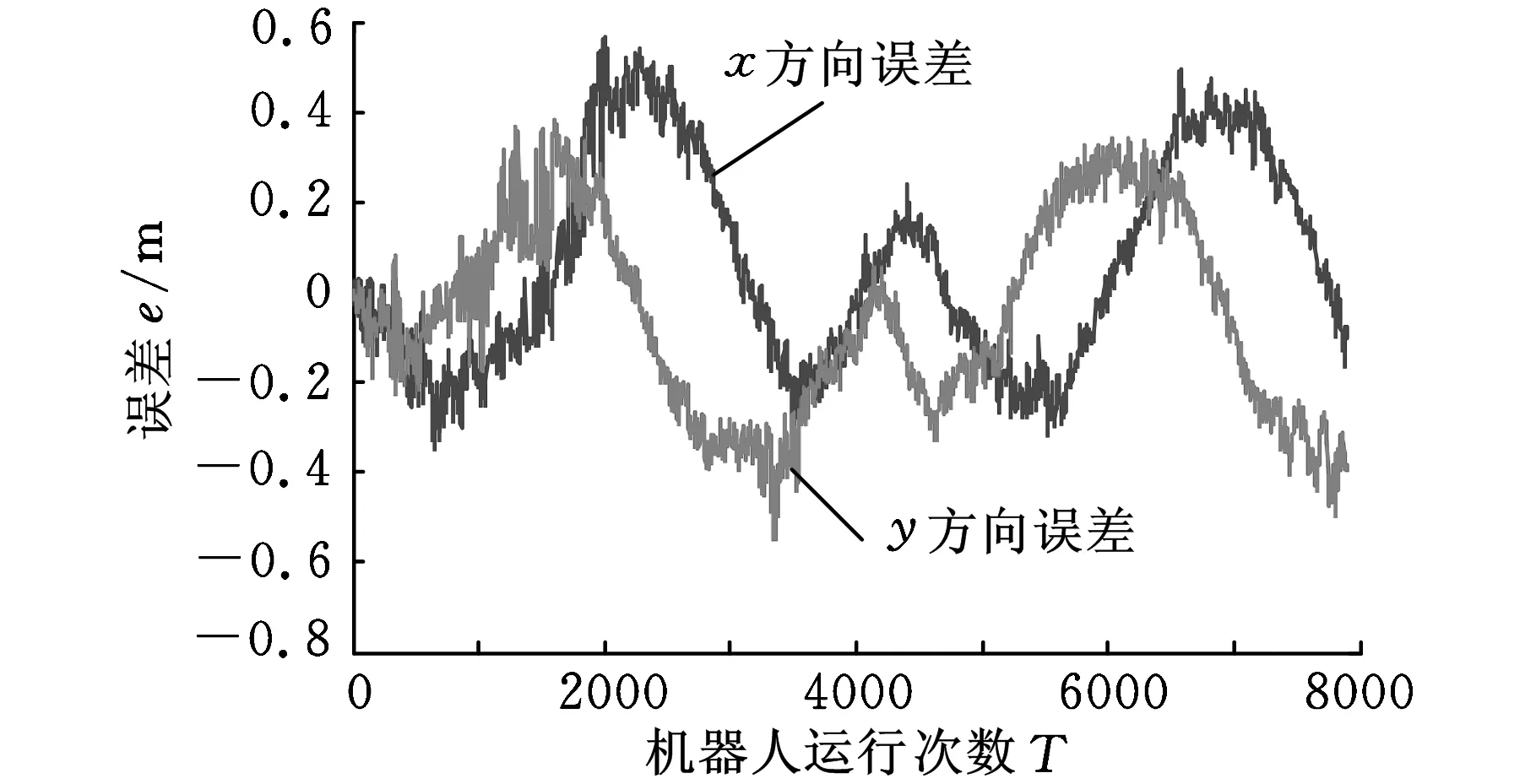
3 实验研究及其分析








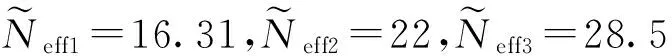
4 结论
