碟形砂轮加工刀具螺旋槽的磨削参数研究

曾　滔　周志雄　汤爱民　肖思来　左小陈

1.株洲钻石切削刀具股份有限公司，株洲，4120072.湖南大学，长沙，410082

碟形砂轮加工刀具螺旋槽的磨削参数研究

曾滔1周志雄2汤爱民1肖思来1左小陈1

1.株洲钻石切削刀具股份有限公司，株洲，4120072.湖南大学，长沙，410082

基于无瞬心包络原理，建立了刀具螺旋槽的数学模型，推导了螺旋槽磨削参数和设计参数之间的函数关系式；根据数学模型，利用MATLAB开发了用于计算螺旋槽磨削参数和数值仿真刀具槽形的人机交互式界面程序；将刀具仿真槽形与实际槽形进行对比，结果表明两者具有很好的一致性，这证明了数学模型的有效性。另外，初步讨论了设计参数与刀具磨削参数及槽形之间的变化关系。

螺旋槽；磨削参数；无瞬心包络；数学模型

0　引言

刀具是机械制造业的重要工具，在汽车、模具、航空航天、风电等典型行业发挥着重要作用。为了提高刀具的切削加工性能，一方面要开发出高性能的刀具基体和涂层材料，另一方面必须加强刀具结构设计理论和制造工艺的研究力度。对于整体硬质合金刀具来说，刀具的螺旋槽直接影响到刀具的排屑、容屑性能和刀具的几何参数、强度以及刚度等，设计并制造出良好的螺旋槽可以显著提高刀具的切削性能和使用寿命。

刀具螺旋槽的设计和成形理论研究领域中，正问题和反问题[1-2]是两个主要的研究方向。正问题，即给定砂轮轴截面形状求解螺旋槽横截面形状，如肖思来等[3]根据砂轮的数学模型，应用无瞬心包络原理，建立了一种深孔麻花钻的变参数螺旋槽的数学模型。反问题，即给定螺旋槽截面形状求解砂轮轴截面形状，如贾建军等[4]针对铣刀刃形的设计，采用神经网络方法建立了工件螺旋槽形与铣刀刃形之间的非线性关系模型，并通过工件螺旋槽端面截形模拟仿真出铣刀回转面刃形。不管是求解正问题还是反问题，其核心思想都是基于曲面共轭原理[5-7]，且砂轮的磨削参数已知。

然而，在刀具实际设计与加工过程中存在一类新问题亟待解决，这类问题即给定砂轮的轴截面形状，但不完全给定刀具螺旋槽横截面形状(一般用一组参数对螺旋槽截面形状进行限定)，求解砂轮的磨削参数，我们将其称为刀具螺旋槽加工中磨削参数的求解问题。与磨削参数求解问题紧密相关的一个严峻现实是，目前国内很多刀具制造厂家为了提高产品的生产能力和水平，大量引进国外先进的数控磨削加工中心，如WALTER、Rollomatic 620、ANCA等，然而，由于机床生产商对其核心技术实施严密封锁，使用者很难利用磨削中心进行CAM二次开发，而只能生产现有配套CAM软件中提供的若干种刀具，这不仅严重限制了设备的生产能力，而且不利于企业自主创新能力的提高。

目前，国内外针对磨削参数的求解问题进行深入研究的文献鲜见报道。因此，研究此类问题，突破国外在刀具三维设计和虚拟磨削仿真方面的技术壁垒，不仅有助于提高国内刀具的自主创新设计能力，而且能够为开发具有自主知识产权的整体刀具CAD/CAM集成系统提供理论基础。

1　螺旋槽设计参数和磨削参数

根据外形轮廓的不同，用来加工整体刀具螺旋槽的砂轮通常分为三种：平形砂轮、碟形砂轮和成型砂轮。平形和碟形砂轮因形状简单,设计操作方便,在实际工程中应用广泛。本文以碟形砂轮磨削刀具螺旋槽为例，对磨削参数的求解问题进行研究。

1.1螺旋槽设计参数

用碟形砂轮磨削刀具螺旋槽时，形成的螺旋槽分成两部分，前刀面A和反屑面B(以螺旋线m为界)，如图1所示。

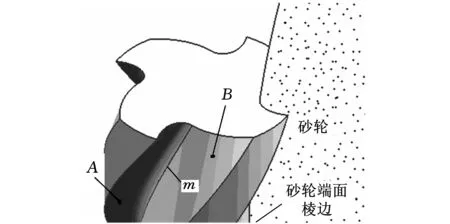
图1　碟形砂轮磨削刀具螺旋槽

图1中前刀面A是砂轮的大端面通过干涉法[8]磨削而成的，其本质是砂轮大端面的特征线[9]即由其端面棱边的螺旋运动形成；反屑面B由砂轮外圆周面特征线做无瞬心包络运动[3,10]形成。

在整体刀具的加工过程中，螺旋槽的加工是其重要的组成部分，螺旋槽的形状参数，尤其是螺旋刃前角、槽深、槽宽对刀具的切削过程有很大的影响。因此，设计刀具螺旋槽槽形时，一般通过螺旋刃前角γ、芯厚d0和端面刃瓣宽度ld三个参数限定容屑槽的几何形状，如图2所示。γ是端面上测量的刃尖(F点)到中心的连线与槽形曲线DEF在F点处的切线之间的夹角；d0是刀具螺旋槽的端截面轮廓的最大内切圆直径，其大小由前刀面A决定；ld是端面上测量的刀具刃瓣的宽度，可通过法向刃瓣宽度lf间接计算出来。

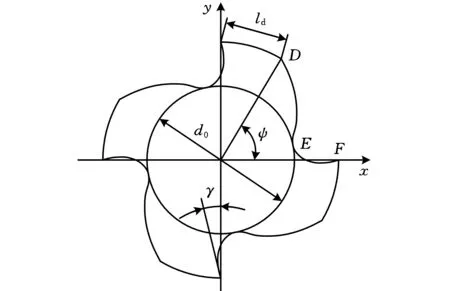
图2　刀具螺旋槽槽形设计参数

1.2螺旋槽磨削参数

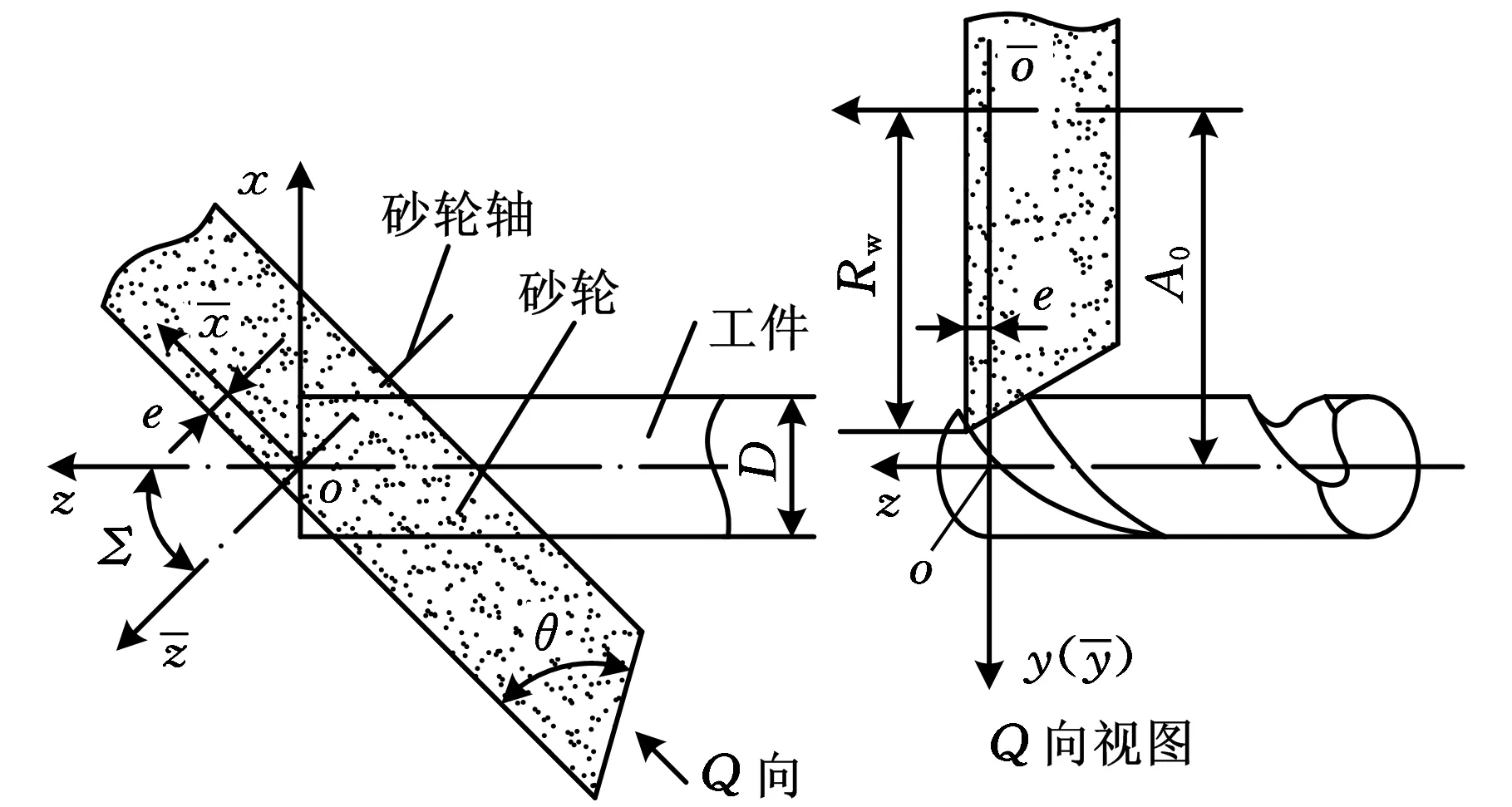
图3　刀具螺旋槽加工示意图

影响刀具螺旋槽的因素包括砂轮形状参数和磨削参数，通常在实际加工中，砂轮的形状参数是给定的，而磨削参数要根据螺旋槽的设计参数进行计算和调整。如图3所示，砂轮的形状参数包括半径Rw、锥度角θ和宽度，对于砂轮宽度，只要其值足够大且在加工过程中不发生干涉现象就不会影响螺旋槽形状，故文中不予考虑。

用来确定砂轮与刀具之间的相对空间位置关系的螺旋槽磨削参数有三个：轴间距A0、安装角Σ和端面偏距e(图3)。轴间距A0表示砂轮轴线与工件轴线之间的距离；安装角Σ表示两轴线之间的夹角；端面偏距e表示工件坐标系原点到砂轮左端面的距离。当给定螺旋槽设计参数后，就可根据螺旋槽加工的运动数学模型，得到磨削参数与设计参数之间的关系，进而求解出螺旋槽磨削参数。

2　螺旋槽的数学模型

2.1前刀面A的数学模型

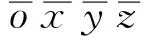
(1)

式中，λ为大端面棱边上任意点的相位角。

(2)

砂轮做螺旋运动对应的矩阵可表示为

(3)

式中，ε为螺旋运动参数，表示砂轮绕刀具轴线旋转的角度。

则在刀具坐标系oxyz中，螺旋槽前刀面A的方程表示为

(4)

将式(2)、式(3)代入式(4)得到螺旋面前刀面A的参数方程如下:

(5)

2.2反屑面B的数学模型

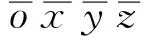
(6)

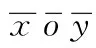
根据式(2)，在刀具坐标系oxyz中，砂轮外圆周面参数方程为

(7)

假设砂轮外圆周面上任意点的法向量为nw，根据上式求得

(8)

螺旋槽加工过程中，砂轮做螺旋运动，加工的每个瞬间，砂轮的空间位置不一样，不同位置的所有外砂轮圆周面形成一个曲面族。存在一个曲面与该曲面族中所有曲面都相切，该曲面即为曲面族的包络面，也就是螺旋槽反屑面B。故砂轮外圆周面与反屑面相切，该切线称为接触线，在接触线上的每一点上，砂轮外圆周面与螺旋面必有一条公法线，且公法线与砂轮轴线相交。

根据螺旋面特性方程[4]，有

ynx-xny=pnz

(9)

假设Q(x0,y0,z0)是接触线上的任意一点，由于螺旋面与砂轮外圆周面在该点处的法向共线，故Q点应同时满足式(7)和式(9)。将式(7)、式(8)代入式(9)并整理可得

(10)

令t=f(α)，则接触线的参数方程可表示为

(11)

根据式(11)和式(3)可得反屑面B的方程如下:

(12)

式中，σ为螺旋运动参数，表示砂轮绕刀具轴线旋转的角度。

3　设计参数与磨削参数的关系

3.1刀具螺旋刃前角与磨削参数的关系

根据螺旋槽前刀面A的方程式(式(5))，存在z=z0(此时λ=λ0，ε=ε0)的平面使得螺旋槽前刀面在该平面的截形曲线与刃径圆x2+y2=R2的交点为(R,0)，则

(13)

式(13)等价于

(14)

由式(14)求得λ0、ε0，则

z0=Rwcosλ0sinΣ+ecosΣ-pε0

(15)

当z=z0时，前刀面径向截形曲线方程为

(16)

其中ε表示成λ的函数如下:

(17)

根据式(16)、式(17)，当λ=λ0、ε=ε0时

(18)

刀具端截面螺旋刃前角的定义为

(19)

由式(18)、式(19)有

tanβsinΣsinλ0+cosλ0cosε0+tanγ=

(20)

3.2刀具芯厚与磨削参数的关系

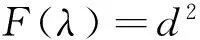
F(λ)=(RwcosλcosΣ-esinΣ)2+

(Rwsinλ-A0)2

(21)

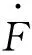
(22)

3.3端面刃瓣宽与磨削参数的关系

螺旋槽反屑面B在z=z0平面上的径向截形曲线与刃径圆x2+y2=R2交于D，假设刀具齿数为Nf，根据图2可求得

(23)

当z=z0时有

(24)

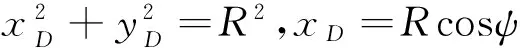
R2=(tsinα-A0)2+[tcosαcosΣ-

(ttanθ-Rwtanθ+e)sinΣ]2

(25)

Rcosψ=tcosαcosΣcosσ-[(t-Rw)tanθ+e]·

sinΣcosσ+(tsinα-A0)sinσ

(26)

至此，联立式(10)、式(14)、式(20)、式(22)、式(24)、式(25)和式(26)便可求解出螺旋槽磨削参数。

4　数学模型的验证

上述数学模型含有三个磨削参数，与工具磨床加工螺旋槽时采用三个参数定位砂轮是完全一致的。由于砂轮安装参数与刀具槽形具有唯一的对应关系，故本文通过对比刀具理论槽形与实际槽形，看二者是否一致，从而验证数学模型的有效性。4.1磨削参数的计算

由前文可知，求解螺旋槽磨削参数的非线性方程组由9个方程组成，且多数为超越方程，求解难度很大。MATLAB作为一款应用工具，处理数学问题的能力很强，特别是其中的fsolve命令，用其求解规模较大的非线性方程组的数值解非常方便。因此，本文利用该命令，在MATLAB中编写了一个可实现人机交互的GUI界面程序，该程序用来计算螺旋槽磨削参数，并能对碟形或平形砂轮磨削出的螺旋槽进行模拟仿真。

由于fsolve命令求方程数值解时采用的是迭代算法，求解过程和结果对迭代初值的依赖性很强，同时因求解磨削参数的方程组含有三角函数，其解通常存在多组，因此，迭代初值的选取非常重要，迭代初值选择不合适，很可能得不到正确解。编写GUI界面程序时，首先根据刀具加工的实际情况，确定磨削参数的合理范围和判定条件；然后在该范围内依次对不同的初值进行循环计算，并根据判别条件判断计算结果的正确性和合理性，从而决定循环是否终止，最终得到磨削参数的正确解。

下面用一个具体实例对上述GUI界面程序的功能进行演示。实例中刀具的结构设计参数如下：直径d=10mm，齿数Nf=4，螺旋角β=35°，螺旋刃前角γ=12°，芯厚d0=6.0mm，法向刃瓣宽lf=1.0mm。砂轮的形状参数为：锥度角θ=70°，半径Rw=75mm。磨削参数的计算结果及仿真出的槽形曲线如图4所示，图中显示：磨削参数中，端面偏距e=-1.21mm，安装角Σ=46.52°，轴间距A0=77.99mm。

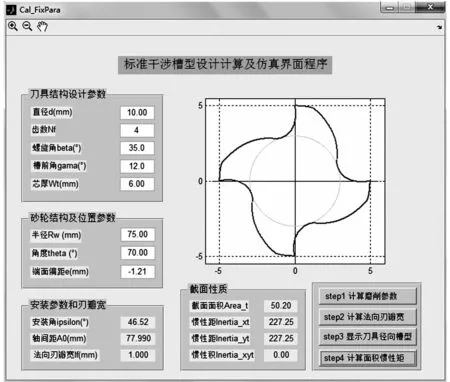
图4　刀具槽形设计计算及仿真实例

4.2理论槽形与实际槽形对比

根据表1中的三组刀具和砂轮参数，利用GUI界面程序对刀具槽形进行数值仿真，得到其理论槽形；另外，应用数控磨削中心加工出这三支刀具的螺旋槽，获取其径向截面槽形。

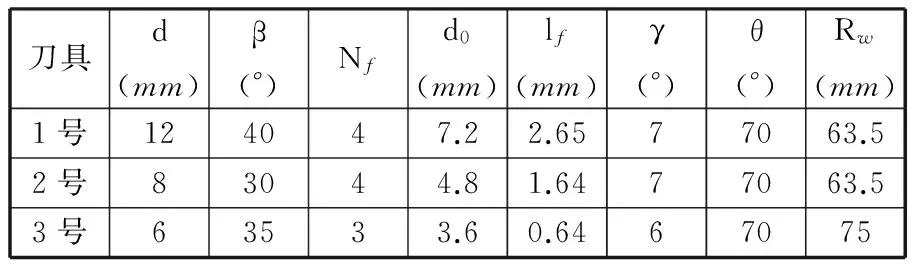
表1　槽形对比时采用的刀具及砂轮参数

图5所示为端截面上刀具理论槽形与实际槽形的对比情况。图中，三条圆弧的半径从小到大依次为3mm、4mm、6mm，很明显，刀具理论槽形与实际槽形几乎完全重合。在槽形曲线上沿D→E→F的顺序依次取25个近似等分点(图中黑点)，测量所有近似等分点处刀具理论槽形曲线与实际槽形曲线之间的法向距离，将其作为槽形误差，槽形误差分布曲线如图6所示。图中，误差正值表示理论槽形的深度比实际槽形深度大，其中1号、2号和3号刀具槽形最大误差依次为-36.2μm、-10.9μm和-11.7μm。由图5和图6的分析结果可见，刀具理论槽形与实际槽形具有很好的一致性，这证明了数学模型的有效性。

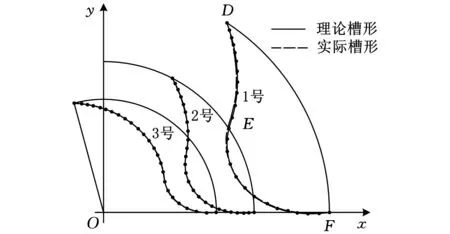
图5　刀具理论槽形与实际槽形对比

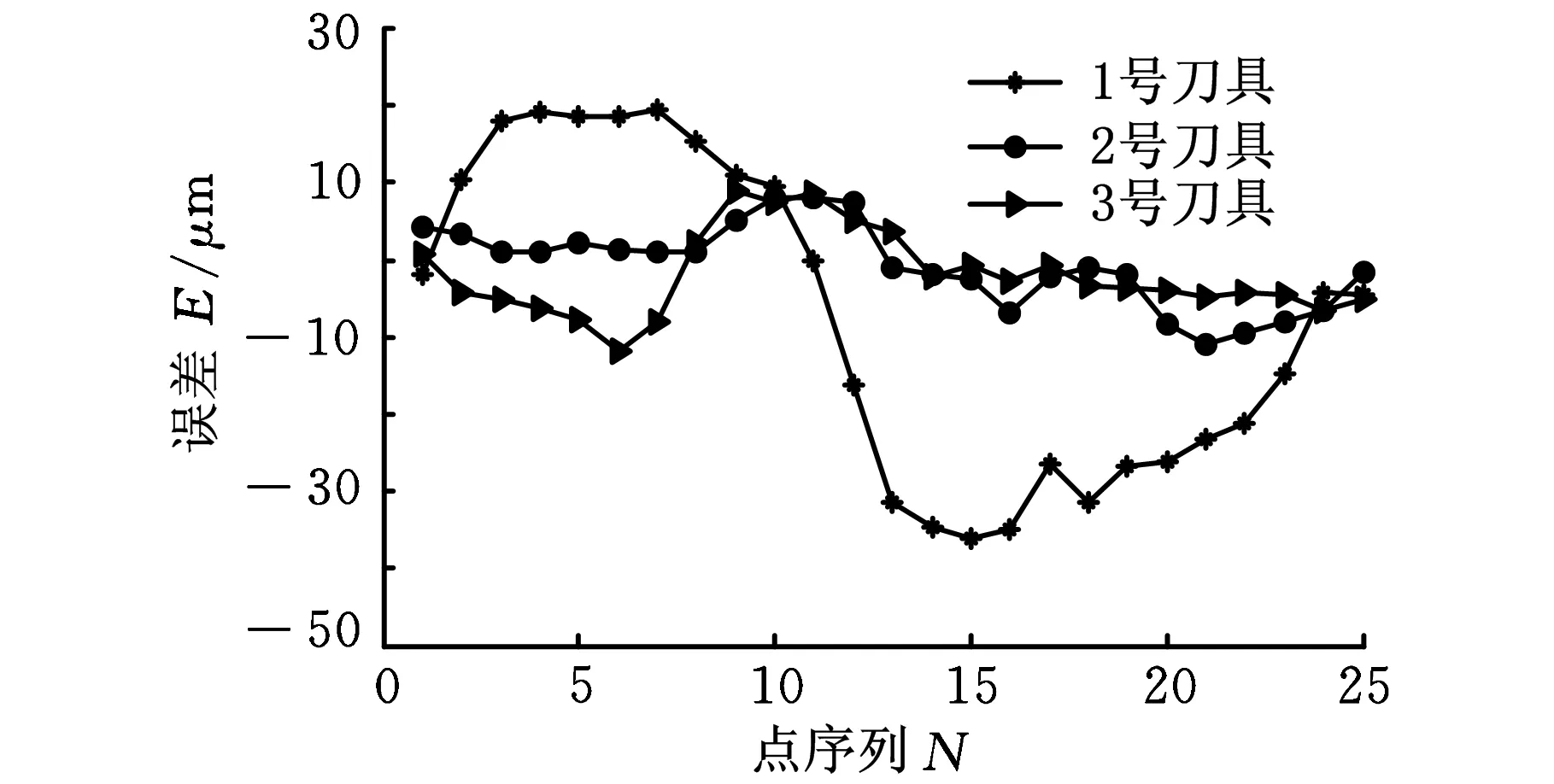
图6　槽形误差分布曲线

5　数值仿真分析

在不改变磨削砂轮形状参数(Rw=75mm、θ=70°)的条件下，分别单独改变刀具螺旋刃前角、芯厚和法向刃瓣宽，分析它们与磨削参数及刀具槽形之间的变化关系。

磨削参数的变化曲线如图7所示，据图7a，仅改变芯厚，砂轮端面偏距和安装角几乎呈现线性变化，而轴间距的变化曲线呈抛物线状；据图7b，仅改变法向刃瓣宽，砂轮端面偏距仍呈近似线性变化，安装角的变化很小，其最大最小值之差只有0.21°，轴间距的变化曲线仍呈抛物线状；据图7c，仅改变螺旋槽前角，砂轮端面偏距变化呈抛物线状，而安装角和轴间距近似呈线性变化。

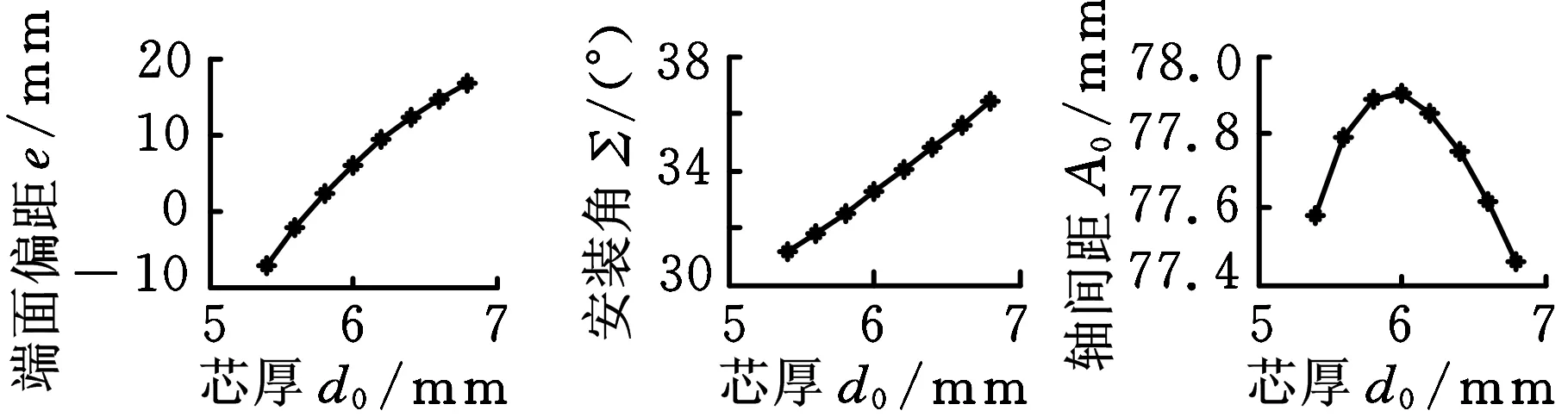
(a)芯厚与磨削参数的关系

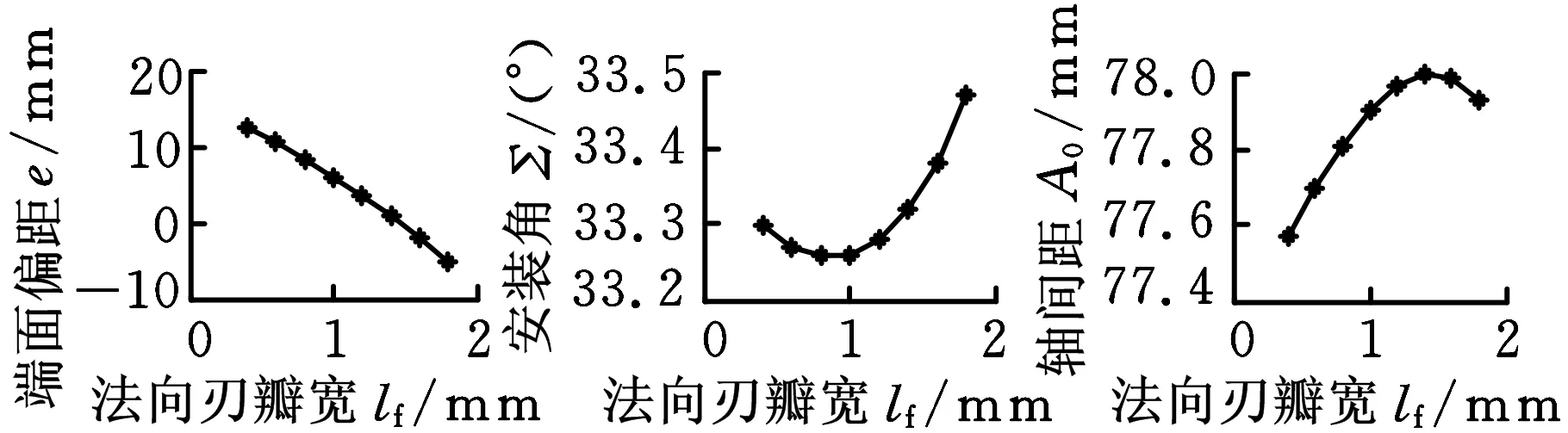
(b)法向刃瓣宽与磨削参数的关系

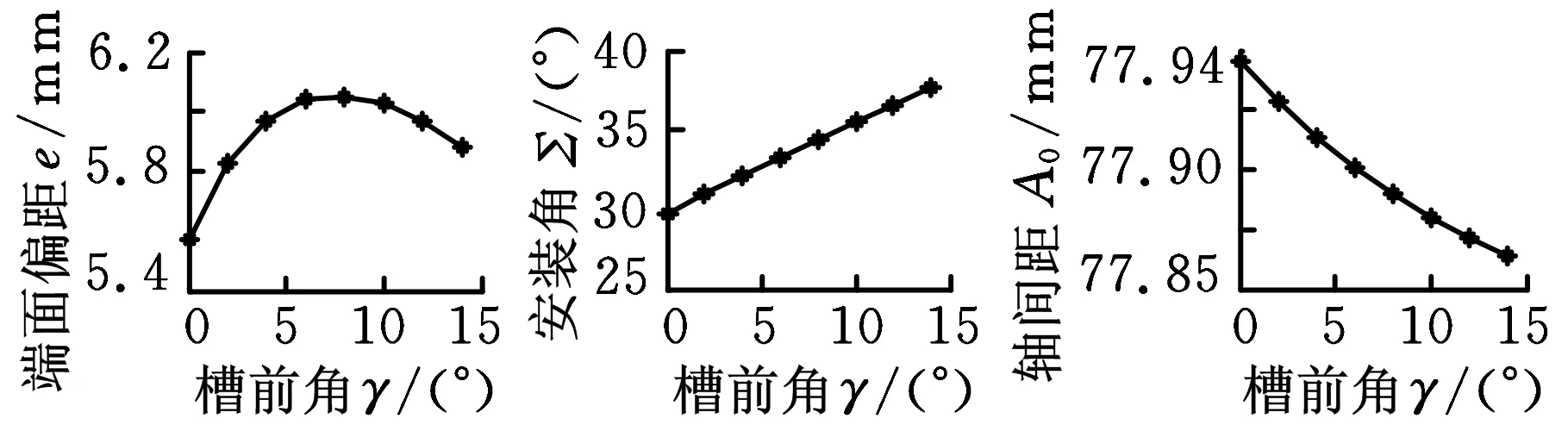
(c)槽前角与磨削参数的关系图7　螺旋槽磨削参数的变化曲线

表2中部分参数对应的刀具理论槽形如图8所示。由图8可见：芯厚的变化同时显著影响螺旋槽前刀面和反屑面，随着芯厚增大，刀具容屑空间显著减小；法向刃瓣宽的改变对反屑面的影响较大，而对前刀面几乎没有影响；螺旋刃前角的改变同时影响螺旋槽前刀面和反屑面，随着前角增大，前刀面内凹和反屑面外凸程度加深，但刀具容屑空间变化很小。

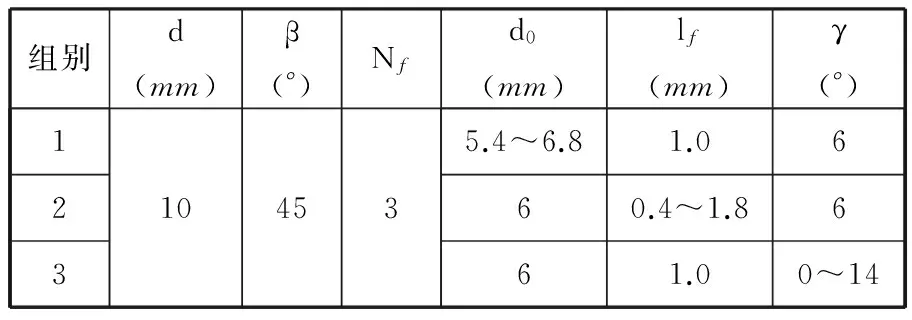
表2　刀具结构和设计参数

6　结论

(1)提出了刀具螺旋槽磨削加工中磨削参数的求解问题的概念，建立了应用标准碟形砂轮磨削的刀具螺旋槽的数学模型，推导了螺旋槽磨削参数和设计参数之间的函数关系式，为求解螺旋槽磨削参数、仿真刀具槽形提供了理论基础。

(2)利用MATLAB开发了用于计算磨削参数和仿真刀具槽形的人机交互式界面程序，通过该程序计算出的理论槽形与实际槽形的对比结果证明了数学模型的有效性。

(3)磨削参数变化曲线表明：虽然磨削参数与设计参数之间存在复杂的非线性关系，但在合理的范围内，可以用线性或二次函数对其进行拟合。

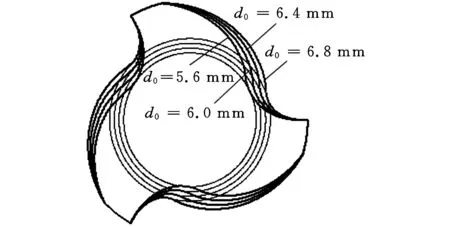
(a)改变芯厚(d0分别为5.6、6.0、6.4、6.8 mm)

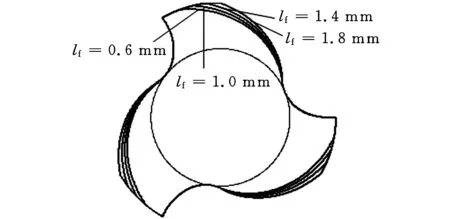
(b)改变法向刃瓣宽(lf分别为0.6、1.0、1.4、1.8 mm)

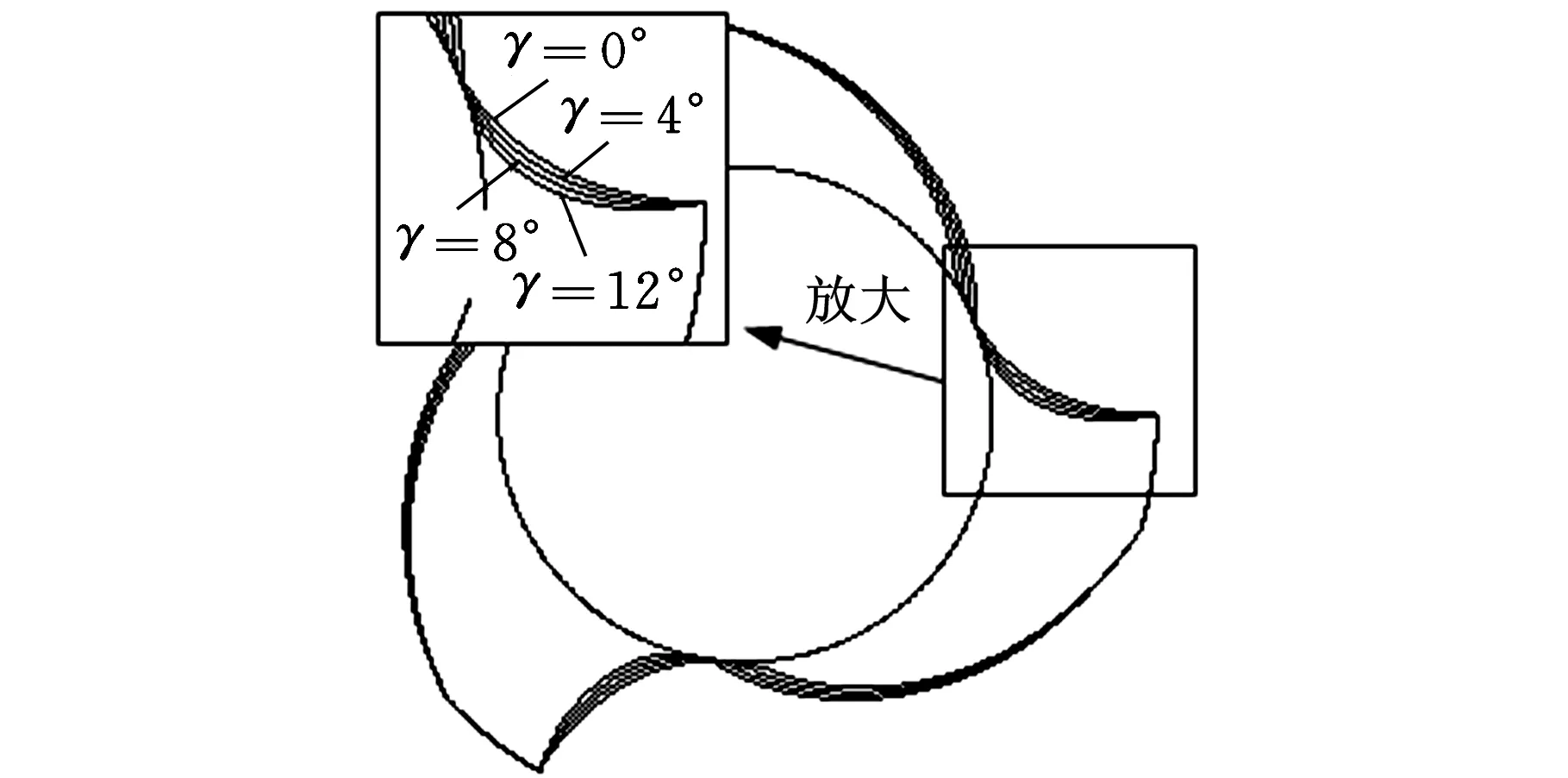
(c)改变螺旋刃前角(γ分别为0°、4°、8°、12°)图8　不同设计参数下刀具槽形的差异

[1]KangSK，EhmannKF，LinC.ACADApproachtoHelicalGrooveMachining—Ⅰ.MathematicalModelandModelSolution[J].InternationalJournalofMachineTools&Manufacturing，1996，36(1)：141-153.[2]HsiehJ.MathematicalModelandSensitivityAnalysisforHelicalGrooveMachining[J].InternationalJournalofMachineTools&Manufacturing，2006，46：1087-1096.

[3]肖思来，周志雄，左小陈，等.深孔麻花钻变参数螺旋槽的数字建模研究[J].中国机械工程，2011，23(21)：2555-2559.

XiaoSilai，ZhouZhixiong，ZuoXiaochen，etal.StudyonDigitalModelingofSpiralGrooveswithVariableParametersforDeepHoleTwistDrills[J].ChinaMechanicalEngineering，2011，23(21)：2555-2559.

[4]贾建军，王建华.神经网络在加工螺旋面中的应用研究[J].中国机械工程，2008，19(16)：1935-1938.

JiaJianjun，WangJianhua.ApplicationResearchofNNintheHelicalGrooveMachining[J].ChinaMechanicalEngineering，2008，19(16)：1935-1938.

[5]姚南殉.异型螺旋曲面数控加工运动学研究与应用[J].机械工程学报，2004，40(6)：113-117.

YaoNanxun.StudyontheKinematicsofNCMachiningfortheHelicoidwithSpecialSpaceandItsApplication[J].JournalofMechanicalEngineering，2004，40(6)：113-117.[6]汪国平，华宣积，孙家广.复杂螺旋曲面铣削加工的几何特性分析[J].清华大学学报，2000，40(9)：49-52.WangGuoping，HuaXuanji，SunJiaguang.GeometricCharacteristicAnalysisoftheMillingofHelicoids[J].JournalofTsinghuaUniversity(Science&Technology)，2000，40(9)：49-52.

[7]潘秀英，潘维海.强力磨削螺旋形刃沟的砂轮截形计算[J].哈尔滨理工大学学报，1998，3(2)：13-16.

PanXiuying，PanWeihai.CalculationofWheelSectionFormofSpiralFluteFormedbyPowerfulGrinding[J].JournalofHarbinUniversityofScienceandTechnology，1998，3(2)：13-16.

[8]毛世民，聂钢，吴序堂.前角可控的等螺旋角锥形铣刀三轴数控加工原理[J].西安交通大学学报，1999，33(7)：79-83.

MaoShimin，NieGang，WuXutang.ThreeAxesNumericalControlMachiningofTapeMillCutterwithEqualHelicalAngleandControllableRakeAngle[J].JournalofXi’anJiaotongUniversity，1999，33(7)：79-83.

[9]黄波，罗学科.应用标准砂轮加工刀具螺旋槽的特征线研究[J].组合机床与自动化加工技术，2006(1)：12-15.HuangBo，LuoXueke.StudyonCutterFluteProducedbyStandardGrindingWheelthroughCharacteristicLineMethod[J].ModularMachineTool&AutomaticManufacturingTechnique，2006(1)：12-15.[10]钟罗杰，陈益瑞，关彪.一种由铣刀刃形求螺旋槽形状方法的探讨[J].湛江海洋大学学报，2001，21(4)：59-62.

ZhongLuojie，ChenYirui，GuanBiao.AMethodforCalculatingHelicalGroovefromtheShapeofMilling-cutterEdge[J].JournalofZhenjiangOceanUniversity，2001，21(4)：59-62.

(编辑王艳丽)

Research on Grinding Parameters in Machining Helical Groove of Cutting Tools with a Dishing Wheel

Zeng Tao1Zhou Zhixiong2Tang Aimin1Xiao Silai1Zuo Xiaochen1

1.Zhuzhou Cemented Carbide Cutting Tool Co.,Ltd.,Zhuzhou,Hunan,412007 2.Hunan University,Changsha,410082

Based on the theory of non-instantaneous center enveloping, a mathematical model of helical groove was established, and the function of grinding parameters and design parameters were deduced. According to the mathematical model, a human-computer interactive interface used to calculate the grinding parameters and simulate the groove section was developed, and then the section profile of the simulative groove and actual groove were compared. The results show a good agreement and verify the validity of the mathematical model. In addition, variations of grinding parameters and groove influenced by design parameters were simply discussed.

helical groove; grinding parameter; non-instantaneous center enveloping; mathematical model

2013-12-11

国家科技重大专项(2013ZX04005-021)；湖南省科技计划资助项目(2013WK2020)

TG701< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.05.002

曾滔，男，1982年生。株洲钻石切削刀具股份有限公司研发中心设计部工程师。主要研究方向为刀具的三维建模以及整体刀具结构设计与开发。周志雄，男，1953年生。湖南大学机械与运载工程学院教授、博士研究生导师。汤爱民，男，1969年生。株洲钻石切削刀具股份有限公司技术总监、博士、高级工程师。肖思来，男，1969年生。株洲钻石切削刀具股份有限公司总经理助理、博士、高级工程师。左小陈，男，1981年生。株洲钻石切削刀具股份有限公司刀具一厂副厂长。