基于圆台形热传导模型的慢走丝线切割仿真与试验

王　艳　杨　林　丁成才　丁成业

1.上海理工大学，上海，200093　　2.泰州市江洲数控机床制造有限公司，泰州，2253003.南京交通职业技术学院，南京，210000

基于圆台形热传导模型的慢走丝线切割仿真与试验

王艳1杨林1丁成才2丁成业3

1.上海理工大学，上海，2000932.泰州市江洲数控机床制造有限公司，泰州，2253003.南京交通职业技术学院，南京，210000

基于放电通道中等离子体的形成机理，根据慢走丝线切割在短脉冲放电加工时放电通道中电子流与离子流散射速度的差异，提出了圆台形热传导模型。采用基于圆台形热传导模型的有限单元法对航空材料Inconel718的典型工况进行了仿真计算，系统地分析了放电能量对放电通道温度以及放电蚀坑深度的影响规律，并采用声发射检测技术在线监测慢走丝线切割的加工表面粗糙度。通过仿真结果与试验测得工件表面粗糙度Rt值的对比，再结合试验测得的声发射信号波形图特征及声发射信号均方根值发现：仿真计算得到的放电蚀坑深度与表面粗糙度Rt值吻合较好；声发射信号的强度随着放电能量的增加而增强，声发射信号强度随着放电温度变化速率的变小而减弱。最后回归分析得到材料表面粗糙度与声发射信号均方根值的数学预测模型，预测结果与测得的表面粗糙度误差仅为4.4%。

Inconel718；线切割；圆台形热传导模型；有限元；声发射；回归分析

0　引言

航空材料Inconel 718具有优良的高温蠕变强化性能、抗疲劳性能以及抗氧化和抗热腐蚀性能，并且能在高温下承受高应力、保持较好的机械和化学性能，所以被广泛应用于涡轮机叶片、液体燃料火箭以及飞机发动机等组件的制造[1]。传统切削加工方法(磨削、切削)加工Inconel 718时，材料塑形变形大，切削力高，热效应影响大，刀具磨损严重，而且刀具上易形成积屑瘤从而降低加工表面的质量[2]，是典型的难加工材料。 慢走丝线切割加工是靠放电产生高温使材料熔化、气化，并在压力电介质的作用下去除材料，无需考虑材料的力学性能，非常适合加工传统切削方法难以加工的导电材料。

慢走丝线切割加工脉冲时间短、切缝窄且温度极高，常规检测设备难以直接测量其温度。数值模拟方法已成为研究放电通道内温度场的一种有效方法，通过分析温度分布还可估算放电蚀坑的深度。慢走丝线切割加工过程非常复杂，数值模拟时需要作适当的简化，文献[3-5]在仿真分析时都将等离子体简化为圆柱形，本文则基于放电通道中等离子体的形成机理，提出了圆台形热传导模型。 目前对数值模拟准确性验证的方法不多，应用动态检测方法对放电加工过程数值模拟进行验证的方法较少。声发射检测对声发射传感器与被测工件的接近程度要求不高，若检测时使用采样频率足够高的采集卡则能同时克服高温[6-7]、空间狭小等多个难题。

国内外对声发射技术在电火花加工中的应用进行了研究。El-Menshawy等[8]通过区分火花放电与电弧放电时声发射信号特征来监测极间的放电状态，但未能排除环境噪声的影响；陈湛清等[9]研究了不同脉冲参数条件下不同放电状态时可闻声部分的声特征；Craig等[10]应用声发射信号确定电火花线切割加工时放电点的空间位置；Muslim等[11]研究了声发射信号特征与放电能量的关系，并根据声发射信号特征探测了电火花加工中的破裂现象。上述研究表明，火花放电与电弧放电具有截然不同的声发射信号特征：火花放电时声发射信号不仅强度大，而且有特殊频率；而电弧放电时的声发射信号强度非常弱，因此可以用声发射信号的特征来监测极间的放电状态。但以上研究过程中都未能完全排除加工过程中噪声信号的影响，而且声音信号具有一定的滞后性，采用声信号监测极间放电状态并不如根据电压的变化特征来监测极间放电状态响应快[12]。

本文首先基于等离子体中电子流与离子流的运动特性，提出更接近放电通道位形的圆台形热传导模型，采用基于圆台形热传导模型的有限单元法对Inconel 718在不同放电能量下的温度场进行分析计算，再进行应用声发射技术监测慢走丝线切割试验，对比分析了理论蚀除量和实际蚀除量以及与试验采集到的声发射信号之间的对应关系，建立了采用声发射信号均方根值预测工件表面粗糙度的数学模型，为慢走丝线切割加工表面粗糙度的在线监测提供了一种切实可行的方法。

1　圆台形热传导模型的建立

慢走丝线切割是一种高度复杂的特种加工工艺，仿真时考虑所有的影响因素并不现实，将其简化为热效应为主导的加工过程产生的误差较小。而在对以热效应为主导的加工过程进行分析时，首先需要建立放电热传导模型，需要明确定义以下三个要素：能量分配系数，热传导模型及材料的去除准则。

1.1极间放电能量分配系数

慢走丝线切割加工的热量分配如下(图1)：

Qz=Qy+Qf+Qj

(1)

式中，Qz为放电过程产生的总能量；Qy为工作液对流带走的能量；Qf为热辐射消耗的能量；Qj为传入工件和电极丝的能量。

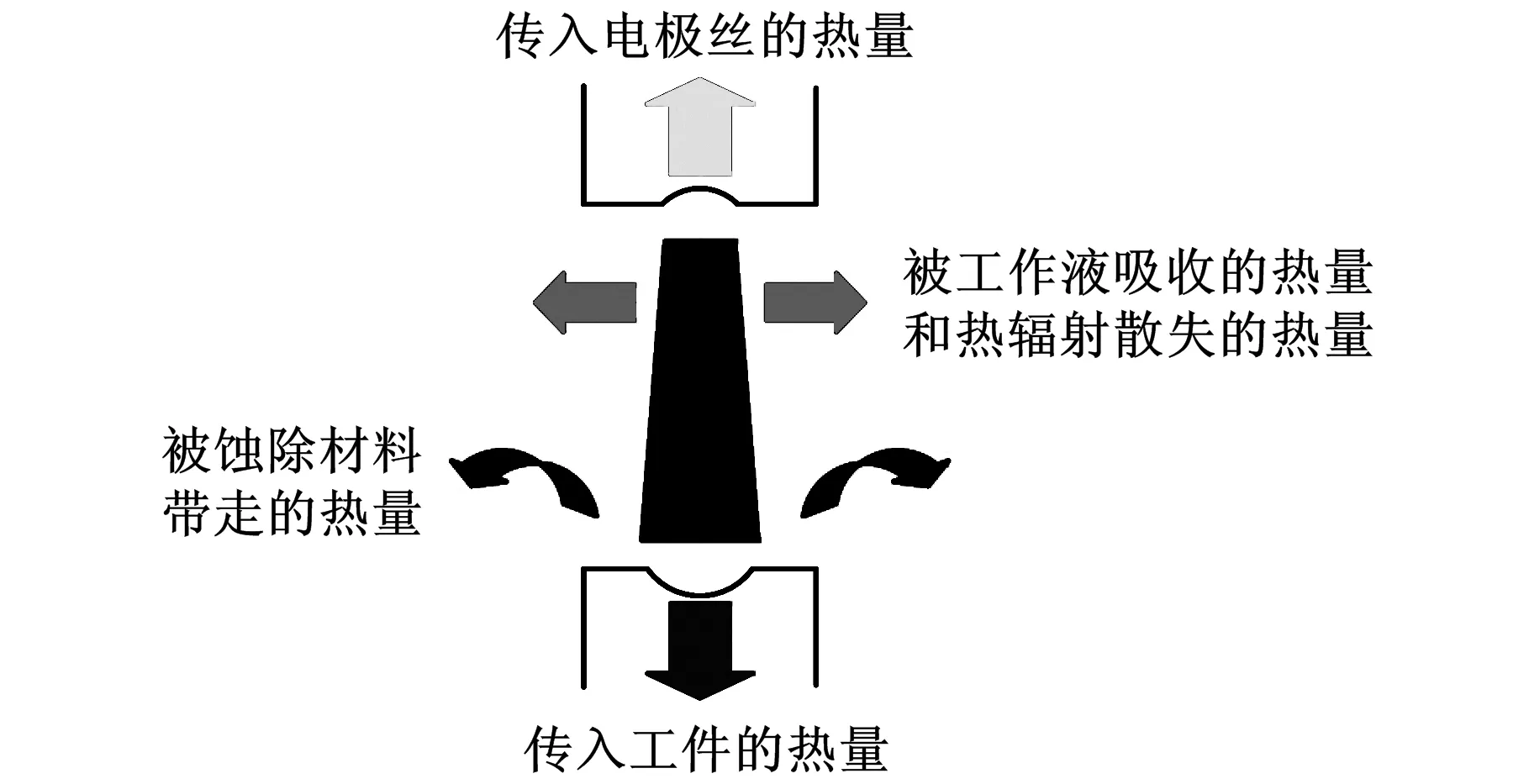
图1　能量分配图

学者们对放电能量在电极丝与工件间的分配关系进行了大量的研究。Eubank等[3]认为传入电极的能量百分比是常数，理论计算与试验检测结果都表明阳极和阴极吸收热能的比例为2∶1。Xia等[4]认为能量分配与脉冲宽度无关，分配到阳极和阴极的能量比例分别为40%和20%，本文也采用此能量分配系数。

1.2圆台形热传导模型

慢走丝线切割放电加工过程中，工作液被击穿形成放电通道，如图2所示。通道中的电子和正离子在电场的加速作用下高速运动时会发生剧烈碰撞，碰撞产生大量的热，同时高速带电粒子轰击电极表面将自身的动能转化为热能，迅速加热电极表面。

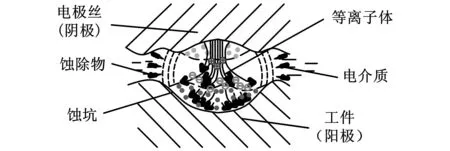
图2　放电通道示意图

放电通道的位形即模型的大小和形状，是研究放电通道热传导模型需要考虑的最主要因素。有些文献在仿真分析时都假设热传导模型为圆柱形，但都忽略了粒子之间的碰撞。放电通道中的粒子碰撞不仅是不可避免的，而且还十分剧烈，并会引起放电通道的位形扩散。在放电通道的各种碰撞中，对其位形扩散有影响的主要是带电粒子之间的碰撞。不同粒子的扩散系数可用下式表示[13]：

(2)

式中，D为扩散系数；v为不同粒子的运动速度；υ为碰撞频率。

电子的质量远小于正离子的质量，电子在加速电场作用下获得更高的运动速度，而通道中电子和正离子的数量是相等的，因此它们的碰撞频率也相同，则根据式(2)可知电子流的扩散系数是离子流扩散系数的(ve/vp)2倍(ve是电子的速度，vp是离子的速度)。因为脉冲时间内放电通道中的电子流扩散集中在阳极附近，离子流扩散集中在阴极附近，所以使得平衡时放电通道呈现图3所示的喇叭形。

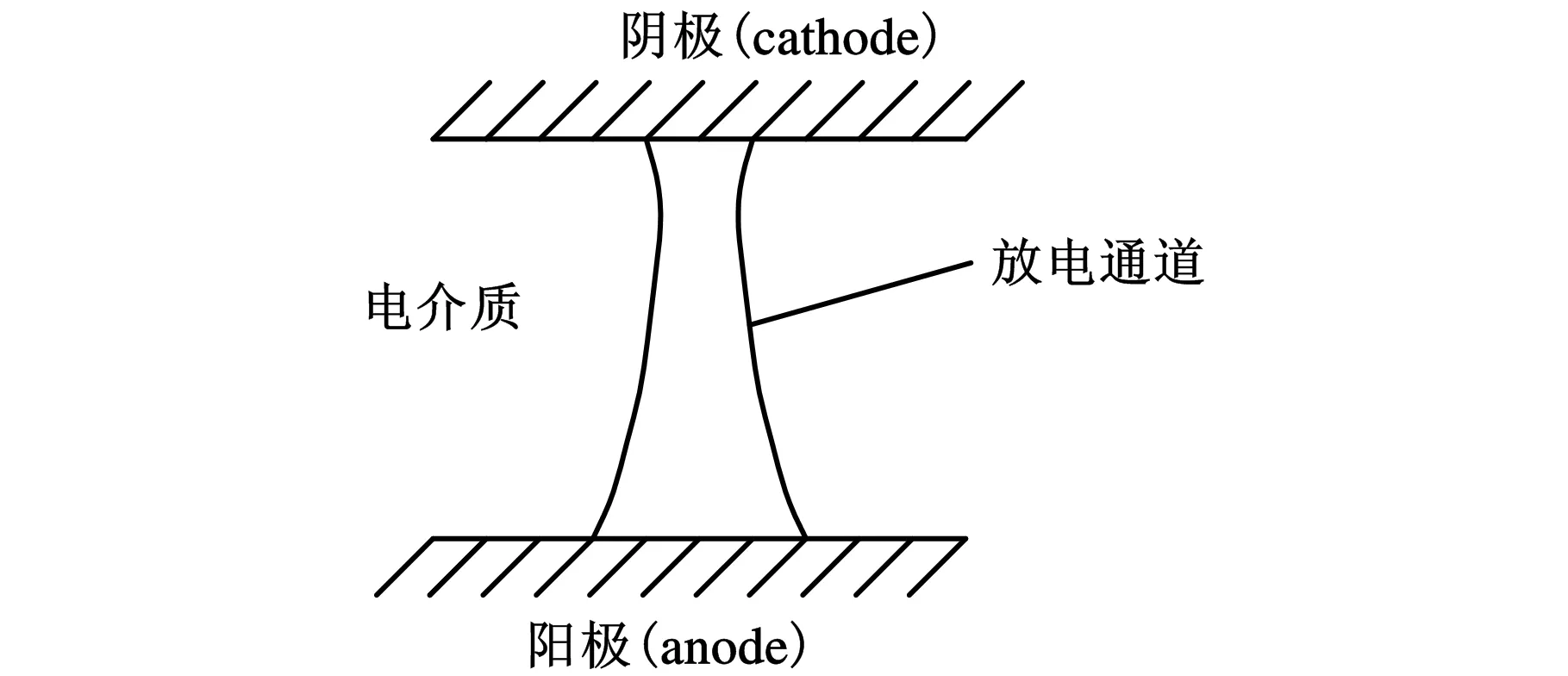
图3　放电通道平衡状态的位形

Perez等[14]用如下所示指数函数确定热传导模型半径：

RM(t)=Rptn

(3)

式中，RM为模型半径;Rp、n为系数;t为脉冲宽度。

Perez等给出了阴极的放电通道半径公式中参数的最佳值，n=0.2，Rp=251μm/s0.2。

因此根据平衡时放电通道位形的特点，将放电通道简化成图4所示的圆台形。阴极附近的放电通道半径可按式(3)计算：

Rc=RM

(4)

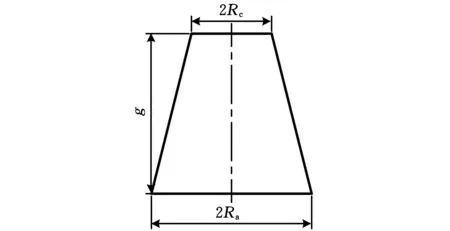
图4　放电通道纵截面

而慢走丝线切割加工过程中工件作为阳极，因此需要确定阳极附近的放电通道半径。根据阴极和阳极的放电能量分配系数，并假设放电通道内任意横截面上的热流密度分布函数相同，则阳极放电通道半径Ra满足下式：

(5)

式中，Aa、Ac分别为阳极和阴极附近的放电通道横截面积；q为放电通道内的热流密度。

Descoeudres等[15]使用光谱技术进行研究，发现放电通道内的热流密度近似遵循高斯分布，如图5所示。若放电通道轴向最大热流密度q0与通道半径R已知，那么距通道轴线为r处的热流密度q(r)为

(6)

假定一个脉冲只产生一次火花放电，则上式可改为

(7)

式中，U为放电电压(V)；I为放电电流(A)；Rw为工件上的能量分配系数；R为放电通道半径(m)。

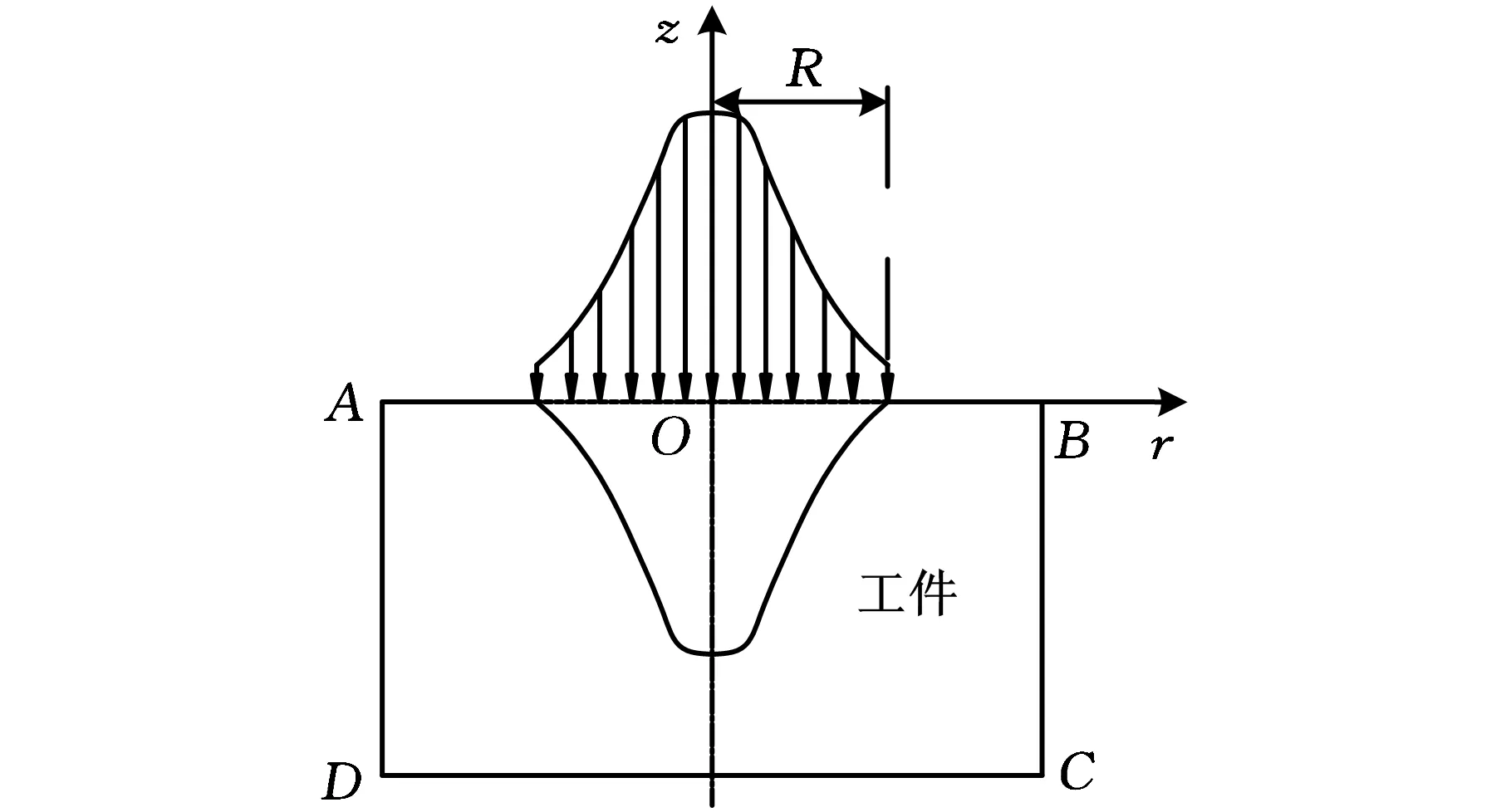
图5　高斯热源模型

1.3材料的去除准则

关于放电加工过程中材料的去除准则，有些学者认为熔化和气化的材料全部被去除，另有学者提出了过热理论，即在脉冲宽度时间内，处于放电通道区域内的材料温度被加热到超过材料沸点时，等离子体的高压阻止了材料气化。当脉冲结束时高压消失，过热的金属凹坑内发生微爆炸蚀除了一部分熔化的金属。Izquierdo等[6]用当量温度Teq来衡量材料是否被去除，即工件材料温度高于当量温度的部分被去除。本文采用高于工件材料熔点的材料都被去除的准则。

2　基于圆台形热传导模型的仿真分析

2.1有限元分析模型

在慢走丝线切割加工过程中，电极丝单次利用，故电极丝的损耗对加工精度的影响较小，Han等[16]研究的对象是电极丝，而本文的研究对象为工件，因此需基于圆台形热传导模型对文献中的分析模型稍加改进，如图6所示。

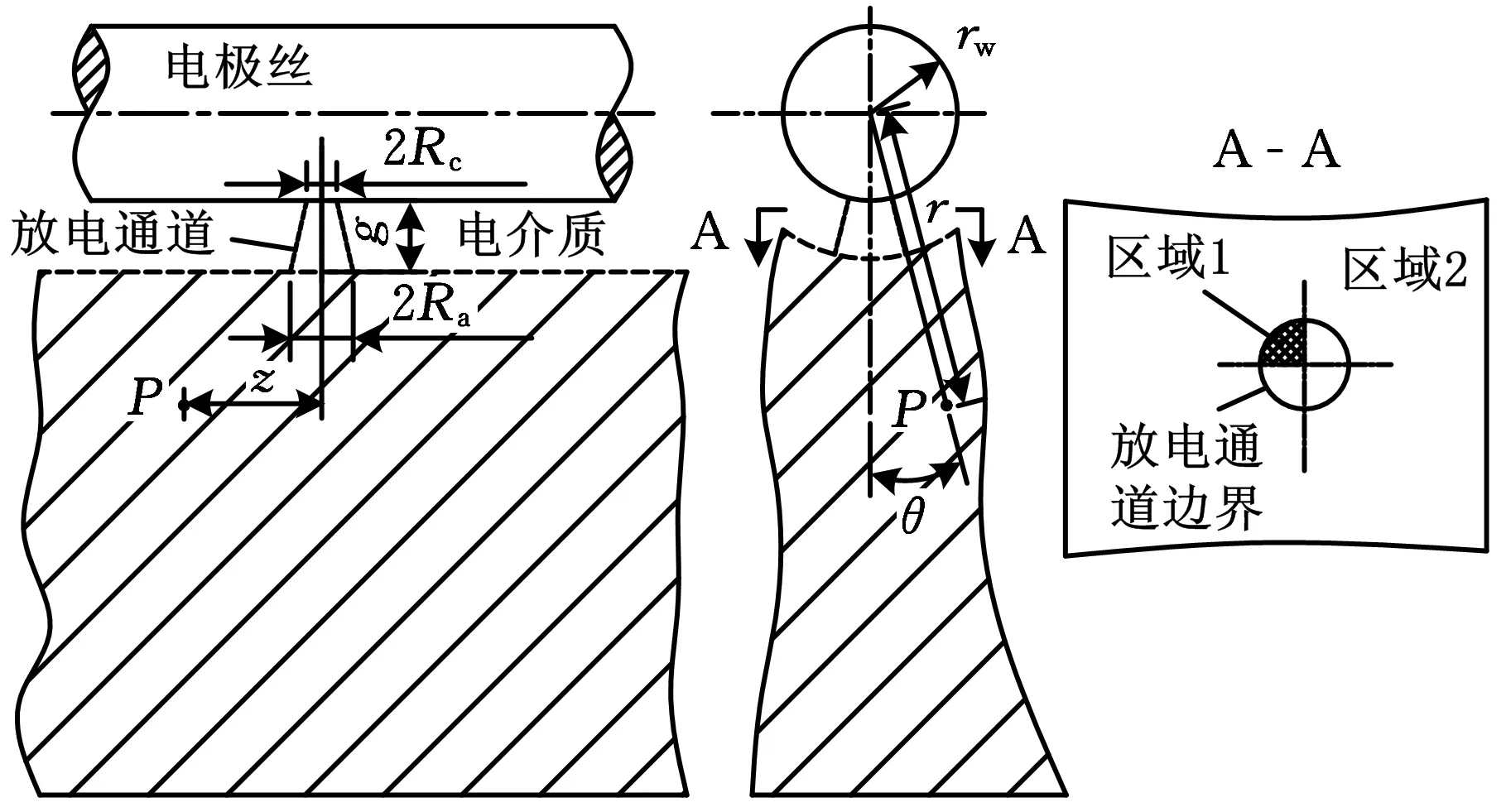
图6　热分析模型

对于工件上任意一个微单元体，其几何中心位于P点，以电极丝轴线方向为z轴，以放电点z轴的坐标位置为零，建立以电极丝中心线为z轴的圆柱坐标系，从而得到导热微分方程如下：

(8)

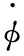
如图6所示，工件外表面被放电通道划分成两个区域：放电通道内部与外部。这两个区域内不同的对流换热构成了电极丝与工件传热问题的边界条件。在工件上：区域1与区域2的边界线可根据以下方程进行求解：

(9)

式中，g为放电间隙；rw为电极丝半径。

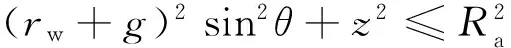
(10)

式中，qm为传入单位体积内单元体的热量。

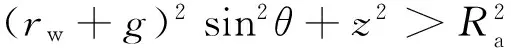
(11)

2.2仿真结果分析

在如此复杂的边界条件下求解上述微分方程几乎是不可能的，本文采用目前较常用且可靠的有限元软件ANSYS进行慢走丝线切割的热分析，仿真时做了如下假设：①认为工作区域是周对称的；②所用工件材料是均匀的、各向同性的；③忽略潜能的影响，因为它对仿真结果的影响可以忽略不计；④热能通过热传导的形式传入工件；⑤决定材料被去除的标准是临界温度Teq，温度高于这个值的材料都认为被去除；⑥电流和电压在脉冲时间内是常数；⑦不考虑电弧和短路的影响；⑧不考虑放电通道发生跳跃的影响，即便它可能会影响材料的表面性能。

建模时，选取直径为3 mm、高为1.5 mm的圆柱形进行建模。根据对称性，可以选择通过圆柱体轴线的纵截面的一半建立平面有限元模型，即将模型简化为边长为1.5 mm的正方形。在慢走丝线切割放电过程中，放电通道内工件的温度的变化范围大且速率快，所以仿真时需输入随温度不断变化的各物性参数的离散数值，系统会根据已输入的离散数值进行线性插值。Inconel 718随温度变化的物理性能参数如表1所示。

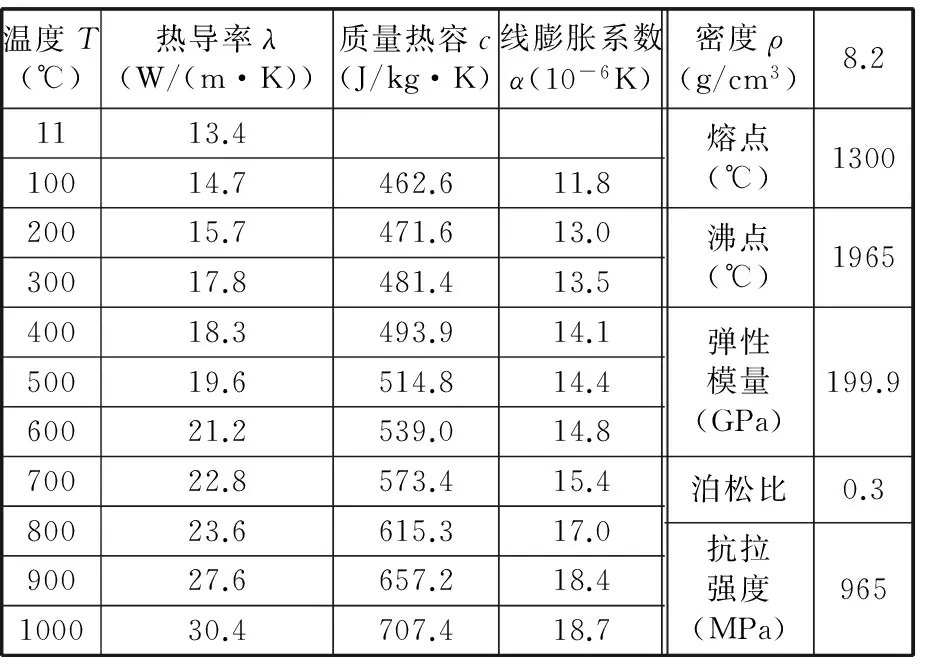
表1　Inconel718物理性能参数

根据Cheng等[17]的研究，放电通道半径内外对流传热系数并不相同，如表2所示。表3为计算热流密度时所需要的参数，与试验所设置的参数相同。加载时在工件表面放电通道内同时施加热流密度和热对流载荷，而在放电通道外只施加热对流载荷，仿真结果如图7～图10所示。

表2　不同位置对流传热系数

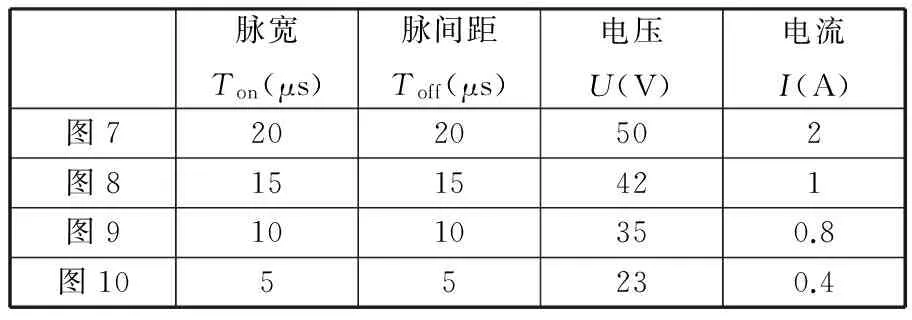
表3　仿真参数

图7　Ton=20 μs温度分布图

图8　Ton=15 μs温度分布图

图9　Ton=10 μs温度分布图

图10　Ton=5 μs温度分布图

由图7可知，在脉宽为20 μs时，符合材料去除准则的材料温度大都超过Inconel 718的沸点，说明Inconel 718主要是气化被去除。而由图8～图10可知，在脉冲宽度为5～15 μs时，符合材料去除准则的材料温度大都在沸点以下，因此20 μs可作为Inconel 718是气化还是熔化去除为主的临界值。

由图7～图10可知，在ANSYS中可测出脉宽从20 μs到5 μs下对应仿真蚀坑的深度分别为14.50 μm、9.85 μm、8.82 μm和4.38 μm，且从温度云图的形状可以看出放电蚀坑呈椭圆形，即蚀坑的深径比较小。放电蚀坑相互交错重叠就形成了工件的表面形貌，因此放电蚀坑大小与工件的表面粗糙度具有一定的对应关系。

各参数条件下仿真的最高温度如图11所示，可知放电通道最高温度从脉宽20 μs到15 μs急剧降低，而脉宽从15 μs到5 μs最高温度的降低变缓，说明慢走丝线切割加工过程中，放电通道的最高温度随放电能量的变小而降低。

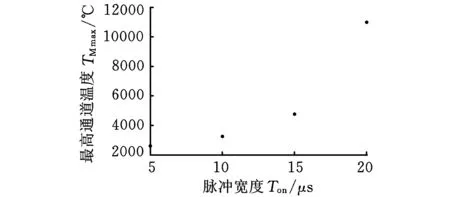
图11　最高温度散点图

图12是脉宽为20 μs时放电通道最高温度随时间的变化曲线。通道温度在开始时上升速度快，随后速度减慢，在脉冲时间结束时达到最高值。而温度的变化对应着放电能量的变化，通过该曲线可以得出放电加工过程中放电能量的变化规律。本文通过分析慢走丝线切割加工过程的放电能量变化规律与试验采集到的声发射信号特征之间的相互关系，为根据声发射信号均方根值在线监测慢走丝线切割加工工件的表面粗糙度提供了理论依据。

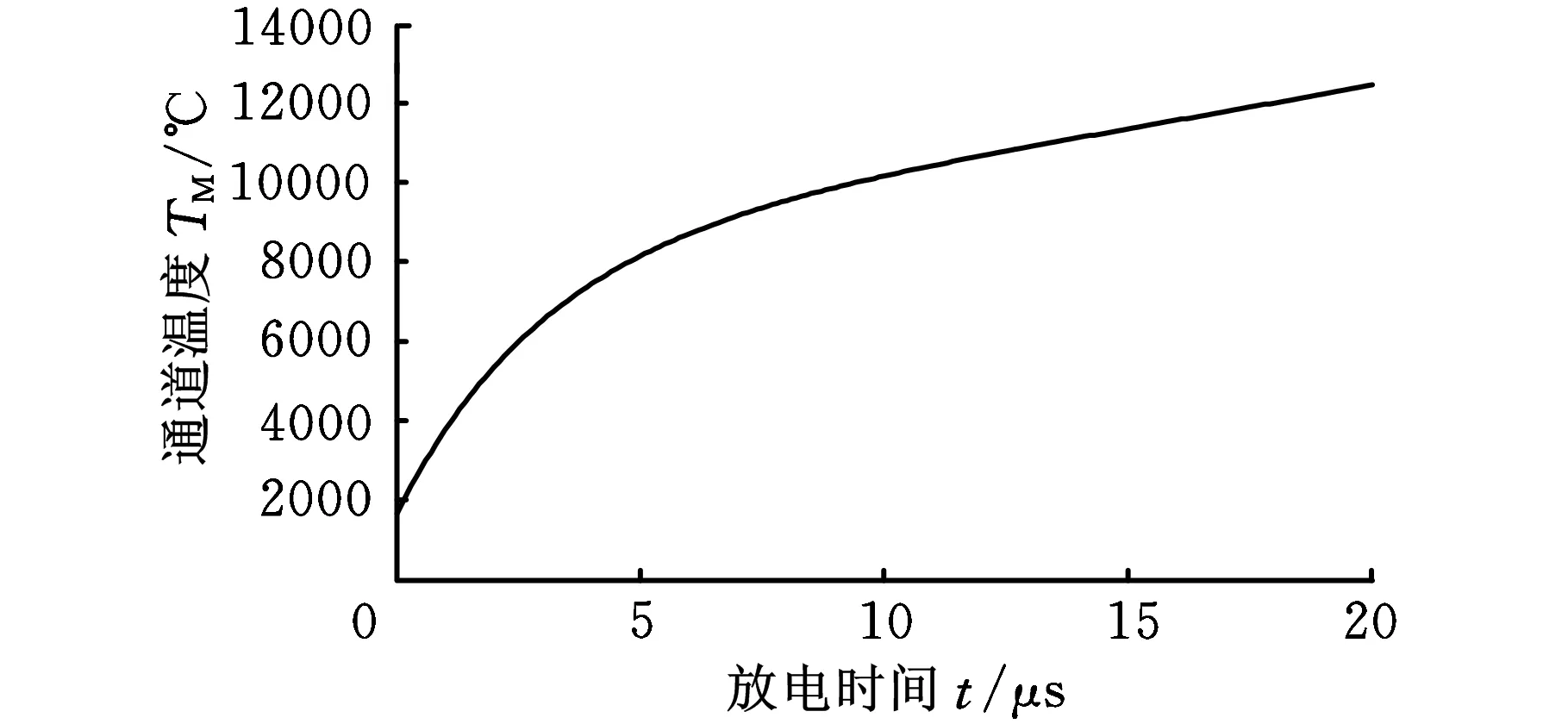
图12　Ton=20 μs放电通道温度变化图

3　试验验证

3.1试验条件

试验在苏州三光科技股份有限公司DK7625P型号的慢走丝线切割机床上进行，电极丝直径为0.2 mm，工件材料为镍基高温合金Inconel 718(φ55 mm×10 mm)。声发射传感器安装在工作台上靠近加工区域的位置，且尽量减小传感器安装位置与工件之间的连接面，以便尽可能地减少声信号的衰减。传感器接收到的声发射信号先后经过屏蔽式I/O接线盒和平衡控制器，由数据采集卡(2M/s/ch)进行采集，将采集的信号数据存储到移动硬盘中，装置连接如图13～图16所示。用Taylor Hobson粗糙度仪对加工表面粗糙度进行测量。

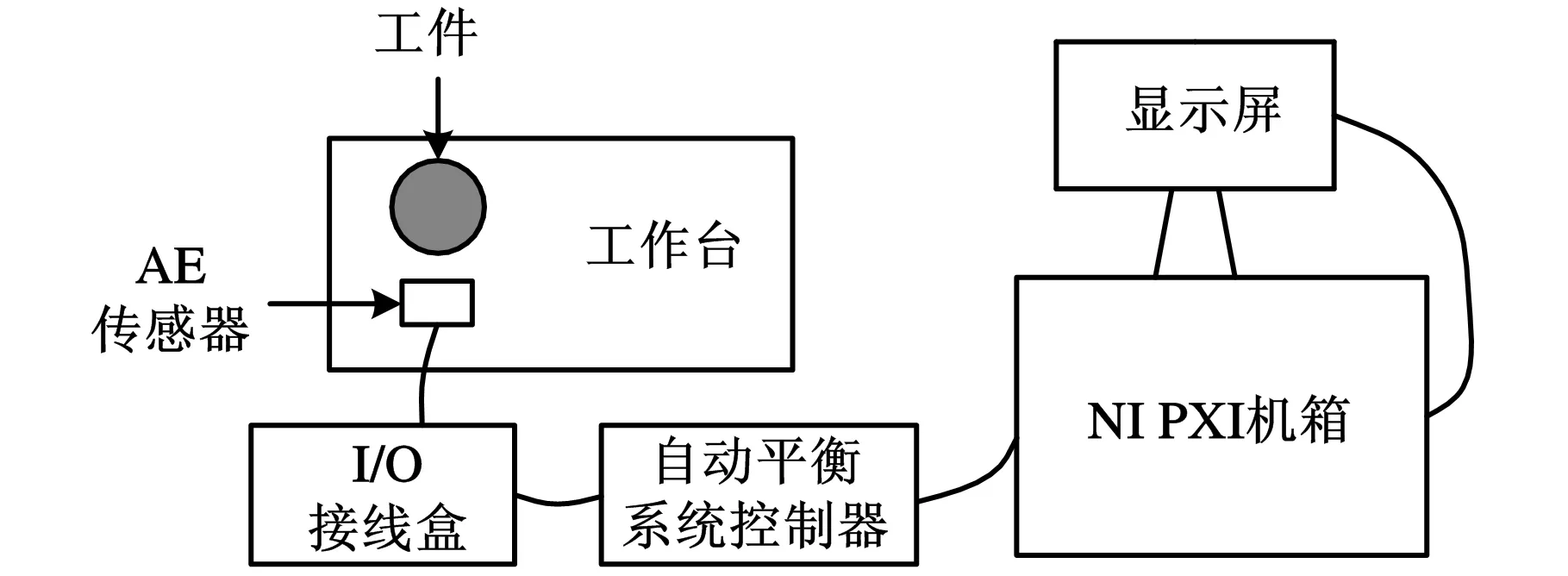
图13　试验装置连接示意图

图14　机床总体外观

图15　工件与AE传感器位置

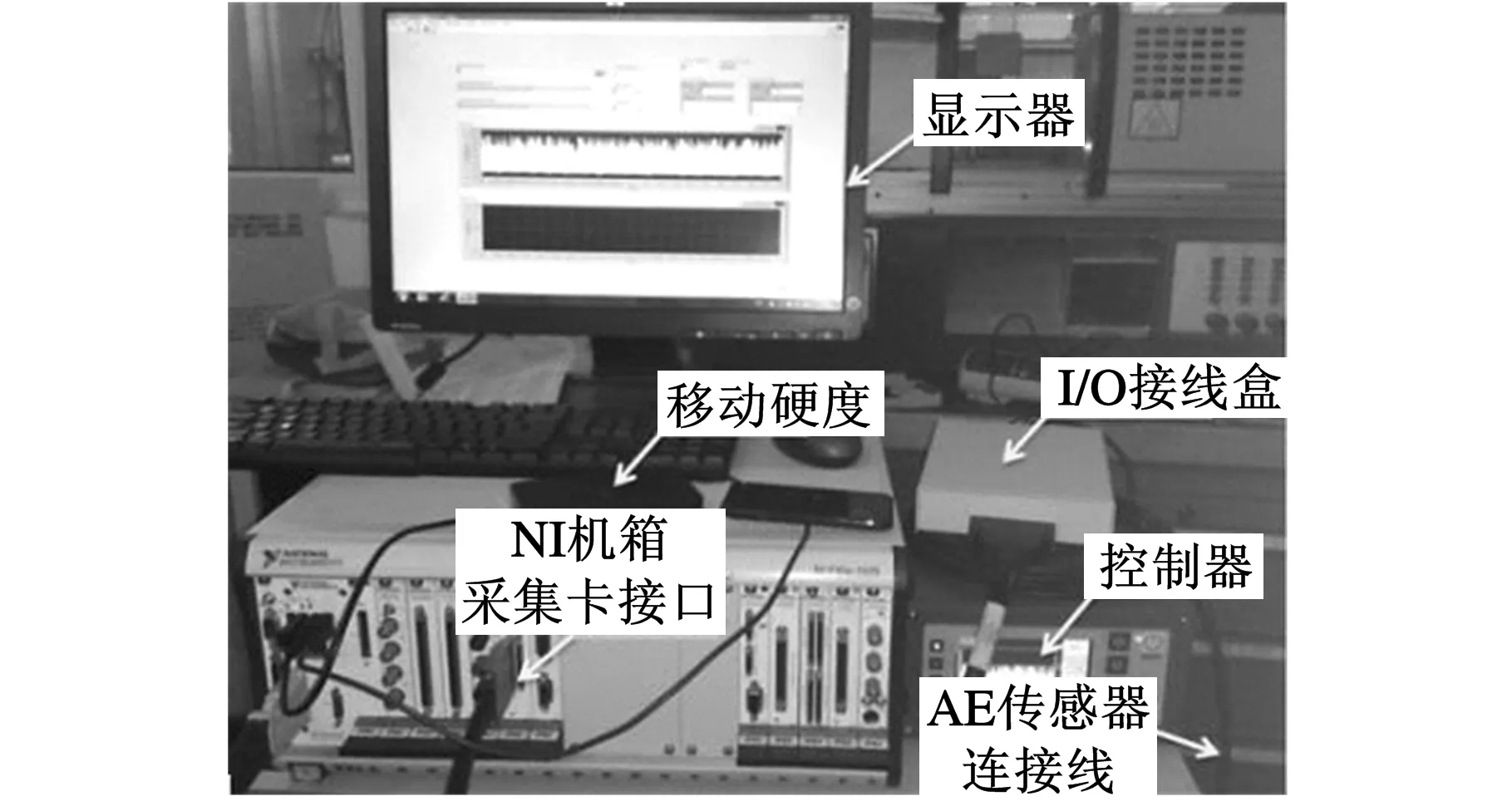
图16　AE信号采集装置实物连接图

根据慢走丝线切割加工Inconel 718的典型工况设计了五次加工工艺路线，第一次为粗加工，随后四次为精加工，分别记为M、T1、T2、N和T3，其中N为验证试验。试验通过控制脉冲时间(Ton)、脉冲间隔(Toff)和峰值电流(IP)这三个对慢走丝线切割加工表面质量影响最大的参数，设定了五组不同的参数组合，如表4所示，同时也给出了实验测得的放电电压(U)和放电电流(I)。为了粗糙度检测方便，分别用各组参数在工件上单独加工一个面。

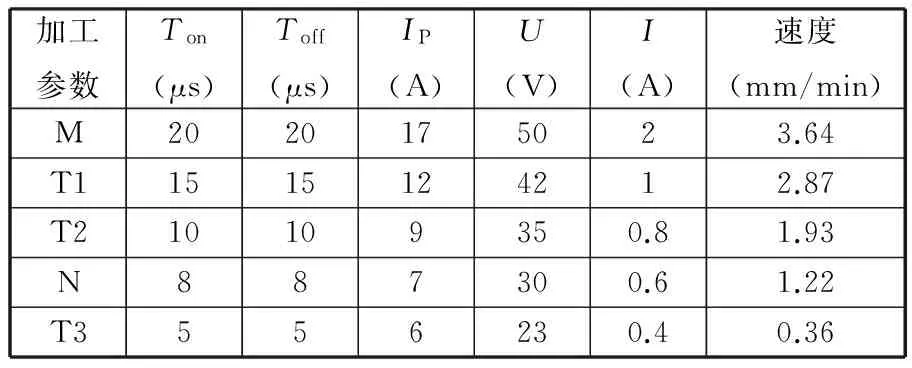
表4　加工参数

3.2粗糙度与仿真蚀坑深度对比分析

用Taylor Hobson粗糙度仪测得的各表面粗糙度如表5所示。显然从M到T3，随着放电能量逐渐减小，表面粗糙度Ra与Rt值都显著地减小了。

表5　粗糙度数据

由图17可知，对比粗糙度Rt值(轮廓表面波峰与波谷之差)与仿真蚀坑深度可以发现：仿真蚀坑深度与粗糙度的变化趋势基本一致，但始终略小于实测Rt值。两者的差值随着脉冲宽度的增大变大，这是因为慢走丝线切割加工时部分熔化的金属会重新凝固在已加工表面，增大微观表面波峰与波谷的距离，即增大了Rt值，且放电能量越高，该再铸层金属越厚，即仿真的蚀坑深度与实测Rt之间的差值越大。

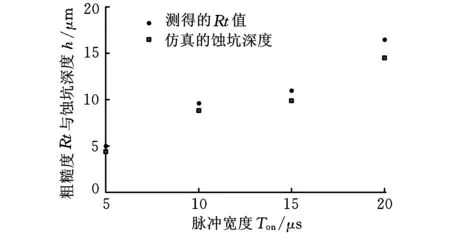
图17　仿真与试验数据对比

3.3声发射信号的处理与分析

慢走丝线切割放电加工时，声发射传感器可能会采集到很多噪声信号， 现对该过程中的噪声分析如下：机床未运行时传感器并没有采集到声发射信号，说明实验室条件下环境噪声并不会对采集信号产生干扰；慢走丝线切割工作液虽具有一定的压力，但由于是沿着电极丝流入加工区域，试验结果也证明冷却液产生的噪声也可忽略不计；此外，慢走丝线切割机床空运行时会产生较弱声信号，且其频率远小于脉冲放电的频率。陈湛清等[9]采用滤波器对机床运转噪声进行排除，但采用滤波器过滤噪声信号的同时也可能将部分有效信号过滤掉。本文通过先采集原始信号波形，再运用文献[18]中的小波分析方法对加工过程中的低频噪声进行剔除。

试验采集到的声发射信号波形如图18～图21所示。每次工艺路线设置的采集时间为300 s，因单次测量的数据太大，在LABview程序中对数据进行分段读取，每组数据被分为100段，对应的采集时间为3 s。由于Excel读取数据量的限制，这里取前1.5 s内的数据绘制声发射信号波形图，如图19～图22所示。

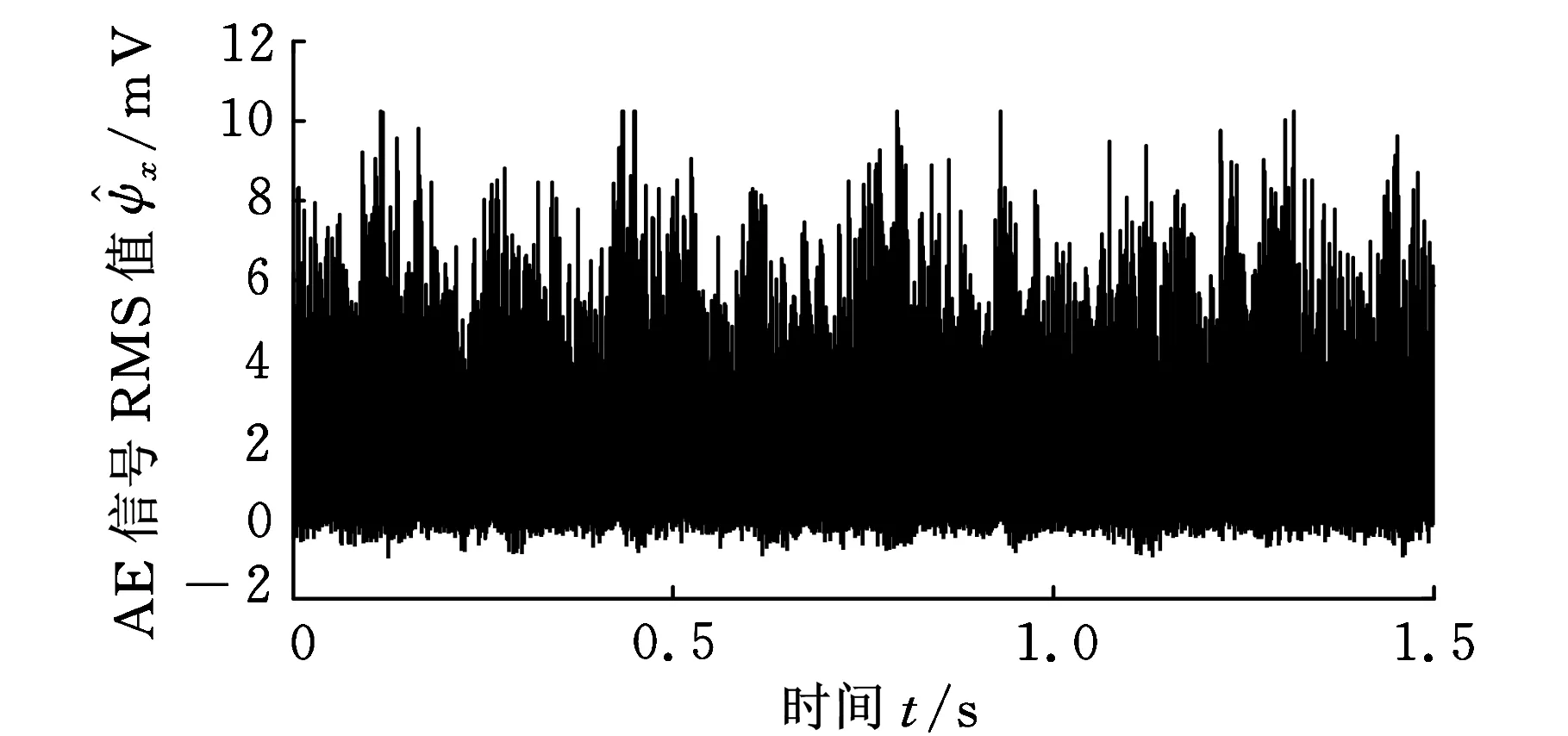
图18　M组的AE信号波形

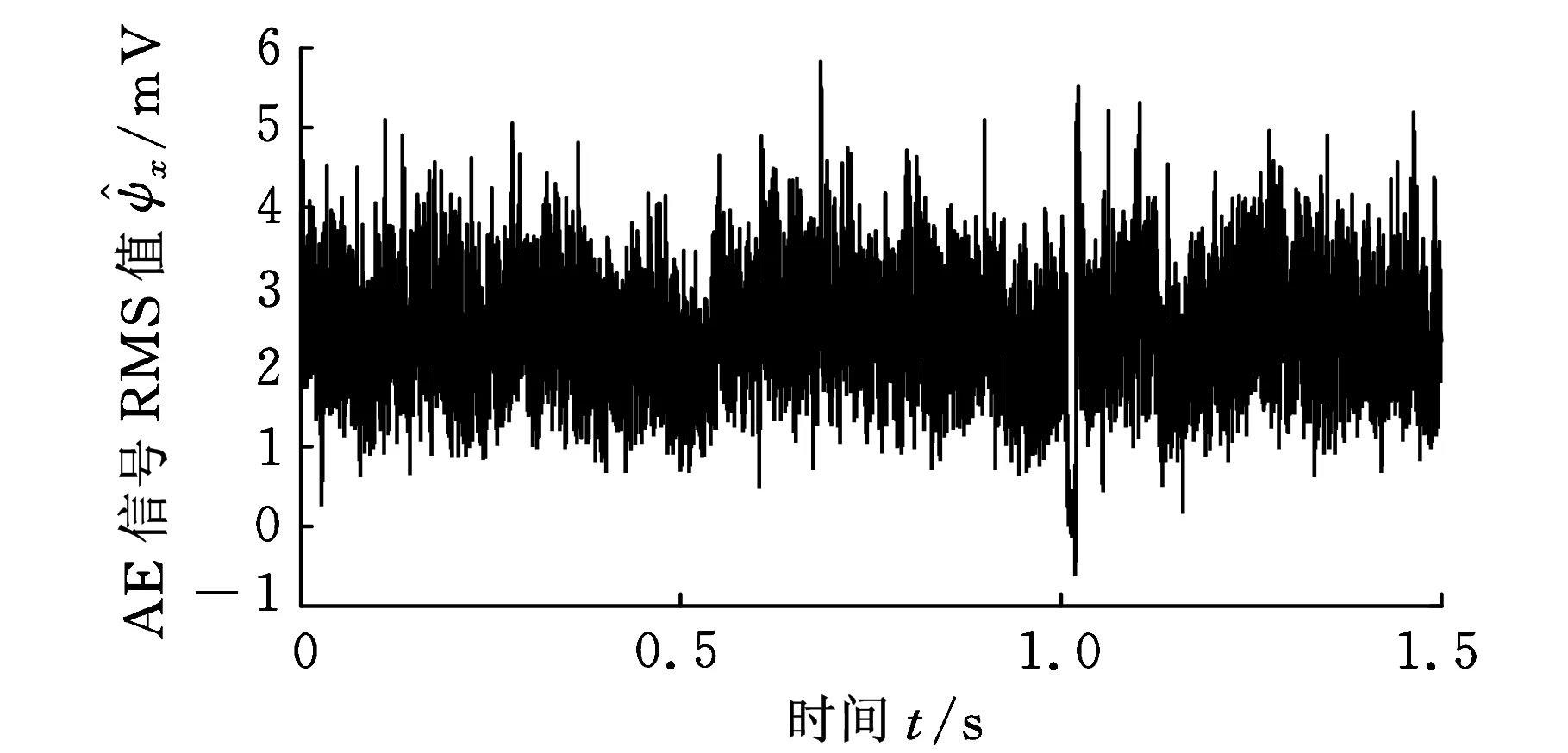
图19　T1组的AE信号波形

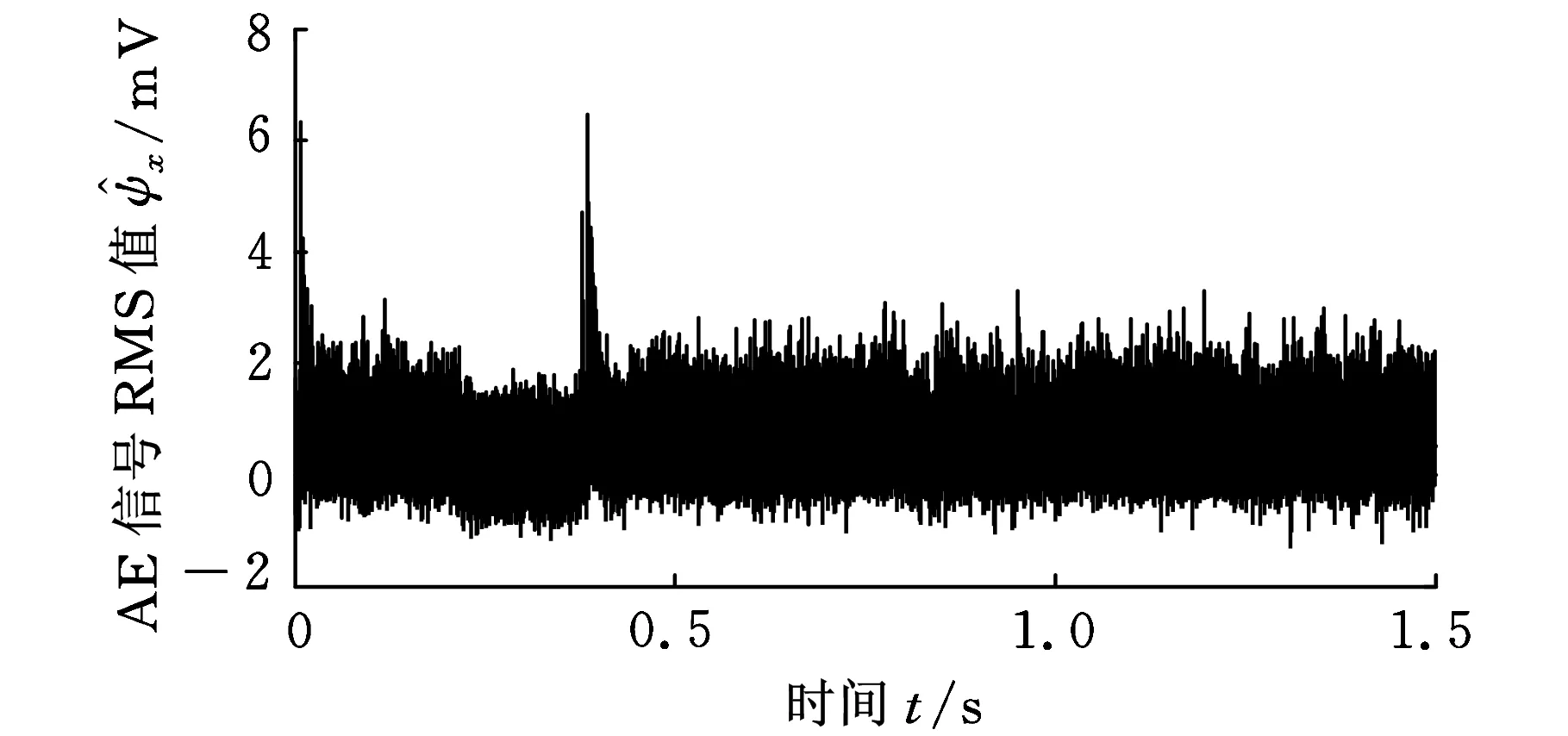
图20　T2组的AE信号波形

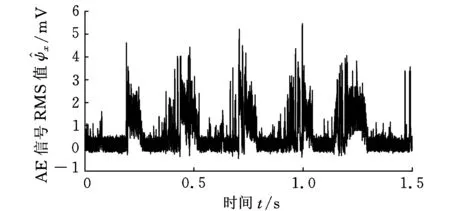
图21　T3组的AE信号波形

信号的均方根值(RMS value)描述了随机信号的强度或平均功率，可用下式定义：

(12)

式中，x(t)为随机信号的样本记录；T为样本记录时间。

本次试验采集到的声发射信号的RMS值通过LabView编写的程序计算出，图18～图21分别对应M到T3，可看出对应的RMS值也从3.86降到了0.92，说明随着放电能量的减小，声发射信号的强度也降低。

如图22所示，以M参数条件为例，为了研究单个脉冲周期内的声发射信号变化规律，将声发射信号波形图局部放大。图22中每两个尖峰之间的数据点数为20，因为每10个数据点对应的时长为15 μs，则两个尖峰之间的时长为30 μs，虽然不等于脉冲宽度20 μs，但波形图上周期性地出现尖峰，与脉冲电源的周期性仍有一定的对应关系，尖峰说明在极间介质击穿时释放出较强的声发射信号。尖锋的出现表明此时的放电能量高，而此时对应的仿真得到的放电通道的温升速度也较快。

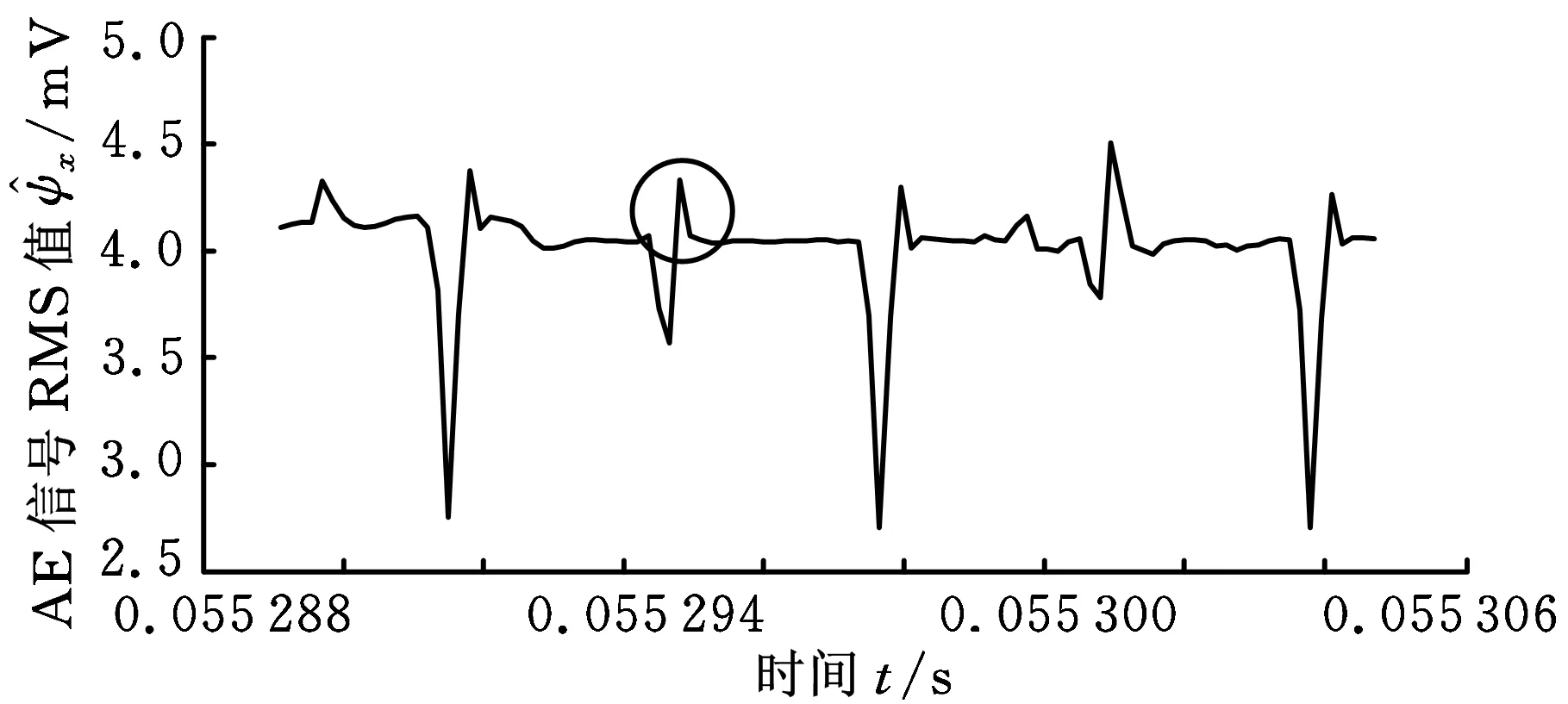
图22　M组的AE信号局部波形图

以上分析都表明，声发射信号能很好地反映放电能量的变化，而放电能量又决定性地影响加工表面质量，如粗糙度等。因此本文通过建立声发射信号RMS值与加工表面粗糙度的函数关系，对慢走丝线切割加工表面粗糙度进行预测。

3.4表面粗糙度与声发射信号RMS值的回归分析

试验测得的表面粗糙度Ra值以及声发射信号RMS值如表6所示，两者都随着放电能量的减少而减小，若能建立两者之间的对应关系，则可以根据在线测得的声发射信号RMS值直接得出工件材料表面的粗糙度值，提高加工效率。对表6中的数据作出散点图，如图23所示。用MATLAB曲线拟合工具箱拟合该四组数据，纵轴为加工工件表面粗糙度，横轴为声发射信号的RMS值。拟合得到的曲线如图24所示，曲线方程为

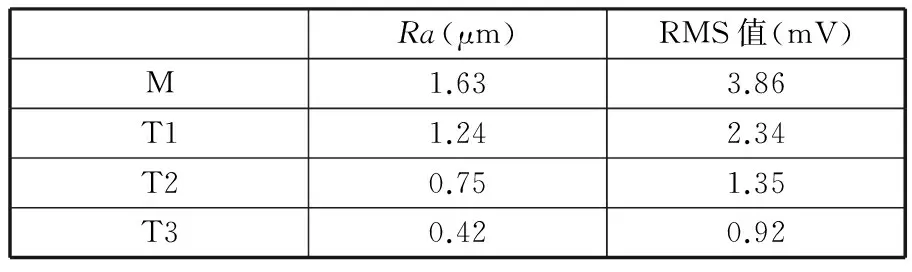
y=1.363e0.063 39x-2.085e-0.7685x　(13)

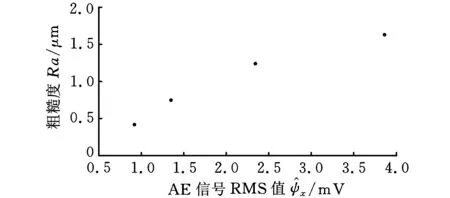
图23　粗糙度散点图

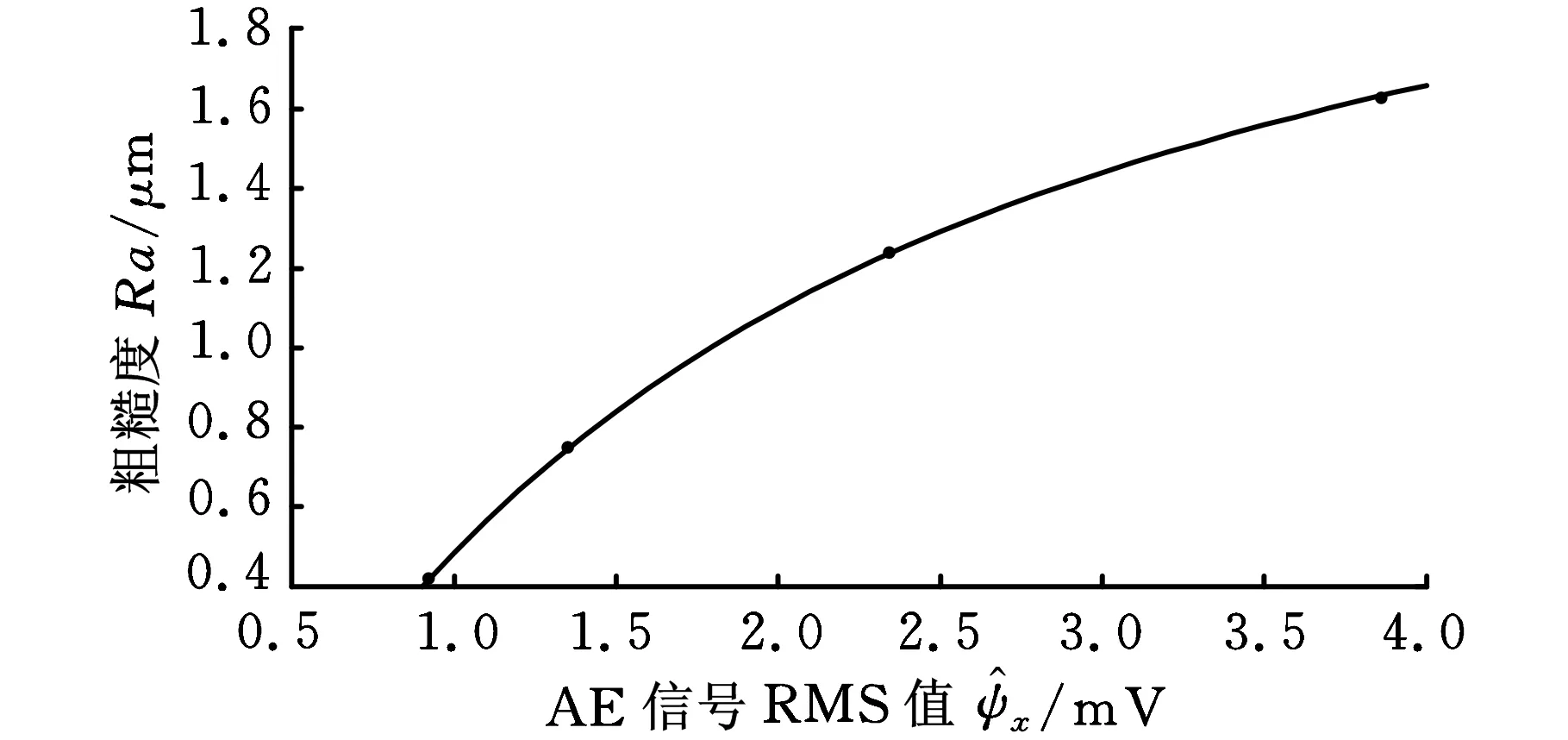
图24　多项式函数拟合曲线图

在置信区间为95%时R2≈1，和方差(SSE)为1.746×10-17。为验证方程的预测精度，进行了一组验证试验，代号为N，参数如表5所示。该参数条件下测得的粗糙度Ra为0.58 μm，实际测得RMS值为1.13 mV，根据式(13)得到的相对应的N参数条件下通道内的粗糙度Rt为0.56 μm，预测误差仅为4.40%。较小的误差说明该模型可以用来监测Inconel 718工件材料的表面粗糙度。

因此对于某种特定材料，都可以通过试切割首先建立数学函数模型，在之后的加工过程中都可以直接根据该函数关系求出工件表面的粗糙度，从而缩短停机检测的时间，大大地提高慢走丝线切割的加工效率。

4　结论

(1)进行了基于圆台形热传导模型的有限元分析。放电通道内的最高温度与脉冲能量正相关，放电能量足够大时放电通道内的最高温度可达10 000 ℃以上。对于Inconel 718材料， 在脉冲电源占空比为1∶2时，20 μs脉冲宽度可作为区分加工过程是气化还是熔化去除为主的一个临界值。

(2)理论放电蚀坑深度与表面粗糙度Rt值的变化趋势相一致，因此可通过仿真计算估计加工工件的表面粗糙度。

(3)声发射波形图上的尖峰信号与同一时间内放电通道内温升变化的一致性表明，通过分析声发射信号，能够为研究放电通道内的能量变化规律提供理论依据。

(4)回归分析得到的工件表面粗糙度值与声发射信号RMS值数学模型预测误差低于4.40%，说明可以采用声发射检测技术对慢走丝线切割加工工件表面粗糙度进行在线监测。

[1]李丽，魏修亭，程祥,等. Inconel 718镍基高温合金电火花加工表面完整性初步研究[J]. 功能材料,2012,43(24):3479-3483.

Li Li, Wei Xiuting, Cheng Xiang, et al. Study of Surface Integrity of Inconel 718 in EDM [J]. Functional Materials, 2012,43(24):3479-3483.

[2]Guo Y B, Li W.Surface Integrity Characterizationand Prediction in Machining of Hardened and Difficult-to-machine Alloys: a State-of-art Research Review and Analysis[J]. Machining Sci. Tech.,2009,13(4):437-470.

[3]Eubank P T, Patel M R, Barrufet M A, et al. Theoretical Models of the Electrical Discharge Machining Process-Ⅲ: the Variable Mass, Cylindrical Plasma Model[J]. Journal of Applied Physics, 1993, 73(11): 7900-7909.

[4]Xia Heng, Kunieda M, Nishiwaki N. Removal Amount Difference between Anode and Cathode in EDM Process[J]. International Journal of Electrical Machining, 1996, 1:45-52.

[5]李建，刘志东，邱明波,等.单晶硅放电蚀除机理研究及有限元分析[J]. 中国机械工程,2010,21(7):847-851.

Li Jian, Liu Zhidong, Qiu Mingbo, et al. Study and FEM Analysis on Discharge Erosion Mechanism of Monocrystalline Silicon[J]. China Mechanical Engineering,2010,21(7):847-851.

[6]Izquierdo B, Sanchez J A, Plaza S, et al. A Numerical Model of the EDM Process Considering the Effect of Multiple Discharges[J]. International Journal of Machine Tools & Manufacture,2009,49:220-229.

[7]Claudio A. Utilizing Acoustic Emission Testing to Detect High-temperature Hydrogen Attack (HTHA) in Cr-Mo Reformer Reactors and Piping during Thermal Gradients[J]. Procedia Engineering,2011,10:3552-3560.

[8]El-Menshawy M F,Bhattacharyya S K. The Use of Acoustic Techniques for Monitoring and Controlling the EDM Process[C]//Proceedings of 19th International MTDR Conference.International Journal of Machine Tool Design and Research.London: Elsevier,1978: 559-563.

[9]陈湛清,奚绍申,胡德金,等. 电火花加工中声频谱的初步探索[J]. 电加工,1982(4):1-4.

Chen Zhanqing, Xi Shaoshen, Hu Dejin, et al. Investigate on Acoustic Spectrum in EDM[J]. Electrical Machining, 1982(4):1-4.

[10]Craig S,Philip K. Applications of Acoustic Mapping in Electrical Discharge Machining[J]. CIRP Annals-Manufacturing Technology,2013,62(1):171-174.

[11]Muslim M,Gunawan S P,Takashi E,et al.Material Removal and Fracture Detection in Micro-EDM Processes[J]. Key Engineering Materials,2011,462/463:1092-1096.

[12]Janardhan V,Samuel G L. Pulse Train Data Analysisto Investigate the Effect of Machining Parameters on the Performance of Wire Electro Discharge Turning (WEDT) Process[J]. International Journal of Machine Tools and Manufacture,2010,50(9):775-788.[13]李明辉. 电火花加工理论基础[M]. 北京：国防工业出版社,1989.

[14]Perez B, Witz G, Flükiger R. Properties of the Plasma Channel in Liguid Discharges Inferred from Cathode Local Temperature Measurements[J]. Journal of Applied Physics,2005,98(11): 113305-113310.

[15]Descoeudres A, Hollenstein C, Wälder, et al. Time-resolved Imaging and Spatially-resolved Spectroscopy of Electrical Discharge Machining Plasma[J]. Journal of Applied Physics, 2005,38:4066-4073.

[16]Han Fuzhu, Cheng Gang, Feng Zhijing, et al. Thermo-mechanical Analysis and Optimal Tension Control of Micro Wire Electrode[J]. International Journal of Machine Tools & Manufacture, 2008,48:922-931.

[17]Cheng Gang, Han Fuzhu, Feng Zhijing. Experimental Determination of Convective Heat Transfer Coefficient in WEDM[J]. International Journal of Machine Tools & Manufacture, 2007,47:1744-1751.

[18]康玉梅,朱万成,白泉,等. 基于小波变换时频能量分析技术的岩石声发射信号时延估计[J]. 岩石力学与工程学报,2010,29(5):1010-1016.

Kang Yumei, Zhu Wancheng, Bai Quan, et al. Time-delay Estimation of Acoustic Emission Signals of Rock Using Time-frequency Energy Analysis Based on Wavelet Transform[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(5):1010-1016.

(编辑王艳丽)

Simulation and Experiments of WEDM-LS Based on Truncated Cone-shaped Thermal Conduction Model

Wang Yan1Yang Lin1Ding Chengcai2Ding Chengye3

1.University of Shanghai for Science and Technology,Shanghai,200093 2.Taizhou Jiangzhou NC Machine Tools Manufacturing Co.,Ltd.,Taizhou,Jiangsu,225300 3.Nanjing Communications Institute of Technology,Nanjing,210000

On the basis of formation mechanism of plasma channel in WEDM, a novel heat conduction model with a circular truncated cone shape was put forward for the first time by studying the velocity difference of electrons and ions in plasma channel. Based on this heat conduction model a finite element analysis was conducted considering the typical machining conditions of aeronautical material-Inconel 718 in WEDM to research its the machining mechanism. The influences of discharge energy on maximum temperature of plasma channel and depth of discharge crater were studied systematically. A verification experiment was carried out,which firstly employed acoustic emission testing technology to monitor the machined surface roughness. It shows that the simulation results are in good agreement with measured Rt values of surface roughness. The analysis results of acoustic emission signals collected during the machining process of WEDM reveal that the intensity of acoustic emission signals get stronger with the increase of discharge energy and get weaker as the changing rate of maximum temperature of discharge channel becomes slower. A regression analysis of value of surface roughness and root-mean-square (RMS) value yields a mathematical prediction model with high precision, the error is less than 4.40%.

Inconel 718; wire electrical discharge machining(WEDM); truncated cone-shaped thermal conduction model; finite element; acoustic emission; regression analysis

2014-11-11

上海市研究生创新基金资助项目(JCWCXL1302)；江苏省创新创业项目

TG661< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.05.006

王艳，女，1969年生。上海理工大学机械工程学院教授、博士。研究方向为精密加工与特种加工。发表论文60余篇。杨林(通信作者)，男，1989年生。上海理工大学机械工程学院硕士研究生。丁成才，男，1974年生。泰州市江洲数控机床制造有限公司工程技术研究中心工程师。丁成业，男，1977年生。南京交通职业技术学院机电工程学院副教授。