起重机变幅运动吊重防摆控制研究

曹旭阳　袁　靖　李万里　丁　冲

1.大连理工大学，大连，116024　　2.中国一拖集团有限公司，洛阳，4710393.大连益利亚工程机械有限公司，大连，1160244.大连船舶重工集团有限公司，大连，116024

起重机变幅运动吊重防摆控制研究

曹旭阳1袁靖2李万里3丁冲4

1.大连理工大学，大连，1160242.中国一拖集团有限公司，洛阳，4710393.大连益利亚工程机械有限公司，大连，1160244.大连船舶重工集团有限公司，大连，116024

针对起重机变幅运动过程中吊重摆动造成的就位精度差、工作效率低和作业不安全等问题，提出了一种误差渐进补偿控制方法，以减小吊重摆动。在分析误差渐进补偿控制原理的基础上，设计了误差渐进补偿控制器。采用变补偿系数控制方法，在实现吊绳摆角渐进减小的同时满足了变幅加速度和液压泵排量的要求。运用MATLAB软件对系统进行仿真，仿真结果表明，对于不同的绳长和臂架长度，误差渐进补偿控制具有良好的鲁棒性和控制精度，在起重机开始制动后，吊绳摆角在10 s内减小到了0.003 rad以下。

起重机；变幅运动；吊重摆动；误差渐进补偿控制器

0　引言

关于起重机的吊重防摆控制方法，国内外学者做了大量研究，主要包括：输入整形控制法[1-2]、最优控制法[3-4]、自适应控制法[5]、模糊控制法[6]、滑模控制法[7]、时滞控制理论[8]等。上述控制方法均有优缺点，总体还存在一些问题：首先，在设计控制器时着重考虑吊摆机构，对动力机构及两者中间的速度转换机构考虑较少，特别是在变幅工况下，臂架变幅速度与变幅油缸伸缩速度或变幅卷筒的收放绳速度之间存在的非线性会提高控制难度；其次，在设计控制算法时，着重考虑控制效果，对输入信号的可获取性及控制算法实用性考虑较少；此外，很多控制算法是建立在对模型线性化处理的基础上的，对于系统存在的非线性和时变性，控制效果不理想。

本文建立了较完整的变幅系统模型，在分析误差渐进补偿控制原理的基础上，设计了误差渐进补偿控制器，在给定的控制法则下，对吊绳摆角信号运算处理后进行反馈，实现了变增益反馈控制。综合考虑变幅加速度和液压泵排量，合理设计两阶段的补偿系数，实现了吊重摆角的渐进减小。在满足多工况、存在初始状态等控制要求的同时，设计了位置控制器，减小了变幅角度误差。

1　变幅系统

变幅系统是起重机工作系统的重要组成部分。起重机变幅作业时，变幅系统通过改变臂架俯仰角，使吊重靠近或远离回转中心。臂架俯仰角的增大和减小分别对应着起重机的向上和向下变幅。图1为动臂式起重机向上变幅时吊重的运动轨迹图，臂架俯仰角增大β时，吊重由位置A运动到位置B，吊重靠近回转中心，完成向上变幅动作。相反，当臂架俯仰角减小时，吊重远离回转中心，完成向下变幅动作。

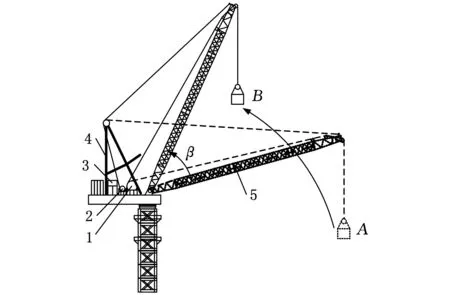
1.起升卷筒　2.变幅卷筒　3.动力单元　4.人字架　5.臂架图1　吊重运动轨迹

起重机变幅系统主要由液压系统、中间速度转换机构和吊摆机构组成。其中，液压系统为变幅机构的驱动系统，液压泵通过液压系统控制液压马达转动；中间速度转换机构为变幅马达转速或液压缸伸缩速度与臂架变幅角速度之间的速度传递机构；吊摆机构为变幅作业时的吊重摆动机构。起重机变幅作业时，输入电流信号通过控制液压泵斜盘摆角来改变液压泵排量，从而改变马达转速，马达经变幅减速机带动变幅卷筒转动，控制变幅绳的收放，变幅绳拉动臂架，从而使臂架俯仰角发生变化。

2　系统建模

2.1吊摆机构建模

图2所示为吊摆机构的简化模型。θ为吊绳在变幅平面内的摆角，Lb为臂架长度，l为绳长，β为变幅角度。对图中简化模型作如下假设[9]：①臂架视为刚体，不考虑吊绳的质量和弹性伸缩；②将吊重简化为一质点，忽略空气阻尼及摩擦阻尼的影响；③臂架长度、臂架变幅角度、吊绳长度及吊绳在变幅平面内的摆角均是可测量的。

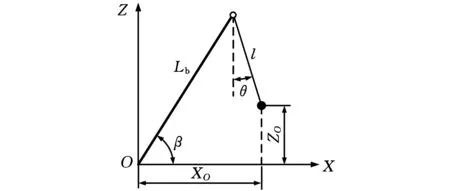
图2　吊摆机构简化模型

由图2可知，吊重位置坐标可以由下式给出：

(1)

式中，XO、ZO分别为吊重水平和竖直坐标。

在忽略吊绳质量后，吊绳与吊重组成的摆动系统的动能T及势能V分别为

(2)

式中，m为吊重质量；g为重力加速度。

将式(1)、式(2)代入下述拉格朗日方程：

(3)

由于θ较小，近似认为：sinθ≈θ，cos(β-θ)≈cosβ，sin(β-θ)≈sinβ，可得

(4)

2.2中间速度转换机构建模

以动臂塔式起重机为例，中间速度转换机构主要包括变幅减速机、变幅卷筒、人字架、变幅绳、臂架等，其简化模型如图3所示(省略变幅减速机及变幅卷筒)。图中，O为回转中心，C、F分别为人字架前后安装绞点，D点为定滑轮的位置，E点为动臂塔机臂架根绞点。CE、CD和DE之间的距离分别为lc、ld和la，DE与CE的夹角为α。

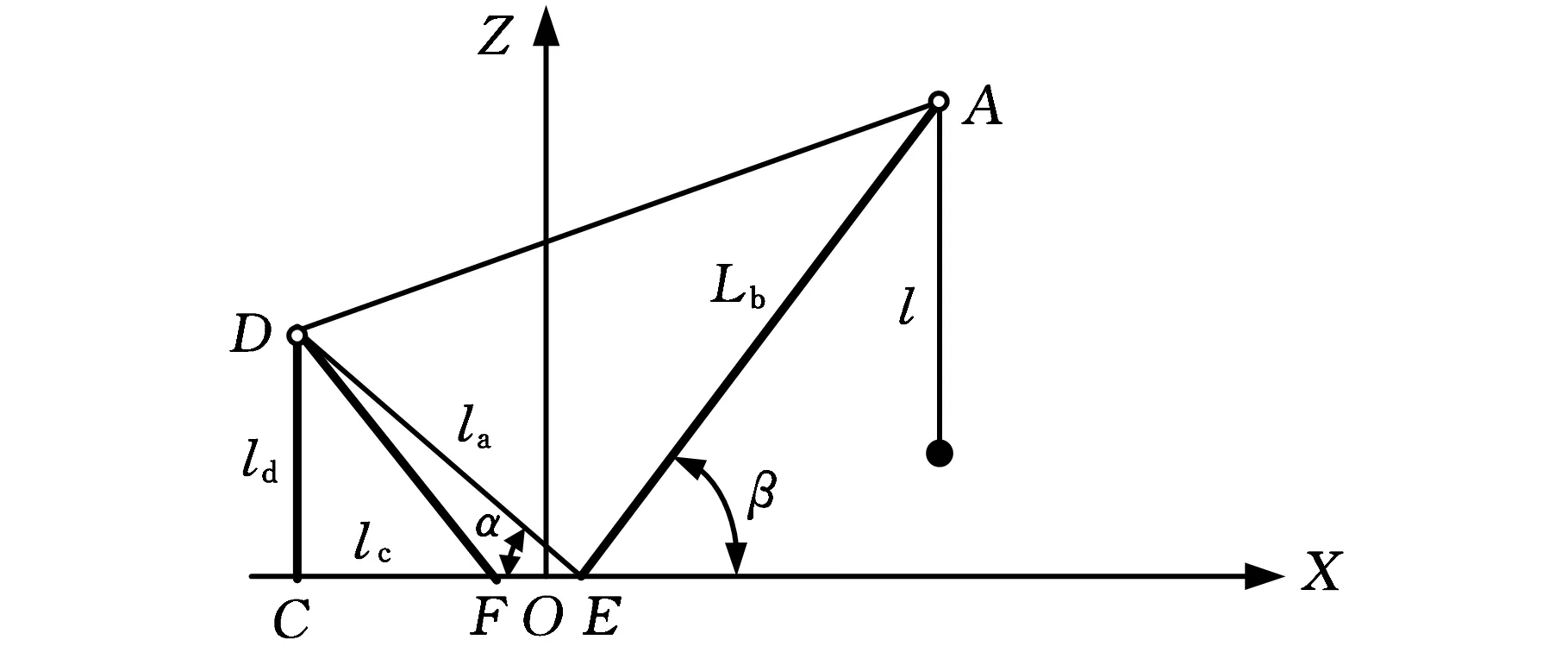
图3　中间速度转换机构简化模型

当臂架在图3所示位置时，由几何关系可得

(5)

设变幅绳绳速为v，规定变幅绳收绳时绳速为正，由式(5)可得

(6)

设ωm为液压马达转速，i为总减速比，d为变幅卷筒直径，n为变幅倍率，则

(7)

2.3液压系统建模

变幅机构的液压系统可采用闭式系统或开式系统，本文以闭式系统为例。系统传递函数主要由两部分组成：控制斜盘摆角的阀控缸环节和泵控马达环节。

通常，变量机构的谐振频率比泵控马达系统的液压固有频率大得多，而伺服阀的频宽又比变量机构的谐振频率大得多，因此伺服阀控制变量缸的位置闭环传递函数可简化为[10]

(8)

式中,Xφ为变量缸活塞杆位移；I为输入电流；Kf x为位置反馈系数；ωx为变量缸位置环的转折频率。

液压马达转速对变量缸活塞杆位移的传递函数为

(9)

式中，Kφ为斜盘摆角系数；ζh为液压阻尼比；ωh为液压固有频率；Dm为马达最大排量；Kqp为变量泵流量增益。

3　控制器的设计

3.1误差渐进补偿控制原理

误差渐进补偿控制的基本思想是通过改变臂架的俯仰角度来补偿吊绳的摆角。通过合理设计反馈信号，加入到操作者的输入信号中，构成期望的参考信号，使起重机在期望的输入信号控制下变幅作业。t0时刻，将吊摆机构在变幅平面内进行投影，如图4所示。其中，β0为操作者的输入，为了消除吊绳摆角θ，需要补偿的变幅角度为Δβ，此时系统的期望参考变幅角度为βr。

图4　吊摆机构在XZ平面内投影图

对于依靠臂架变幅的起重机而言，变幅作业时，误差渐进补偿控制实际上是以变幅平面内的吊绳摆角作为反馈信号，采用变增益反馈控制，通过设计适当的反馈增益，保证吊绳摆角在逐渐减小的同时，臂架的变幅加速度也能保持在一定的范围内。

3.2反馈信号的设计计算

通常情况下，起重机变幅作业时的绳长l较大，吊摆机构的谐振频率远小于液压系统模型中阀控缸位置环的转折频率ωx和液压固有频率ωh，可将其简化为一个比例环节，在控制器设计时暂不考虑液压系统及中间速度转换机构，以变幅绳速度v作为输入。由式(5)可知：

(10)

此时所需的变幅绳补偿绳长设为ΔlAD。对式(10)进行化简，并进行线性化处理可得

(11)

取以下控制法则：

ΔlAD=kΔv

(12)

式中，Δv为t0时刻所需的变幅绳补偿速度；k为时间放大系数。

由图3中的几何关系并结合式(12)，同时由于Δβ较小，近似认为cosΔβ≈1、sinΔβ≈Δβ，可得

(13)

取补偿系数λ=1/k，考虑到实际变幅速度较慢，同时要求运动平稳，为实现逐渐消除吊绳摆角，要求补偿系数λ∈(0，1)。规定变幅绳收绳时绳速为正。t0时刻，结合式(13)有

(14)

考虑液压系统及中间速度转换机构，设二者的总增益为ks，则

(15)

结合式(15)，同时替换β0为任意变幅角度β，则反馈信号ΔI为

(16)

3.3控制法则设计

操作者输入信号如图5所示。其中，ts、Δts、tm、Δtn、tn分别为开始制动时间、制动时间、制动结束时间、防摆调节时间、停止工作时间。

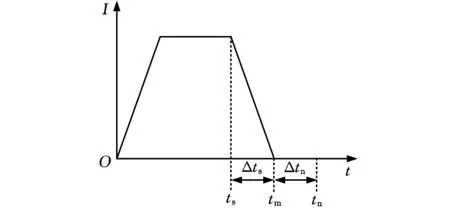
图5　操作者输入信号

误差渐进补偿控制器控制法则设计如下：

(17)

由式(17)可知，当其他参数相同，λ一定时，吊绳摆角越大，反馈信号ΔI越大，当吊绳存在较大的初始摆角时，在初始启动时刻，ΔI较大。实际上，由于输入电流信号对应着变量泵的排量，过大的输入信号，变量泵的排量不能提供。同时，输入电流信号变化过大，会使臂架变幅速度在初始启动阶段发生突变，产生较大的加速度。而过大的变幅加速度在实际应用中是不允许的。以动臂塔式起重机为例，由文献[11]可知，其变幅时起重臂头部水平移动的最大加减速度不大于0.6m/s2。

综合考虑臂架头部水平移动的最大加减速度和液压泵排量，同时保证起重机在变幅作业结束后，吊重摆角能够快速衰减，可采用变补偿系数控制，即：从开始启动到制动结束阶段，λ取较小值；制动结束到停止工作，λ取较大值。采用如下控制法则：

(18)

其中，λ1、λ2分别为两阶段的补偿系数，且λ1<λ2。λ1、λ2的值可根据起重机实际变幅工况选取。

为了在保证消摆的同时，减小变幅角度的误差，本文设计了位置控制器，由于起重机在变幅工作时，期望变幅角度是未知的，实际应用中控制器设置时可以将操作者开始制动时的变幅角度近似为期望角度。

设ΔI1为位置控制反馈信号，控制法则设计如下：

(19)

式中，KP为比例增益；βs为期望变幅角度。

在无反馈控制时操作者的输入信号设为I，控制后实际输入电流信号Ir为

Ir=I+ΔI-ΔI1

(20)

控制原理框图见图6。

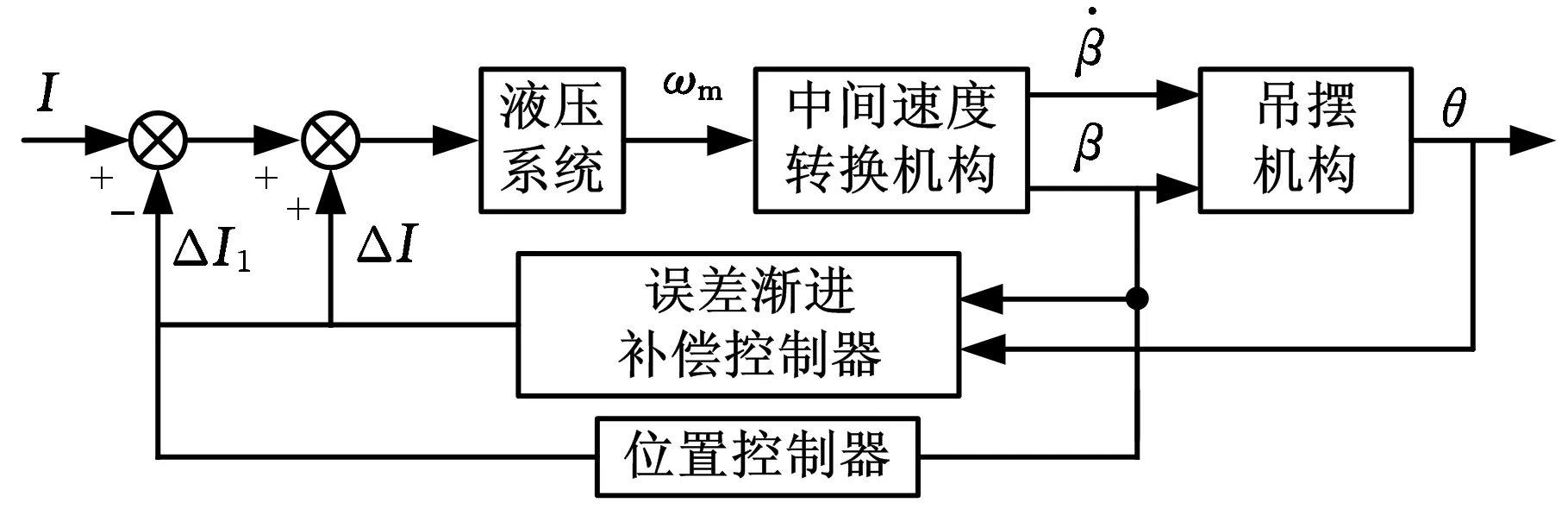
图6　控制原理框图

4　仿真实验与分析

4.1仿真模型

以16 MN·m动臂塔机为例，各参数依据样本和实际工况选取，建立Simulink仿真模型，如图7所示。

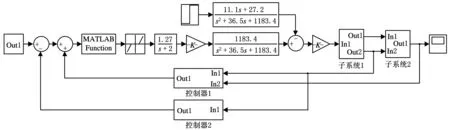
图7　系统仿真模型

建模时考虑了液压泵控制中位死区，同时设计了死区信号转换器。图7中，控制器1、控制器2分别为误差渐进补偿器和位置控制器，子系统1、子系统2分别为中间速度转换机构与吊摆机构模型。

4.2仿真结果与分析

一般情况下，起重机不工作时，吊绳的初始摆角主要由风载荷引起。由参考文献[11]可知，当迎风面积无法确定时，作用在起吊物品上的风载荷按额定起重量重力的3%计算，由此可计算出，在风力作用下，吊绳的初始摆角最大为0.03 rad。结合实际变幅工况下吊绳长度、臂架长度、臂架俯仰角的各自变化范围，设定初始绳长为30 m，臂架长度为50 m，臂架初始俯仰角为0.35 rad，吊绳初始摆角为0.03 rad。

为了能够更好地观察防摆控制效果，工作停止时间取足够大。本文选取的λ1、λ2值分别为0.05、0.35，以0.352 A为操作者的起始输入电流信号，以0.82 A为稳定输入电流信号， 启动与制动时间均为2 s，吊重初始速度为0.01 rad/s，考虑起升工况，起升绳速为0.3 m/s，持续时间为15 s。将第70 s设为开始制动时间，仿真时间为120 s。图8～图12分别为吊绳摆角响应、臂架臂头水平加速度、实际输入信号、变幅角度和吊绳绳长变化曲线。其他参数不变，将臂架长度由50 m改为70 m，吊绳摆角响应如图13所示。

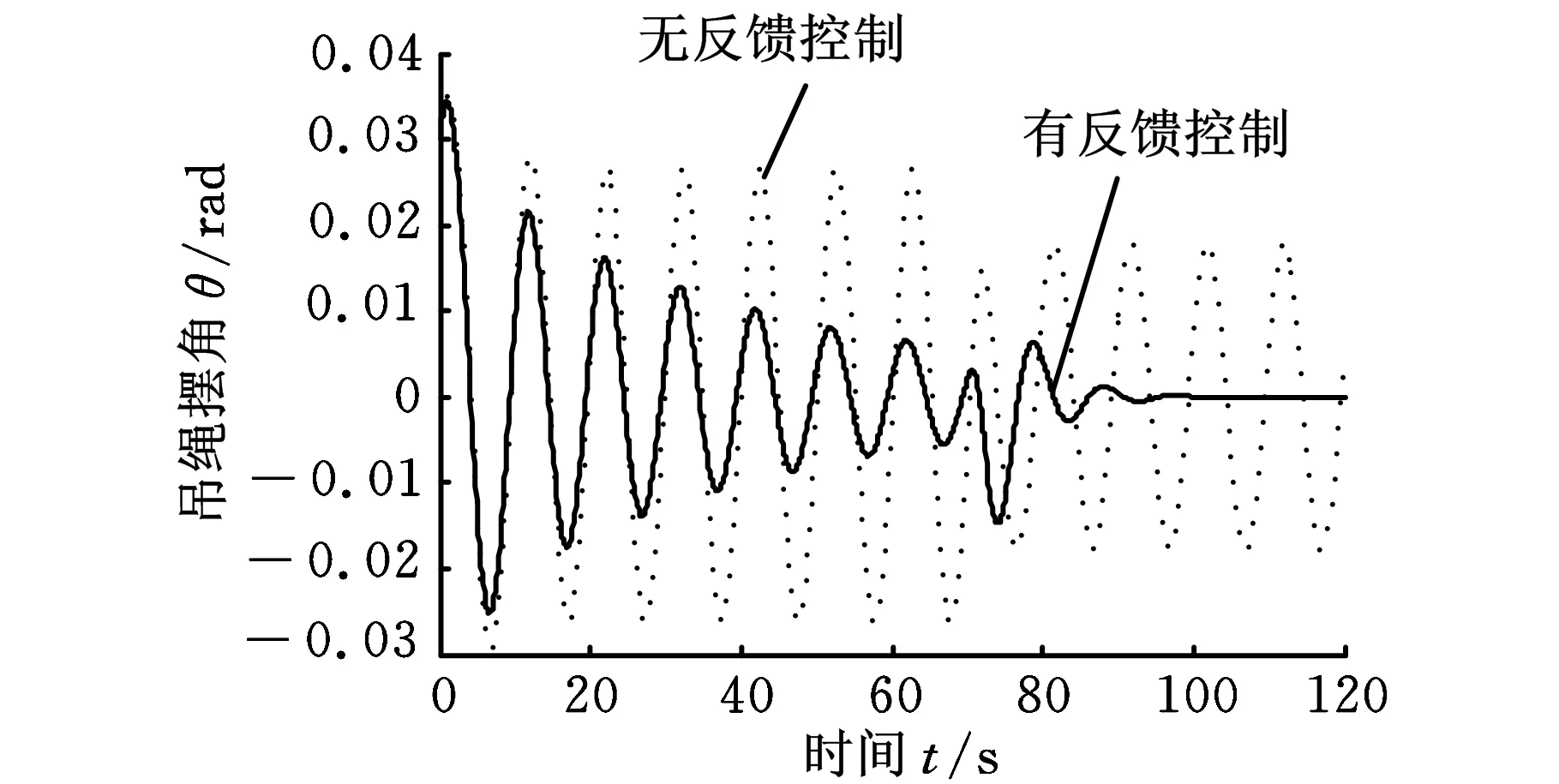
图8　吊绳摆角响应

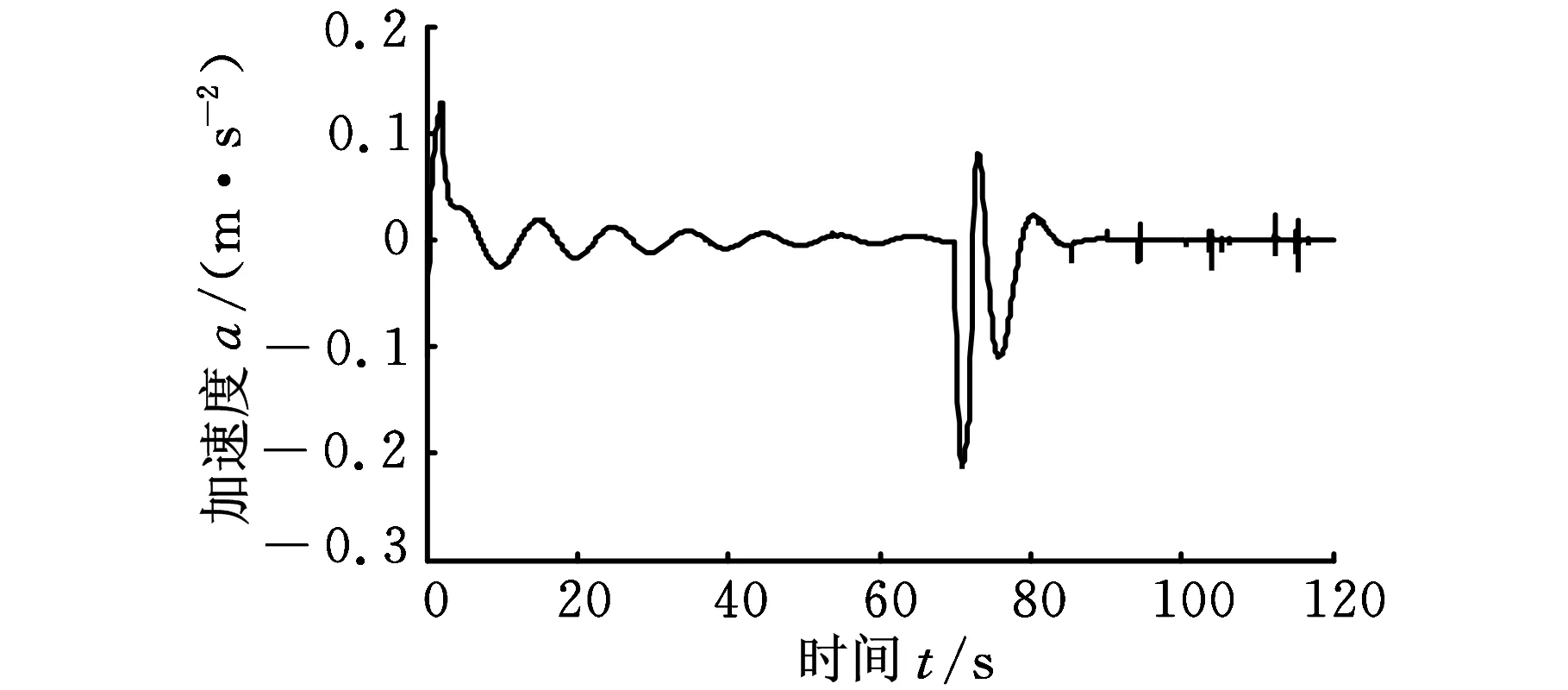
图9　臂头水平加速度

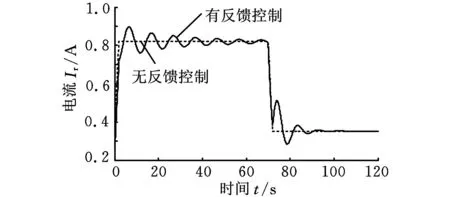
图10　实际输入信号

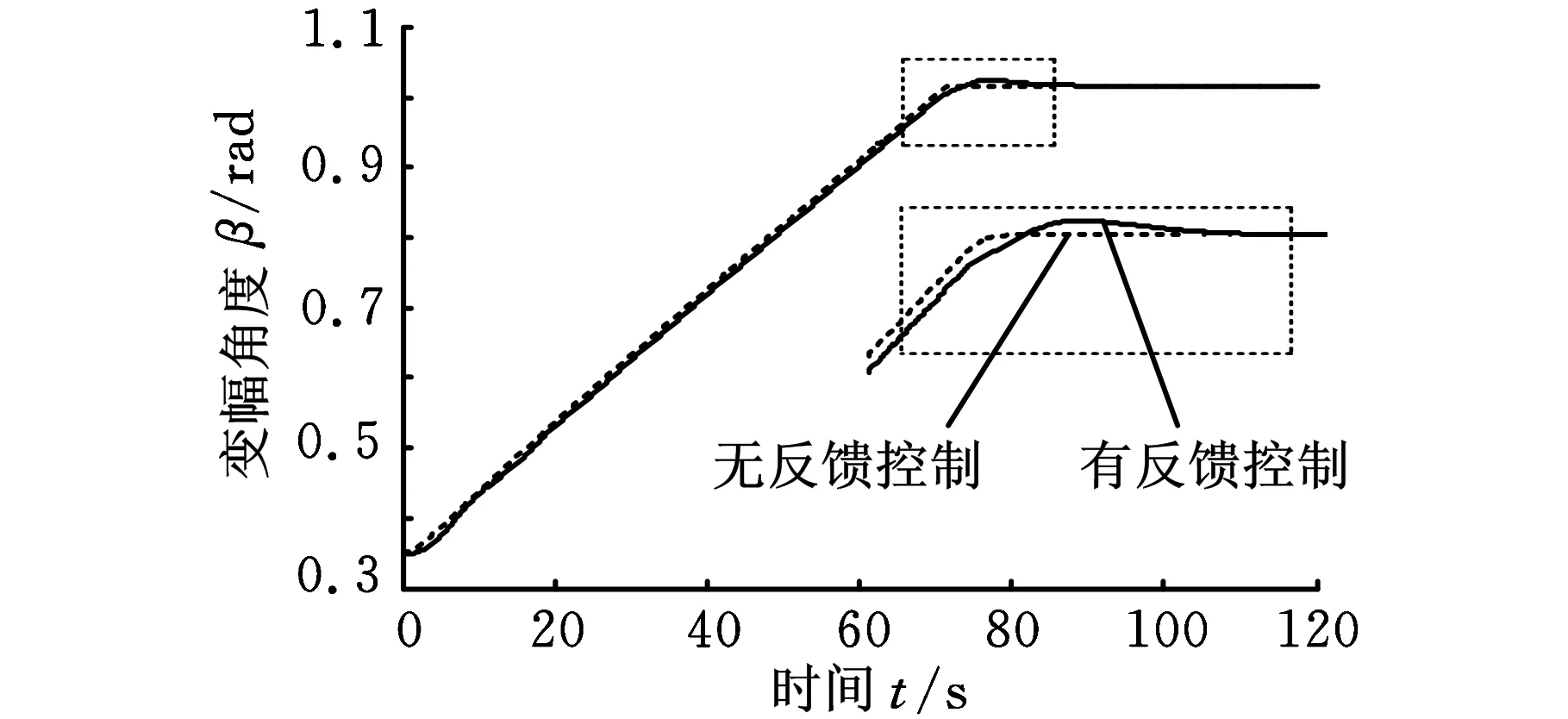
图11　变幅角度

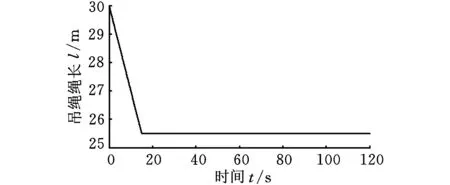
图12　吊绳绳长变化

图13　70 m臂长时的吊绳摆角响应

由图8可以看出，采用两阶段控制，在塔机启动和平稳运行阶段，吊绳摆角逐渐减小，在塔机开始制动后吊绳摆角能够迅速衰减，在10 s内，吊绳摆角基本上被消除。同时，由图9可知，臂架臂头水平加速度在整个工作过程中均较小。由于电流输入信号对应着变量泵排量，由图10可知，实际输入信号与操作者输入信号相比变化较小，在消摆的同时保证了变量泵工作在90%排量以上。由图11可以看出，在消摆的同时，变幅角度也能到达理想的位置。图12、图13表明，当绳长及臂长发生变化时，能达到同样的消摆效果，控制系统具有较好的鲁棒性。

5　结论

(1)控制器的控制算法对系统模型的依赖性较小，所以能够很好地满足系统非线性、变参数的控制要求，具有较好的鲁棒性。控制器的控制算法较为简单，增加了在实际中应用的可能性。

(2)通过适当地选取两阶段的补偿系数，吊绳摆角在起重机制动前渐进减小，制动后迅速衰减。同时，在起重机作业过程中，臂架臂头水平加速度始终小于0.6 m/s2，变量泵排量利用率在90%以上。

(3)在控制吊绳摆角的同时，位置控制器的设计保证了变幅角度的准确性。

[1]Sorensen K L, Singhose W, Dickerson S. A Controller Enabling Precise Positioning and Sway Reduction in Bridge and Gantry Cranes[J]. Contr. Eng. Pract., 2007, 15: 825-837.

[2]Blackburn D, Singhose W. Command Shaping for Nonlinear Crane Dynamics[J]. Journal of Vibration and Control, 2010, 16(4): 477-501.

[3]Hu G S, Ong C J,Teo C L. Minimum-time Control of a Crane with Simultaneous Traverse and Hoisting Motions[J]. Journal of Optimization Theory and Applications 2004, 120(2): 395-416.

[4]Wang Z, Surgenor B W. A Problem with the LQ Control of Overhead Cranes[J]. Trans. ASME J. Dynam. Syst. Measur. Control, 2006, 128(2): 436-440.

[5]Hua Y J, Shine Y K. Adaptive Coupling Control for Overhead Crane Systems[J]. Mechatronics, 2007,17: 143-152.

[6]Benhidjeb A,Gissinger G L. Fuzzy Control of an Overhead Crane Performance Comparision with Classic Control[J]. Control Engineering Practice, 1995, 3(12): 1687-1696.

[7]Hua Y J, Shine Y K.Adaptive Coupling Control for Overhead Crane Systems[J]. Mechatronics, 2007, 17: 143-152.

[8]王晓军.基于时滞滤波器的桥式卸船机的定位和防摆控制研究[D]. 上海: 上海交通大学, 2006.

[9]Kazuo K, Hiroyuki S,Toru Y. Variable Gain PD Sway Control of a Lifted Load for a Mobile Crane[C]//Proceedings of the American Control Conference. Arlington, VA: IEEE Press, 2001:953-958.

[10]卢长耿,李金良. 液压控制系统的分析与设计[M]. 北京: 煤炭工业出版社, 1991.

[11]国家技术监督局. GB/T 13752-1992 塔式起重机设计规范[S]. 北京: 中国标准出版社, 1993.

(编辑王艳丽)

Load Anti-sway Control of Luffing Motion for Cranes

Cao Xuyang1Yuan Jing2Li Wanli3Ding Chong4

1.Dalian University of Technology,Dalian,Liaoning,116024 2.YTO Group Corporation,Luoyang,Henan,471039 3.Dalian Yiliya Construction Machinery Co., Ltd.,Dalian,Liaoning,116024 4.Dalian Shipbuilding Industry Co., Ltd.,Dalian,Liaoning,116024

Aiming at the problems of poor precision, low operation efficiency and low security due to the load oscillation of luffing motion for crane,an error asymptotic compensation control method was proposed to minimize the sway angle of load. Based on the analysis of error asymptotic compensation control theory, the error asymptotic compensation controller was designed. Through appropriate adjustments to the two stage compensation coefficients, the sway angle of the lifted load was gradually decreased, meanwhile, the requirements of the acceleration and the pump displacement were met. The MATLAB simulation results show that error asymptotic compensation controller has good robustness and control precision for different ropes and jib lengths. After the crane began to brake, the sway angle is reduced to below 0.003 rad in 10 seconds.

crane; luffing motion; load oscillation; error asymptotic compensation controller

2014-03-06

工业信息化部高技术船舶科研项目

TH21; TP273DOI：10.3969/j.issn.1004-132X.2015.05.007

曹旭阳，男，1974年生。大连理工大学机械工程学院副教授。主要研究方向为机械机构优化设计、工程机械三维仿真及虚拟样机技术、电液控制技术。发表论文40余篇。袁靖，男，1983年生。中国一拖集团有限公司技术中心工程师。李万里，男，1984年生。大连益利亚工程机械有限公司工程师。丁冲，男，1969年生。大连船舶重工集团有限公司高级工程师。