基于Pareto优化的离散自由搜索算法求解多目标柔性作业车间调度问题

彭建刚　刘明周　张　玺　张铭鑫　葛茂根

合肥工业大学,合肥,230009

基于Pareto优化的离散自由搜索算法求解多目标柔性作业车间调度问题

彭建刚刘明周张玺张铭鑫葛茂根

合肥工业大学,合肥,230009

针对多目标柔性作业车间调度问题搜索空间的离散性和求解算法的收敛性，提出一种基于Pareto优化的离散自由搜索算法来求解多目标柔性作业车间调度问题。在建立基于Markov链数学模型的基础上，证明了算法以概率1收敛；引入首达最优解期望时间来分析算法收敛速度，并分析了算法时间复杂度。采用基于工序排序和机器分配的个体表达方式，在多目标柔性作业车间离散域，利用自由搜索算法在邻域小步幅精确搜索和在全局空间大步幅勘测进行寻优；通过自由搜索算法自适应赋予个体各异辨别能力和Pareto优化概念来比较个体优劣性，不仅保留优化个体，而且使个体寻优方向沿多目标柔性作业车间调度问题Pareto前沿逼近。通过对搜索过程中产生的伪调度方案进行可行性判定，以确保调度方案可行。采用10×10FJSP和8×8FJSP问题的实例进行寻优测试，验证了所提算法的可行性和有效性。

多目标柔性作业车间调度问题；自由搜索；Markov链；Pareto优化

0　引言

柔性作业车间问题(flexible job-shop scheduling problem, FJSP)突破了经典作业车间调度问题(job-shop scheduling problem,JSP)的资源唯一性约束，是复杂的NP-hard问题[1]，FJSP比JSP更适应现实制造车间的调度需求。实际生产调度往往需要满足多个相互冲突的目标，因此，大量生产调度属于多目标优化问题，寻求多方利益的合理折中成为生产调度决策的重要问题[2]。多目标柔性作业车间调度(multi-objective FJSP, MOFJSP)是面向多个目标进行优化与决策的FJSP，是实现先进制造技术的基础和关键，对MOFJSP问题的深入研究具有重要的理论意义和应用价值。

目前，求解MOFJSP的方法主要有进化算法和群智能优化算法。鞠全勇等[2]研究批量生产中以生产周期、最大提前/最大拖后时间、生产成本以及设备利用率指标为调度目标的FJSP优化调度问题，结合多种群粒子群搜索与遗传算法优点提出了具有倾向性粒子群搜索的多种群混合算法，提高了搜索效率和搜索质量。张超勇等[3]采用多目标进化算法解决具有工件释放时间、工件目标差异的FJSP调度问题，设计改进的NSGA-Ⅱ算法求解MOFJSP的Pareto解集，并运用层次分析法选出最优妥协解。王云等[4]应用改进的强度Pareto进化算法求解以制造工期、加工成本及交货期为目标函数的MOFJSP问题，并利用模糊集合理论的方法得到Pareto解的优先选择序列和一个最优解。Kacem等[5]采用基于模糊进化的Pareto优化法求解MOFJSP，将优化解质量的多目标评价转化成一个单一的适应度函数，通过模糊控制规则动态地计算适应度函数权重，使进化算法搜索方向朝Pareto前沿逼近，得到Pareto非支配解集，并通过适应度函数各个目标值的下边界值来评价最优解质量。张静等[6]采用基于工序排序和机器分配的粒子表达方式直接在离散域进行位置更新，并通过Pareto支配的概念来比较粒子的优劣性, 提出了一种基于Pareto支配的混合粒子群优化算法求解MOFJSP问题。Li等[7]结合多种局部搜索方法，引入Pareto概念对种群进行快速非支配排序，提出了基于Pareto的离散蜂群算法求解MOFJSP问题。

从现有文献可以看出，MOFJSP问题的求解，既要选择性能优良的优化算法，也要适合在离散空间与高效的局部搜索方法相结合，以提高算法效率、防止算法过早收敛；还要针对多目标优化特点，采用基于Pareto概念对种群进行非支配排序，寻求MOFJSP问题的Pareto非支配解集。本文选择集成遗传算法优胜劣汰机制、蚁群算法信息素和个体观察范围理论、粒子群算法群体记忆功能等优点的自由搜索(free search, FS)算法搜索MOFJSP问题优化解。FS算法的研究相比遗传算法、蚁群算法和粒子群算法等起步较晚，尚未形成系统的分析方法和较好的数学基础，特别是利用有效的数学工具对算法的收敛性分析和收敛速度估计是亟待解决的课题。本文在分析FS算法及其结构基础上，将FS算法引入离散领域，结合Pareto优化技术，提出基于Pareto优化的离散自由搜索算法(discrete free search based on Pareto-optimality, P-DFS)求解MOFJSP问题；利用P-DFS算法对应随机过程的Markov链性质证明了所提算法的收敛性、估计了算法的收敛速度、分析了算法的时间复杂度；通过算例仿真和结果对比，验证了所提出算法的可行性和有效性。

1　MOFJSP数学模型

企业内部不同部门，诸如采购部门、销售部门、制造部门、生产部门等从自身利益考虑，对生产调度提出不同期望，因此，通过优化部门之间相互作用且相互冲突的期望目标，寻求各方利益的合理折中成为解决MOFJSP问题的关键。求解MOFJSP，即为对存在多个相互冲突目标的柔性作业车间调度方案进行优化与决策。为便于分析与研究, 调度过程作以下假设和约束：每个工件的各道工序只能按照事先给定的顺序加工；每个工件在t=0时刻都可以开始加工，所有机器在时间t=0时刻都可以使用；在给定的时间内，一台机器只能加工一道工序；一道工序只能在其前道工序加工完成后，才能从其候选机器集合中选择一台空闲机器加工。

本文针对n个工件在m台机器上加工的MOFJSP的最大完工时间、机器总负荷和单台机器最大负荷等3种性能指标进行优化。建立MOFJSP的数学模型如下：

(1)

式中，ci为工件Ji的完工时间；Cmax为最大完工时间；WT为机器总负荷；max(Wh)为单台机器最大负荷。

2　FS算法及其离散化

2.1FS算法基本原理

FS算法是Penev和Littlefair于2005年提出的一种源于高等群居动物的群聚进化算法[8]。FS算法通过个体在邻域附近多维连续空间的小步幅精确搜索和在全局空间的大步幅勘测两个搜索过程寻找目标函数的最优解。

FS算法结构由初始化、搜索过程和终止判定3个步骤组成。Penev等[8]的研究表明，FS在收敛速度上优于遗传算法，在求解约束优化问题上优于粒子群算法，在求解平板问题上优于差分进化算法。

2.2离散FS算法

目前，FS算法的研究主要集中在连续型问题上，即描述FS算法个体及其运动状态规律的量是连续的，在离散领域，FS算法的应用文献甚少；而MOFJSP调度是典型的组合优化问题，为了将FS算法用于求解MOFJSP，本文提出离散FS算法(discrete free search, DFS)。FS离散化的关键是根据MOFJSP问题领域定义个体寻优的位置更新规则。

2.2.1DFS的编码

DFS算法采用基于工序和机器分配相结合的编码方式进行编码，如图1所示。工件的每道工序Oij在可用设备集Mij⊆{1,2,…,m}中的一台设备上加工。第1条染色体编码表示的工序顺序为(O21,O11,O22,O31,O23,O12,O32),第2条染色体编码表示的机器序列为(M1,M2,M3,M2,M4, M4,M3)。

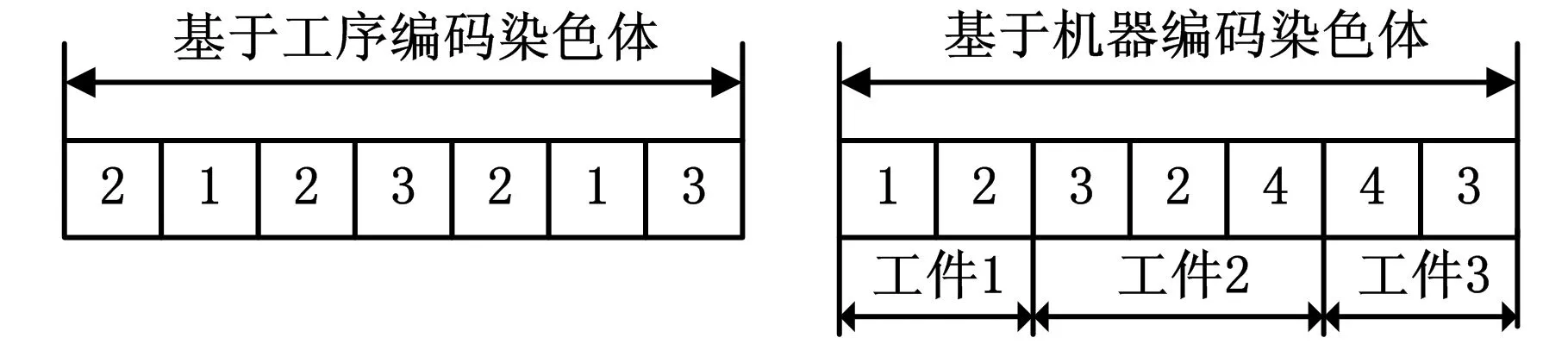
图1　基于工序和机器的编码

2.2.2个体位置更新

在FS算法搜索空间中，个体位置Xi=(x1,x2,…,xr)是一个r维向量，结合MOFJSP特点和文献[9]提出的位置更新策略，定义FS算法个体位置更新公式为

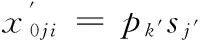
(1)个体从小步幅搜索获得的寻优信息如下：

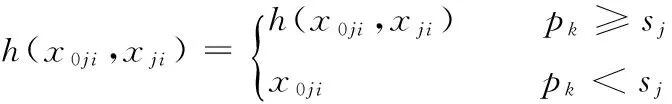
(3)调度方案可行性判定[10]。由于个体位置移动产生的调度方案不一定是可行调度方案，故需进行调度方案可行性甄别，其操作为

πk=πk-1⊕(j,d)k,k=1,2,…,r

σ+l=φ(πk)

式中，⊕为第j个个体经移动d位置后产生调度方案πk的操作算子；σ为调度方案；l为调度方案中个体移动前后的位置差；φ为工件序列修正程序。

即在新调度方案中，扫描工件排列，若某一位置分配多个工件，则结合FIFO(first-in-first-out)规则、工序约束和机器约束将多余工件向后移动到最近的空位上；若某位置为空，则同样结合FIFO规则、工序约束和机器约束从其后面最近的含有多个工件的位置上提取一个工件插入；最终得到可行调度方案。

3　P-DFS算法设计

3.1符号说明

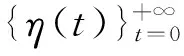
3.2P-DFS算法

MOFJSP面向FJSP的多个相互冲突目标实施调度方案优化与决策，是复杂组合优化问题。本文将FS算法引入离散领域，在实现FS离散化的基础上，结合求解多目标优化问题的Pareto优化技术，提出P-DFS算法求解MOFJSP问题。在MOFJSP离散域内，P-DFS算法个体在邻域附近多维空间作小步幅精确搜索，在全局空间作大步幅勘测，目的是寻找目标函数优化解。个体将自己在邻域空间发现的最优解以信息素的形式保存起来，并利用信息素和灵敏度选择下一步搜索的位置。信息素反映多目标函数解的质量；灵敏度犹如“过滤器”，不仅保留优良个体，而且对不良个体重新初始化。不同的个体有不同的灵敏度，同一个体在不同的搜索步中有不同的灵敏度，个体选择适合其灵敏度的信息素作为下一步搜索的起始点。每次随机迭代搜索到的优化解进入归档集，通过非支配排序得到非支配解，最终构成Pareto非支配解集[11]。因此，P-DFS算法不仅有利于提高算法种群质量，而且对寻优搜索方向朝Pareto前沿逼近有重要的导向作用。基于双目标P-DFS算法搜索方向如图2所示。

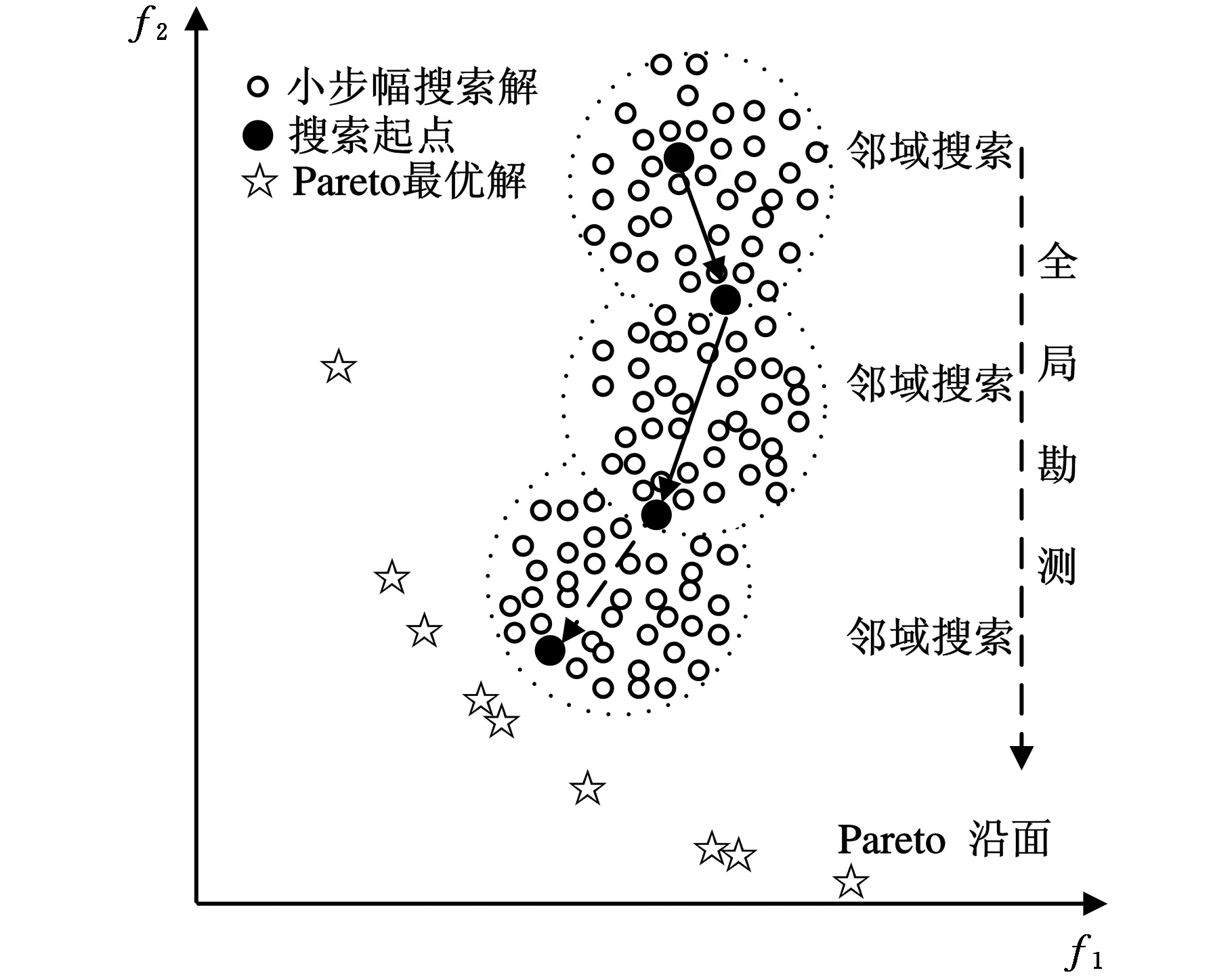
图2　基于双目标P-DFS算法搜索方向

3.3P-DFS算法步骤

(1)设定搜索初始值。设定种群规模N，搜索代数G，搜索小步幅数T，邻域半径Rji。

(2)种群初始化。随机产生初始种群{η(0)}，并计算个体适应值。

(3)根据Pareto支配关系，生成初始种群归档集A(0)=M({η(0)},⪯)。

(4)释放初始信息素pk→xjkp。

(5)计算灵敏度sj。

(7)计算搜索步个体适应值。

(8)生成迭代种群{η(t)}t≥0。

(9)种群个体非支配排序，生成新的归档集:

A(t+1)=Mf(A(t)∪{η(t)}t≥0,⪯)

(10)释放信息素pk→xjkp。

(11)终止判定。

4　P-DFS算法收敛性与收敛速度分析

4.1P-DFS算法的Markov链

P-DFS算法对应的寻优过程中，个体根据信息素和灵敏度进行随机搜索，信息素和灵敏度在不同搜索步中不断更新，第t次搜索信息素和灵敏度由第t-1次搜索的当前最优解和搜索得到的解集所决定。

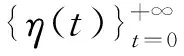
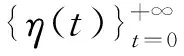
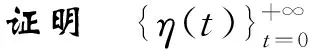
P(η(t)∈Y′|η(0),η(1),…,η(t-1))=

P(η(t)∈Y′|η(t-1))Y′⊆Y

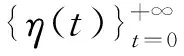
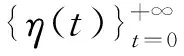
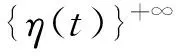
证毕。

4.2P-DFS算法的收敛性分析

定义2[11]P-DFS算法搜索到的Pareto非支配解构成的集合为Pareto非支配解集，记为M(F,⪯)，即

M(F,⪯)={x*|┐∃x∈F:xx*}

Pareto非支配解集对应的状态空间称为最优状态空间，记为Y*。

定义3[13]设A、B是有限基础集X的子集，则d(A,B)=|A∪B|-|A∩B|是X的幂集距离。

定义4[12]若Markov链转移概率与初始时刻无关，则称Markov链为齐次的。

从有互联网以来的历史我们发现，不能仅仅只依赖互联网本身达成商业价值的创造。我们不能忽视其他行业与互联网行业的相互补足。如此才能更多地发现企业的更优发展模式。

定义5[14]随机过程从一个状态经过有限步转移到达另一状态的条件概率大于0，则称随机过程的转移矩阵是不可约的。

引理1[14]齐次有限状态的离散时间参数Markov链的概率特性主要由一步转移矩阵决定。

引理2[13]无论初始分布如何，一个具有有限状态空间和不可约转移矩阵的齐次Markov链经常以概率1无穷多次地访问每个状态。

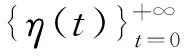
证明方法参见文献[13]。

定理3P-DFS算法对应的Markov链以概率1收敛到Pareto非支配解集。

证明P-DFS算法状态空间YX的状态有限性决定了P-DFS算法对应的随机过程是有限Markov链；P-DFS算法步骤(2)、步骤(6)解释了转移概率与初始状态无关，决定了P-DFS算法对应的Markov链是齐次的；P-DFS算法步骤(5)～步骤(9)决定了其转移矩阵是不可约的，由定义5和引理1可得：P-DFS算法对应的Markov链是不可约的。根据定理2，当t→∞时,d(f(η(t),F*)以概率1趋于0成立，由定义3可得：P-DFS算法对应的Markov链以概率1收敛到最优解集F*。由引理2可得：P-DFS算法对应的Markov链的每一个最优解将以概率1搜索到，并经过P-DFS算法步骤(9)非支配排序获得Pareto非支配解集，因此，P-DFS算法对应的Markov链以概率1收敛到Pareto非支配解集。

证毕。

4.3P-DFS算法的收敛速度分析

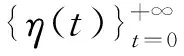
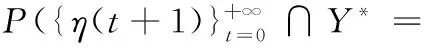
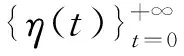
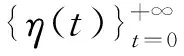
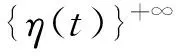
A(t+1)=Mf(A(t)∪{η(t)},⪯)

可得

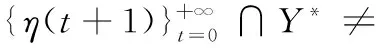
所以

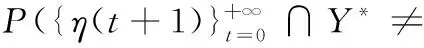
成立，即

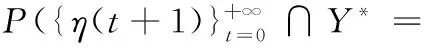
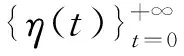
证毕。

P-DFS算法对应的随机过程满足吸收态Markov性，引入首达最优解期望时间(expected first hitting time, EFHT)[16]表征P-DFS算法的收敛速度。

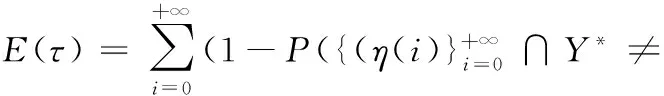
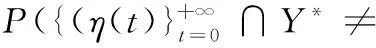
可得

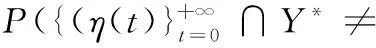
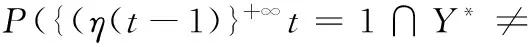
P(τ≤t)-P(τ≤t-1)

可得

∅)-

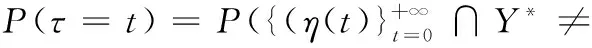
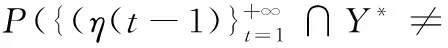
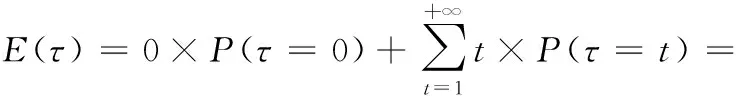
证毕。

4.4P-DFS算法复杂度分析

假设优化目标函数个数为r，种群规模为N。从3.3节算法步骤可以看出，P-DFS算法寻优主要由5部分组成：第1部分计算个体适应值，其时间复杂度约为O(rN)；第2部分与归档集中非支配个体比较，其时间复杂度为O(rN2)；第3部分计算灵敏度，其时间复杂度约为O(rN)；第4部分选择新的搜索起点，其时间复杂度约为O(rN)，第5部分为个体小步幅搜索和大步幅勘测，其时间复杂度为O(rN)。因此，P-DFS算法的总时间复杂度为

O(r,N)=[O(rN)+O(rN2)+O(rN)+

O(rN)+O(rN)]≈O(rN2)

P-DFS算法的时间复杂度与个体规模、优化目标函数个数有关，与基于Pareto非支配排序[17]的时间复杂度相同。

5　P-DFS算法实验结果与比较

为验证算法寻优性能，采用文献[18]提供的10×10和8×8FJSP问题实例进行寻优测试。算法采用MATLABR2009a编程语言实现，微机运行环境为：CPUE6500，主频2.93GHz，内存2G；搜索初始值设定为：种群规模N=50,搜索代数G=100,搜索小步幅数T=50,邻域半径Rji=2。P-DFS算法的流程如图3所示。

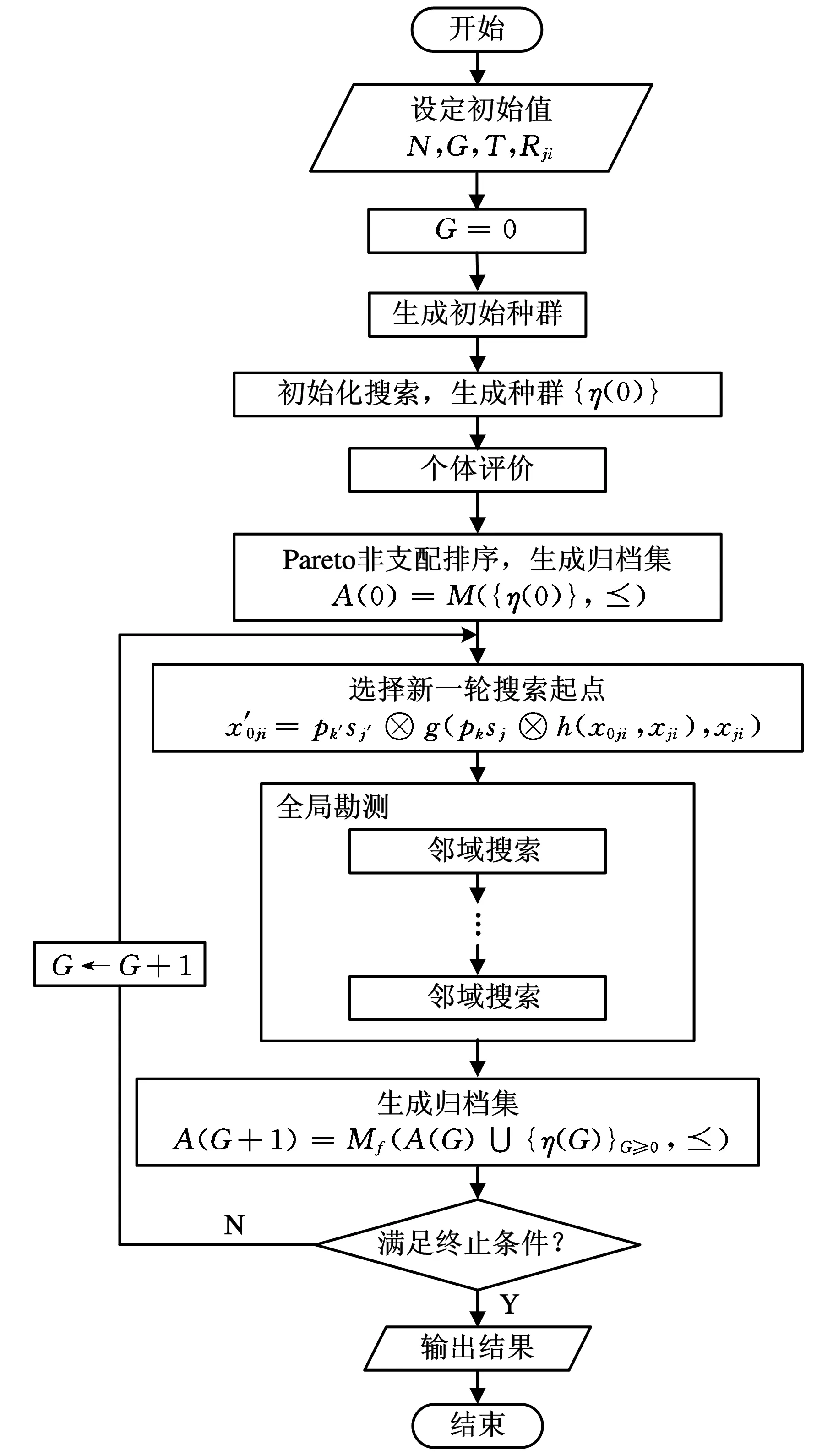
图3　P-DFS算法流程图

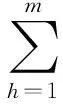
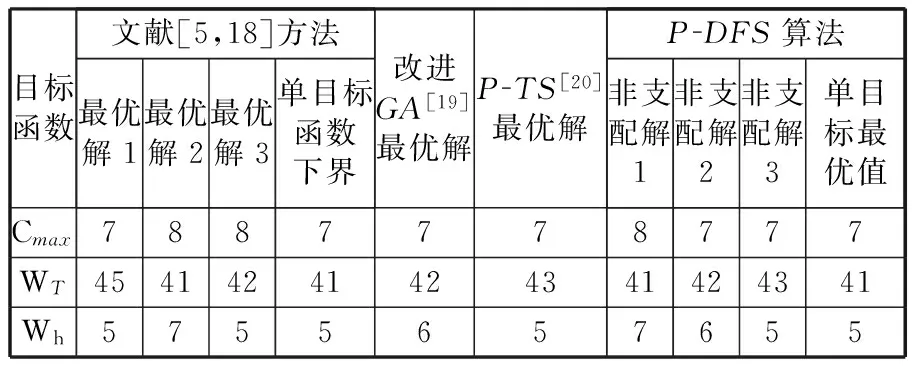
表1　10×10 FJSP问题的结果比较

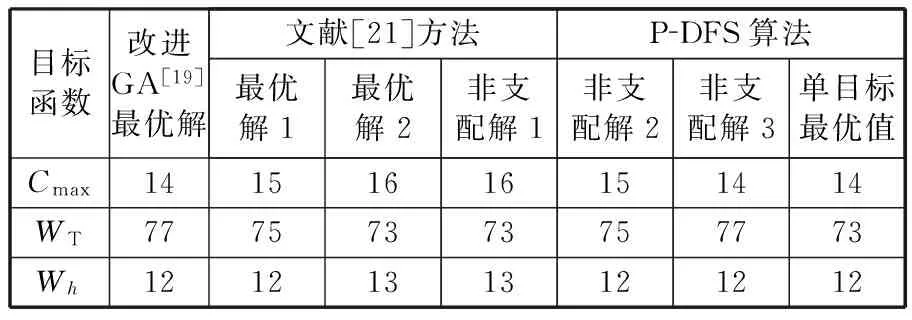
表2　8×8 FJSP问题的结果比较

从表1和表2结果可以看出，对于10×10 FJSP和8×8 FJSP问题实例，分别运行P-DFS算法获得的3个非支配解总体上不劣于文献算法给出的最优解(文献结果统称为最优解)。单目标函数值下界是衡量算法局部搜索能力的重要体现，针对本文实例，P-DFS算法搜索到了两个实例所有单目标函数值下界，并求解到相应的Pareto非支配解集。因此，采用P-DFS算法求解10×10 FJSP问题和8×8 FJSP问题不仅可行而且效果良好。

6　结论

(1)针对MOFJSP问题特点，将FS算法引入离散领域，在定义算法个体位置更新和判定调度方案可行基础上，结合Pareto优化提出了P-DFS算法。在MOFJSP离散域内，通过DFS算法小步幅精确搜索和全局空间的大步幅勘测，以及最优解的非支配排序，使算法种群的寻优方向朝Pareto前沿逼近，最终求解MOFJSP问题的最优可行解。

(2)利用P-DFS算法的Markov链性质，证明P-DFS算法以概率1收敛到Pareto非支配解集；引入首达最优解期望时间和吸收态Markov链性质分析P-DFS算法收敛速度；从P-DFS算法的主要寻优过程分析其时间复杂度。

(3)基于P-DFS算法收敛性证明和收敛速度分析结论，将其应用于MOFJSP问题求解；采用相同的实例进行实验测试，并将P-DFS算法的寻优结果与文献结果进行比较，验证了P-DFS算法的可行性和有效性。

[1]Blazewicz J,Finke G,Haopt G.New Trends in Machine Scheduling[J].European Journal of Operational Research,1988, 37: 303-317.

[2]鞠全勇,朱剑英.多目标批量生产柔性作业车间优化调度[J].机械工程学报,2007,43(8):148-154.

Ju Quanyong,Zhu Jianying.Multi-objective Flexible Job Shop Scheduling of Batch Production[J].Chinese Journal of Mechanical,2007,43(8):148-154.

[3]张超勇,董星,王晓娟,等.基于改进非支配排序遗传算法的多目标柔性作业车间调度[J].机械工程学报, 2010,46(11):156- 164.

Zhang Chaoyong,Dong Xing,Wang Xiaojuan, et al. Improved NSGA-Ⅱ for the Multi-objective Flexible Job-shop Scheduling Problem[J].Journal of Mechanical Engineering, 2010, 46(11): 156-164.

[4]王云,谭建荣,冯毅雄,等.基于SPEA的多目标柔性作业车间调度方法[J].中国机械工程,2010, 21(10):1167-1172.

Wang Yun,Tan Jianrong,Feng Yixiong, et al. Multi-objective Flexible Job-shop Scheduling Based on Strength Pareto Evolutionary Algorithm[J]. China Mechanical Engineering, 2010, 21(10):1167-1172.

[5]Kacem I, Hammadi S, Borne P.Pareto-optimality Approach for Flexible Job-shop Scheduling Problems: Hybridization of Evolutionary Algorithms and Fuzzy Logic[J]. Mathematics and Computers in Simulation, 2002,60: 245- 276.

[6]张静,王万良,徐新黎,等.混合粒子群算法求解多目标柔性作业车间调度问题[J].控制理论与应用,2012,29 (6): 715-722.

Zhang Jing,Wang Wanliang,Xu Xinli,et al.Hybrid Particle-swarm Optimization for Multi-objective Flexible Job-shop Scheduling Problem[J].Control Theory & Applications,2012, 29(6):715-722.

[7]Li Junqing, Pan Quanke, Gao Kaizhou. Pareto-based Discrete Artificial Bee Colony Algorithm for Multi-objective Flexible Job Shop Scheduling Problems[J]. International Journal of Advanced Manufacturing Technology, 2011, 55: 1159-1169.

[8]Penev K, Littlefair G. Free Search-a Comparative Analysis[J]. Information Sciences,2005,172(1/2):173-193.

[9]潘全科,王文宏,朱剑英,等.基于粒子群优化和变邻域搜索的混合调度算法[J].计算机集成制造系统, 2007,13(2): 323- 328.

Pan Quanke, Wang Wenhong, Zhu Jianying, et al.Hybrid Heuristics Based on Particle Swarm Optimization and Variable Neighborhood Search for Job Shop Scheduling[J].Computer Integrated Manufacturing Systems, 2007,13(2):323-328.

[10]Anghinolfi D,Paolucci M.A New Discrete Particle Swarm Optimization Approach for the Single-machine Total Weighted Tardiness Scheduling Problem with Sequence- dependent Setup Times[J]. European Journal of Operational Research, 2009, 193:73-85.

[11]公茂果,焦李成,杨咚咚,等.进化多目标优化算法研究[J].软件学报, 2009,20(2):271-289.

Gong Maoguo,Jiao Licheng,Yang Dongdong,et al.Research on Evolutionary Multi-objective Optimization Algorithms[J]. Journal of Software, 2009, 20(2): 271-289.

[12]张文修,梁怡.遗传算法的数学基础[M].西安:西安交通大学出版社,2000.

[13]Rudolph G, Agapie A.Convergence Properties of Some Multi-objective Evolutionary Algorithms[C]//Proceedings of on IEEE Conference Evolutionary Computation.Piscataway, New Jersey, 2000:1010-1016.

[14]胡迪鹤.随机环境中的马尔可夫过程[M].北京:高等教育出版社,2011.

[15]黄翰,郝志峰,吴春国,等.蚁群算法的收敛速度分析[J].计算机学报,2007,30(8): 1344-1353.

Huang Han,Hao Zhifeng,Wu Chunguo,et al. The Convergence Speed of Ant Colony Optimization[J]. Chinese Journal of Computers, 2007,30(8):1344-1353.

[16]Yu Yang,Zhou Zhihua.A New Approach to Estimating the Expected First Hitting Time of Evolutionary Algorithms[J]. Artificial Intelligence,2008,172:1809-1832.

[17]Deb K, Pratap A, Agarwal S, et al. A Fast and Elitist Multi- objective Genetic Algorithms:NSGA-Ⅱ[J].IEEE Trans.on Evolutionary Computation,2002,6(2):182-197.

[18]Kacem I,Hammadi S,Borne P.Approach by Localization and Multi-objective Evolutionary Optimization for Flexible Job-shop Scheduling Problems[J].IEEE Transaction Systems, Man,and Cybernetics-Part C,Applications and Reviews, 2002, 32(1):1-13.

[19]张国辉,高亮,李培根,等.改进遗传算法求解柔性作业车间调度问题[J].机械工程学报,2009,45(7):145-151.

Zhang Guohui,Gao Liang,Li Peigen, et al. Improved Genetic Algorithm for the Flexible Job-shop Scheduling Problem[J]. Journal of Mechanical Engineering, 2009, 45(7): 145-151.

[20]李俊青,潘全科,王玉亭.多目标柔性车间调度的Pareto混合禁忌搜索算法[J].计算机集成制造系统, 2010,16(7): 1419- 1426.

Li Junqing,Pan Quanke,Wang Yuting. Hybrid Pareto-based Tabu Search Algorithm for Solving the Multi-objective Flexible Job Shop Scheduling Problem[J].Computer Integrated Manufacturing Systems, 2010,16(7):1419-1426.

[21]Xia Weijun, Wu Zhiming.An Effective Hybrid Optimization Approach for Multi-objective Flexible Job-shop Scheduling Problems[J].Computers & Industrial Engineering,2005,48: 409-425.

(编辑王艳丽)

Discrete Free Search Based on Pareto-optimality for Multi-objective Flexible Job-shop Scheduling Problem

Peng JiangangLiu MingzhouZhang XiZhang MingxinGe Maogen

Hefei University of Technology,Hefei,230009

A discrete free search algorithm based on Pareto-optimality was proposed for solving multi-objective flexible job-shop scheduling problem. The convergence with probability one of the proposed algorithm was demonstrated based on Markov chain and the convergence rate was analyzed based on expected first hitting time. The computational complexity of algorithm was also analyzed. Individuals of algorithm were represented based on job operation and machine assignment, and updated either with small precise steps for local search or with large steps for global exploration in discrete domain. The individuals were compared through adaptive sensibility and Pareto-optimality concept. The proposed algorithm was to retain the optimization individuals, and to guide individuals taking exploration walks towards Pareto-optimality front of multi-objective flexible job-shop scheduling problem. The feasibility and effectiveness of the proposed algorithm were verified by both 10×10FJSP and 8×8FJSP instance.

multi-objective flexible job-shop scheduling problem；free search；Markov chain；Pareto-optimality

2013-12-24

国家自然科学基金资助项目(71071046)

TH186DOI：10.3969/j.issn.1004-132X.2015.05.009

彭建刚，男，1970年生。合肥工业大学机械与汽车工程学院博士研究生、汽车工程技术研究院副研究员。主要研究方向为生产计划与调度，先进制造技术和多目标优化算法。刘明周，男，1968年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。张玺，男，1985年生。合肥工业大学机械与汽车工程学院博士研究生。张铭鑫，男，1980年生。合肥工业大学机械与汽车工程学院讲师。葛茂根，男，1979年生。合肥工业大学机械与汽车工程学院副教授。