分子力对机电耦合薄膜压力敏感元件振动的影响

孙丽波，许立忠，丁 玲

（1.燕山大学环境与化学工程学院，河北秦皇岛066004；2.燕山大学机械工程学院，河北秦皇岛066004；3.燕山大学信息科学与工程学院，河北秦皇岛066004）

分子力对机电耦合薄膜压力敏感元件振动的影响

孙丽波1，许立忠2，*，丁 玲3

（1.燕山大学环境与化学工程学院，河北秦皇岛066004；2.燕山大学机械工程学院，河北秦皇岛066004；3.燕山大学信息科学与工程学院，河北秦皇岛066004）

本文将薄膜式微谐振压力传感器谐振子简化为对边简支对边自由机电耦合微薄膜谐振系统，给出了考虑分子力作用时微薄膜压力敏感元件机电耦合系统动力学方程，推导其振型方程及频率方程，研究了分子力对系统固有频率及自由振动的影响规律。结果表明：分子力对于机电耦合微薄膜的自由振动固有频率具有重要的影响。随着系统初始间隙的减小、工作电压的增大、微薄膜厚度的减小以及薄膜长度的增大，分子力对系统固有频率的影响更加显著。在低阶模态下，分子力对固有频率的影响变大，应该予以考虑。当初始间隙减小到0.1μm时，Casimir力对固有频率的影响比van der Waals力明显，必须考虑Casimir力的影响。论文有助于薄膜式微谐振压力传感器谐振子的动力学理论分析，研究结果对于MEMS压力传感器进一步小型化具有指导意义。关键词：对边简支对边自由；机电耦合；微薄膜；van der Waals力；Casimir力；MEMS

0　引言

微谐振式压力传感器具有直接输出数字信号、体积小、功耗低、响应快、灵敏度高、易于集成以及耐恶劣工作环境等优势，被成功应用于航空航天、疾病诊断、气象、石化等领域，已成为国内外微机电系统（micro-electromechanical systems，MEMS）领域中一个重要研究方向［1］。微谐振压力传感器多为微梁式和微薄膜式两种结构，其中薄膜式微谐振压力传感器输出的测试信号较强，对测试电路的要求较低，更符合传感器集成化、微型化的发展方向［2-3］。

近年来，国内外学者对微谐振压力传感器谐振子的振动特性进行了大量的研究。1993年Alonso等人对NiCr薄膜微谐振式压力传感器谐振子的振动特性及灵敏度的影响因素进行了理论分析［4］；2006年樊尚春等人对微谐振式压力传感器的非线性振动进行了研究，利用多尺度法求解出非线性项对传感器固有频率的影响规律［5］；2007年叶湘滨等人对谐振式压力传感器的灵敏度进行了理论分析［6］；2007年丁建宁等人对MEMS中薄膜结构在Casimir力作用下的粘附问题进行了研究，结果表明Casimir力在微纳尺度下的影响不可忽略［7］；2012年许立忠等人对谐振式压力传感器振动特性进行了分析，完成了谐振子多场耦合系统动力学研究［8］。

在微谐振压力传感器系统中，静电力对谐振子的动力学行为具有决定性作用，然而随着系统尺寸、间隙进一步减小到微米、纳米量级，微构件间的分子力（van der Waals和Casimir力）作用变得越来越明显。2003年赵亚溥等人研究了分子力作用下纳米致动器吸合动力学的稳定性问题，提出了仅考虑分子力作用时，纳米致动器吸合的同宿轨道分岔和分离长度［9］，并在其著作中对分子间力进行了明确而深入地说明。Casimir力和van der Waals力既有联系也有区别。它们在本质上都和电磁场的波动效应有关，van der Waals力和距离的三次方相关，Casimir力和距离的四次方相关，Casimir力比van der Waals力更长程。当两个介电物体间的距离远小于c/ω0（c是光速，ω0是电解质的基频，且c/ω0≈5～100 nm）时，van der Waals力起主导作用；当两个介电物体的距离大于c/ω0而小于λT（λT是温度T=300 K时，光子的de Broglie波长）时，Casimir效应起主导作用［10］。微谐振压力传感器以谐振子的固有频率变化量来测量外界压力的大小，谐振子的振动特性直接影响传感器的工作性能，将薄膜式微谐振压力传感器谐振子简化为机电耦合微薄膜谐振系统，研究其在分子力作用下振动特性为该种传感器的动力学优化设计提供理论依据。

1　动力学方程

薄膜式微谐振压力传感器多为静电驱动，谐振子通常采用方形膜片，可将其简化为静电场力和分子力作用下的微薄膜机电耦合系统（如图1所示），系统由上层的矩形微薄膜、下层固定的刚性基板以及电系统构成，微薄膜长度和宽度分别为a、b。系统在均布静电场力的作用下微薄膜与刚性基板相互吸引，微薄膜相对于刚性基板产生位移，实现致动，同时，整个微薄膜上作用有分布的分子力。以微薄膜中面上矩形微元dxdy代替微元体δdxdy表示微元受力情况，q（x，y，t）是分布在单位面积上的外力，包括静电场力和分子力，即q=qe+qn，qe表示单位面积静电场力，当n=2时，分子力为van der Waals力q2，当n=3时，分子力为Casimir力q3，忽略惯性力矩。

图1　微薄膜机电耦合结构模型Fig.1 Structure model of electromechanical coupling thin film

为了对微薄膜振动响应特性进行求解，将微薄膜沿z轴方向的位移、电容、电压、电场力、分子力分解为静态和动态两部分：

式中，具有下标0的项表示该物理量的静态部分，带有前缀Δ的项表示该物理量的动态部分。w为微薄膜沿z轴方向的位移，U、C分别为微薄膜与刚性基板之间工作电压、电容。分别将静电场力和分子力对动态间隙求导，并在静态位移处展开成泰勒级数，根据文献［11］机电动力学理论，微薄膜单位面积动态电场力大小为

式中，t0为微薄膜与刚性基板之间的静态初始间隙（mm），ε0为真空介电常数。

单位面积动态van der Waals力大小为

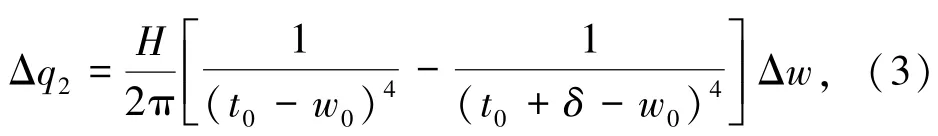
单位面积动态Casimir力大小为

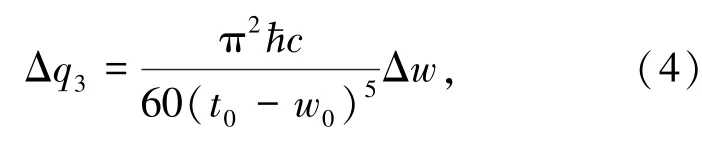
式中，H为汉马克（Hamaker）常数，取值范围一般在（0.4～4）×10-19J。ћ=h*/2π，h*为普朗克（Planck）常数，ћ=1.055×10-34J·s，c为光速，c=2.998×108m/s。

以各向同性、匀质、等厚度矩形微薄膜为研究对象，根据振动力学理论推导直角坐标系下微薄膜机电耦合系统在静电场力及分子力作用下系统总体动力学方程：

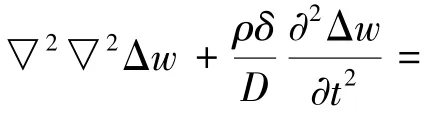
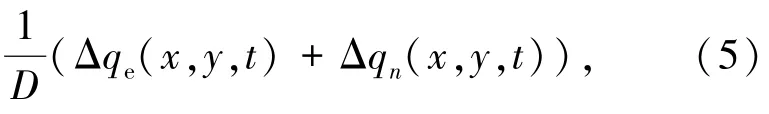
式中，δ、ρ分别为微薄膜厚度和材料密度，D为抗弯刚度，D=Eδ3/12（1-μ2），E为弹性模量，μ为泊松比。▽2▽2=∂4/∂x4+2∂4/∂x2∂y2+∂4/∂y4为重调和算子。

当只有静电场力作用时，系统动力学方程为

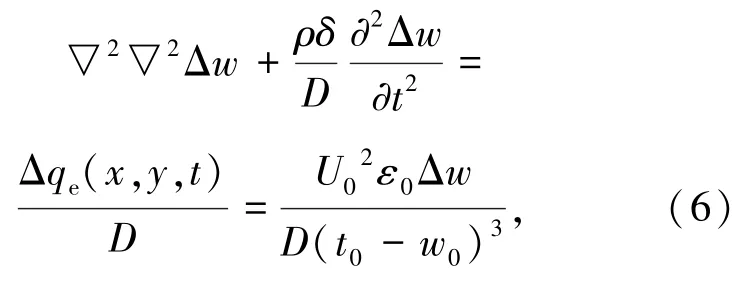
当考虑静电场力和van der Waals力时，n=2，系统动力学方程为

当考虑静电场力和Casimir力时，n=3，系统动力学方程为

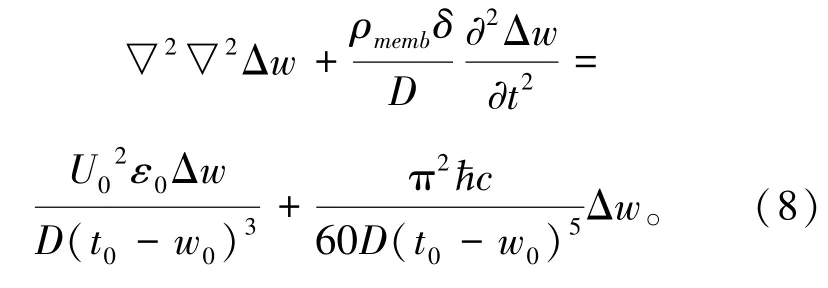
2　自由振动响应求解

选取对边简支对边自由边界条件的谐振薄膜为研究对象，考虑分子力影响下微薄膜机电耦合系统，建立直角坐标系如图2所示。x=0和x=a为两简支边，y=0和y=b为两自由边。

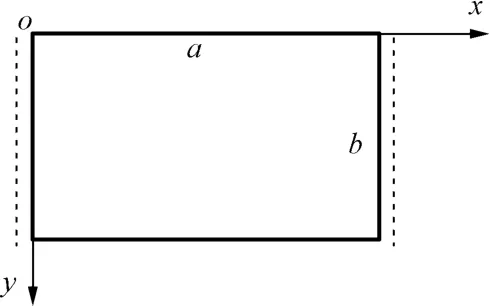
图2　对边简支对边自由微薄膜直角坐标系Fig.2 Coordinate system of thin film with two opposite edges simply supported and other two free

根据文献［12-13］振动理论采用分离变量法求解动态弯曲振动方程，设Δw=ΔW（x，y）· sin（ωt+φ），将其代入式（5）得总体振型方程：

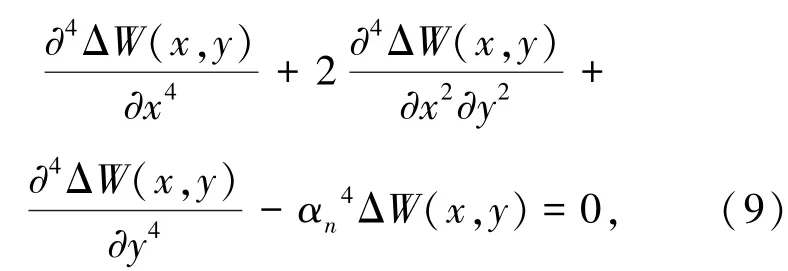
当只有静电场力作用时，取n=e

当考虑静电场力和van der Waals力时，取n=2：

当考虑静电场力和Casimir力时，取n=3：

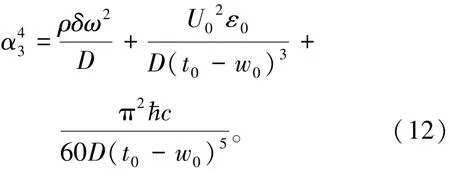
取满足对边简支对边自由边界条件的振型函数：

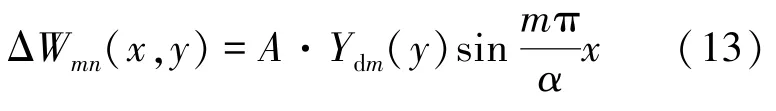
式中，Ydm为y的未知函数，A为常数。将振型函数式（13）代入总体振型方程，并设Ydm=eβmy，求解特征方程的一般解，进而得到振型表达式

其中，

将y=0和y=b两自由边边界条件代入振型表达式可得关于Adm、Bdm、Cdm、Ddm4个待定系数的齐次线性方程组，根据方程组有非零解的条件可得考虑分子力作用下对边简支对边自由微薄膜机电耦合系统频率方程：

上式是一个关于频率的超越方程，解此超越方程，可得各阶频率ωmn。对应每个频率可以求得特征向量（AdmnBdmnCdmnDdmn）T，将其代回式（14）可得第（m，n）阶振型

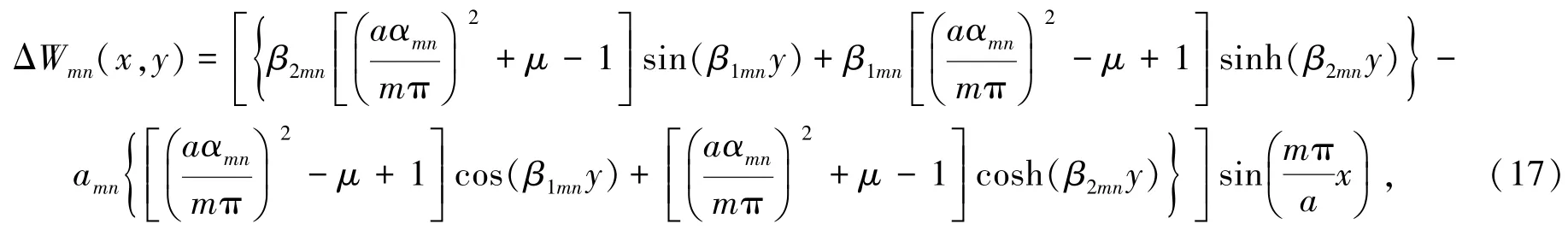
其中，αmn为式（15）中每个β1m，β2m所对应的αn值，amn表达式为

3　算例分析

选取硅材料制成的方形膜片，系统物理参数如表1所示。

微薄膜机电耦合系统自由振动低阶主振型如图3所示，工作电压U0=0.5 v，初始间隙t0=0.2 μm。只考虑静电场力作用时的主振型记为ΔWmne（n=e），考虑静电场力和van der Waals力作用时的主振型记为ΔWmn2（n=2），考虑静电场力和Casimir力作用时的主振型记为ΔWmn3（n=3）。由于篇幅所限，仅给出第一阶主振型。

表1　系统物理参数Tab.1 Parameters of system

由图3可知：

1）由于对边简支对边自由微薄膜的边界条件和材料几何尺寸都具有对称性，其主振型也具有对称性，由于静电场力和分子力的作用，微薄膜上各点同相振动。x=0和x=a为两简支边，y=0和y=b为两自由边。简支边较刚而自由边最柔，自由边振动幅值最大。

2）只考虑静电场力作用，考虑静电场力加van der Waals力作用，考虑静电场力加Casimir力作用3种情况下系统主振型模态均呈现周期性变化规律，同时考虑静电场力和分子力作用时响应振幅大于仅仅考虑静电场力作用时的响应振幅，而考虑静电场力加van der Waals力作用时响应振幅差值大于考虑静电场力加Casimir力作用的振幅差值。说明van der Waals力和Casimir力对振动模态产生了不同程度的影响，在进行传感器谐振敏感元件的动力学设计时，应该考虑分子力的影响以及两种分子力的不同作用效果，否则将产生较大误差。

前三阶固有频率及频率差ωe-ωn随系统初始间隙、工作电压、微薄膜厚度、微薄膜长度的变化规律，如表2～9所示，由于用作谐振敏感元件的方形膜片只工作在低阶频率，故本文研究的具体算例只限于前两阶。只考虑静电场力作用时的固有频率记为ωe（n=e），考虑静电场力和van der Waals力作用时的固有频率记为ω2（n=2），考虑静电场力和Casimir力作用时的固有频率记为ω3（n=3）。

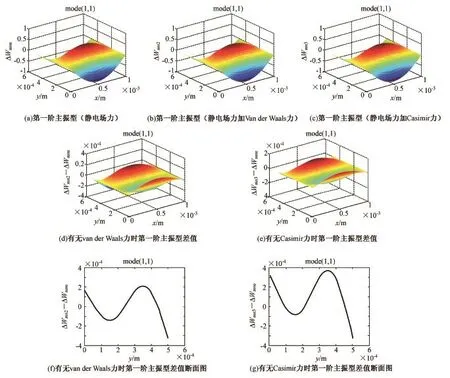
图3　主振型Fig.3 Main vibration modes

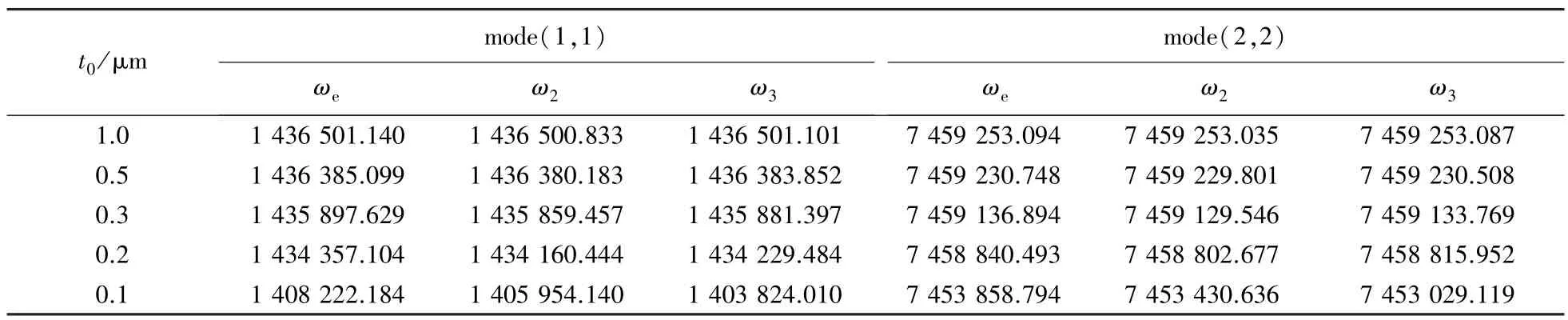
表2　固有频率随初始间隙的变化规律Tab.2 Changes of natural frequencies with initial gaps rad/s

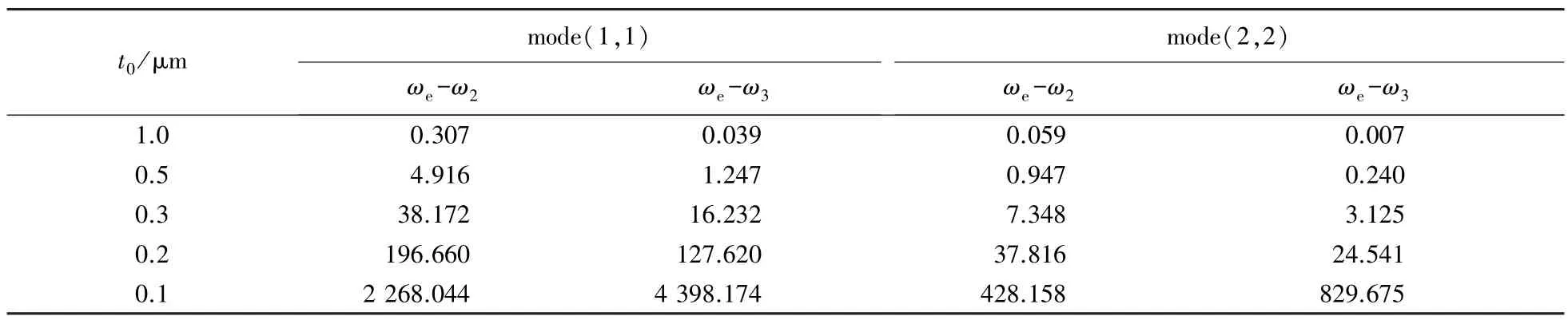
表3　频率差ωe-ωn随初始间隙的变化规律Tab.3 Change of frequency differences ωe-ωnwith initial gaps rad/s

表4　固有频率随工作电压的变化规律Tab.4 Changes of natural frequencies with working voltages rad/s

表5　频率差ωe-ωn随工作电压的变化规律Tab.5 Changes of frequency differences ωe-ωnwith working voltages rad/s

表6　固有频率随微薄膜厚度的变化规律Tab.6 Changes of natural frequencies with thicknesses rad/s

表7　频率差ωe-ωn随微薄膜厚度的变化规律Tab.7 Changes of frequency differences ωe-ωnwith thicknesses rad/s

表8　固有频率随微薄膜长度的变化规律Tab.8 Changes of natural frequencies with lengths rad/s

表9　频率差ωe-ωn随微薄膜长度的变化规律Tab.9 Changes of frequency differences ωe-ωnwith lengths rad/s

表2～9数据表明：

1）同时考虑静电场力和分子力作用的微薄膜各阶固有频率均小于只考虑静电场力作用的固有频率，说明考虑分子力作用，固有频率降低，ωe＞ωn（n=2，3），高阶模态下频率差小于低阶模态，说明低阶模态下分子力对固有频率的影响更加显著。

2）随着初始间隙的减小，固有频率ωn（n=e，2，3）均减小。这是因为随着初始间隙的减小，静电场力和分子力作用增大，导致耦合系统的刚度降低。当初始间隙t0＞0.2 μm时，ωe＞ω3＞ω2，同时考虑静电场力和Casimir力作用时的固有频率大于同时考虑静电场力和van der Waals力作用时的固有频率；而当初始间隙t0=0.1 μm时，ωe＞ω2＞ω3，同时考虑静电场力和Casimir力作用时的微薄膜固有频率又小于同时考虑静电场力和van der Waals力作用时的微薄膜固有频率，说明当初始间隙减小到0.1 μm时，Casimir力对固有频率的影响比van der Waals力更加明显。

3）当初始间隙较大时（t0＞0.3 μm），频率差ωe-ωn（n=2，3）不明显，频率差较小。当初始间隙较小时（t0≤0.2 μm），频率差明显，频率差增大，说明随着初始间隙的减小，分子力作用增强。当t0＞0.1 μm时，ωe-ω2均大于ωe-ω3，而当t0=0.1 μm时，ωe-ω3均大于ωe-ω2，说明当初始间隙t0≤0.1 μm时，Casimir力对固有频率的影响更加显著。

4）随着工作电压的减小，固有频率增大，而频率差ωe-ωn（n=2，3）减小，这表明随着工作电压值的减小，分子力对固有频率的影响减小，这是由于工作电压值减小，微薄膜与刚性基底间的电场强度降低，导致微薄膜弹性变形减小，进而增大了微薄膜与刚性基底间的间隙，分子力的影响程度降低，固有频率降幅ωe-ω2大于ωe-ω3。高阶模态下频率差小于低阶模态，说明低阶模态下电压对固有频率和分子力关系的影响大于高阶模态时。

5）随着微薄膜厚度的增大，固有频率增大，频率差ωe-ωn（n=2，3）减小，表明随着微薄膜厚度的增大，分子力对固有频率的影响减小，频率差ωe-ω2大于ωe-ω3。随着阶数增加，频率差减小，分子力对固有频率和微薄膜厚度关系的影响减小。

6）随着微薄膜长度增大，微薄膜长宽比（r=b/a）减小，固有频率减小，频率差ωe-ωn（n=2，3）增大，表明随着薄膜长度的增大，分子力对固有频率的影响增强，并且差值ωe-ω2大于ωe-ω3。阶数增加时，频率差ωe-ωn（n=2，3）减小，分子力对固有频率和长度关系的影响减小。

4　结论

本文给出了考虑分子力影响的微薄膜压力敏感元件机电耦合系统动力学方程，推导了对边简支对边自由微薄膜振型方程及频率方程，运用该方程，研究了分子力对机电耦合微薄膜系统固有频率及自由振动的影响规律。结果表明：机电耦合微薄膜系统的固有频率和振型均与分子力有关，同时考虑静电场力加分子力时系统的动力学响应与仅考虑静电场力时系统的动力学响应具有较大的差别。随着系统初始间隙的减小、工作电压的增大、微薄膜厚度的减小以及薄膜长度的增大，分子力对微薄膜机电耦合系统的固有频率影响显著。低阶模态下，分子力必须予以考虑。当初始间隙减小到0.1μm时，Casimir力对固有频率的影响比van der Waals力更加明显，此时应该考虑Casimir力的影响。本文工作有助于研究薄膜式微谐振压力传感器谐振子的动力学理论，研究结果对于MEMS压力传感器进一步小型化具有指导意义。

［1］李琦，武文革，李学瑞，等.康铜薄膜压力传感器的有限元分析［J］.制造业自动化，2013，35（15）：99-101.

［2］Dinesh Kumara D，Kumarc N，Kalaiselvam S，et al.Micro-tribomechanical properties of nanocrystalline TiN thin films for small scale device applications［J］.Tribology International，2015，88：25-30.

［3］Wang Yong-gang，Lin Wen-hui，Li Xiao-meng.Bending and vibration of an electrostatically actuated circular microplate in presence of Casimir force［J］.Applied Mathematical Modelling，2010，35（5）：2348-2357.

［4］Garcia-Alonso A，Garcia J，Castano E，et al.Strain sensitivity and temperature influence on sputtered thin films for piezoresistive sensors［J］.Sensors and Actuators A：Physical，1993，37-38：784-789.

［5］樊尚春，乔少杰，张轩.谐振式硅微结构压力传感器非线性振动特性研究［J］.仪器仪表学报，2007，27（12）：1670-1673.

［6］刘勇，叶湘滨.硅岛式微谐振压力传感器灵敏度分析与仿真［J］.计算机仿真，2008，25（7）：317-321.

［7］张建，丁建宁，王权，等.范德华力对硅基微悬臂梁抗粘附稳定性的影响［J］.机械强度，2007，29（6）：923-926.

［8］Xu Lizhong，Zhao Dan.Effects of the molecular forces on the free vibration of electromechanical integrated electrostatic harmonic actuator［J］.Precision Engineering，2013，37（2）：275-285.

［9］赵亚溥.纳米与介观力学［M］.北京：科学出版社，2014：430-443.［10］赵亚溥.表面与界面物理力学［M］.北京：科学出版社，2012： 40-47.

［11］Herbert H W，James R M.机电动力学［M］.华中机电教研室，译.北京：机械工业出版社，1982：33-39.

［12］曹志远.板壳振动理论［M］.北京：中国铁道出版社，1989：13-25.

［13］刘延柱，陈文良，陈立群.振动力学［M］.北京：高等教育出版社，1998：201-206.

Influence of molecular forces on dynamic characteristic of electromechanical coupling thin film pressure sensitive element

SUN Li-bo1，XU Li-zhong2，DING Ling3
（1.School of Environmental and Chemical Engineering，Yanshan University，Qinhuangdao Hebei 066004，China；2.School of Mechanical Engineering，Yanshan University，Qinhuangdao Hebei 066004，China；3.School of Information Science and Technology，Yanshan University，Qinhuangdao Hebei 066004，China）

The dynamical equations of electromechanical coupling thin film are deduced by considering molecular forces.The vibration and frequency equations of thin film with two opposite edges simply supported and other two free are derived.Using the equations，the influences of the molecular forces on natural frequency and free vibration are investigated.Results show：the molecular forces have obvious influences on the natural frequency.As the initial clearance drops，voltage grows，the thickness decreases，and the length increases，the influences becomes larger.As the order number of the modes decreases，the effects on the natural frequency are more significant.At clearance t0=0.1 μm，the Casimir forces have more obvious effects on the natural frequency than van der Waals forces，and the Casimir forces must be considered.The results are helpful to the study of dynamic characteristics of thin film resonant pressure sensor and can be applied to MEMS dynamic design.

two opposite edges simply supported and other two free；electromechanical coupled；thin film；van der Waals force；Casimir force；MEMS

TH113.8

A DOI：10.3969/j.issn.1007-791X.2015.06.009

1007-791X（2015）06-0523-08

2015-08-11 基金项目：国家自然科学基金资助项目（51275441）；河北省科学技术研究与发展计划资助项目（13961701D）；河北省教育厅科学研究计划（Z2012031）

孙丽波（1974-），女，辽宁辽阳人，博士，高级实验师，主要研究方向为微机电系统动力学；*通信作者：许立忠（1962-），男，河北昌黎人，博士，教授，博士生导师，主要研究方向为现代机械传动基础理论与制造技术、机电集成传动、微型机电系统，Email：xlz@ysu. edu.cn。