气膜条件下车厢表面摩擦阻力计算理论研究*

谢小鹏 曹立峰 曾建豪

(华南理工大学 机械与汽车工程学院，广东 广州510640)

本研究所述的气膜条件是指在厢体表面渗出空气并形成一层表面空气膜的状态. 厢式运输车在平直道路上行驶时，其空气阻力主要由压差阻力和摩擦阻力组成. 相关研究表明，当车速超过100 km/h时，发动机功率的65%左右需要用来克服空气阻力［1］.对于厢体较短的厢式运输车，由于车身侧面的气流摩擦阻力要小于车体前后的压差阻力，通过减少侧面摩擦阻力来实现减阻的方法没有引起研究者的足够关注.但随着厢体长度的增加，摩擦阻力在总阻力中所占的比重逐步增大，并成为风阻阻力的重要组成部分.因此，通过减少厢体表面与空气之间的摩擦阻力来实现厢式运输车空气阻力的降低是有意义的.

国内外关于表面减阻的研究成果很多，就减阻方法而言，减阻主要包括仿生学减阻［2-6］、微气泡或气膜减阻［7-10］、聚合物添加剂减阻［11-13］等.其中气膜减阻是一种简单并且容易实现的减阻方法. 传统的气膜减阻方法目前多采用液体介质中空气成膜减阻的方式，比较常见于船舶、潜艇，以及鱼雷等水下航行器的减阻等方面，其技术原理是在运动主体周边空间导入空气，形成气液两相混合流或气流薄膜，使运动主体接触的黏性介质发生改变，由于介质密度、黏度的减小，减少运动主体与水之间的摩擦阻力［14］.而本研究将气膜减阻定义为:在外部高速气流与厢体表面之间形成一层相对车体表面为零速或者低速的渗透动态空气膜，以减少和部分隔断外部高速气流与车厢体表面的直接摩擦作用，从而减少厢体表面的摩擦阻力，实现减阻［10］. 虽然气膜减阻在船舶、舰艇和鱼雷等方面有所尝试，但关于气膜减阻在厢式运输车厢体减阻中的应用，目前国内外还鲜见报道.文献［9］提出了薄膜渗透氢气法降低列车空气阻力的构想，但由于氢气是一种易燃易爆的气体，导致在列车表面析出氢气减阻的方法存在严重的安全隐患，目前还没有实际应用. 文献［10］通过实验证实了气膜减阻应用在厢式运输车厢体表面减阻上是有效的，然而在气膜减阻机理和气膜条件下厢体表面摩擦阻力计算模型的建立等方面缺少探讨.针对此问题，本研究从理论上探讨了气膜实现厢体表面减阻的原因，提出了边界层加厚理论、混合降速理论、边界层加厚-混合降速理论3 种减阻理论假说，并建立这3 种理论假说条件下的厢式运输车厢体表面气流摩擦阻力计算模型.

1 气膜减阻机理

厢式运输车的气膜减阻示意图如图1 所示. 气泵将空气泵入到空气腔中，在内部压强的作用下，空气腔中的空气从渗透小孔中溢出，在厢体表面上形成一层渗透空气流，即形成厢体表面有气膜条件.当厢体表面没有气膜时，外部高速空气流与厢体表面之间存在直接的摩擦作用;当厢体表面有气膜时，渗透空气流在一定程度上能起着隔离高速气流、减少空气摩擦阻力的效果.

图1 厢式运输车的气膜减阻示意图Fig.1 Schematic diagram of air film drag reduction on a van

为了近似计算厢体表面的摩擦阻力，本研究假定厢体表面是类似于表面光滑的平板结构，并按照平板边界层的摩擦阻力计算方法进行厢体表面摩擦阻力的近似计算.

1.1 边界层加厚理论

摩擦阻力是由于空气的黏性在车身表面产生的切向力造成的，厢体越长，摩擦阻力的作用就愈加明显.当厢体表面近似为光滑平板时，可将厢体表面近似为平板边界层进行分析. 平板边界层分为层流边界层、过渡区和湍流边界层3个部分，在边界层的底部还存在一个层流底层，如图2 所示.图2(a)为无气膜时的平板边界层分布，图2(b)为有气膜时的平板边界层分布.

边界层是指高雷诺数绕流中紧贴物面的黏性力不可忽略的流动薄层［15］.文中的边界层厚度是指高速气流的边界层外边界与厢体表面之间的垂直距离.由于本研究假设厢体表面的气流为定常流动(即流体流动时，流体中任何一点的压力、速度和密度都不随时间变化)，当厢体表面有气膜渗出时，相当于将原来的边界层整体向外排挤，起到了加厚原边界层的作用，空气膜和原有的边界层厚度一起叠加形成了新的边界层厚度.对比两者可以发现，通气后由于渗透空气流的加入，使得平板的层流底层厚度增加，整体的边界层厚度也随之增大.

图2 平板边界层Fig.2 Flat-plate boundary layer

流过厢式运输车厢体表面的气流属于外流，通常将这些外流分为壁面附近的黏性影响区和外部的无黏性区.黏性影响区仅局限在厢体表面附近的边界层内部，边界层外部可以忽略黏性效应的影响，可按无黏性流体来处理［15］.所以分析厢体表面的受力情况，重点在于分析边界层内部气流对厢体表面的黏性阻力作用.

无论流体处于层流还是湍流状态，边界处所受到的剪切力均取决于边界处的速度梯度和边界层流体的动力黏度［9］.根据牛顿内摩擦定律，切应力:

式中， 为切应力，μ 为空气的动力黏度，du/dy 为垂直于流体接触面上的速度梯度.

厢体表面在无气膜和有气膜时，层流边界层内部气流的速度分布如图3 所示.

图3 中，u1(x，y)和u2(x，y)分别为无气膜和有气膜时，边界层内部流体的速度分布，U 为外部流体的速度.边界层2 相对于边界层1 而言，即通入空气后，在厢体表面上形成一层内部渗透气膜层，使层流底层厚度增加，边界层厚度增大.由于黏附在厢体表面附近的内部渗透空气流为低速流体，对边界层2 内部气流的速度有所抑制，使得速度梯度减小，由式(1)可知，厢体表面受到的剪切力降低.

图3 厢体表面层流边界层Fig.3 Laminar boundary layer on the van body surface

根据气体动力学的计算，当气体在没有热交换的条件下做低速(速度小于100 m/s)流动时，密度变化的影响可以忽略不计［15］.文中高速空气流和渗透空气流的速度均远小于100 m/s，故可认为空气的密度不变.此外，由于外部气流是相对厢体渗透空气膜表面平行流动，其对气膜产生的表面垂直压力可忽略不计.因此理论推导中外部气流与渗透空气膜两者均可按照定常流动进行处理. 同时假设空气流体与厢体表面之间无能量传递，空气流体的温度保持不变.

以二维恒定层流边界层流动为例进行分析.对于二维恒定层流边界层微分方程，结合其边界条件:

1)当y = 0 时，ux= uy= 0 ，

2)当y = ∞时，ux= U = U∞=const;得到简化后的层流边界层微分方程组:

经过相关求解计算，得到层流边界层厚度:

式中:δ 为厢体表面无气膜时的边界层厚度;ν 为流体的运动黏度;n 为常数系数，在不同流速分布条件下，式(3)中n 的值不同［16］.

无气膜时厢体表面上的切应力表达式为

当厢体表面有气膜时，边界层厚度增加，为了研究有气膜时的边界层厚度与厢体表面摩擦阻力之间的关系，引入一个常数系数k(k ＞1)，并假设厢体表面有气膜时的边界层厚度δ′为无气膜时的k倍，即

可推知有气膜时厢体表面的切应力为

对于厢体表面的二维恒定层流边界层，对比式(4)和(6)可知，有气膜时厢体表面受到的切应力是无气膜时的1/k 倍.

1.2 混合降速理论

因为气流对厢体表面的摩擦阻力集中在边界层内部，所以分析气流对厢体表面的摩擦阻力时，可以将其转化为对厢体表面边界层内部气流的分析. 假设未通气时，边界层1 内部气流的整体质量为m，等效的气流平均速度为;通入空气后，边界层2内部混合后的气流整体质量为m +Δm，其中Δm 为通入空气后，边界层2 内部气流整体质量的增加量，等效的气流平均速度为. 无气膜、有气膜时厢体表面边界层内部气流的等效厚度分别如图4(a)所示的蓝色区域和图4(b)所示的红色区域.

图4 厢体表面边界层的等效厚度Fig.4 Equivalent thickness of the boundary layer on the van body surface

根据动量守恒定律，在厢体表面无气膜和有气膜两种情况下，边界层内部气流的动量均与外部的高速气流产生的动量相平衡，所以可得

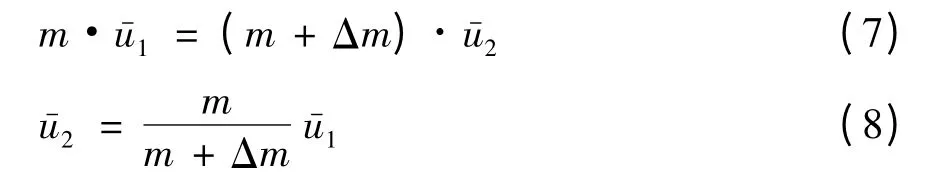
1.3 边界层加厚-混合降速理论

边界层加厚-混合降速理论综合了前两者的思想，假设通入空气后，厢体表面的边界层厚度增加，以及渗透空气流与原始边界层内部气流的混合是同时发生的，使该理论更加符合实际，故以其为主导.由壁面切应力公式［16］可知，壁面边界层厚度δ 越大，流体与壁面之间的切应力 0 就越小.同理，在厢体表面有渗透空气流时，这部分新加入的渗透空气流将原始的边界层向外排挤，从而使新形成的边界层厚度增加，导致厢体表面的摩擦阻力减小.

两气流混合层流动如图5 所示，两股速度不同的平行流，设外部高速气流的速度为u′1，厢体表面渗透空气流的速度为u′2，并且u′1＞u′2.当这两股平行流在交界面汇合时，由于交界面处的速度不连续，存在强烈的剪切作用，同时在空气粘性的作用下，交界面上方的高速气流的速度逐渐减小，交界面下方的渗透空气流的速度逐渐增大，最终在交界面处的速度达到稳定状态，实现了混合后气流整体速度的降低.

图5 混合层流动Fig.5 Mixing layer flow

2 摩擦阻力计算模型的建立

分别从上述边界层加厚理论、混合降速理论、边界层加厚-混合降速理论的角度，探讨厢体表面摩擦阻力计算模型的建立问题.

首先判断厢体表面气流的流态，然后根据流态进行厢体表面摩擦阻力的计算. 已知空气密度ρ =1.225 kg/m3，运动黏度ν =1.5 ×10-5m2/s.由于不同型号厢式运输车的厢体尺寸大小不一，本研究以一般常见的厢式运输车为例，假设厢体的长度l 为12 m，高h 和宽b 均为2.2m，行驶速度U0= 25m/s，则厢体表面气流的雷诺数为:由厢体表面气流的雷诺数可知厢体表面气流的流态为湍流. 故在上述3 种理论假说条件下，均采用平板湍流边界层的阻力计算方法［16］进行厢体表面摩擦阻力的计算.

2.1 边界层加厚理论模型计算

为了探讨有气膜时厢体表面的摩擦阻力计算问题，首先从无气膜时的受力进行分析，然后推导出有气膜时厢体表面所受到的摩擦阻力，推导计算过程如式(9)-(14)所示.

无气膜时厢体表面湍流边界层的流速分布取决于厢体表面气流的雷诺数，而文中Rel= 2 ×107，故选用流速分布的1/7 指数公式进行计算:

厢体表面湍流边界层的壁面切应力可以参照圆管恒定均匀湍流的结果得出［16］:

经过推导可以得到边界层厚度:

式中，Rex为图3 所示坐标系中厢体表面在坐标点x处的雷诺数，即Rex=Ux/ν.

无气膜时厢体表面一侧的摩擦阻力:

相对于无气膜而言，有气膜时增加了厢体表面的边界层厚度，进而引起切应力和摩擦阻力的变化.根据前面的假设:通入空气后，边界层厚度δ′= kδ(k ＞1 )，故可推知有气膜时的厢体表面切应力:

有气膜时厢体表面一侧的摩擦阻力:

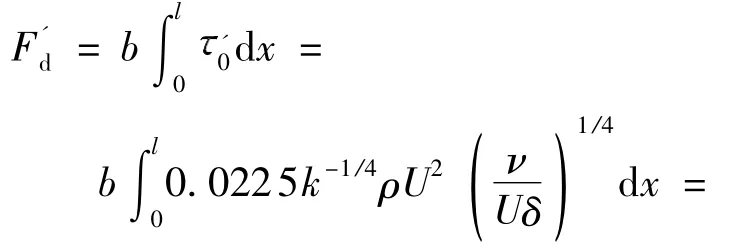
通过对比式(12)和(14)可知，厢体表面在有气膜时所受到的摩擦阻力为无气膜时的k-1/4倍.常数系数k(k ＞1)值越大，表明当边界层厚度随厢体表面的气膜厚度增大而增大时，厢体表面受到的摩擦阻力随着气膜厚度的增大而减小.

2.2 混合理论模型计算

在有气膜条件下，厢体表面渗透出的低速空气流与外部的高速气流混合后，导致来流速度降低.由式(8)可知，混合后的气流速度

有气膜时厢体表面的切应力:

有气膜时的厢体表面一侧摩擦力:

从能量消耗的角度分析，在未通气时，边界层内部气体的能量:

通气时，混合后边界层内部气体的能量:

由式(17)、(18)对比发现，由于Δm ＞0 ，可知E2＜E1，即通入空气后，边界层内部混合气体的能量要小于未通气时边界层内部混合气体的能量，从而实现减阻节能效果.

2.3 边界层加厚-混合降速理论模型计算

根据边界层加厚理论和混合降速理论的综合，得到边界层加厚-混合降速理论的摩擦阻力计算模型.

有气膜时厢体表面的切应力:

有气膜时的厢体表面一侧摩擦力:

由式(20)可知:有气膜时，一方面，混合后的空气流速度降低;另一方面，边界层的厚度增加. 在两方面的共同影响下，实现了气膜条件下厢体表面摩擦阻力的降低，并且厢体表面在有气膜时所受到的摩擦阻力为无气膜时的倍.

综合上述3 种理论计算模型，即由式(14)、(16)、(20)可知，当待定参数k 以及Δm 与m 的相对大小关系已知时，结合其他的已知参数，即可求出气膜条件下厢体表面在各自理论假说下所受到的摩擦阻力.

3 结语

针对厢式运输车厢体表面气膜减阻问题，在假定厢体表面为类似于光滑平板的基础上，分别从边界层加厚理论、混合降速理论、边界层加厚-混合降速理论的角度，探讨了气膜减阻的减阻机理，建立了气膜条件下厢体表面的摩擦阻力计算模型. 在上述3 种理论假说条件下，通过定性对比分析厢体表面在有气膜和无气膜时各自所受到的摩擦阻力，均得出厢体表面在有气膜时的摩擦阻力较小，这与笔者的前期实验研究结果［10］趋于一致，为气膜减阻在厢体表面减阻中的实际应用提供了理论基础.

［1］McCallen R C，Salari K，Ortega J M，et al.DOE’s effort to reduce truck aerodynamic drag-joint experiments and computations lead to smart design［R］. Livermore:Lawrence Livermore National Laboratory，2004.

［2］Chen Hua-wei，Rao Fu-gang，Shang Xiao-peng，et al.Biomimetic drag reduction study on herringbone riblets of bird feather［J］.Journal of Bionic Engineering，2013，10(3):341-349.

［3］Bixler G D，Bhushan B.Fluid drag reduction and efficient self-cleaning with rice leaf and butterfly wing bioinspired surfaces［J］.Nanoscale，2013，5(17):7685-7710.

［4］Dean B，Bhushan B.Shark-skin surfaces for fluid-drag reduction in turbulent flow:a review ［J］. Philosophical Transactions of the Royal Society A:Mathematical，Physical and Engineering Sciences，2010，368(1929):4775-4806.

［5］Han Xin，Zhang De-yuan，Li Xiang，et al. Bio-replicated forming of the biomimetic drag-reducing surfaces in large area based on shark skin［J］.Chinese Science Bulletin，2008，53(10):1587-1592.

［6］张祯华.以聚氨酯为基质的柔性仿生减阻材料的制备及其减阻性能研究［D］.广州:华南理工大学材料科学与工程学院，2012.

［7］Sayyaadi H，Nematollahi M.Determination of optimum injection flow rate to achieve maximum micro bubble drag reduction in ships;an experimental approach［J］. Scientia Iranica，2013，20(3):535-541.

［8］Jamaluddin A. Micro-bubble drag reduction on a high speed vessel model ［J］. Journal of Marine Science and Application，2012，11(3):301-304.

［9］叶立国. 薄膜渗透氢气法降低列车空气阻力的构想［J］.铁道机车车辆，2002(6):36-37.Ye Li-guo.Conceive plan about decreasing train air resistance by thin-film-penetration-hydrogen［J］. Railway Locomotive ＆ Car，2002(6):36-37.

［10］谢小鹏，曹立峰，曾建豪.厢式运输车厢体的气膜减阻法试验研究［J］.润滑与密封，2014，39(4):89-92.Xie Xiao-peng，Cao Li-feng，Zeng Jian-hao.Experimental research on air film drag reduction of van body［J］.Lubrication Engineering，2014，39(4):89-92.

［11］Al-Yaari M，Al-Sarkhi A，Abu-Sharkh B. Effect of drag reducing polymers on water holdup in an oil-water horizontal flow ［J］. International Journal of Multiphase Flow，2012，44:29-33.

［12］Omrani P S，Delfos R，Boersma B J. Polymer induced drag reduction in a turbulent pipe flow subjected to a coriolis force ［J］. Flow，Turbulence and Combustion，2012，89(4):589-599.

［13］White C M，Mungal M G. Mechanics and prediction of turbulent drag reduction with polymer additives［J］.Annual Review of Fluid Mechanics，2008，40:235-256.

［14］陈克强，黄丽.高速艇尾部横剖面面积曲线变化对气泡减阻效果影响的数值模拟［J］.船海工程，2009，38(6):32-36.Chen Ke-qiang，Huang Li. Numerical simulation of the micro-bubbles resistance reduction effect of different curves of transverse sectional area ［J］. Ship ＆ Ocean Engineering，2009，38(6):32-36.

［15］丁祖荣. 流体力学(上)［M］. 北京:高等教育出版社，2003.

［16］陈玉璞，王惠民.流体动力学［M］.北京:清华大学出版社，2013.