脉冲型地震作用下斜拉桥纵向响应的简化计算*

徐艳　黄永福　李建中

(同济大学 土木工程防灾国家重点实验室, 上海 200092)

脉冲型地震作用下斜拉桥纵向响应的简化计算*

徐艳黄永福李建中

(同济大学 土木工程防灾国家重点实验室, 上海 200092)

摘要：为研究近断层脉冲作用对斜拉桥地震响应的影响，在研究近断层地震动特性的基础上，利用最小二乘法进行脉冲模型数值拟合，通过等效模态法将复杂斜拉桥在纵桥向简化为单质点体系，建立、求解近断层脉冲作用下斜拉桥纵桥向的运动微分方程，得到斜拉桥塔顶位移、塔底弯矩与速度脉冲周期及幅值的解析关系，由此得出结构地震响应随脉冲参数变化的规律，并分别通过独塔和双塔斜拉桥的有限元分析对该方法的正确性进行验证，结果表明该方法简单可行，误差在工程可接受范围内.

关键词：斜拉桥；地震响应；近断层地震；脉冲模型；等效模态法；最小二乘法

美国LomaPrieta地震和Northridge地震、土耳其Izmit地震、日本Kobe地震以及我国台湾集集地震等震后灾害表明，断层附近建筑物的毁坏程度比远离断层区域严重得多[1-4]，分析研究发现，这些地震记录都存在由断层引发的强烈地震脉冲作用，具有显著的集中性、地表破裂、永久位移和断裂的方向性效应、速度大脉冲、上盘效应等特点，其中速度大脉冲是引起近断层桥梁结构倒塌或严重破坏的主要原因.在过去40多年的研究中，学者们在近断层脉冲对结构的影响方面做了大量工作，随着对地震动新特性的不断认识和发现，近年来国内外有学者鉴于近断层地震记录数量的限制，致力于研究近断层脉冲的简化数值模拟.

Alavi、Sasani等[5-6]认为，结构在简化脉冲与近断层实际记录下的响应具有较大的相似性，并建议通过脉冲周期、幅值和半周期个数等参数来模拟近断层记录中的脉冲响应；Somerville[7]将近断层地震视为简单冲击波，统计得到脉冲参数与震级、震中距的关系；Alavi等[5]在Somerville的简化脉冲模型基础上，提出了P2型三角形速度脉冲模型；Makris等[8]认为近断层地震波由不同周期的正弦或余弦波组合而成，用三角函数模拟近断层地震波的主要脉冲；Menun等[9]提出一种正弦函数与指数函数相结合的新模型，采用非线性回归方法确定其模型中的参数.李新乐等[10]引入幅值对脉冲强度的贡献率以及半周期循环个数，可以模拟任意长度的持时和所需数目的卓越峰(谷)值点的速度脉冲波形，并可同时控制峰点(或谷点)的幅值.

上述模型中，Makris等[8]提出的三角函数脉冲以及Alavi等[5]提出的P2型三角形速度脉冲模型应用较为广泛，而其他含有复杂参数的简化模型由于其表达式的复杂性和各自的局限性，在实际结构地震反应分析中并没有得到广泛的应用，尤其在大跨度复杂桥梁抗震计算分析中，依然采用输入带有脉冲的地震动时程进行时间积分求解，与一般地震动求解并无差别，在一定程度上影响了桥梁工程技术人员从总体上理解和把握这一地震动新特性对桥梁结构产生的影响；另一方面，斜拉桥大都采用漂浮体系或半漂浮体系，其自振周期长，隔震性能良好，随着我国交通网络的规划和发展，在断层附近甚至跨越断层修建都不可避免，如何快速简便地把握脉冲特性与桥梁结构地震响应之间的规律，不但可以节约大量计算成本，也可为桥梁工程技术人员在抗震初步设计阶段提供更多的选择.

漂浮体系斜拉桥第一阶振型通常为主梁纵飘，它对斜拉桥主塔底部响应的贡献一般都达到总反应的90%左右，因此理论上斜拉桥纵向可以简化为一个单质点体系，这使得斜拉桥在简化脉冲输入下的地震响应解析解的得到成为可能，也便于研究地震荷载与斜拉桥地震响应之间的普遍规律.

基于以上研究，文中将斜拉桥纵桥向简化为单质点体系，把近断层地震波模拟为简单函数速度脉冲，建立并求解运动微分方程，推导出结构响应与速度脉冲周期Tp、幅值V的解析关系，并通过参数分析，得到近断层地震作用下斜拉桥塔底响应与简化速度脉冲输入的规律，提出一套简便可行的简化计算方法，最后通过一座独塔斜拉桥和一座双塔斜拉桥的有限元计算结果对提出的计算方法进行验证.

1单质点体系简化的等效模态法

针对斜拉桥单质点的简化方法，已有国内外学者做过很多尝试[11-13]，其基本原理都是基于Chopra[14]在结构动力学中提出的有效振型质量和有效振型高度方法，即等效模态法.

斜拉桥的大部分质量集中在主梁和桥面系上，因此在地震荷载作用下的惯性力也主要集中于主梁和桥面系.其惯性力通过斜拉索和塔梁间纵向连接装置传递至主塔，从水平地震力的传力路径来看，主梁的惯性力主要通过斜拉索传到主塔.理论研究证明，当把主梁全部质量(对于双塔斜拉桥，为主梁的一半质量)堆聚在锚固区顶端(即最外侧拉索在主塔上的锚固位置)时，简化模型与原桥相应结果的误差均在可接受范围内[15].因此，斜拉桥模型可从全桥模型简化为具有塔顶集中质量和塔身分布质量的单塔模型；将单塔模型的质量全部集中于某高度的一个质点上，于是单塔模型便简化成了单质点模型，如图1所示.图1中m*由主梁质量和主塔质量组成，称为有效振型质量，H*称为有效振型高度.

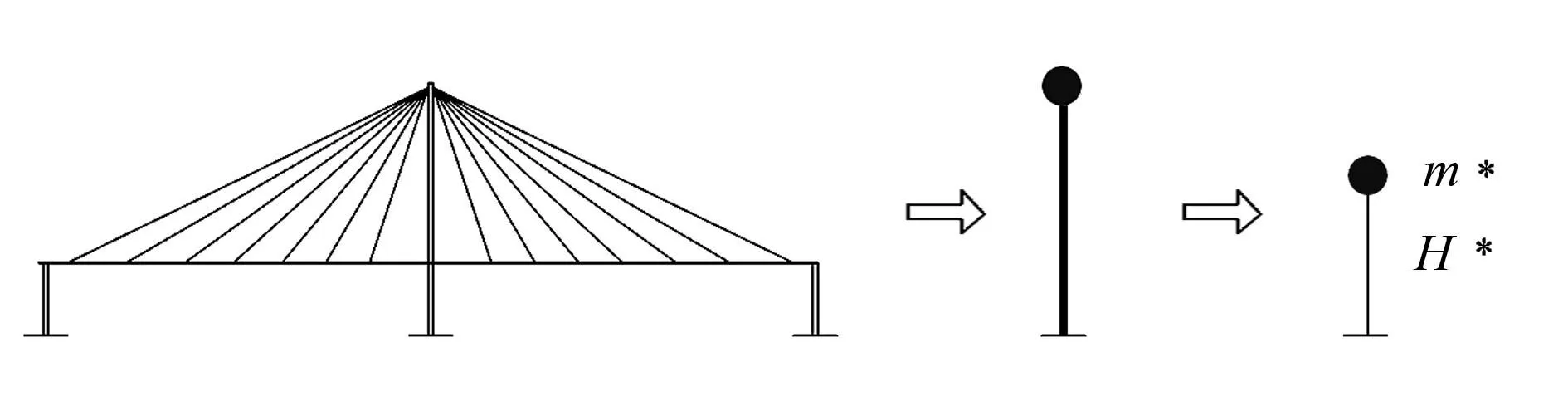
全桥模型　 单塔模型 单质点模型图1　斜拉桥简化过程Fig.1　Simplification process of cable-stayed bridge

2近断层地震波的简化脉冲模型

通过对地震动记录的统计可发现，速度脉冲通常分为两类：由前导方向性效应引起的双向速度脉冲和由滑冲效应引起的单向速度脉冲.后者为半周期速度脉冲，它会产生较大的位移脉冲，这种错动位移仅对跨断层结构产生作用，因此单向速度脉冲在近断层结构中不做考虑，而双向速度脉冲通常反应在加速度记录中也有相应的加速度脉冲，会对结构产生数倍于普通地震动的地震响应.图2为Makris等[8]提出的Type-B正弦速度脉冲模型和Alavi等[5]提出的P2矩形加速度脉冲模型.

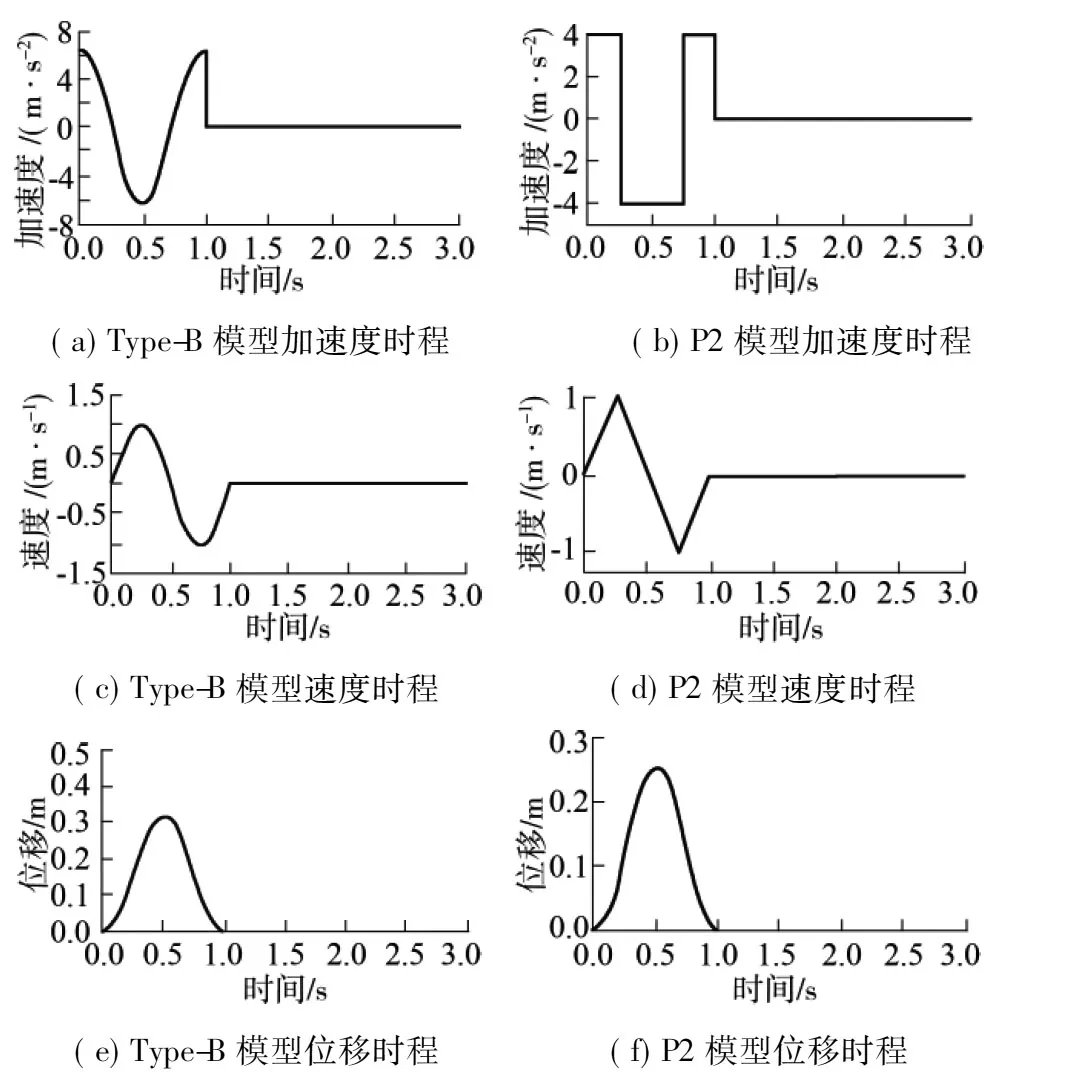
图2　Type-B模型和P2模型的加速度、速度、位移时程图Fig.2　Acceleration,velocity,displacement time histories of Type-B and P2 models

从美国太平洋地震工程研究中心PEER的数据库网站上(http:∥peer.berkeley.edu/)选取11条近断层地震动记录，它们具有典型的前导方向性效应，断层距R<15km，矩震级M>6.0，水平向速度峰值PGV>40cm/s，脉冲周期分布于2~5s之间，是具有代表性的近断层地震记录.根据Type-B模型和P2模型的函数表达，利用最小二乘法对11条地震波进行拟合，得到简化脉冲模型的参数如表1所示.

表1近断层速度脉冲的拟合参数Table1Fittedparametersofnear-faultvelositypulse

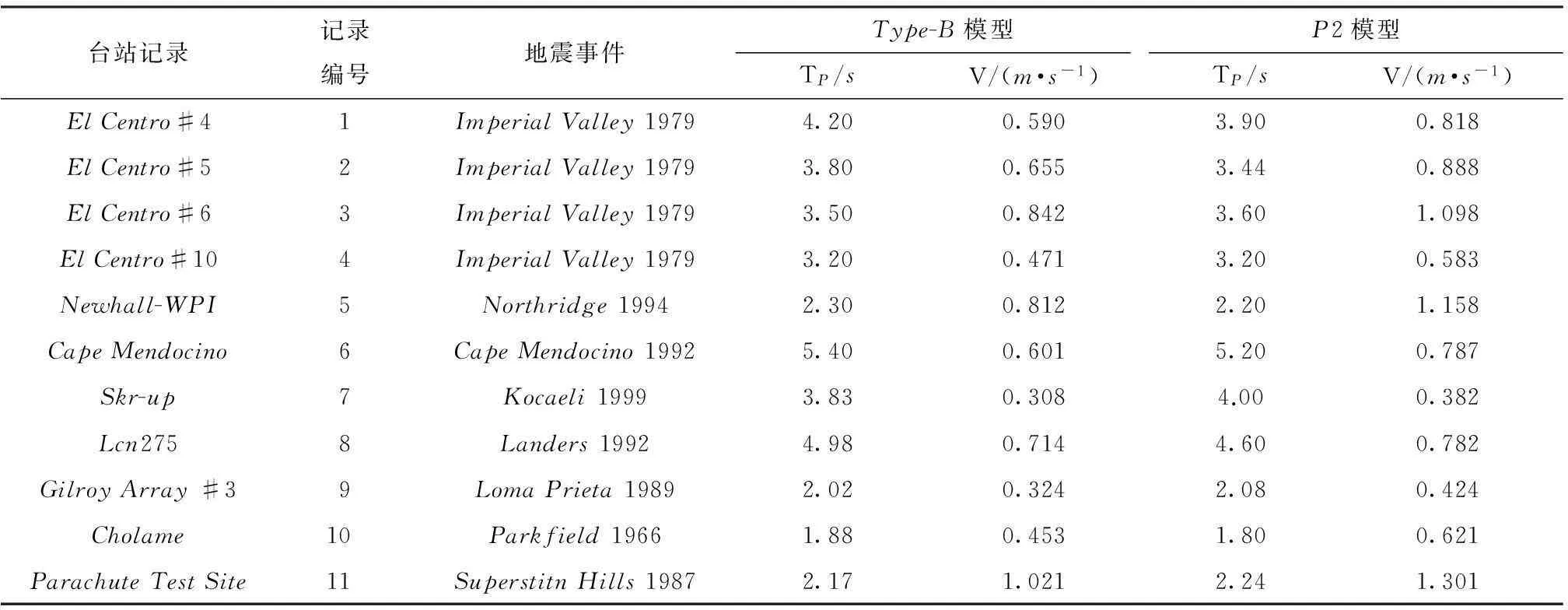
台站记录记录编号地震事件Type-B模型P2模型TP/sV/(m·s-1)TP/sV/(m·s-1)ElCentro#41ImperialValley19794.200.5903.900.818ElCentro#52ImperialValley19793.800.6553.440.888ElCentro#63ImperialValley19793.500.8423.601.098ElCentro#104ImperialValley19793.200.4713.200.583Newhall-WPI5Northridge19942.300.8122.201.158CapeMendocino6CapeMendocino19925.400.6015.200.787Skr-up7Kocaeli19993.830.3084.000.382Lcn2758Landers19924.980.7144.600.782GilroyArray#39LomaPrieta19892.020.3242.080.424Cholame10Parkfield19661.880.4531.800.621ParachuteTestSite11SuperstitnHills19872.171.0212.241.301

这11组脉冲模型在形状、傅里叶谱、反应谱上与实际地震波均十分相似.图3所示为地震记录ElCentro#6的P2模型、Type-B模型的波形拟合结果；该地震记录的实际地震波、P2模型、Type-B模型的傅里叶谱及反应谱如图4所示.从傅里叶谱来看，两种模型在能量集中的波谱频率段上都与ElCentro#6非常吻合；值得一提的是，简化的脉冲模型在反应谱形状上相差较大，尤其是高频段，但在长周期成分上(T>2s)3条线基本吻合.因此，对于斜拉桥等长周期结构，低频成分的影响起主要作用，这也是斜拉桥得以用脉冲简化模型研究近断层地震作用的原因之一.

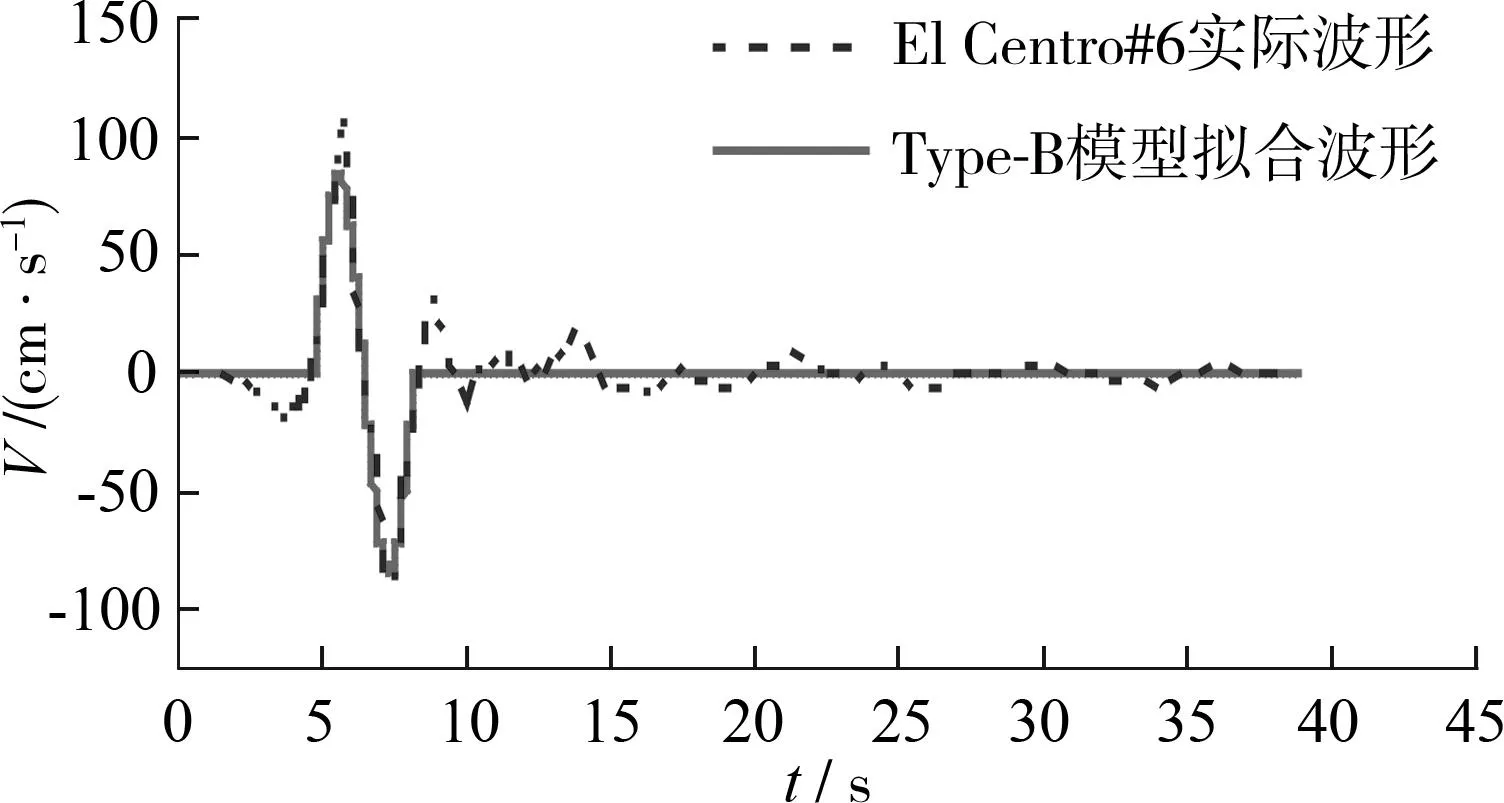
(a)Type-B模型拟合

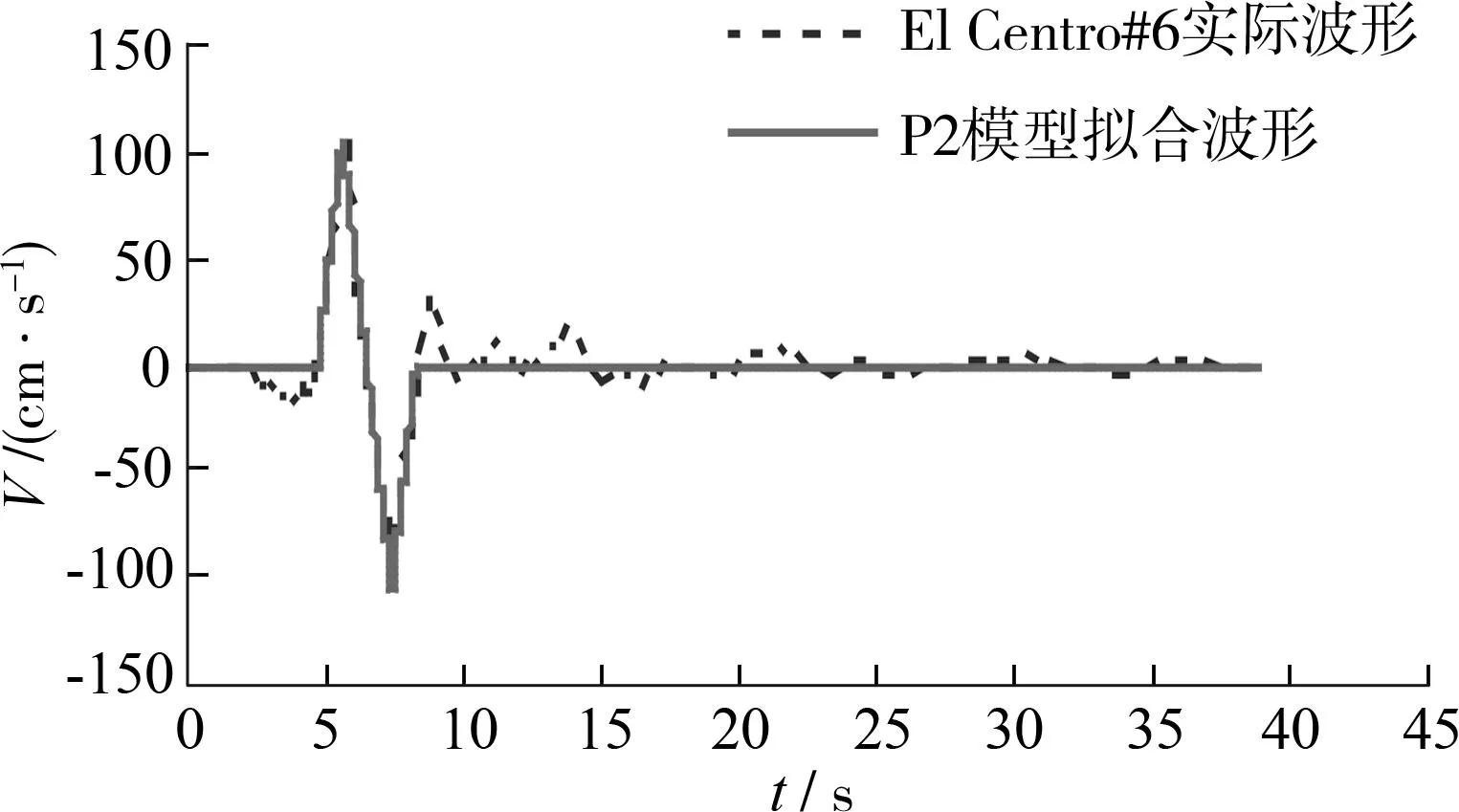
(b)P2模型拟合图3　地震记录El Centro#6的Type-B模型和P2模型的拟合波形Fig.3　Fitted shapes of Type-B and P2 models of earthquake record El Centro#6

(b)反应谱图4　地震记录El Centro#6与其Type-B模型、P2模型的傅里叶谱与反应谱Fig.4　Fourier spectra and response spectra of earthquake record El Centro#6 as well as its Type-B and P2 models

3斜拉桥地震响应简化计算方法

将简化脉冲作为纵桥向地震输入，建立单质点体系运动微分方程如式(3)和(4)：

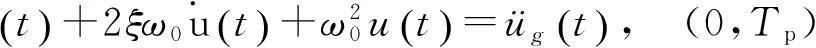
(3)

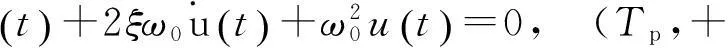
(4)

其中：ξ为结构阻尼比，ω0为结构无阻尼自振频率.

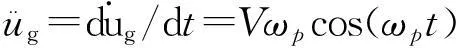
u(t)=

(5)

其中：

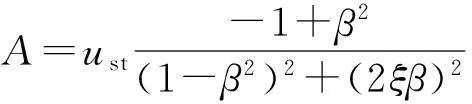
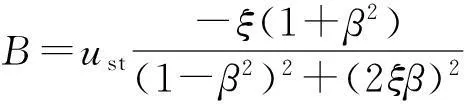
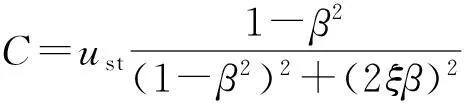
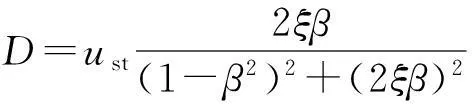
ust=Vβ/ω0，为结构的静力位移；β=ωp/ω0，为荷载频率与结构固有频率之比.

对于P2模型，üg=±V，求解式(3)微分方程得到质点位移表达式：

u(t)=

(6)

其中：

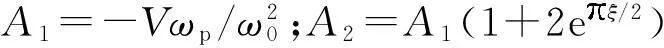
于是，斜拉桥纵桥向塔底弯矩表达式如下：

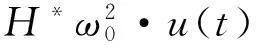
(7)

值得一提的是，对于具有常见平面塔形的斜拉桥，在纵桥向地震作用下，由于塔底地震轴力几乎为零，与单质点模型相应轴力一致，因此不作为研究对象，抗震验算时塔底轴力组合值可取其恒载轴力；对于塔底剪力，文中方法仅考虑了主桥一阶振型，忽略了桥塔的高阶振型影响，实际上剪力往往不是由一阶振型控制的，它受塔高、跨度、质量分布等复杂因素影响，很难用一个简单公式来表达其规律性.但这不妨碍本研究的研究目的，因为桥塔截面的抗弯能力验算并不需要已知剪力，故文中仅给出其塔底弯矩的简化计算表达式.

4验证实例

为了验证上述方法的合理性，文中应用某双塔斜拉桥和某独塔斜拉桥两个实例进行验证.双塔斜拉桥主桥为双塔混凝土箱梁斜拉桥，桥跨布置为50m+110m+380m+110m+50m=700m，桥塔为A型混凝土索塔，索塔总高140m，塔上设置15对斜拉索.主梁采用钢混叠合箱梁，过渡墩及辅助墩为V型墩.独塔斜拉桥主桥采用2×230m=460m独塔斜拉桥方案，主塔采用A型混凝土索塔，塔高150m；塔上共设置17对斜拉索，主梁为钢箱梁，宽37.3m.为简便起见，两座桥的塔底、墩底均与地基固结，纵桥向为半漂浮体系.图5所示为双塔斜拉桥和独塔斜拉桥的有限元模型图.

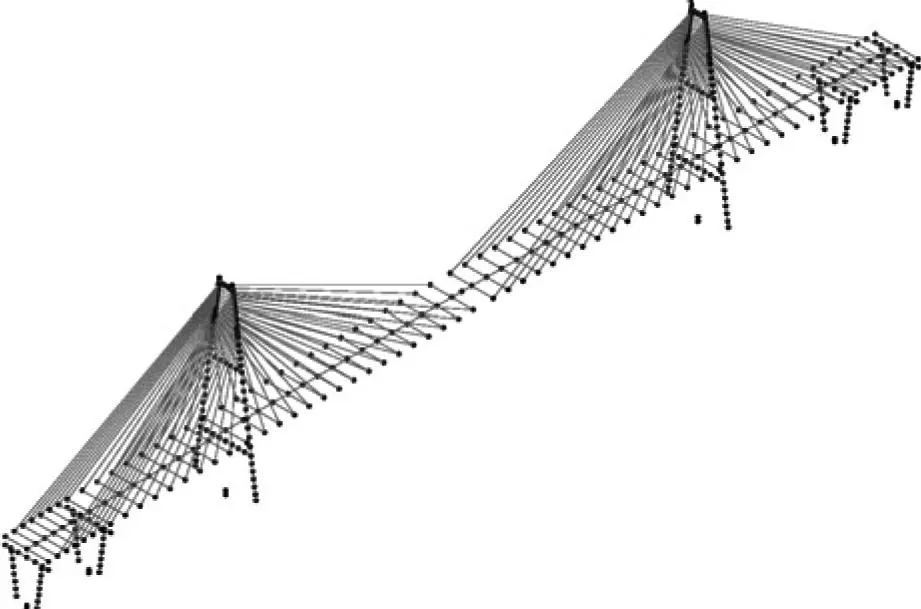
(a)双塔斜拉桥模型 (b)独塔斜拉桥模型

图5双塔斜拉桥和独塔斜拉桥有限元模型

Fig.5Finiteelementmodelsofdouble-towercable-stayedbridgeandsingle-towercable-stayedbridge

为了论证文中方法的适用性，首先根据前文所述应用等效模态法对上述两座斜拉桥进行单质点模型的等效，得到各自的有效振型质量和有效振型高度，如表2所示.

表2单质点模型参数
Table2Parametersofthemodelwithsingledegreeoffreedom

桥型第一阶周期/s单质点周期/s有效振型质量/t有效振型高度/m双塔斜拉桥9.628.7627432130.2独塔斜拉桥6.045.0021069136.0

然后将全桥模型和单质点模型在相同地震输入下的塔底纵向弯矩和塔顶位移进行对比，以全桥模型的有限元计算结果为基准，得到在近断层地震波、Type-B脉冲和P2脉冲输入下，双塔和独塔斜拉桥的塔底纵向弯矩、塔顶位移的无量纲比值,如图6和7所示.

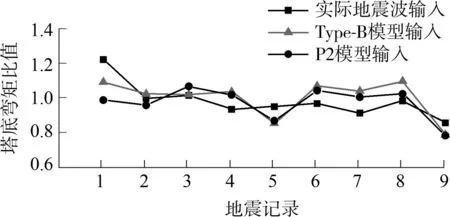
(a)弯矩比值图

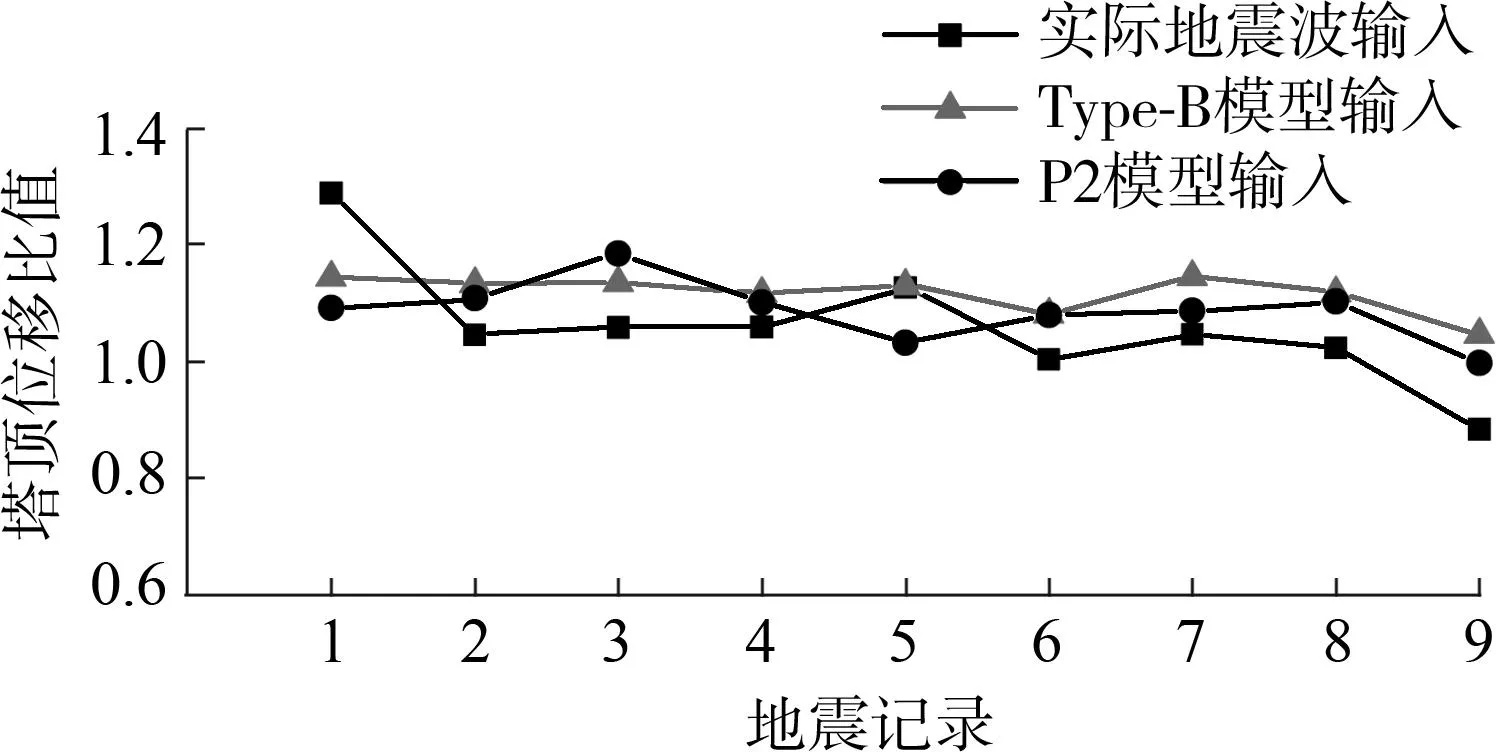
(b)位移比值图图6　双塔斜拉桥模型塔底弯矩比值图与塔顶位移比值图Fig.6　Tower bottom moment ratio and tower top displacement ratio of double-tower cable-stayed bridge

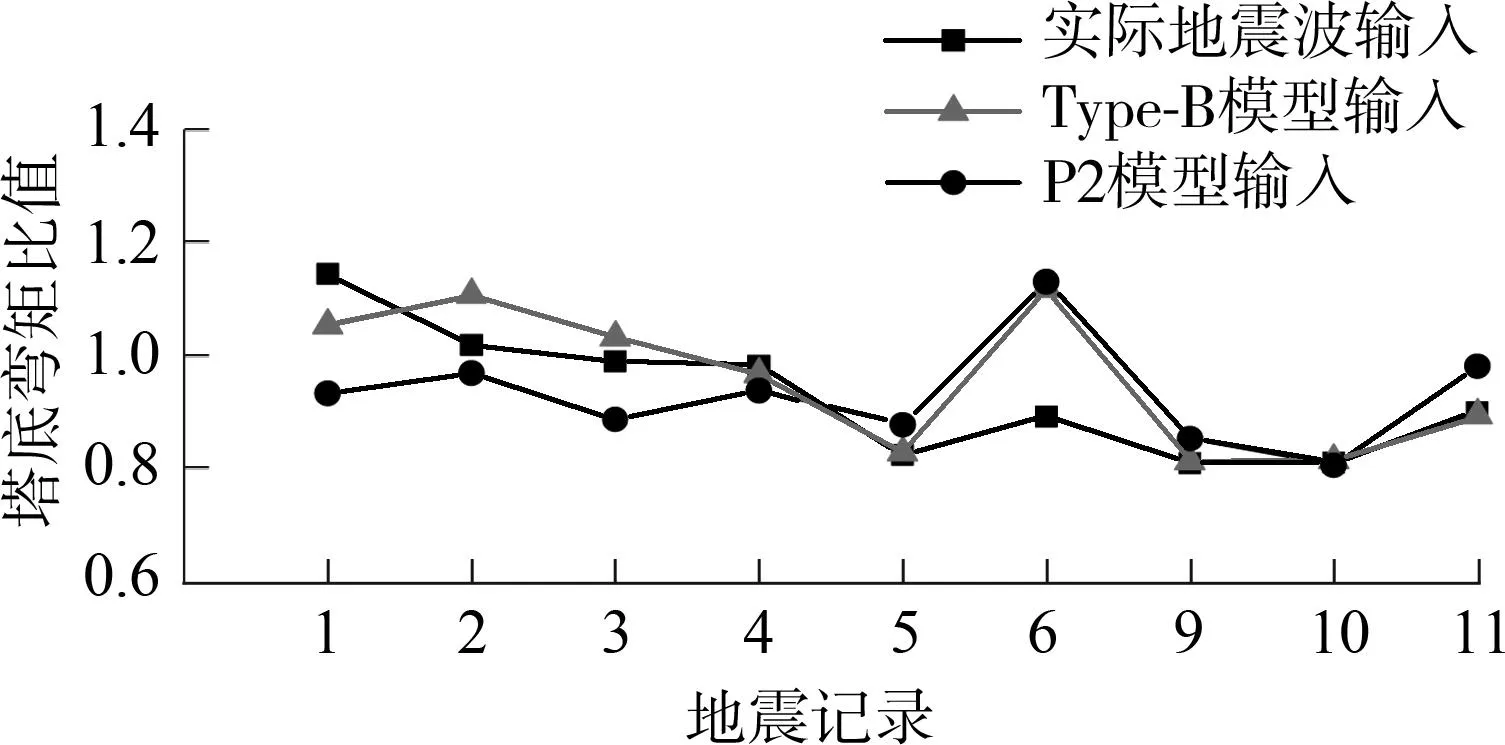
(a)弯矩比值图

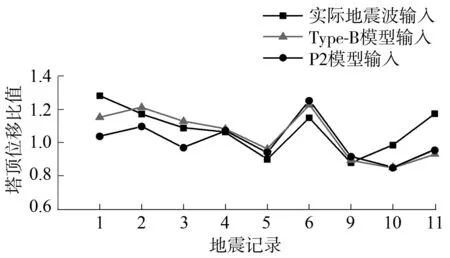
(b)位移比值图图7　独塔斜拉桥模型塔底弯矩比值图与塔顶位移比值图Fig.7　Tower bottom moment ratio and tower top displacement ratio of single-tower cable-stayed bridge

从图6、图7可以看出，无论采用何种地震输入，单质点模型和斜拉桥全桥模型的相应结果比值基本上落在(0.8,1.2)的区间内，虽然存在一定的误差，但相比全桥有限元时程计算，文中方法大大缩短了计算时间，对于工程初步抗震计算而言，误差在可接受的范围内，且对双塔斜拉桥和独塔斜拉桥均适用.

5脉冲参数分析

文中在论证上述计算方法正确可行的基础上，进一步研究速度脉冲模型的周期Tp、幅值V与斜拉桥塔底响应的规律，以及阻尼比对其响应的影响.对斜拉桥单质点体系，输入Type-B脉冲，考虑结构的瞬态反应和稳态反应，分析周期Tp∈(0，50)s、速度脉冲幅值V∈(0，200)cm/s范围内，在不同结构阻尼比下结构内力的变化趋势；得到塔底弯矩最大值与脉冲周期的关系(见图8)，塔底弯矩放大系数(脉冲作用下的塔底弯矩与静力弯矩之比M/Mst)与脉冲频率比ωp/ωo的关系(见图9).

图8表明：塔底弯矩在脉冲周期为11~12s(双塔斜拉桥)和6~7s(独塔斜拉桥)时达到最大值；随着脉冲周期的增大，塔底弯矩迅速减小；当周期大于25s(双塔斜拉桥)和15s(独塔斜拉桥)时塔底弯矩变化趋于平缓，并接近结构在静力荷载作用下的弯矩值；随着阻尼比减小，塔底弯矩增大.

(a)双塔斜拉桥

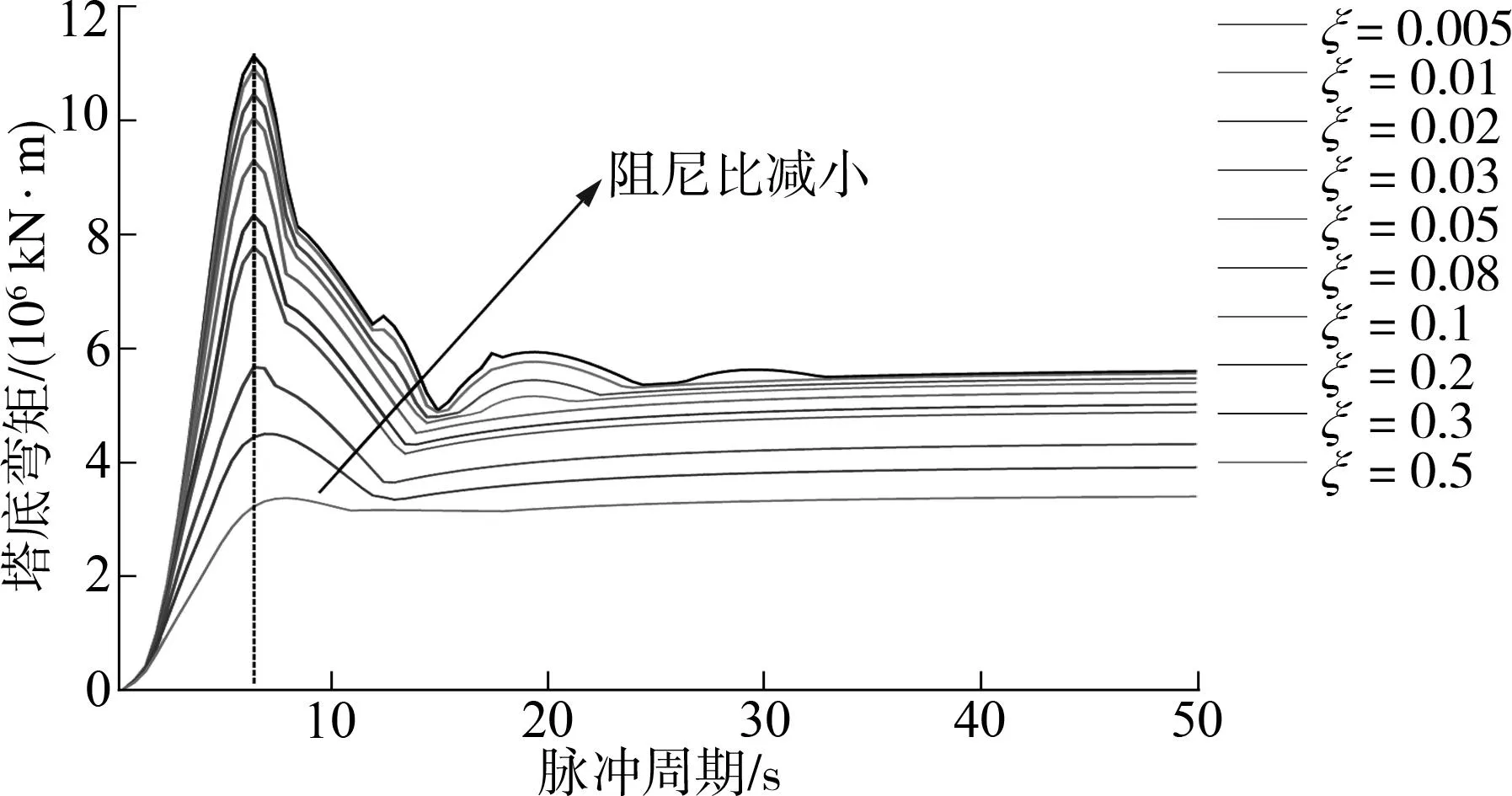
(b)独塔斜拉桥图8　塔底弯矩与脉冲周期的关系Fig.8　Relationship between tower bottom moment and pulse period

(a)双塔斜拉桥

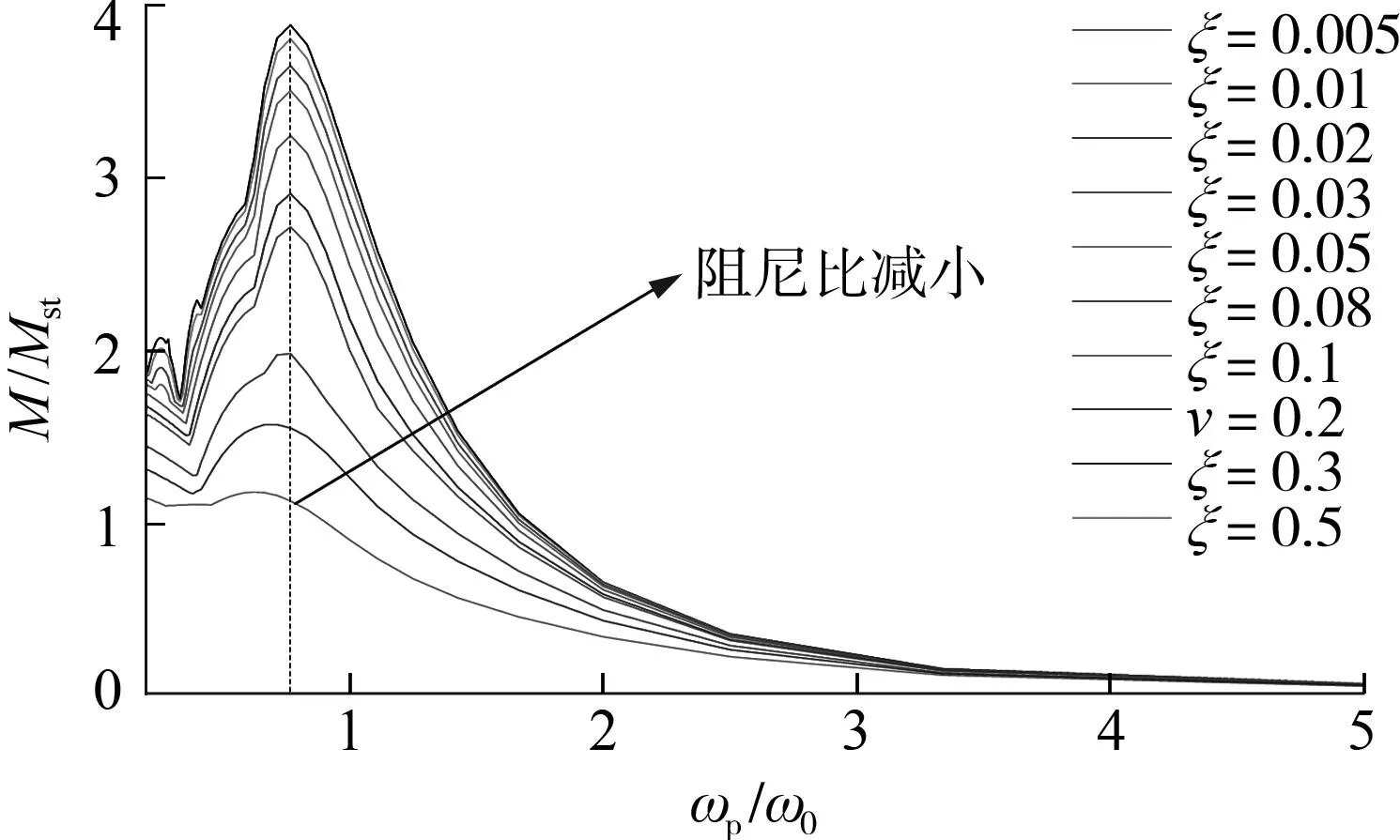
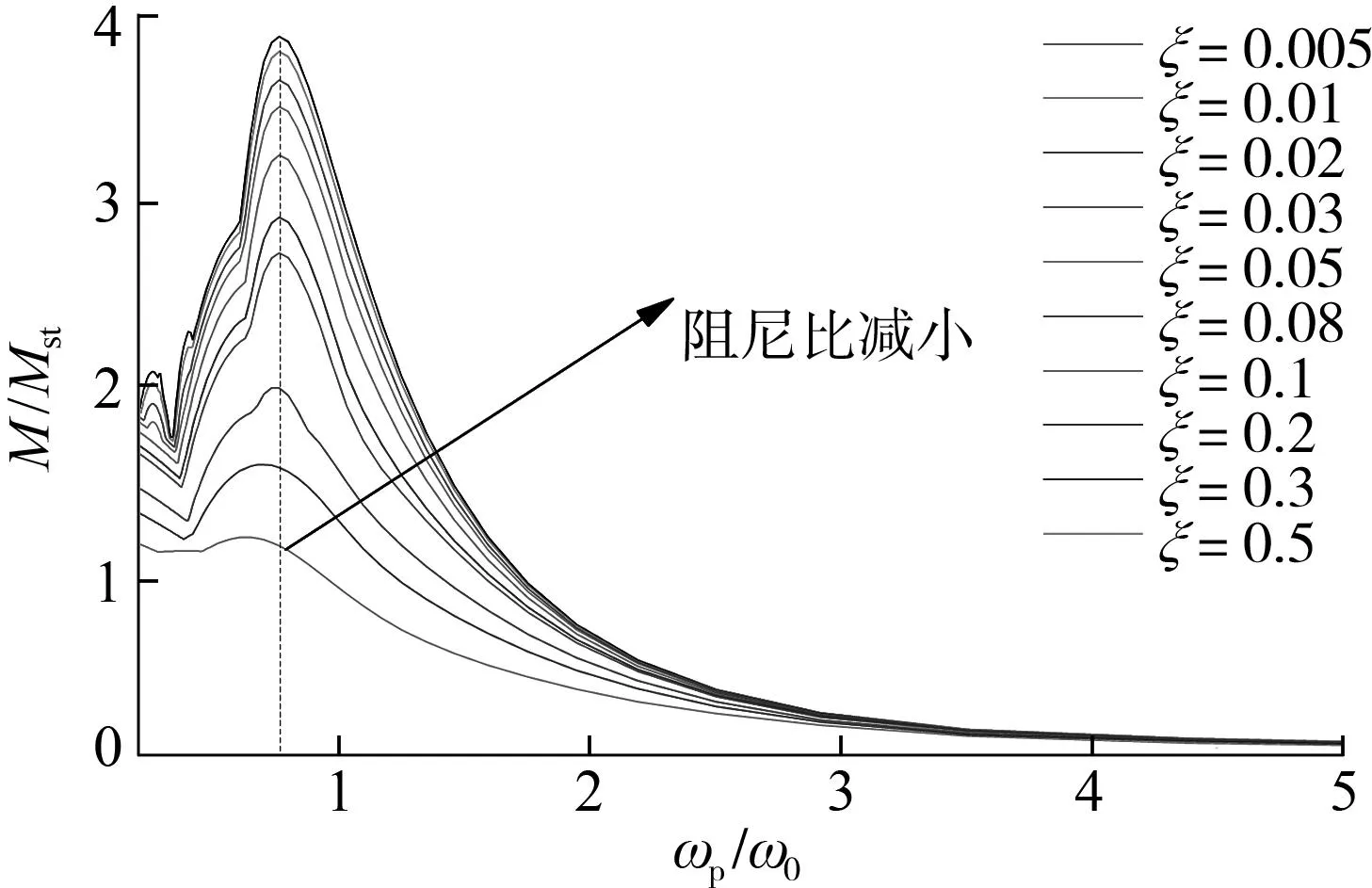
(b)独塔斜拉桥图9　放大系数与频率比的关系Fig .9　Relationship between amplification factor and frequency ratio

从图9看出，随着阻尼比减小，塔底弯矩(或塔顶位移)放大系数增大，在频率比达到0.75左右，放大系数取得峰值；在小于这个比值时，放大系数随着频率比增大而增大；在大于这个比值时，放大系数随频率的增加而逐渐减小，当频率比超过3之后影响基本可忽略.换言之，当斜拉桥基本周期约为脉冲周期的0.75倍时，脉冲对结构产生的动力响应最大.

6结论

斜拉桥由于大都采用漂浮体系或半漂浮体系，地震低频成分对其起主要作用，这对于以脉冲为主导的近断层地震动作用下的斜拉桥的地震响应研究提供了可行的简化计算方法，研究表明：

(1)应用简化脉冲模型可以快捷近似计算塔底弯矩和塔顶位移，有效提高了斜拉桥抗震初步设计的效率.

(2)当脉冲的频率与结构振动频率比值在0.75左右时，结构的地震响应最为剧烈，当频率比超过3之后影响基本可忽略；结构地震响应或放大系数随阻尼比减小而增大.

(3)近断层脉冲富含低频成分，对大跨长周期结构的地震响应具有明显的放大效应.位于断层附近的斜拉桥抗震设计时，应视脉冲频率与斜拉桥基本振动频率之间的关系，考虑脉冲对塔底响应的放大效应.

参考文献:

[1]BipinShrestha.Seismicresponseoflongspancable-stayedbridgetonear-faultverticalgroundmotions[J].JournalofCivilEngineering,2015,19(1):180-187.

[2]ChioccarelliE,IervolinoI.Near-sourceseismichazardanddesignscenarios[J].EarthquakeEngineering&StructuralDynamics,2013,42(4):603-622.

[3]ChampionC,LielA.Theeffectofnear-faultdirectivityonbuildingseismiccollapserisk[J].EarthquakeEngineering&StructuralDynamics,2012,41(10):1391-1409.

[4]AdanurS,AltuniikAC,BayraktarA,etal.Comparisonofnear-faultandfar-faultgroundmotioneffectsongeometricallynonlinearearthquakebehaviorofsuspensionbridges[J].Naturalhazards,2012,64(1):593-614.

[5]AlaviB,KrawinklerH.Considerationofnear-faultgroundmotioneffectsinseismicdesign[C]∥Proceedingsofthe12thWorldConferenceonEarthquakeEngineering.Auckland:[s.n.],2000:No.2665.

[6]SasaniM,BerteroVV.Importanceofseverepulse-typegroundmotionsinperformance-basedengineering:historicalandcriticalreview[C]∥Proceedingsofthe12thWorldConferenceonEarthquakeEngineering.Auckland:[s.n.],2000:No.1302.

[7]SomervillePG.Developmentofanimprovedrepresentationofnearfaultgroundmotions[C]∥ProceedingsofSMIP98SeminaronUtilizationofStrong-MotionData.Kacramento:CaliforniaDivisionofMinersandGeology,1998:1-20.

[8]MakrisN,ChangSP.Effectofviscous,viscoplasticandfrictiondampingontheresponseofseismicisolatedstructures[J].EarthquakeEngineering&StructuralDynamics,2000,29(1):85-107.

[9]MenunC,FuQ.Ananalyticalmodelfornear-faultgroundmotionsandtheresponseofSDOFsystems[C]∥ProceedingsofEarthquakeEngineeringResearchInstituteeds.SeventhUSNationalConferenceonEarthquakeEngineering.Boston,Massachusetts:MiraDigitalPublishing,2002.

[10]李新乐,朱晞.近断层地震动等效速度脉冲研究[J].地震学报,2005,26(6):634-643.

LiXin-le,Zhuxi.Researchonequivalentvelocitypulseofnearfaultground[J].JournalofEarthquake,2005,26(6):634-643.

[11]袁万城,闫冬.斜拉桥纵飘频率简化计算方法[J].同济大学学报:自然科学版,2005,33(11):1423-1427.

YuanWan-cheng,YanDong.Simplifiedcalculationalmethodoffloatingfrequencyforcable-stayedbridge[J].JournalofTongjiUniversity:NaturalScienceEdition,2005,33(11):1423-1427.

[12]徐艳,段昕智,李建中.强震作用下斜拉桥纵桥向非线性地震反应分析[J].华南理工大学学报:自然科学版,2012,40(6):132-138.

XuYan,DuanXin-zhi,LiJian-zhong.Analysisofnonlinearseismicresponseofcable-stayedbridgesubjectedtolongitudinalstronggroundmotions[J].JournalofSouthChinaUniversityofTechnology:NaturalScienceEdlition,2012,40(6),132-138

[13]颜海泉,王君杰.飘浮体系斜拉桥纵向抗震计算的单塔模型[J].地震工程与工程振动,2007,27(4):80-86.

YanHai-quan,WangJun-jie.Atowermodelforseismicresponsepredictionoffloatingcable-stayedbridgeinlongitudinaldirection[J].EarthquakeEngineeringandEngineeringVibration,2007,27(4):80-86.

[14]ChopraAK.Dynamicsofstructures:theoryandapplicationstoearthquakeengineering[M].3thed.America:Prentice-Hall,Inc,2007:389-391.

[15]嵇冬冰.混凝土斜拉桥横桥向振动台试验研究[D].上海:同济大学土木工程学院,2014.

文章编号：1000-565X(2015)02-0041-07

收稿日期：2014-08-05

*基金项目：国家“973”计划项目(2013CB036302);国家自然科学基金资助项目(51478338)

Foundation items： Supported by the National Program on Key Basic Research Program of China(2013CB036302)and the National Natural Science Foundation of China(51478338)

作者简介：徐艳(1976-)，女，博士，副研究员,主要从事桥梁抗震研究．E-mail: yanxu@tongji.edu.cn

中图分类号：U442.5+5

doi：10.3969/j.issn.1000-565X.2015.02.007

SimplifiedCalculationofLongitudinalSeismicResponseofCable-Stayed
BridgesSubjectedtoPulsedGroundMotions

Xu YanHuang Yong-fuLi Jian-zhong

(StateKeyLaboratoryofDisasterReductioninCivilEngineering,TongjiUniversity,Shanghai200092,China)

Abstract:In order to investigate the effect of near-fault pulsed ground motions on cable-stayed bridges, the characteristics of near-fault pulsed ground motions are analyzed and are fitted to different numerical pulse models by means of the least square method. Then, the complex cable-stayed bridge is simplified into a system with single degree of freedom in longitudinal direction via the equivalent modal method, and the dynamic differential equations of the cable-stayed bridge subjected to near-fault pulsed ground motions are therefore established and solved. Meanwhile, the analytical relationships between the top displacement as well as the bottom moment of the tower and the period as well as the amplitude of the pulse velocity are obtained to further reveal the general law of bridge seismic responses varying with pulse parameters. Finally, finite element analyses of both single-tower and double-tower cable-stayed bridges are carried out to verify the accuracy of the proposed method. The results indicate that the method is of simplicity, feasibility and an acceptable error.

Key words:cable-stayed bridge; seismic response; near-fault ground motion; pulse model; equivalent modal method; least square method