矩形截面型材三维拉弯成形的回弹预测*
2015-12-25滕菲梁继才张万喜王雪高嵩
滕菲 梁继才 张万喜 王雪 高嵩
(1.大连理工大学 汽车工程学院∥工业装备结构分析国家重点实验室, 辽宁 大连 116024;
2.吉林大学 材料科学与工程学院, 吉林 长春 130022)
矩形截面型材三维拉弯成形的回弹预测*
滕菲1梁继才1张万喜1王雪2高嵩1
(1.大连理工大学 汽车工程学院∥工业装备结构分析国家重点实验室, 辽宁 大连 116024;
2.吉林大学 材料科学与工程学院, 吉林 长春 130022)
摘要:设计了用于三维拉弯成形的、可重构的柔性模具,并采用支持向量回归机和有限元模拟对柔性三维拉弯成形的回弹进行预测.使用有限元法分析了对回弹量影响较大的6个因素(包括材料参数、几何参数和工艺参数),以及它们对回弹的影响趋势.选用这6个参数设计有限元三维拉弯模拟实验,并用模拟结果训练和检验支持向量回归机回弹预测模型.通过与广泛应用的神经网络预测方法的预测值和有限元模拟试验结果的比较,检验该回弹预测模型的准确性.研究发现,该模型与神经网络相比具有更高的准确度,在试验中根据该模型预测的回弹量对模具型面进行相应的补偿,可以有效地减小回弹和形状偏差.
关键词:型材;回弹预测;支持向量回归机;人工神经网络;三维拉弯成形
随着汽车轻量化的发展,铝型材已广泛应用于汽车行业当中[1-2].在铝型材拉弯成形过程中,回弹是影响成形质量的主要原因,其引起的与目标形状的偏差导致装配困难[3-4].因此,研究拉弯成形过程中回弹产生的原因及对回弹量进行预测具有重要的意义[5-6].
Clausen等[7]探讨了拉伸力和应变硬化性能对回弹的影响规律.Miller等[8]基于截面在拉弯成形过程中长度不变的假设,提出了一种简单的回弹预测模型,并证明较大的拉力能够减小回弹.Oliveira等[9]研究发现,在回弹预测过程中应变硬化的影响没有前人研究的那么大.Yu等[10]研究了工艺参数对尺寸精度的影响,如压边力和拉力等.Panthi等[11]采用有限元法对板料成形回弹进行预测,研究了材料性质和几何参数对回弹的影响,结果表明,回弹量随弹性模量的增大而减小,随屈服应力增大而增大.以上这些研究表明,回弹随拉弯过程中拉力的增大而减小,在拉弯成形过程中影响回弹量的主要因素包括材料性质、几何参数和工艺参数.
有限元是较为常用的预测回弹的方法,但它需要消耗大量的时间,通过训练和结合神经网络能够很好地解决这一问题.人工神经网络(ANN)结合有限元方法已广泛应用于回弹预测当中.Kazan等[12]提出了一种用于折弯过程中预测回弹的神经网络模型,方法中采用有限元模拟得到的数据训练该模型.Nasrollahi等[13]提出了一种采用神经网络和有限元法预测带孔薄板回弹的模型.Song等[14]基于人工神经网络方法建立了T型截面梁弯曲过程的回弹预测模型.用于回归预测的支持向量机叫做支持向量回归(SVR),目前已广泛应用于诸多领域,它能够实现少量样本的回归求解.龙玲等[15]采用SVR建立了起皱和破裂的非线性拟合,研究证实了SVR的准确性高于ANN;Liu等[16]提出了基于SVR的非线性问题代理模型,该模型的准确性和有效性已被证实;Singh等[17]采用SVR预测了冲压拉深过程中杯壁的厚度变化,研究表明采用SVR模型预测精度高于ANN.这些研究表明,SVR比传统技术ANN具有更强的泛化能力,并且能够更好地解决非线性预测问题,同时SVR能够预测板料成形等复杂问题.但是,SVR很少应用于铝型材拉弯成形回弹的预测.
文中首先介绍了柔性三维拉弯模具和SVR原理;然后通过有限元模拟确认对回弹影响较大的因素;采用这些因素作为设计变量进行有限元三维拉弯模拟,建立型材柔性三维拉弯成形回弹预测的SVR模型,其中预测模型的训练样本是有限元数值模拟结果;最后,对三维拉弯成形SVR回弹预测模型的精度进行验证,将SVR模型和ANN模型的预测结果和试验结果进行比较,检验SVR模型的预测精度,并用试验对采用SVR预测模型得到的回弹量对柔性三维拉弯模具进行型面补偿后减小回弹的有效性进行验证.
1柔性模具和SVR
1.1柔性三维拉弯模具
柔性拉弯成形模具由若干单元体组成,这些单元体代替了传统的整体模具.柔性拉弯模具的型面可通过调节单元体的位移和旋转成形滑块实现重构.每个基本体由支架、垂直导轨、导向滑块、成形面滑块,以及限位元件等构成,并安装在可以前后移动的独立支架上,如图1所示.型材三维拉弯成形过程首先实现水平面的弯曲,然后再进行垂直面弯曲.
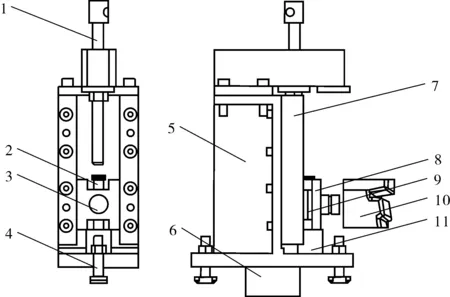
(a)前视图 (b)左视图
图1基本体示意图
Fig.1Diagramoftheunit-body
1—高度控制螺杆;2—垂直销轴;3—水平销轴;4—螺栓;5—支架;6—导向键;7—垂直导轨;8—成形面滑块底板;9—导向滑块;10—多点模具;11—垫块
1.2回弹评价
常见的回弹评价方法有3种:曲率半径的变化量、回弹角的变化量和回弹法向位移的变化量,如图2所示.很多研究者采用法向位移的变化作为衡量回弹大小的指标.但是该方法适用于二维拉弯,而不适用于三维拉弯.三维拉弯是在水平面和垂直面都进行拉弯成形,故采用法向位移不能完整地表示出回弹的大小.文中针对三维拉弯成形的特点,采用水平面拉弯成形和垂直面拉弯成形的回弹角来表征回弹量.回弹角通过以下公式计算:
δ=θ-θ0
(1)
式中,θ为变形区域回弹后的圆心角,θ0为变形区域回弹前的圆心角,
(2)
(3)
R0为目标曲率半径,R为回弹后的曲率半径,xs、ys分别为回弹后变形区域末端节点的水平面内坐标.

图2 回弹量评价Fig.2 Springback evaluation
1.3支持向量机
支持向量机是基于统计学理论和结构风险最小化原则建立起来的新机器学习方法.支持向量机主要解决非线性问题,通过核函数把初始空间非线性问题转化成高维特征空间内的线性问题,然后在高维特征空间内对线性问题求解[18].支持向量机用于解决回归问题时称为支持向量机回归(SVR),SVR能够较好地解决小样本求解问题.SVR的目的是为了寻找一决策函数y=
(1)给定一个用于训练的样本集合
(4)
(xi∈Rn,yi∈R,i=1,...,l)
为了推断任意一个输入值x所对应的输出值y,需要根据式(4)在实数集R上寻找一个实值函数g(x).这类问题属于在n维空间Rn内的回归问题,回归问题分为线性回归和非线性回归问题,而三维拉弯成形过程回弹预测属于非线性回归.
(2)选择恰当的核函数K(x,xi),以及适当的精度ε和惩罚函数C.通常情况下采用多项式核函数和高斯径向基核函数.
多项式核函数:
K(x,xi)=[(x,xi)+1]d
(5)
高斯径向基核函数:
(6)
(3)构造并求解凸二次规划问题:
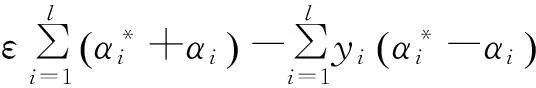
(7)


(4)构造决策函数:
(8)


(9)
2有限元分析
2.1正交试验
型材拉弯成形回弹量主要受到材料参数、几何参数和工艺参数的影响.根据不同条件对回弹影响的分析,文中选取弹性模量E、屈服应力σ0、水平弯曲角度θh、垂直弯曲角度θv、预拉量δ0和补拉量δ1作为正交试验的因子,这些因子的变化范围如表1所示,各个因子在各自范围内选取5个水平.如果采用六因素五水平全面的试验方法,则需要进行56组试验,利用正交试验设计安排试验方案,能够显著提高试验效率,减少试验数量,并能够保证结果的合理性.因此,使用L25(56)正交表设计试验方案,通过数值模拟获得训练和检验数据.为了增加样本数量,选择成形效果良好的另外15组数据增加到样本中,那么就有40组样本用于SVR模型的训练和检验.
表1正交试验设计输入参数及其变化范围
Table1Inputparametersandtheirrangesfororthogonaldesign
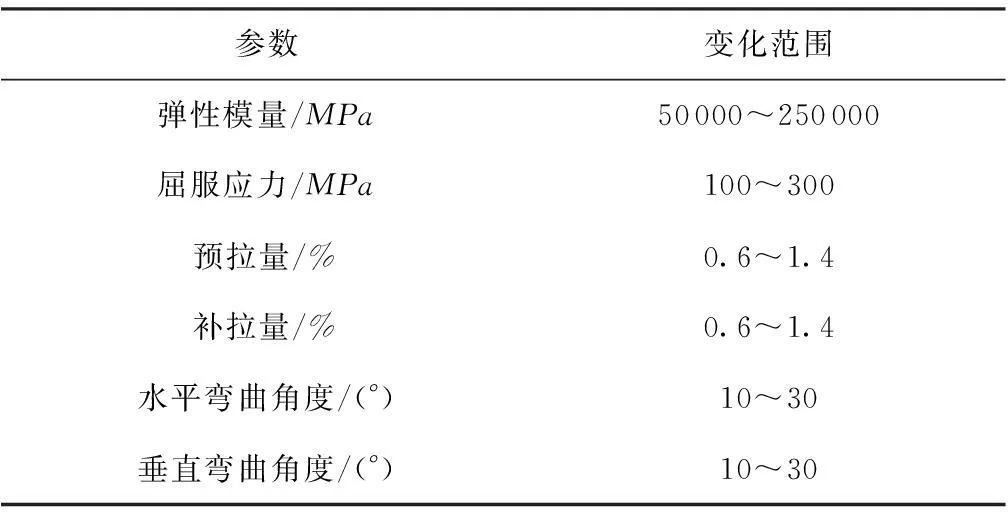
参数变化范围弹性模量/MPa50000~250000屈服应力/MPa100~300预拉量/%0.6~1.4补拉量/%0.6~1.4水平弯曲角度/(°)10~30垂直弯曲角度/(°)10~30
2.2有限元模拟
数值模拟采用商业有限元软件ABAQUS,其中ABAQUS/Explicit模块模拟型材三维拉弯成形过程,ABAQUS/Standard模块模拟卸载回弹过程.考虑到边界条件和加载的对称性,取1/2模型进行模拟.图3为柔性三维拉弯成形装配图,由铝型材、若干单元体和夹钳组成.型材的长度为1m,柔性三维拉弯成形模具由16组单元体构成,型材目标弯曲半径为1500mm,其他参数根据正交试验进行设计.考虑到夹钳和单元体的变形不需要计算,为了提高计算速度,夹钳和基本体采用离散刚体壳单元,夹钳与型材绑定,型材选用离散实体单元.图4为型材回弹前后形状对比,图中黑色图形为回弹前的型材,绿色图形为回弹后的型材,在型材的端点处回弹较明显.
在三维拉弯成形过程中,首先完成水平面弯曲,然后进行垂直面弯曲.在预拉阶段,模具固定,通过对夹钳施加轴向位移实现型材的拉伸;在弯曲阶段,采用位移-时间曲线以1m/s速率控制型材逐步弯曲与模具成形面贴合;最后,施加切向位移对型材进行补拉.面与面的接触采用罚函数法.

图3 有限元模型装配图Fig.3 Assembling-up of the simulation model

图4 三维拉弯成形回弹Fig.4 Springback of three-dimension stretch bending
为了获得样本数据需要进行40组有限元模拟,其中20组用于训练SVR和ANN模型,剩余20组用于检验SVR和ANN模型的准确性.各因素的极差如表2所示.
表2水平面和垂直面各因素极差
Table2Rangeofvariousfactorsinhorizontalandverticalplanes

因素极差水平面垂直面E0.6850.402σ00.2230.103δ00.2790.207δ10.2320.232θh0.8820.126θv0.2090.736
由表2可以看出,对于水平面拉弯回弹,影响较大的是水平弯曲角度、弹性模量和预拉量,而补拉量、屈服应力和垂直方向弯曲角度对回弹影响相对较小;对于垂直面回弹,影响较大的是垂直方向弯曲角度、弹性模量和补拉量;而预拉量、水平弯曲角度和屈服应力对回弹影响相对较小.
3回弹预测
3.1SVR模型的训练
表1中的6组参数设为输入参数,水平方向回弹角θhs和垂直方向回弹角θvs作为输出参数.由表1可以看出,不同参数的输入值存在较大的量级差异,训练和检验数据需进行归一化处理.归一化能有效改善预测精度,使数据分布在较小的范围内,训练和检验数据经归一化后处于[-1,1]之间.
核函数的选择对最终的预测结果有很大的影响,文中采用台湾大学开发的Libsvm-3.17程序包进行回归预测.SVR分为epsilon-SVR和nu-SVR,核函数有3种类型:线性、多项式和径向基函数(RBF).为了找到SVR类型和核函数的最佳组合,对不同的组合进行研究,结果如表3所示.研究发现,采用epsilon-SVR和径向基核函数的回弹预测模型具有更高的准确性.
表3SVR类型和核函数的组合结果
Table3ResultsofcombinationofSVRclassandkernelfunction

SVR核函数迭代次数均方误差相关系数epsilon-SVR线性1110.1098970.745366epsilon-SVR多项式210.2809370.201485epsilon-SVR径向基20340.0901590.744558nu-SVR线性310.2112220.662721nu-SVR多项式200.3091940.269683nu-SVR径向基1800.1887480.461243
在采用SVR模型预测回弹之前,需要确定惩罚系数C和参数g的大小.C和g是平衡模型的适应性和预测准确性的重要参数,对模型最终的预测结果有很大影响.在不同的C和g值组合中,通常采用交叉验证方法找出具有最高预测精度的组合.文中采用gridregression函数寻找最佳的C和g值组合,根据研究,C=512、g=1时预测结果精度最高,均方误差为0.03426.在40组样本中随即选取20组作为SVR模型的训练样本.
3.2SVR模型的检验
采用剩余样本对SVR预测模型进行检验.为了检验SVR算法回弹预测的精度,文中选用目前已在回弹预测方面得到广泛应用的人工神经网络算法(ANN)进行对比.神经网络有3层网络结构,包括输入层、隐含层和输出层,其中隐含层包含56个节点,输出层2个节点.选用与训练SVR模型相同的数据对神经网络模型进行训练,训练误差控制在10-5内.图5为SVR和ANN模型预测结果的对比,可以看出采用SVR算法预测回弹值与实验数据更加接近;表4和5分别为两个方向上回弹量的误差比较,从均方误差的对比中可以看出SVR模型预测回弹的准确性高于ANN模型.

(a)水平面回弹角预测

(b)垂直面回弹角预测 图5 SVR和ANN模型的预测结果对比Fig.5 Comparison of springback prediction results obtained by SVR and ANN
表4水平方向回弹角的误差对比
Table4Comparisonoferrorsofspringbackangleinthehorizontaldirection

预测模型均值最小值最大值平均误差SVR0.702870.102851.133180.11353ANN0.612030.398610.783590.30698
表5垂直方向回弹角的误差对比
Table5Comparisonoferrorsofspringbackangleintheverticaldirection

预测模型均值最小值最大值平均误差SVR0.951790.636681.231860.12543ANN1.073260.542441.526480.18556
4试验检验
文中通过两组柔性三维拉弯成形试验,检验SVR模型对回弹的预测精度.一组试验用于检验预测模型的准确性,另一组试验根据SVR模型的回弹预测值,对模具型面进行相应的补偿,从而达到减小回弹的目的.
矩形截面型材采用AA6082铝合金,其弹性模量E为71GPa,泊松比ν为0.345,屈服应力σ0为139.5MPa,假定材料服从Hill’48各向异性屈服准则,F=1.625,G=1.476,H=0.524,N=4.047.表6为预测模型的输入数据,表7为分别采用
SVR和ANN模型的预测结果和误差.基于相同的输入数据,通过真实的柔性三维拉弯成形试验获得的水平方向回弹角和垂直方向回弹角分别为0.685°和0.861°;表7所示的两种模型的预测误差再次证明SVR预测结果更加准确.
表6预测模型的输入数据
Table6Inputofthepredictionmodels

E/GPaσ0/MPaδ0/%δ1/%θh/°θv/°71139.50.80.83030
表7模型预测结果及误差
Table7Predictionresultsanderrorsofthemodels

模型预测θhs/(°)预测θvs/(°)水平回弹角误差/%垂直回弹角误差/%SVR0.6562830.8163624.235.14ANN0.8726451.13756427.332.1
基于两种模型对回弹的预测结果,对模具型面进行相应的补偿,补偿后对型材进行柔性三维拉弯成形试验,从而获得根据两种模型补偿后的形状偏差.两种模型补偿后的型材形状偏差如图6所示.

图6 模具补偿后形状误差的对比Fig.6 Comparison of shape error after the die shape compensation
由图6可以看出,根据ANN预测对模具补偿后的形状偏差大于SVR预测补偿后的偏差.由此可知,SVR回弹补偿比ANN准确,从而证明SVR的回弹预测比ANN的回弹预测精度高.
5结语
通过设计正交试验进行有限元模拟测试6组参数(包括材料参数、几何参数和工艺参数)对三维拉弯成形回弹影响大小进行分析.分析证明这些参数对水平面回弹角与垂直面的回弹角影响程度不同.设计了选用这些参数作为输入参数、对柔性三维拉弯成形进行回弹预测的SVR模型,并将该模型与ANN模型的预测精度进行对比.实验结果证明,采用SVR预测模型能够实现对三维拉弯成形回弹的预测,且预测精度高于ANN.采用SVR模型回弹预测值对三维拉弯成形试验的模具型面进行相应补偿,能够有效减小回弹和形状偏差.
参考文献:
[1]李落星,周佳,张辉.车身用铝、镁合金先进挤压成形技术及应用[J].机械工程学报,2012,48(18):35-43.
LiLuo-xing,ZhouJia,Zhanghui.Advancedextrusiontechnologyandapplicationofaluminummagnesiumalloyforvehiclebody[J].JournalofMechanicalEngineering,2012,48(12):35-43.
[2]马铭图,李志刚,易红亮,等.汽车轻量化及铝合金的应用[J].世界有色金属,2006,10:10-14.
MaMing-tu,LiZhi-gang,YiHong-liang,etal.Polarizationoflight-weightedcarsandapplicationofaluminumalloys[J].WorldNonferrousMetals,2006,10:10-14.
[3]梁继才,滕菲,高嵩,等.柔性三维拉弯成形模具型面修正关键技术的研究[J].机械工程学报,2013,49(17):187-192.
LiangJi-cai,TengFei,GaoSong,etal.Keytechnologiesresearchontheiterativedie-faceadjustmentintheformingprocessofflexiblethree-dimensionalstretch-bending[J].JournalofMechanicalEngineering,2013,49(17):187-192.
[4]梁继才,滕菲,高嵩,等.矩形铝型材柔性三维拉弯工艺的多目标优化[J].华南理工大学学报:自然科学版,2013,41(9):143-148.
LiangJi-cai,TengFei,GaoSong,etal.Multi-objectiveoptimizationofflexiblethree-dimensionalstretch-bendingformingprocessrectangularhollowaluminumprofiles[J].JournalofSouthChinaUniversityofTechnology:NaturalScienceEdition,2013,41(9):143-148.
[5]徐义,李落星,李光耀,等.型材弯曲工艺的现状及发展前景[J].塑性工程学报,2008,15(3):61-70.
XuYi,LiLuo-xing,LiGuang-yao,etal.Extrusionbending:method,applicationandrecentdevelopment[J].JournalofPlasticityEngineering,2008,15(3):61-70.
[6]刁可山,周贤宾,李晓星,等.矩形截面型材拉弯成形[J].北京航空航天大学学报,2005,31(2):134-137.
DiaoKe-shan,ZhouXian-bin,LiXiao-xing,etal.Stretchbendingofaluminumextrusion[J].JournalofBeijingUniversityofAeronauticsandAstronautics,2005,31(2):134-137.
[7]ClausenArildH,HopperstadOddS,LangsethMagnus.Sensitivityofmodelparametersinstretchbendingofaluminumextrusions[J].InternationalJournalofMechanicalSciences,2001,43:427-453.
[8]MillerJE,KyriakidesS,CoronaE.Onbend-stretchformingofaluminumextrudedtubes-Ⅱ:analysis[J].InternationalJournalofMechanicalSciences,2001,43:1319-1338.
[9]OliveiraMC,AlvesJL,ChaparroB.M,etal.Studyontheinfluenceofwork-hardeningmodelinginspringbacksimulationaccuracyofV-freebending[J].InternationalJournalofPlasticity,2007,23:516-543.
[10]YuZhong-qi,LinZhong-qin.NumericalanalysisofdimensionprecisionofU-shapedaluminumprofilerotaystretchbending[J].TransactionsofNonferrousMetalsSocietyofChina,2007,17:581-585.
[11]PanthiK,RamakrishnanN,AhmedMeraj,etal.Finiteelementanalysisofsheetmetalbendingprocesstopredictthespringback[J].MaterialandDesign,2010,31:657-662.
[12]KazanR,FiratM,TiryakiAE.Predictionofspringbackinwipe-bendingprocessofsheetmetalusingneuralnetworks[J].MaterialsandDesign,2009,30(2):418-423.
[13]NasrollahiV,ArezooB.Predictionofspringbackinsheetmetalcomponentswithholesonthebendingarea,usingexperiments,finiteelementandneuralnetworks[J].MaterialsandDesign,2012,36:331-336.
[14]SongY,YuZ.SpringbackpredictioninT-sectionbeambendingprocessusingneuralnetworksandfiniteelementmethod[J].ArchiveofCivilandMechanicalEngineering,2013,3:229-241.
[15]龙玲,殷国富,宋超,等.基于支持向量机的随机聚焦搜索算法优化冲压成形工艺[J].四川大学学报:工程科学版,2012,44(5):220-225.
LongLing,YinGuo-fu,SongChao,etal.ApplicationofstochasticfocusingsearchalgorithmbasedonSVMinoptimizationofsheetmetalformingprocess[J].JournalofSichuanUniversity:EngineeringScienceEdition,2012,44(5):220-225.
[16]LiuYu-lin,ChenWen-liang,DingLi-ping,etal.Responsesurfacemethodologybasedonsupportvectorregressionforpolygonblankshapeoptimizationdesign[J].InternationalJournalofAdvancedManufacturingTechnology,2013,66:1397-1405.
[17]SinghSwadenshKumar,GuptaAmitKumar.Applicationofsupportvectorregressioninpredictingthicknessstrainsinhydro-mechanicaldeepdrawingandcomparisonwithANNandFEM[J].CIRPJournalofManufacturingScienceandTechnology,2010,3:66-72.
[18]丁世非,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J]. 电子科技大学学报,2011,40(1):2-10.
DingShi-fei,QiBing-juan,TanHong-yan.Anoverviewontheoryandalgorithmofsupportvectormachines[J].JournalofUniversityofElectronicandScienceandTechnologyofChina,2011,40(1):2-10.
文章编号:1000-565X(2015)02-0107-07
收稿日期:2014-08-06
*基金项目:国家工信部重点产业振兴和改造技术专项(吉工信投资[2011]350)
Foundation item:Supported by the National Ministry Key Industrial Revitalization and Transformation of Special Technology(Ministry of Jilin Province([2011]350)
作者简介:滕菲(1985-),女,博士生,主要从事汽车材料加工研究.E-mail: tengfei325@126.com
中图分类号:TG386
doi:10.3969/j.issn.1000-565X.2015.02.016
SpringbackPredictionofRectangularProfilesDuringThree-Dimension
StretchBendingForming
Teng Fei1Liang Ji-cai1Zhang Wan-xi1Wang Xue2Gao Song1
(1.SchoolofAutomotiveEngineering//StateKeyLaboratoryofStructuralAnalysisforIndustrialEquipment,
DalianUniversityofTechnology,Dalian116024,Liaoning,China; 2.CollegeofMaterialsScienceandEngineering,
JilinUniversity,Changchun130022,Jilin,China)
Abstract:In this paper, first, a reconfigurable flexible die for the three-dimension stretch bending forming is designed, and the springback of profiles during the forming is predicted by means of the support vector regression and the finite element simulation. Then, six factors that greatly affect the springback magnitude (including material parameters, geometrical parameters and process parameters) are analyzed by using the finite element method, and their impact trends on the springback are also investigated. Moreover, these six factors are employed to design a simulation of three-dimension finite-element stretch bending, and the simulated results are used to train and test the springback prediction model based on the support vector regression machine. Finally, for the purpose of verifying the proposed apringback prediction model, the predicted results are compared with those obtained by the widely-used neural network forecasting method and the finite element simulation. It is found that the proposed model is more accurate than the neural network-based method, and that, in experiments, suitable compensations to the die shape according to the springback value predicted by the model may effectively reduce the springback and the shape deviation.
Key words:profile; springback prediction; support vector regression machine; artificial neural networks; three-dimension stretch bending forming
