关于模糊数贴近度问题的研究

雷一鸣，代兵，包玉娥

（内蒙古民族大学数学学院，内蒙古通辽028043）

关于模糊数贴近度问题的研究

雷一鸣，代兵，包玉娥

（内蒙古民族大学数学学院，内蒙古通辽028043）

利用模糊集和区间数的贴近度理论，讨论了模糊数的贴近度问题.通过区间数与模糊数之间的关系，根据区间数贴近度的一般表示形式，给出了构造一些模糊数贴近度的具体计算公式的方法；并通过实例说明了所得到的贴近度公式的有效性和实用性，解决了常用贴近度公式所不能解决的问题.

区间数；模糊数；贴近度

1　引言

贴近度是不确定性数学理论及其应用中的重要概念之一，在模式识别、图象处理以及决策分析等领域中，具有广泛的应用.在不确定性数学理论中，关于模糊集的贴近度，早在1983年汪培庄教授提出了模糊集贴近度的概念［1］.从此，贴近度成为模糊数学研究领域中的一个有力工具.针对实际问题的需要，很多学者根据贴近度的公理化定义构建了多种模糊集贴近度公式［2-7］，为解决实际问题提供了合理有效的方法.本文在文献［8］中利用模糊集的贴近度理论，讨论了有关区间数贴近度的表示规律，给出了两种区间数贴近度的一般表示形式；并举例说明了根据区间数贴近度的一般表示形式可以构造多种贴近度公式.

模糊数是实数域上的一类特殊模糊集，在模糊分析学及其应用研究中起着非常重要的作用.在实际应用中，经常用模糊数来表示所属性决策领域中的许多决策信息［9-11］.因此，研究模糊数的贴近度理论及其应用问题也具有重要的理论意义和实际应用价值.由于区间数和模糊数的应用实际上均为属性值为实数的信息系统在维度上的化简.因此本文在文献［8］的基础上，利用模糊集和区间数的贴近度理论研究了模糊数的贴近度问题，并得到了一些区间数贴近度诱导出的模糊数贴近度的具体计算公式.

2　预备知识

设R为实数集，则模糊集u：R→［0，1］称为模糊数［12］，如果u是正规的，凸的上半连续的，且支集是紧集.模糊数全体构成的空间称为模糊数空间，记为F0.实数集R上的模糊集全体记为F（R），则F0⊂F（R）.

将模糊集贴近度的公理化定义［2］，限制在F（R）的子集F0上，就得到下面模糊数贴近度的公理化定义.

定义2.1设u，v，w∈F0，若映射N：F0×F0→［0，1］；（u，v）→N（u，v）满足下列条件：

（1）N（u，v）=N（v，u）；

（2）N（u，v）=1⇔u=v；

（3）u≤v≤w⇒N（u，w）≤N（u，v）且N（u，w）≤N（v，w），

则称N（u，v）为模糊数u与v的贴近度.

分别为区间数a的期望值与宽度.

定义2.2［8］设a，b，c∈［R］，若映射N：［R］×［R］→［0，1］；（a，b）→N（a，b）满足条件：

（1）N（a，b）=N（b，a）；

（2）N（a，b）=1⇔a=b；

（3）a⊆b⊆c⇒N（a，c）≤N（a，b）且N（a，c）≤N（b，c），

则称N（a，b）为模糊数a与b的贴近度.

定理2.1［8］设函数N：［R］×［R］→［0，1］，对任意a，b∈［R］，为

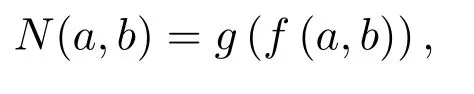
满足如下条件：

（1）f（a，b）=f（b，a）；

（2）f（a，b）=0⇔a=b；

（3）a⊆b⊆c⇒f（a，c）≥f（a，b）且f（a，c）≥f（b，c），

则N（a，b）=g（f（a，b））为区间数a与b的贴近度.

3　主要结果

下面利用区间数的贴近度理论讨论模糊数的贴近度问题，并给出计算模糊数贴近度的一些具体计算公式.

定理3.1设函数

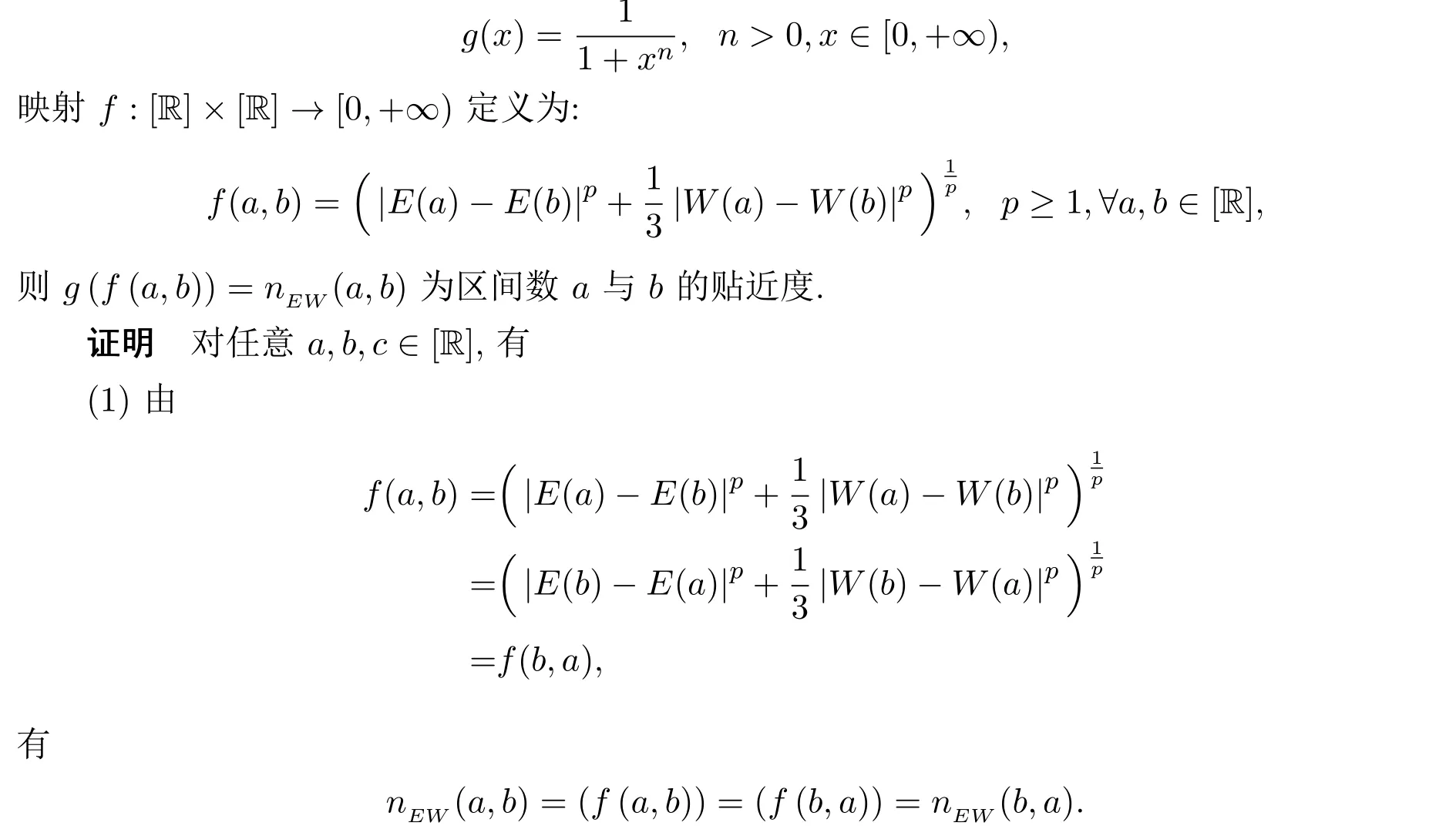
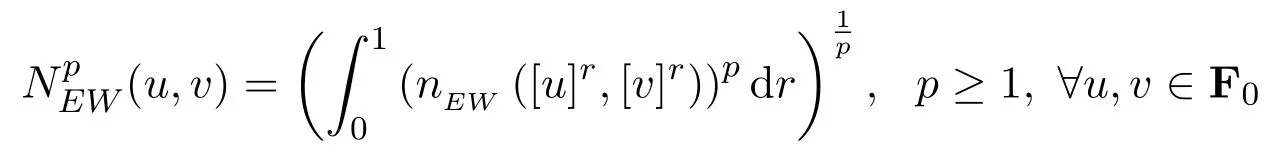
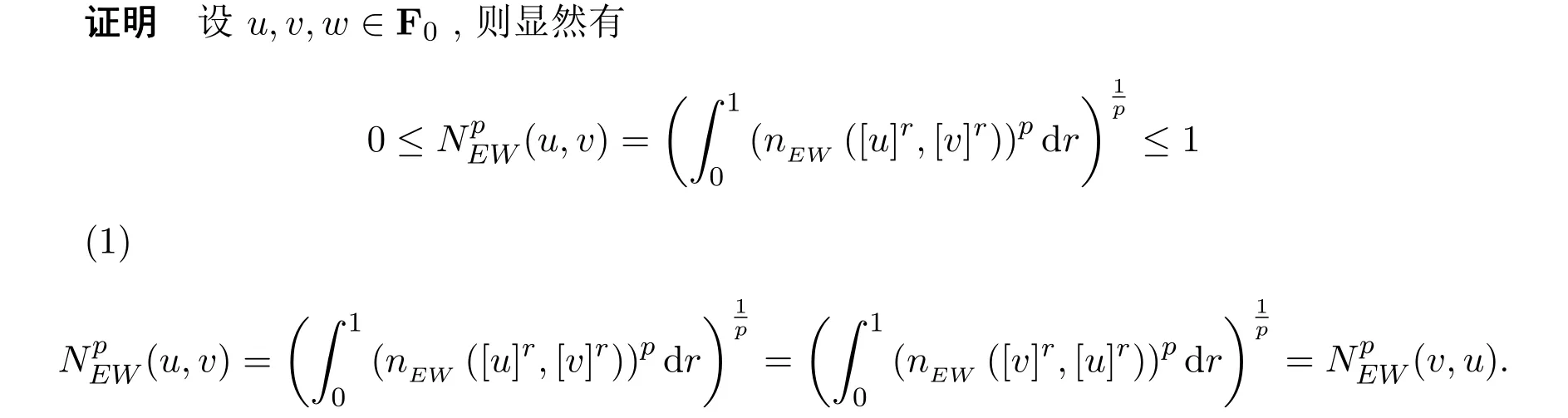
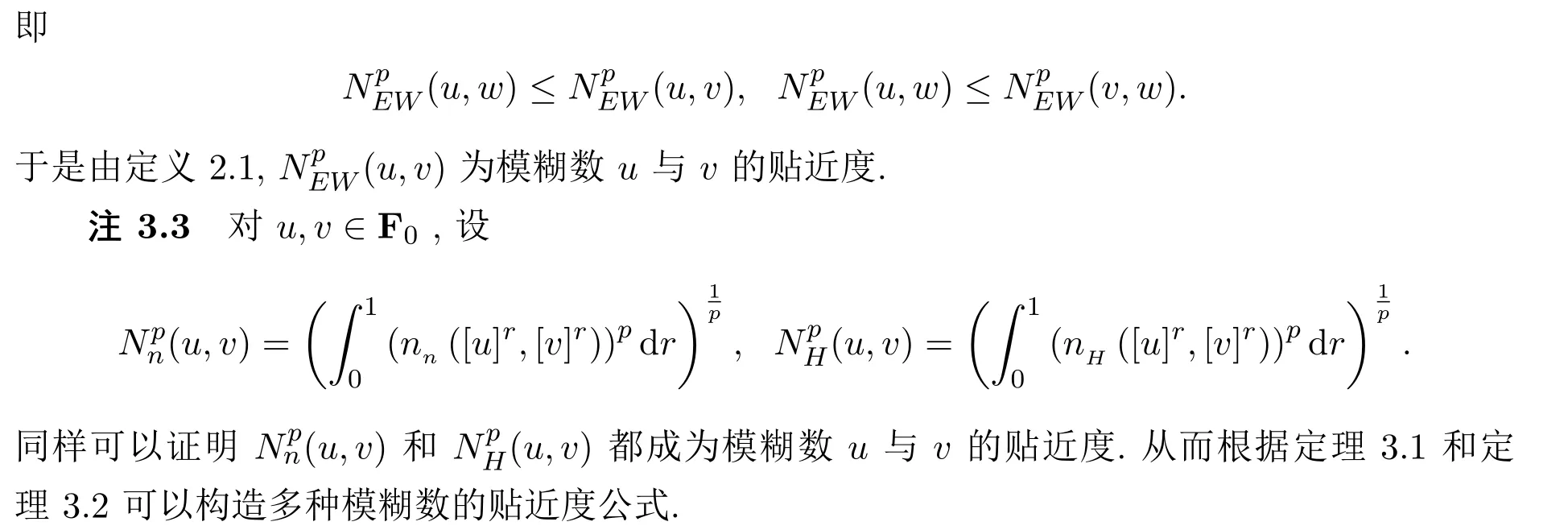
例3.1设u=〈0，1，2〉，v=〈1，2，4〉，w=〈5，6，8，10〉，求

三个模糊数的隶属函数图如图3.1所示.

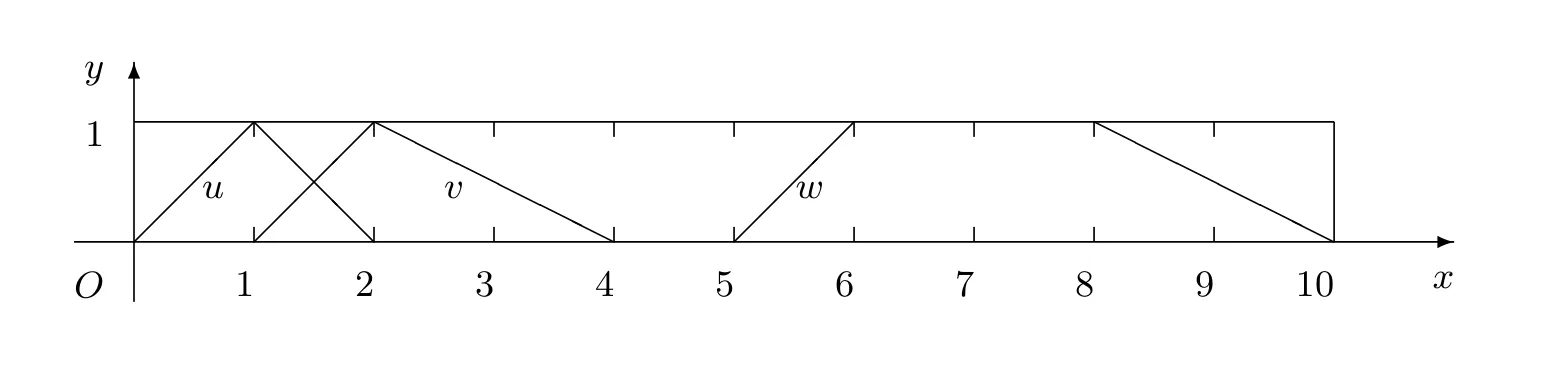
图3　.1u=〈0，1，2〉，u=〈1，2，4〉，u=〈5，6，8，10〉

由图3.1也可以直观地看出u与v的贴近程度比u与w的程度大的多.三个模糊数u，v，w之间的贴近程度排序为：

如果把三个模糊数u，v，w看成是有限论域U=［0，10］上的三个模糊集，则通过Haming贴近度和Euclid贴近度公式分别计算u，v，w之间的贴近度得：

计算结果表明：三个模糊数u，v，w之间的贴近程度度排序为：

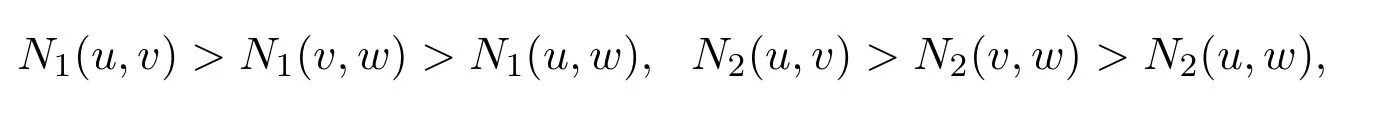
这与所引进的EW-型贴近度公式的计算结果是一致，即EW-型贴近度公式具有一定的适用性.

例3.2设u=〈0，1，2〉，v=〈1，2，3〉，u=〈5，6，8，10〉.

（1）将三个模糊数u，v，w看成是有限论域U=［0，10］上的三个模糊集，则通过Haming贴近度Euclid贴近度公式分别计算得：

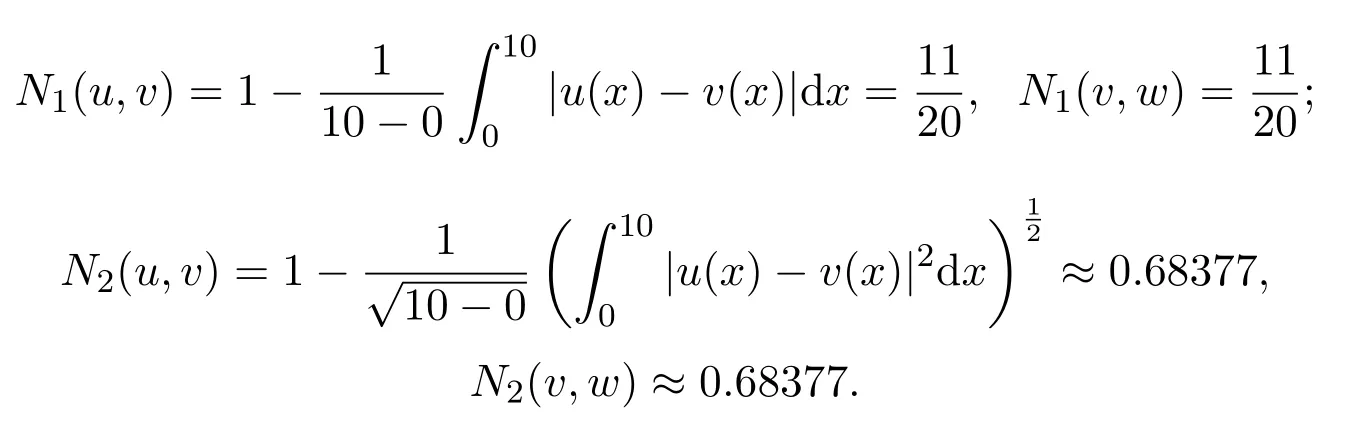
（2）用测度贴近度公式计算得：

三个模糊数u，v，w的隶属函数图如图3.2所示.

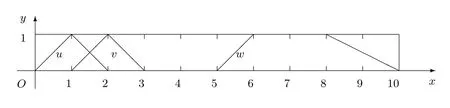
图3　.2u=〈0，1，2〉，v=〈1，2，3〉，u=〈5，6，8，10〉.

由图3.2，发现常用贴近度公式不能完全区分三个模糊数u，v，w之间的贴近程度.但是用引进的EW-型贴近度公式能解决此类问题.计算结果为：

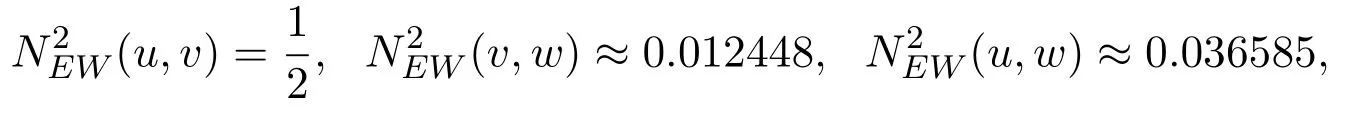
即贴近程度度排序为：

计算结果与直观看到的结果一样，这说明EW-型贴近度公式的有效性和实用性.

4　结论

模糊集的贴近度表示两个模糊集的贴近程度，在模式识别、模糊信息处理以及决策分析等领域中，具有广泛的应用.在实际应用中，经常用实数域上的一类特殊模糊集—模糊数来表示所属性决策领域中的许多决策信息等.模糊数又可以用一族区间数来刻划.因此，本文利用模糊集和区间数的贴近度理论，讨论了模糊数的贴近度问题.根据区间数与模糊数之间的关系，给出了构造一些模糊数贴近度的具体计算公式的方法.这些对模糊数的贴近度理论及其实际应用的研究提供了一种新的思想方法.

［1］汪培庄.模糊集合论及其应用［M］.上海：上海科学出版社，1983.

［2］罗承忠.模糊集引论［M］.北京：北京师范大学出版社，2009.

［3］Lui X C.Entropy，distance measure and similarity measure of fuzzy sets and their relations［J］.Fuzzy Sets and Systems，1992，52：305-318.

［4］曾文艺，李洪兴.模糊度与贴近度的关系研究［J］.系统工程与实践，1999，6：76-79.

［5］崔宝珍，曾文艺.基于Hausdroff距离和Lp度量的直觉模糊集合贴近度的注记［J］.模糊系统与数学，2009，3：122-126.

［6］刘兆君.模糊集贴近度的一般表示形式［J］.数学的实践与认识，2009，18：163-169.

［7］李医民，王晓梅.基于Type-2模糊贴近度在生态上的应用［J］.数学的实践与认识，2010，20：74-82.

［8］彭晓芹，包玉娥，赵博.关于区间数贴近度的一般表示形式的研究［J］.数学的实践与认识，2014，22：258-262.

［9］徐泽水.基于期望值的模糊多属性决策法及其应用［J］.系统工程理论与实践，2004，1：109-119.

［10］兰蓉，范九伦.三角模糊数上的完备度量及其在决策中的应用［J］.系统工程学报，2010，3：314-319.

［11］Shu P W.Power average operators of trapezoidal intuitionistic fuzzy numbers and application to multiattribute group decision making［J］.Applied Mathematical Modelling，2013，37：4112-4126.

［12］Wu C X，Zhao Z T.Some notes on the characterization of compact sets of fuzzy sets with Lp metric［J］.Fuzzy Sets and Systems，2008，159：2104-2115.

［13］包玉娥，彭晓芹，赵博.基于期望值与宽度的区间数距离及其完备性［J］.模糊系统与数学，2013，27（6）：133-139.

［14］吴从炘，赵志涛，任雪昆.模糊分析学与特殊泛函空间［M］.哈尔滨：哈尔滨工业大学出版社，2013.

The research of degree of closeness about fuzzy numbers

Lei Yiming，Dai Bing，Bao Yu′e

（College of Mathematics，Inner Mongolia University for the Nationalities，Tongliao028043，China）

Degree of closeness about fuzzy numbers has been discussed by degree of closeness about fuzzy sets and interval numbers.According to the general expressions of degree of closeness about interval numbers and the connection of interval numbers and fuzzy numbers，some formulas of degree of closeness about fuzzy numbers has been structured.Then by examples，both availability and practicability of the formulas of degree of closeness about fuzzy numbers has been illustrated，and the formulas can apply when common formulas become useless in some circumstances.

interval numbers，fuzzy numbers，degree of closeness

O178

A

1008-5513（2015）06-0611-09

10.3969/j.issn.1008-5513.2015.06.009

2015-07-20.

国家自然科学基金（11461052）；内蒙古自然科学基金（2014MS0107）.

雷一鸣（1989-），硕士生，研究方向：模糊分析及其应用.

包玉娥（1962-），博士，教授，研究方向：不确定数学理论及应用.

2010 MSC：03E72