关于非齐次马氏链的一个定理

孙飞跃，杨卫国

（江苏大学理学院，江苏镇江212013）

关于非齐次马氏链的一个定理

孙飞跃，杨卫国

（江苏大学理学院，江苏镇江212013）

给出了Csiszar和Körner关于独立随机变量序列的一个定理的一个推广，该定理的推论是关于相对熵的，在统计假设检验及编码理论中起着重要的作用.利用非齐次马氏链的一个强大数定律将这个定理推广到非齐次马氏链上.

非齐次马氏链；强大数定律；几乎处处收敛

1　引言

马氏链作为描述一类实际问题的数学模型，在经济学、计算科学、随机服务系统等领域中具有重要地位.有关齐次马氏链的研究已经取得了丰硕且深刻的成果，例如：文献［1］研究了任意齐次树指标马氏链场的一类Shannon-Mcmillan定理；文献［2］应用齐次马氏链定量评估教学效果.齐次马氏链的研究已经形成了较完整的理论体系，而关于非齐次马氏链的极限性质已有不少研究，例如：文献［3］研究了可列非齐次马氏链的强大数定律，文献［4］研究了可列非齐次马氏链泛函的强大数定律，文献［5］研究了各种随机变量和马氏链的强偏差定理，但至今仍有待深入研究.本文首先给出Csiszar和Körner在著名的《Information Theory》［6］中关于独立随机变量序列的一个极限定理，该定理的推论是关于相对熵的.而相对熵是信息论中的一个重要内容，在统计假设检验及编码理论中起着重要的作用，作者利用非齐次马氏链的强大数定律将该定理推广到非齐次马氏链上.其结果是对文献［6］中相关定理的推广.

2　主要结果

设M1（x），M2（x），···是在字母集S=｛1，2，···，N｝上取值的一列正值函数，令

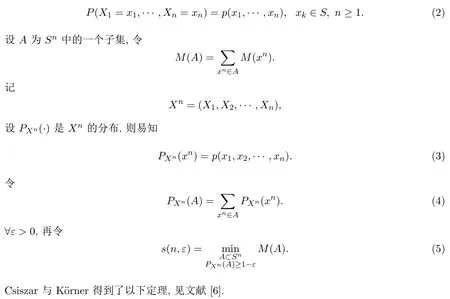
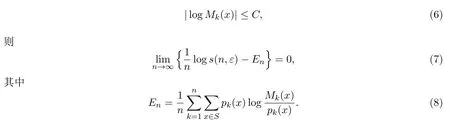
下面给出定理2.1的一个推论：

推论2.1设｛Xn，n≥1｝是在字母集S上取值的独立随机变量序列，设P和Q为两个概率测度，p（·），q（·）为S上的两个概率分布，设

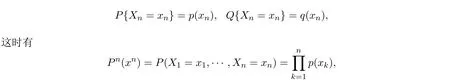
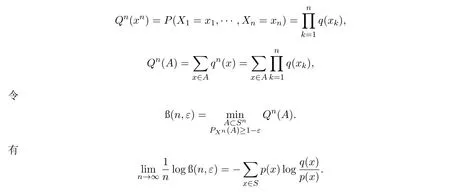
在信息论中，推论1的右边就是相对熵，也用D（p∥q）表示，相对熵是两个概率分布p和q差异的一种度量.在信息论中及解决随机选择系统问题中有重要作用，不少作者通过引进相对熵得出了随机选择系统和任意随机序列的若干强偏差和小偏差定理，解决了一系列实际问题［8-11］.

由定理2.1给出非齐次马氏链上的一个定理.

定理2.2设｛Xn，n≥1｝是在S=｛1，2，···，N｝中取值的非齐次马氏链，其初始分布和转移矩阵列分别为

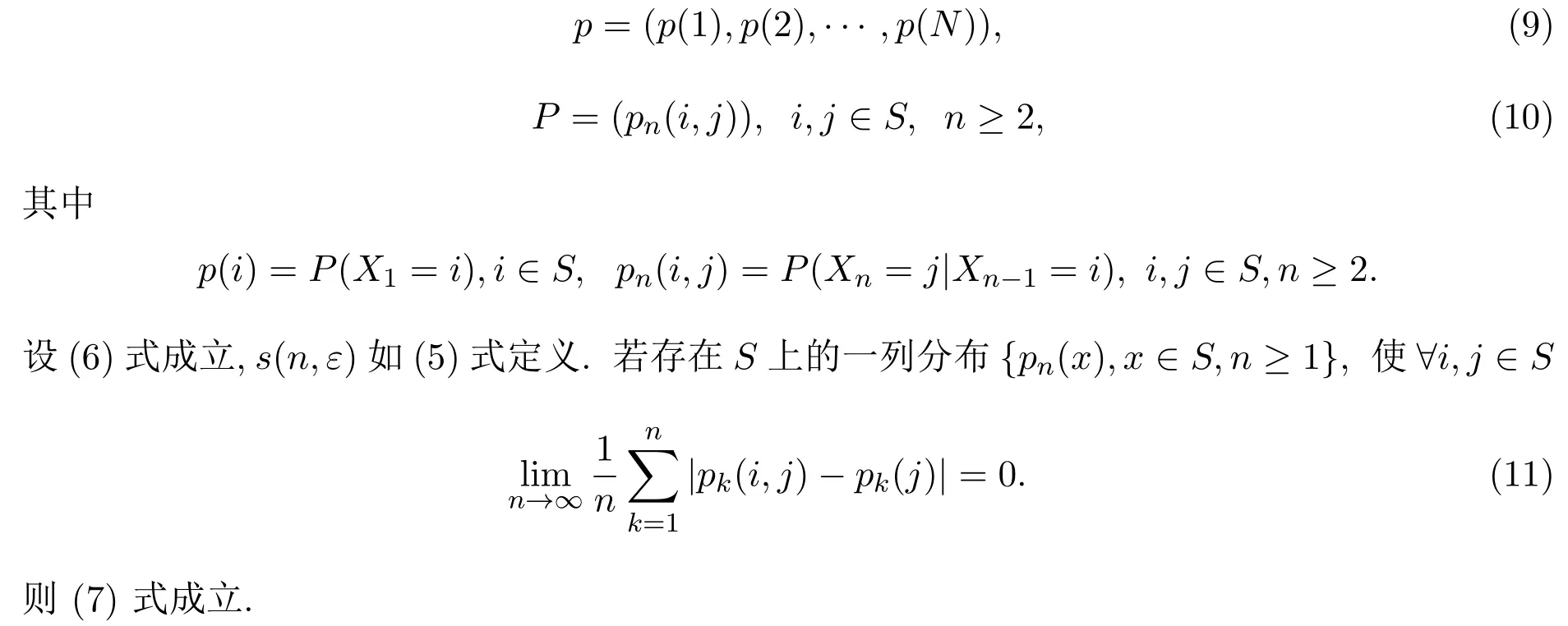
定理2.1是关于独立随机变量序列的极限定理，定理2.2将定理2.1的结论推广到了非齐次马氏链情形.

在证明本定理前首先给出几个引理.

引理2.1［7］设｛ak，k≥1｝是一有界非负数列，M为其一个上界，δ为正数，Nn（δ）表示此数列前n项大于δ的项的个数，则

成立的充要条件是：∀δ＞0

引理2.2设ϕ（x）是区间［a，b］上的连续函数，｛ak，k≥1｝与｛bk，k≥1｝是区间［a，b］上的两个数列，如果

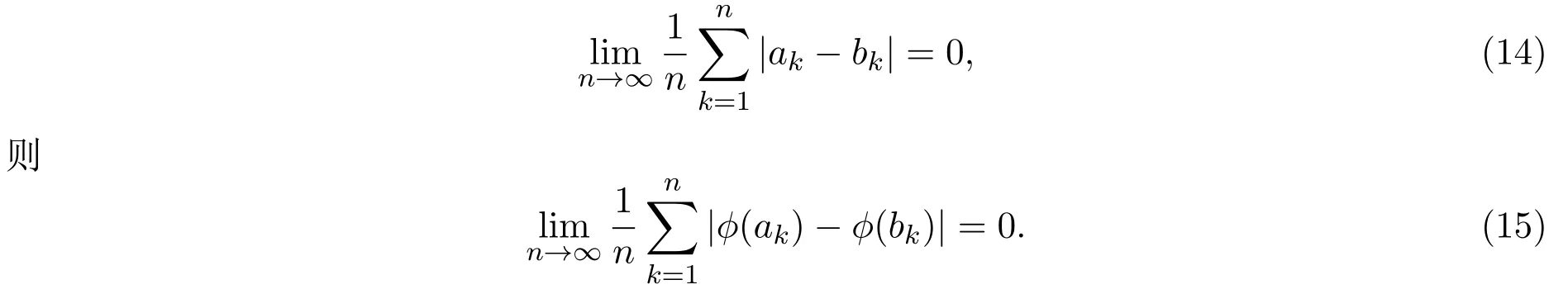
引理2.3［7］设｛Xn，n≥1｝是在S中取值的非齐次马氏链，其初始分布和转移矩阵列分别为（9）式和（10）式，fn（x，y）是定义在在S2上的二元函数，如果条件期望是几乎处处一致有界的，即存在一个常数M＞0，使

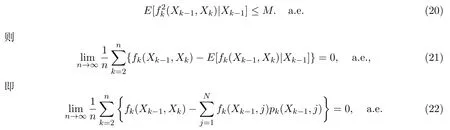
引理2.4设｛Xn，n≥1｝是在S中取值的非齐次马氏链，其初始分布和转移矩阵列分别为（9）式和（10）式，

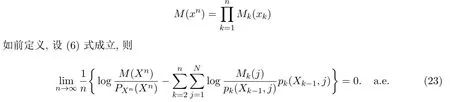
引理2.5设｛Xn，n≥1｝是在S中取值的非齐次马氏链，其初始分布和转移矩阵列分别为（9）式和（10）式，

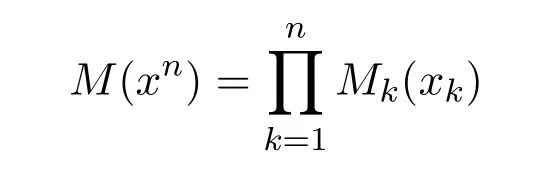
［1］方次军，王康康.任意齐次树指标马氏链场的一类Shannon-Mcmillan定理［J］.数学的实践与认识，2014，44（22）：223-231.

［2］陈裕宗.应用齐次马氏链定量评估教学效果［J］.厦门水产学院学报，1990，12（1）：60-64.

［3］刘文，杨卫国.可列非齐次马氏链的若干极限定理［J］.应用数学学报，1992，15（4）：479-489.

［4］刘文，刘国欣，陈志刚.可列非齐次马氏链泛函的一类强大数定律［J］.经济数学，1995，12（1）：1-8.

［5］王康康，杨卫国.任意随机序列关于广义几何分布的一类强偏差定理［J］.工程数学学报，2008，25（2）：239-244.

［6］Csiszar Imre，Körner Janos.Information Theory：Coding Theorems for Discrete Memoryless Systems［M］.New York：Academic Press，1981.

［7］刘文，杨卫国.关于非齐次马氏信源的渐进均分割性［J］.应用概率统计，1997，13（4）：359-366.

［8］赵静，魏杰，孙利民.样本相对熵率与一类随机选择系统的强偏差定理［J］.河北工业大学学报，2005，34（2）：110-114.

［9］刘文，杨卫国.关于Shnnon-McMillan定理的若干研究［J］.数学物理学报，1994，14（3）：337-345.

［10］范爱华.样本相对熵与相依随机序列的若干小偏差定理［J］.兰州大学学报，2008，44（1）：128-131.

［11］Shannon C E.A mathematical theory of communication［J］.USA Bell Systematic Technical Journal，1948，27：1-13.

A theorem for nonhomogeneous Markov chains

Sun Feiyue，Yang Weiguo
（Faculty of Science，Jiangsu University，Zhenjiang212013，China）

The purpose of this paper is to give a generalization of a theorem about independent random variables that has been provided by Csiszar and Körner.The corollary of this theorem is about relative entropy，which plays an important role in statistical hypothesis testing and coding theory.The theorem is generalized to the non-homogeneous Markov chains by using its strong law of large numbers.

non-homogeneous Markov chains，strong law of large numbers，a.e.convergence

O211.62

A

1008-5513（2015）06-0620-08

10.3969/j.issn.1008-5513.2015.06.010

2015-01-19.

国家自然科学基金（11071104）.

孙飞跃（1990-），硕士生，研究方向：马氏链.

2010 MSC：60J05