保体上上三角幂等矩阵的诱导映射

张隽，付丽，2，曹重光

（1.黑龙江大学数学科学学院，黑龙江哈尔滨150080；2.绥化学院信息工程学院，黑龙江绥化152061）

保体上上三角幂等矩阵的诱导映射

张隽1，付丽1，2，曹重光1

（1.黑龙江大学数学科学学院，黑龙江哈尔滨150080；2.绥化学院信息工程学院，黑龙江绥化152061）

假设Tm（D）是体D上所有上三角m×m矩阵的集合.首先分别给出诱导映射和保幂等性的定义.然后为了刻画Tm（D）的保幂等的诱导映射，提出类序列的概念，同时描述类序列的性质.最后，使用矩阵技术和初等方法，借助于分类讨论得到了Tm（D）的保幂等的诱导映射的一般形式并且给出了某些例子，用以解释某些结果之间的关系.

体；上三角矩阵；保幂等；诱导映射

1　引言

刻画矩阵集合保持某些性质的映射通常被称为矩阵保持问题研究.近年来，这方面的工作更感兴趣于映射没有线性和加法假定的情形［1-5］.本文研究的诱导映射，其实也是这类问题的一种.文献［6-7］是诱导映射导出问题的两个典型结果.

设D是一个体，Mm（D）及Tm（D）分别记D上所有m阶矩阵及所有m阶上三角阵的集合.设g是Mm（D）（Tm（D））到自身的映射，gij是D上的函数，其中i，j∈｛1，2，···，m｝.定义

则称g是由｛gij｝诱导的映射.简称Mm（D）（Tm（D））的诱导映射.

在本文中用K记Tm（D）中所有幂等阵（B2=B）的集合，令g是Tm（D）到自身的诱导映射，如果B∈K意味着g（B）∈K则称g保幂等.本文目的是刻画Tm（D）的保幂等的诱导映射.

用D∗记D中所有非0元的集合，Eij表示（i，j）位置是1，其余位置是零的矩阵.记［1，m］=｛1，2，···，m｝.

由于K中矩阵对角元必为1和0，又由于条件f（0）=0的需要，为叙述简洁方便，用Tm（D）仅表示对角元为1，0的上三角矩阵全体构成的集合.

现对Tm（D）诱导映射的定义中所涉及的m-1个函数，即g12，g23，···，gm-1m，定义如下的类集合：

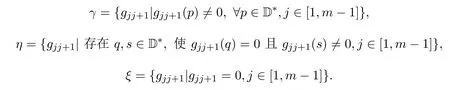
诱导映射g的类序列，即函数g12，g23，···，gm，m-1所属的类集合从左到右依次写成的一个序列.例如ξγηξηη为m=7时g的类序列，即有

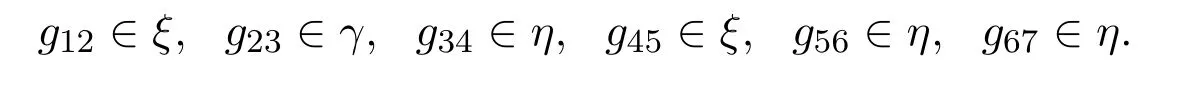
如果在g（0）=0的情况下，g是Tm（D）的保幂等的诱导映射，有如下的重要结果.

命题1.1设D为一个体，m为整数且m≥3，g（0）=0，其中g是Tm（F）的保幂等的映射，那么在g的类序列中不会出现相邻两类为ηγ，γη和ηη这三种情况.

下面将说明Tm（D）的每个保幂等的诱导映射g的类序列都对应着Tm（D）中矩阵的唯一分块写法.例如m=6时保幂等的g的类序列为ξηξγγ，则它对应着

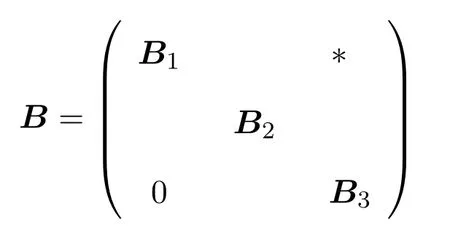
的分块写法，其中B1，B2和B3的阶数分别是1阶、2阶和3阶.又如m=9时保幂等的g的类序列若为γγγξηξξη，则它对应着

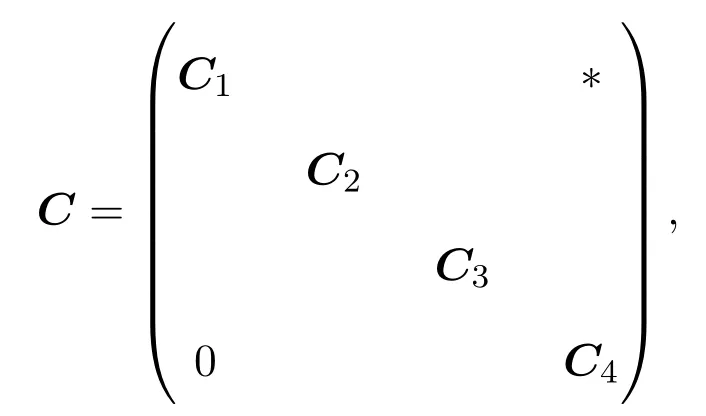
的分块写法，其中C1，C2，C3和C4的阶数分别为4阶，2阶，1阶和2阶.

一般地，满足g（0）=0的保幂等的导出映射g的类序列中ξ的个数若为s-1，则D的相应对角分块个数为s，即

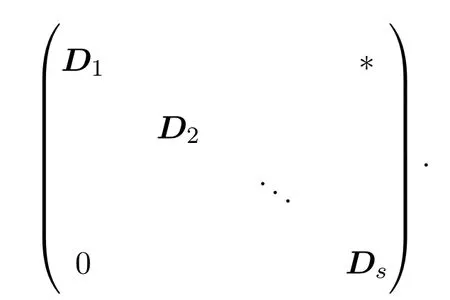
若类序列中第j个ξ与第j+1个ξ中间有非ξ类k个，则Dj+1是k+1阶的；若第1个ξ前面有k个非ξ类，则D1是k+1阶的；若第s-1个ξ后面有k个非ξ类，则Ds是k+1阶的，其中k≥0为整数.若g的类序列中无ξ，则D就是自己一块.

2　主要结果

定理2.1g为Tm（D）的诱导映射，g（0）=0，m≥3是一个整数，则g保幂等当且仅当

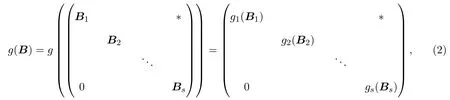
这里

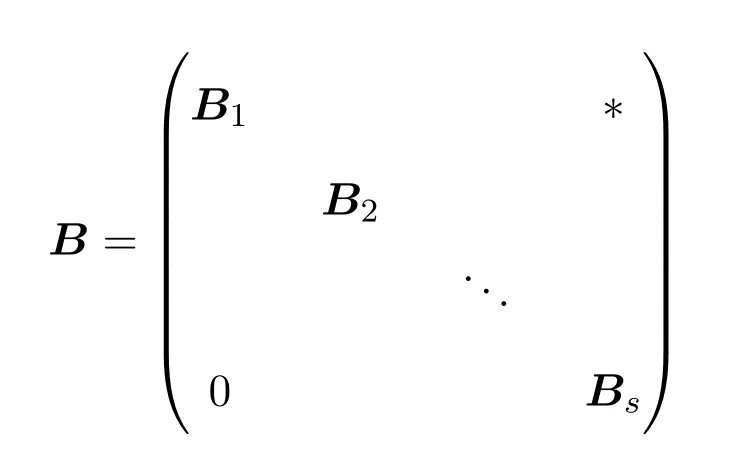
是g的类序列对应的B的唯一分块写法，其中B1，B2，···Bs的阶数分别是p1，p2，···，ps且m=p1+p2+···+ps，g1，···，gs分别为Tp1（D），···，Tps（D）保幂等的导出映射.

定理2.2D是一个体，g1为Tq（D）的诱导映射，g1（0）=0，又设ε=±1

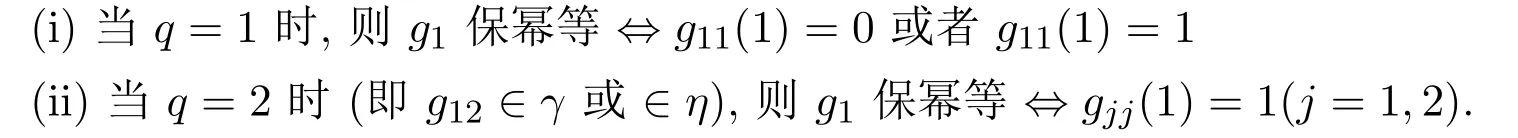
注记2.1如上定理2.1及定理2.2完整地刻画了m≥3时，Tm（D）的满足条件g（0）=0的保幂等的诱导映射.如果q≥4时，g1的形式（定理2.3中）称之为标准形式.容易验证当q=1，2，3时标准形式仍然满足定理2.3中的相应的充要条件，但反之未必.可以对q=3的情形举一个例子.令D是实数域，g11=g22=g33是恒等映射且

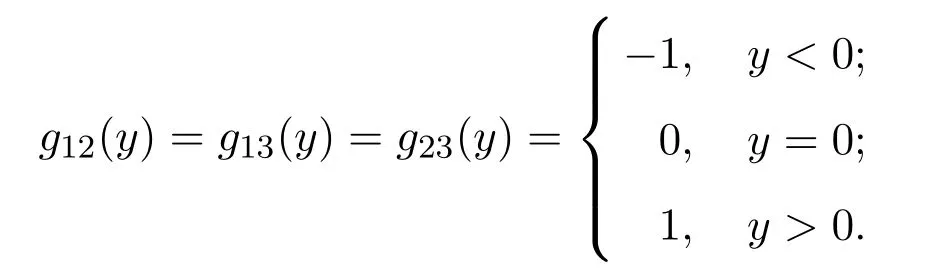
此时易验证g1满足定理2.3中q=3时的各项条件，但是g1并不是标准的，因为g1若是标准的，则应满足g12（2）=2g12（1），这与g12的定义相矛盾.

注记2.2如果去掉g（0）=0的条件，情况会相当复杂.

例如：令g（B）=C，∀B∈Tm（D），其中C∈K是任意固定的，则上述g是保幂等的诱导映射.

3　结语

诱导保持映射的研究结果尚不多，且多为在长方阵和方阵集合上研究.本文是对体上上三角矩阵诱导保持映射研究的一个有益的尝试，所用方法及所得结果具有一定的创新性，对后续研究有一个借鉴意义，其中提出类集合的概念对理论展开起了重要作用.

在本文结果中可以看到低维空间往往映射形式不具有标准性，于是举例说明其形式比标准形式更广泛就显得十分重要了（见注记2.1中例）.另外需指明的，条件f（0）=0对本文至关重要，如果去掉这一条件，实际上是一个开问题（见注记2.2）.

［1］Li C K，L Plevnik.Šemrl.Preservers of matrix pairs with a fixed inner product value［J］.Operators and Matrices，2012，6（3）：433-464.

［2］Cao C G，Ge Y L，Yao H M.Maps preserving classical adjoint of products of two matrices［J］.Linear and Multilinear Algebra，2013，61（12）：1593-1604.

［3］Huang L P.Geometry of Matrices over Ring［M］.Beijing：Science Press，2006.

［4］You H，Wang Z Y.k-Potence preserving maps without the linearty and surjectivity assumptions［J］.Linear Algebra Appl.，2007，426：238-254.

［5］Chooi W L，Ng W S.On classical adjoint-commuting mappings between matrix algebras［J］.Linear Algebra Appl.，2010，432：2589-2599.

［6］Liu S W，Zhang G D.Maps preserving rank 1 matrices over fields［J］.Journal of Natural Science of Heilongjiang University，2006，23（1）：138-140.

［7］Yang L，Ben X Z，Zhang M，et al.Induced maps on matrices over fields［J］.Abstract and Applied Analysis，vol.2014，Article ID 596796，5 pages，2014.

Induced maps preserving upper triangular idempotent matrices over skew fields

Zhang Jun1，Fu Li1，2，Cao Chongguang1

（1.School of Mathematical Science，Heilongjiang University，Harbin150080，China；2.School of Information Engineering，Suihua University，Suihua152061，China）

Suppose that Tm（D）is set of all m×m upper triangular matrices over skew field D.First，the paper gives the definition of induced map and preserving idempotence，respectively.And then，in order to characterize induced map preserving idempotence on Tm（D），the paper raises the concept of class-sequence and describes the properties of it.In the end，the paper uses matrix techniques and elementary methods and by classified discussion we get the general forms of induced maps preserving idempotence on Tm（D）and give some examples to illustrate relations between some results.

skew field，upper triangular matrix，preserving idempotence，induced map

O178

A

1008-5513（2015）06-0628-08

10.3969/j.issn.1008-5513.2015.06.011

2015-05-27.

国家自然科学基金（11371109）.

张隽（1991-），硕士生，研究方向：矩阵代数.

2010 MSC：15A04