Benny-Luke方程和Phi-4方程的精确行波解
2015-10-15陈立何姝琦董亚莹
陈立,何姝琦,董亚莹
(西北大学数学学院,陕西西安710127)
Benny-Luke方程和Phi-4方程的精确行波解
陈立,何姝琦,董亚莹
(西北大学数学学院,陕西西安710127)
运用了tanh-coth展开法,得到了Benny-Luke方程和Phi-4方程的一些新的精确行波解.同时该方法也可用于其他的非线性演化方程.
tanh-coth展开法;Benny-Luke方程;Phi-4方程;精确行波解
1 引言
非线性演化方程被广泛运用于现代科学中,非线性现象出现在科学和工程的许多分支中,例如等离子物理、流体力学、气体动力学、化学反应、生态、固体物理等给人留下深刻印象的研究领域.非线性演化方程经常用来描述孤立波运动,寻求非线性演化方程的精确很重要,因此精确行波解的探索变成非线性物理现象研究的一项重要任务.值得注意的是,观察到不存在独特的方法来解决所有非线性演化方程.由于这个原因,许多方法已被建立,例如Jacobi椭圆函数法[1]、齐次平衡法、MSE方法(Modified Simple Equation Method)[2]、展开法[3[5]、变分法、反散射方法、广田的双线性方法、tanh-coth展开法[69]、不变集方法[10]、不变子空间方法[11]、李群方法等.随着各种求解方法的出现,不但过去难于求解的方程得到解决,而且新的、具有重要物理意义的解不断被发现和应用,呈现出一个层出不穷的势头.
Malfliet首先介绍tanh展开法用于求解非线性偏微分方程,后来此方法被广泛运于求解非线性偏微分方程.Wazwaz将tanh展开法延拓为tanh-coth展开法.本文运用了tanh-coth展开法寻求Benny-Luke方程
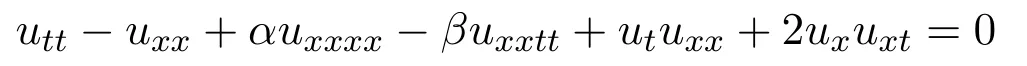
和Phi-4方程的精确行波解.本文安排如下:第2部分,介绍tanh-coth展开法;第3部分,将此方法应用于Benny-Luke方程,并得到该方程的一些新的精确行波解;第4部分,将此方法应用于Phi-4方程,并得到该方程的一些新的精确行波解;第5部分,将Benny-Luke方程和Phi-4方程的精确行波解做了物理解释和图像解释.最后,得知该方法在求解非线性演化方程的精确行波解时非常直观有效.
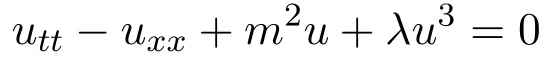
2 tanh-coth展开法

3 求解Benny-Luke方程
Benny-Luke方程是一个近似水波方程,适合在表面张力存在下描述双向水波传播,在物理等方面具有广泛的应用.在这一部分,将运用tanh-coth展开法来研究Benny-Luke方程

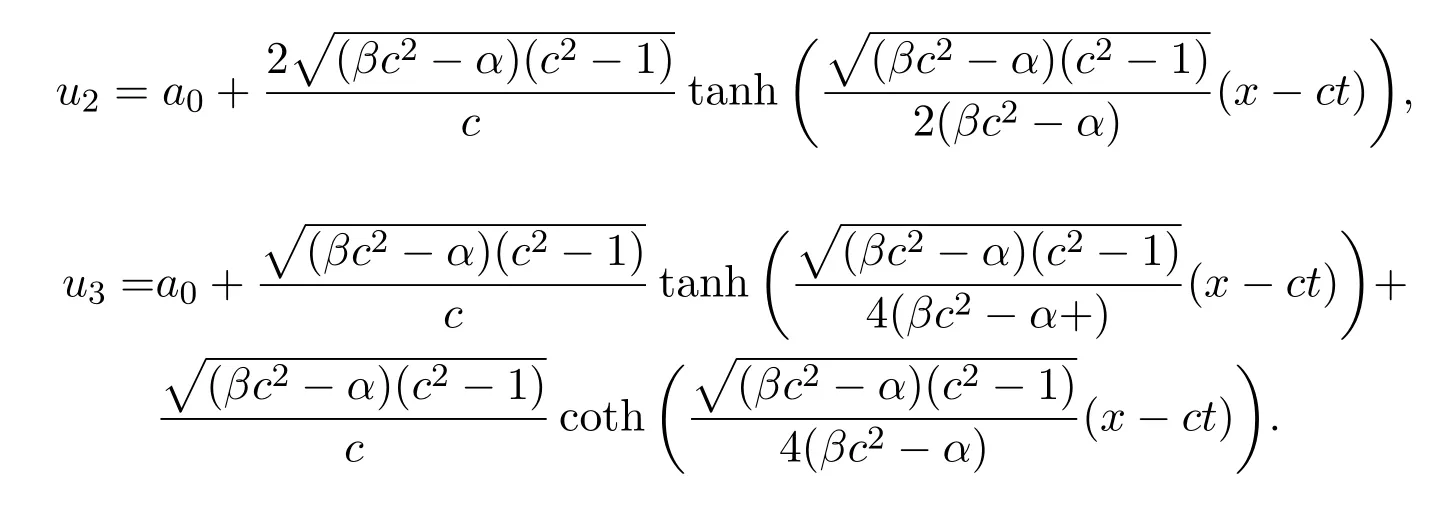
4 求解Phi-4方程
近几十年来,Phi-4方程在核物理和粒子物理占有很重要的地位.在这一部分,将运用tanh-coth展开法来研究Phi-4方程


5 物理解释和图像解释
在这一部分,将给出Benny-Luke方程和Phi-4方程的精确行波解的物理解释和图像解释.
本文第三部分运用tanh-coth展开法得到Benny-Luke方程的精确行波解u1,u2,u3.当取a0=1,α=1,β=1,(-10≤x≤10),(0≤t≤10)时,u1的图像如图1所示,图像1表示Benney-Luke方程的扭结型行波解,u2的图像如图2所示,图像2表示Benney-Luke方程的奇异扭结型行波解,u3的图像与u2的图像类似.
本文第四部分运用tanh-coth展开法得到Phi-4方程的精确行波解u1,u2,u3,u4,u5,u6,u7,u8.当取λ=-1.2,m=139,c=2,(-10≤x≤10),(0≤t≤10)时,u1的图像如图3所示,图像3表示Phi-4方程的多重周期解,u3的图像如图4所示,图像4表示Phi-4方程的奇异扭结型行波解,u2的图像与u1的图像类似,u4,u5,u6,u7,u8的图像与u3的图像类似.
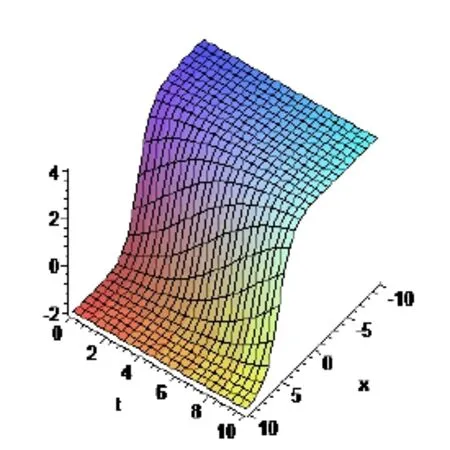
图1 Benny-Luke方程的解u1

图2 Benny-Luke方程的解u2

图3 Phi-4方程的解u1

图4 Phi-4方程的解u3
6 总结
本文运用tanh-coth展开法求解出Benny-Luke方程和Phi-4方程的一些新的行波解,从而丰富了方程的结果,有助于对方程所描述的物理现象进一步了解和研究.同时,这种方法也能够求解其他的非线性演化方程,也可以将双曲函数换成三角函数,同样能够得到一些方程的行波解.
[1]Ali A T.New generalized Jocobi ellipic function rational expansion method[J].Comput.Appl.Math.,2011,235:4117-4127.
[2]Akter J,Akbar M A.Exact solutions to the Benny-Luke equations and the Phi-4 equations by using modified simple equation method[J].Results in Physics,2015,5:125-130.
[3]Wang M,Li X,Zhang J.The(G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J].Phys.Lett.A,2008,372:417-423.
[4]Zayed E M E,Gepreel K A.The(G′/G)-expansion method for finding the travelling wave solutions of nonlinear evolution equations in mathematical physics[J].Math.Phys.,2009,50:013502-013514.
[5]Mohyud S T,Yildirim A,Saruaydin S.Numerical solitons of the improved Boussinesq equation[J].Int.J.Numer.Method H.,2011,21:822-827.
[6]Malfliet W.Solitary wave solutions of nonlinear wave equations[J].Am.J.Phys.,1992,60(7):650-654.
[7]Wazwaz A M.New travelling wave solutions to the Boussinesq and the Klein-Gordon Equations[J].Commun.Nonlinear Sci.Numer.Simulat.,2008,13:889-901.
[8]Wazwaz A M,Mona S M.A variety of exaction travelling wave solutions for the(2+1)-dimensional Boiti-Leon-Pempinelli equation[J].Appl.Math.Comput.,2010,217:1484-1490.
[9]Wazwaz A M.The tanh-coth method for solitons and kink solutions for nonlinear parabolic equations[J].Appl.Math.Comput.,2007,188:1467-1475.
[10]Dong Y Y,Zhang S L,Li S B.Invariant sets and solutions to a class of wave equations[J].Appl.Math.Comput.,2015,253:369-376.
[11]Qu G Z,Zhang S L,Li Y L.Third-order nonlinear differential operators preserving invariant subspaces of maximal dimension[J].Chin.Phys.B,2014,23:110202.
New travelling wave solutions to the Benny-Luke equation and the Phi-4 equations
Chen Li,He Shuqi,Dong Yaying
(College of Mathematics,Northwest University,Xi′an710127,China)
In this work,many new travelling wave solutions are established for the Benny-Luke equation and the Phi-4 equations.The tanh-coth method is used to generate these new solutions.The approach is also applicable to a large variety of nonlinear evolution equations.
the tanh-coth method,the Benny-Luke equation,the Phi-4 equations,travelling wave solutions
O175.29
A
1008-5513(2015)06-0604-07
10.3969/j.issn.1008-5513.2015.06.008
2015-06-16.
国家自然科学基金(11371293).
陈立(1989-),硕士生,研究方向:偏微分方程.
2010 MSC:35C07
