基于自适应参数校正策略求解SDP的Mehrotra型内点算法

黄方艳，张明望，黄正伟

（1.三峡大学理学院，湖北宜昌443002；2.三峡大学经济与管理学院，湖北宜昌443002）

基于自适应参数校正策略求解SDP的Mehrotra型内点算法

黄方艳1，张明望1，黄正伟2

（1.三峡大学理学院，湖北宜昌443002；2.三峡大学经济与管理学院，湖北宜昌443002）

最近，Salahi对线性规划提出了一个基于新的自适应参数校正策略的Mehrotra型预估-校正算法，该策略使其在不使用安全策略的情况下，证明了算法的多项式迭代复杂界.本文将这一算法推广到半定规划的情形.通过利用Zhang的对称化技术，得到了算法的多项式迭代复杂界，这与求解线性规划的相应算法有相同的迭代复杂性阶.

Mehrotra型算法；半定规划；迭代复杂性；对称化技术

1　引言

自Karmarkar［1］的开创性文章发表以来，内点算法成为最热门的研究对象之一，取得了大量的成果.1991年，Mehrotra［2］提出的预估-校正算法，也就是所谓的Mehrotra型预估-校正算法，是内点算法用于实际计算的一个里程碑式的成果.由于Mehrotra型预估―校正算法的优良的实际计算效果，Mehrotra型预估-校正算法及其变形算法成为一些著名内点算法软件包的基础［3-5］.遗憾的是关于Mehrotra型预估-校正算法的理论研究却很匮乏.直到2007年，在文献［6］中，Salahi等人通过分析一个极具启发性的数值实例发现：按照Mehrotra的预估-校正算法中中心参数的选择方法，为了使迭代点保持在特定邻域内，算法不得不作过多的小步迭代（步长难有下界），而迭代点保持在特定邻域内及步长有下界对证明算法的多项式复杂性及实际计算都非常重要.受此数值实例启示，他们在Mehrotra的算法中加入了“安全策略”来克服算法的缺陷，在此基础上提出了一个改进Mehrotra型预估-校正算法（下称改进Mehrotra型预估-校正算法）.这样，既能使迭代点始终在所讨论的宽邻域内，又能得到步长一个正的下界，进而证明了改进Mehrotra型预估-校正算法的迭代复杂性为O（n2log（x0）Ts0/ε）；通过对校正方向的稍加修改，他们将算法的迭代复杂性降至O（nlog（x0）Ts0/ε）（见文献［6］）.随后，Salahi等学者对线性规划的Mehrotra型预估-校正算法做了进一步研究.在文献［7］中，Salahi和Amiri基于文献［6］的思想，提出了一种求解线性规划的二阶Mehrotra型预估-校正算法（其要点是在原有的二阶Mehrotra型预估-校正算法中加“安全策略”），并证明了二阶算法与文献［6］的方法有相同的迭代复杂性.在文献［8］中，Salahi和Terlaky给出了线性规划的Mehrotra型预估-校正算法的一个新的改进形式.新方法的主要创新之处是在算法的校正步用“障碍参数的延时选择”（Postponing the choice of the barrier parameter）取代文献［6］中的“安全策略”，在精心给定一个校正步长的情况下，通过求解一个一维优化问题，得到目标障碍参数的取值范围，相应地可得到校正步搜索方向，最后证明了新算法与文献［6］的算法有相同的迭代复杂性.文章还得到了新算法的超线性收敛性，并给出了数值实验结果.最近，Salahi在文献［9］中提出了一种新的求解线性规划的Mehrotra型预估-校正算法，其主要创新之处是在算法的校正步利用自适应参数校正策略取代文献［6］中的“安全策略”，在没有采用任何安全策略的情况下，证明了新算法的迭代复杂性与文献［6］的迭代复杂性是一样的.前面几项改进工作，其基本想法都是设法使得Mehrotra型预估-校正算法“既保持迭代点在所讨论的宽邻域内，又能得到步长一个正的下界”.应该指出的是Salahi等人的改进Mehrotra型预估-校正算法文献［6-7］发表以后，人们通过利用Zhang［10］的对称化技术将其推广到半定规划［11-12］，并证明了算法的迭代复杂性.

基于文献［9］的思想，本文对半定规划提出了一个自适应校正参数Mehrotra型预估校正算法.收敛分析中遇到的主要困难是保持算法迭代方向的对称性.为此，采用Zhang［10］的对称化技术，通过建立和利用一些技术性引理，证明了算法的迭代复杂性为O（nlogX0·S0/ε），这与求解线性规划的相应算法有相同的迭代复杂性阶.

本文将用到如下符号：Rm表示m维欧式空间.Rn×n表示n×n实矩阵空间.Sn和Sn++分别表示n×n对称矩阵锥和对称正定矩阵锥.||·||F和||·||分别表示矩阵的Frobenius范数和谱范数.对任意M，N∈Sn，M≽N（或M≻N）表示M-N是半正定（或正定）矩阵，M·N=Tr（MTN）.对任意A∈Sn，λi（A）表示A的第i个特征值，λmin（A）和λmax（A）分别表示A的最小和最大特征值，cond（A）=λmax（A）/λmin（A）表示矩阵A的条件数.X⊗S表示矩阵X和S的Kronecker积.对任意X∈Rn×n，vec（X）表示矩阵的X的列展开.此外，I表示单位矩阵.

2　预备知识

本文讨论如下标准形式的半定规划：

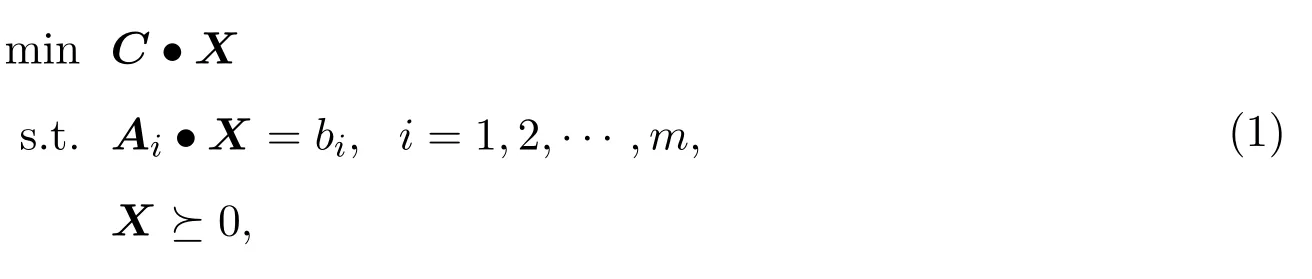
类似于文献［9］的引理2.2和2.4，可得以下两个引理.注意，在以下讨论中，取

由引理2.1和引理2.3可得到以下推论.

引理2.4对算法产生的所有迭代点（X，y，S），方程（11）总有两个正根.

综上，算法框架描述如下：

算法1

3　算法的复杂性分析

为简化主要结果证明，（9）式中第三式改写为以下等价式子：

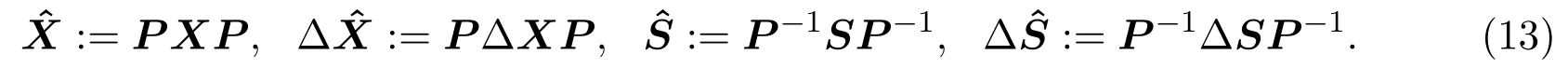
其中，H≡HI是普通对称化算子，由矩阵的Kronecker积、vec（·）的定义和（12）式，则有

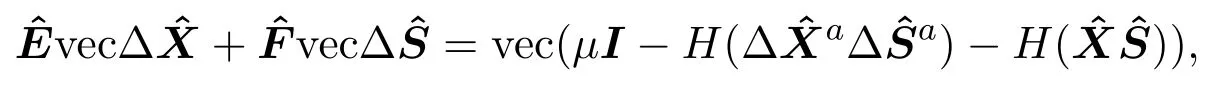
其中

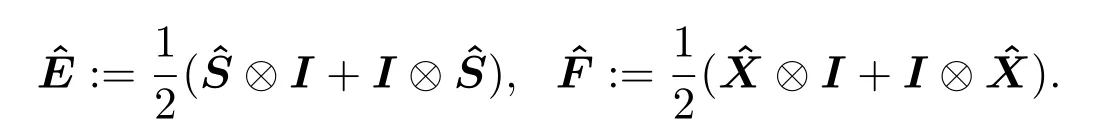
利用（7）式和（13）式有

为建立算法1的迭代复杂界，需确定校正步的最大步长αc的一个下界，下面几个引理起着重要作用.

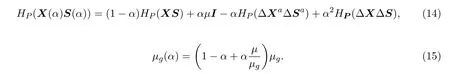
推论3.3假设P是N-T尺度矩阵，注意µ=µt，如果σ＞4且γ=1/σ，则有

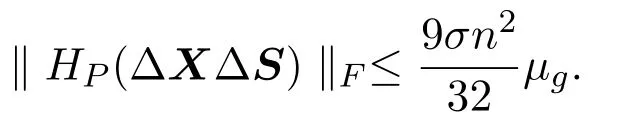
证明由引理2.2和引理3.2即可得证.

引理3.4假设P是N-T尺度矩阵，定义

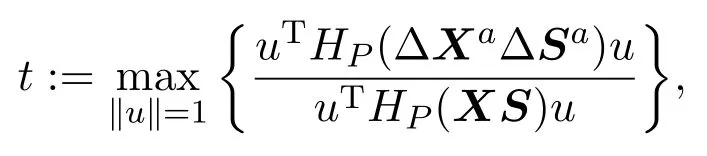
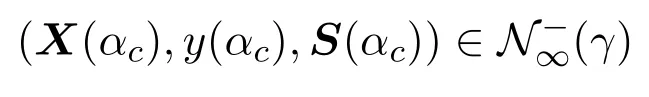
成立的最大步长αc满足

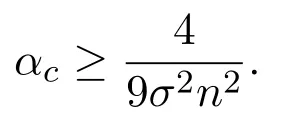
定理3.6算法1至多经过

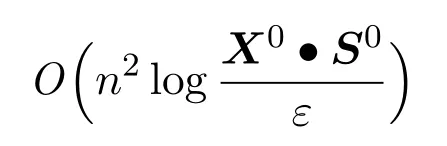
次迭代后，便可得到问题（1）和（2）满足X·S≤ε的ε-近似解.

4　数值结果

本节报告一些数值实验结果.设原始问题与对偶问题分别按（1）式与（2）式确定，其中

的情形［19］.下面在Matlab R2014 a环境下验证算法的可行性.容易验证X=I原始可行，y=（1，1，1）T和S=I对偶可行.取精度ε=10-7和不同的γ，对本文的算法1与文献［11］中的算法1（下称KT算法）进行测试，并对两者的测试结果进行比较（见表1）.从表1可知算法是可行的，迭代次数与γ有关，且γ相同时算法1先于KT算法终止迭代.又因为KT算法采取了安全策略，而我们的算法1没有采用任何的安全策略，所以本文提出的算法1与KT算法相比具有一定的优越性.

表1　本文算法1与KT算法的比较

［1］Karmarkar N K.A new polynomial-time algorithm for linear programming［J］.Combinatorica，1984，4：373-395.

［2］Mehrotra S.On the implementation of a primal-dual interior point method［J］.SIAM Journal on Optimization，1992，2：575-601.

［3］Andersen E D，Andersen K D.The Mosek Interior Point Optimizer for Linear Programming：an Implementation of the Homogeneous Algorithm［M］.Holland：Kluwer Academic Publishers，2000：197-232.

［4］Vanderbei R J.Loqo：an interior-point code for quadratic programming［J］.Optimization Methods and Software，1999，12：451-488.

［5］Zhang Y.Solving large-scale linear programmes by interior point methods under the Matlab environment［J］.Optimization Methods and Software，1999，10：1-31.

［6］Salahi M，Peng J，Terlaky T.On Mehrotra-type predictor-corrector algorithms［J］.SIAM Journal on Optimization，2007，18（4）：1377-1397.

［7］Salahi M，Mahdavi-Amiri N.Polynomial time second order Mehrotra-type predictor-corrector algorithms［J］.Applied Mathematics and Computation，2006，183：646-658.

［8］Salahi M，Terlaky T.Postponing the choice of the barrier parameter in Mehrotra-type predictor-corrector algorithms［J］.European Journal of Operational Research，2007，182：502-513.

［9］Salahi M.New Barrier Parameter Updating technique in mehrotra-type algorithm［J］.Bulletin of the Iranian Mathematical Society，2010，36（2）：99-108.

［10］Zhang Y.On extending some primal-dual interior-point algorithms from linear programming to semidefinite programming［J］.SIAM Journal on Optimization，1998，8：365-386.

［11］Koulaei H M，Terlaky T.On the extension of a mehrotra-type algorithm for semidefinite optization［R］.Hamilton，Ontario，Canada：McMaster University，2007.

［12］Zhang M W.A second order Mehrotra-type predictor-corrector algorithm for semidefinite optimization［J］.Journal of Systems Science Complexity，2012，25：1108-1121.

［13］Roos C，Terlaky T.Theory and Algorithms for Linear Optimization：an Interior Point Approach［M］.Chichester，UK：John Wiley and Sons，1997.

［14］Klerk De E.Aspects of Semidefinite Programming：Interior Point Algorithms and Selected Applications［M］.Dordrecht，The Netherlands：Kluwer Academic Publishers，2002.

［15］Nesterov Y E，Nemirovsky A S.Interior Point Methods in Convex Programming：Theory and Applications［M］.Philadelphia：Society for Industrial and Applied Mathematics，1994.

［16］Wolkowicz H，Saigal R，Vandenberghe L.Handbook of Semidefinite Programming，Theory，Algorithms，and Applications［M］.The Netherlands：Kluwer Academic Publishers，2000.

［17］Horn R A，Johnson C R.Matrix Analysis［M］.New York：Cambridge University Press，1990.

［18］Wright S J.Primal-Dual Interior-Point Methods［M］.USA：SIAM，1997.

［19］Wang G Q，Bai Y Q，Roos C.Primal-dual interior-point algorithms for semi-definite optimization based on a simple kernel function［J］.Journal of Mathematical Modelling and Algorithms，2005，4（4）：409-433.

A mehrotra-type algorithm for SDP based on a new adap-tive updating technique of barrier parameter

Huang Fangyan1，Zhang Mingwang1，Huang Zhengwei2
（1.College of Science，China Three Gorges University，Yichang 443002，China；2.College of Economics and Management，China Three Gorges University，Yichang 443002，China）

Salahi in his recent work proposed a Mehrotra-type predictor-corrector algorithm based on a new adaptive updating technique of barrier parameter for linear program，which enables him to derive the iteration complexity bound of Mehrotra-type algorithm without a safeguard.This paper extends the Mehrotra-type algorithm to semidefinite program.By using Zhang′s general symmetrization scheme，the polynomial iteration complexity bound of the algorithm is obtained，which is of the same order as that of the corresponding algorithm for linear program.

Mehrotra-type algorithm，semidefinite program，iteration complexity，symmetrization scheme

O178；O174.6

A

1008-5513（2015）06-0650-11

10.3969/j.issn.1008-5513.2015.06.014

2015-06-21.

国家自然科学基金（71471102）.

黄方艳（1990-），硕士生，研究方向：锥优化问题的内点算法.

张明望（1959-），硕士，教授，研究方向：最优化理论与应用.

2010 MSC：26D15，26D10