独立情形下自正则和的精确渐近性

付宗魁，吴群英

（桂林理工大学理学院，广西桂林541004）

独立情形下自正则和的精确渐近性

付宗魁，吴群英

（桂林理工大学理学院，广西桂林541004）

研究均值为零非退化的独立同分布的随机变量序列正则和收敛性，在适当条件下，获得了自正则和精确渐近性的一般结果.

独立同分布；自正则和；精确渐近性

1　引言及主要结果

随机变量序列的精确渐近性的研究是概率极限理论研究中的一个热门话题.近年来，得到了许多研究成果，文献［1-2］得到了独立情形下一阶矩收敛的精确渐近性；文献［3］得到了NA序列矩收敛的渐近性质.自正则极限理论的提出丰富了精确渐近性的理论研究，得到了一些自正则和的精确渐近性结果，文献［4］得到了自正则和矩收敛的精确渐近性.下面先介绍稳定吸引域的概念.

定义1.1称独立同分布的随机变量序列｛X，Xn，n≥1｝是属于稳定吸引域，如果存在An＞0和Bn∈R，使得

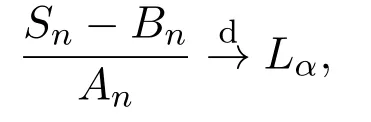
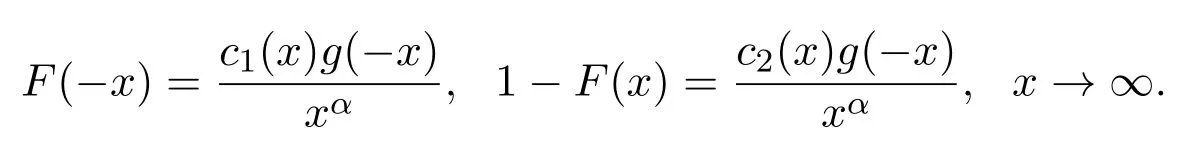
其中g（x）≥0为慢变化函数，ci（x）≥0，ci（x）→ci，x→∞，i=1，2，c1+c2＞0.

最近，文献［5］得到了独立同分布序列自正则和的一类完全矩收敛，即

本文在此基础上，研究了独立同分布情形下自正则和精确渐近性的一般结果.

在整篇文章中，

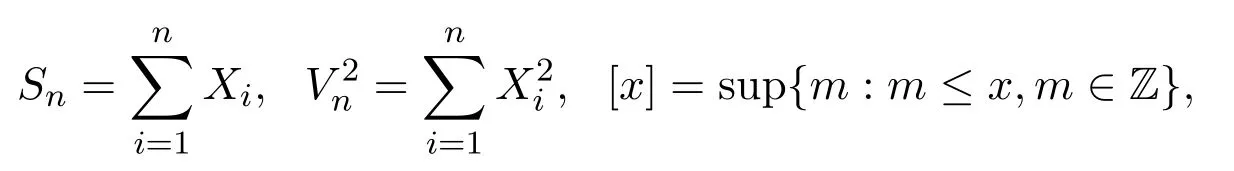
C在不同的位置表示不同的常数.下面先给出文中的一些假设条件.

定理1.2设｛X，Xn，n≥1｝是均值为0非退化的独立同分布的随机变量序列，且X属于正态吸引域，如果满足假设条件（i）、（ii）、（iii）和（v），则有

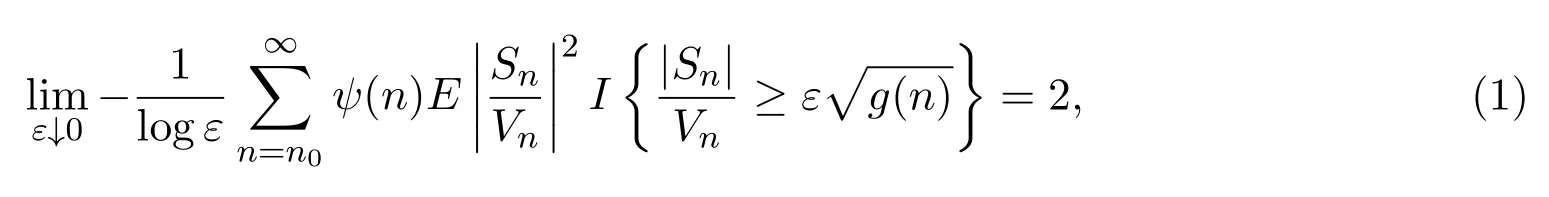
定理1.3设｛X，Xn，n≥1｝是均值为0非退化的独立同分布的随机变量序列，且X属于正态吸引域，如果满足假设条件（i）、（ii）、（iv）和（vi），则有

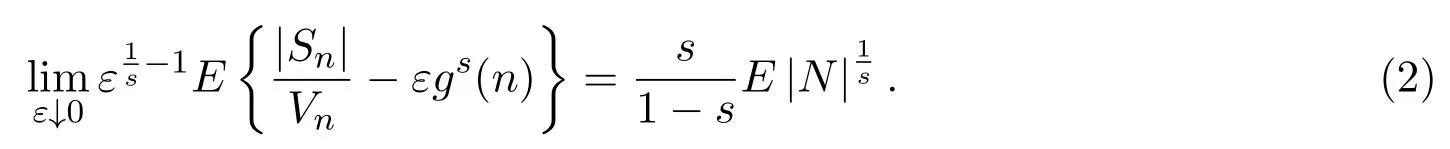
注1.1如果0＜σ2=EX2＜∞，由强大数定律知a.s.则以代替Vn，定理1.2和定理1.3仍成立.

注1.2满足假设条件中的g（x）有很多，比如g（x）=xα，（logx）β，（loglogx）γ.其中α＞0，β＞0，γ＞0为适当的参数.

2　引理

引理2.1［6］设｛X，Xn，n≥1｝是均值为0的独立同分布的随机变量序列，且X属于正态吸引域，则有

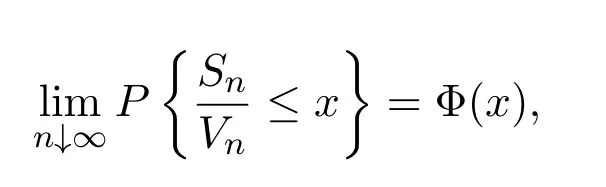
其中，Φ（x）为标准正态随机变量分布函数.

引理2.2［7］设｛X，Xn，n≥1｝是均值为0的独立同分布的随机变量序列，且X属于正态吸引域，如果满足假设条件（i）、（ii）和（v），则有

引理2.3［8］设｛X，Xn，n≥1｝是均值为0的独立同分布的随机变量序列，且X属于正态吸引域，则对于任意的存在0＜δ＜1，x0＞1，N0，使得当n≥N0和时，有

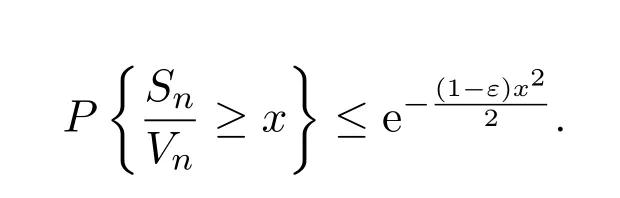
引理2.4［1］设｛ani，1≤i≤n，n≥1｝为实数阵列，｛Xi，i≥1｝为实数序列且满足条件：对任意的i≥1，ani→0，n→∞.对任意的

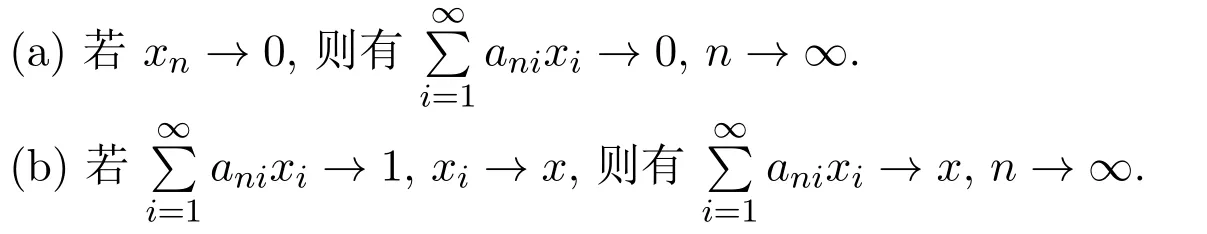
3　定理1.2的证明

性质3.1在定理1.2的条件下，有

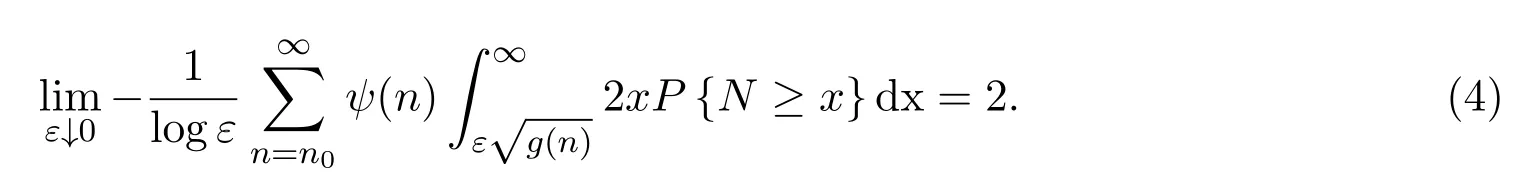
证明参见文献［9］的性质4.1.

性质3.2在定理1.2的条件下，有

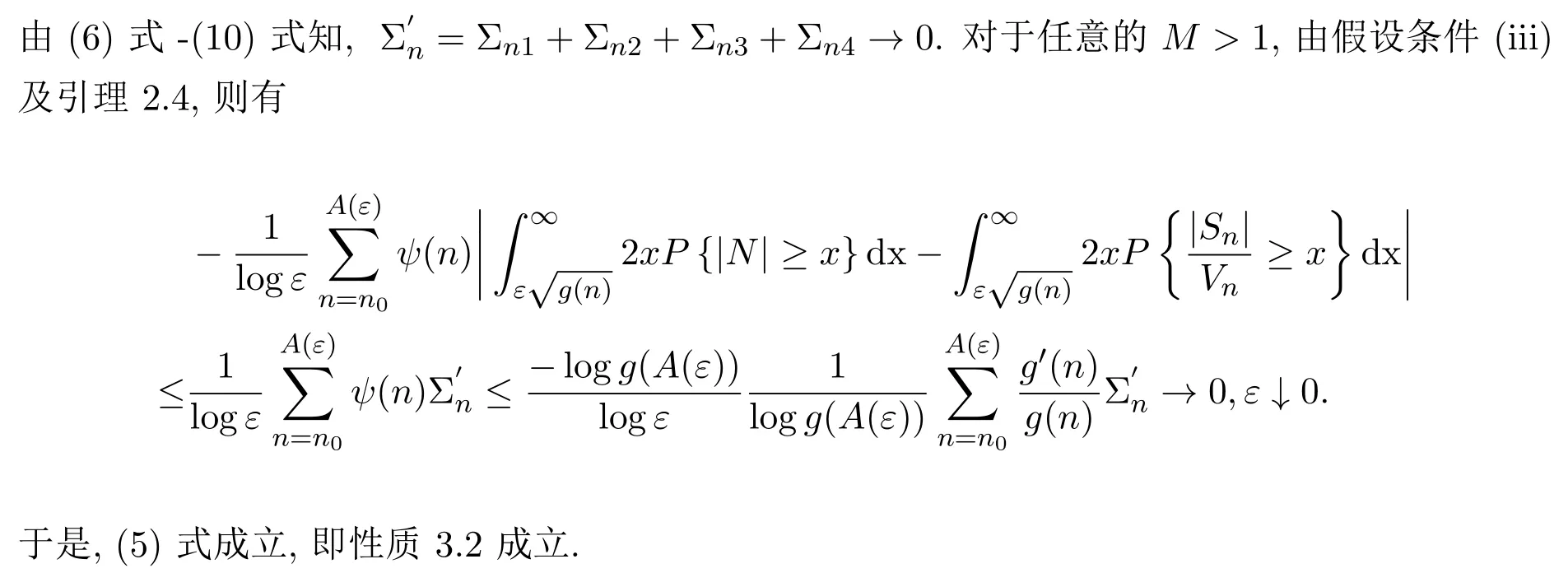
性质3.3M＞4设在定理1.2的条件下，有

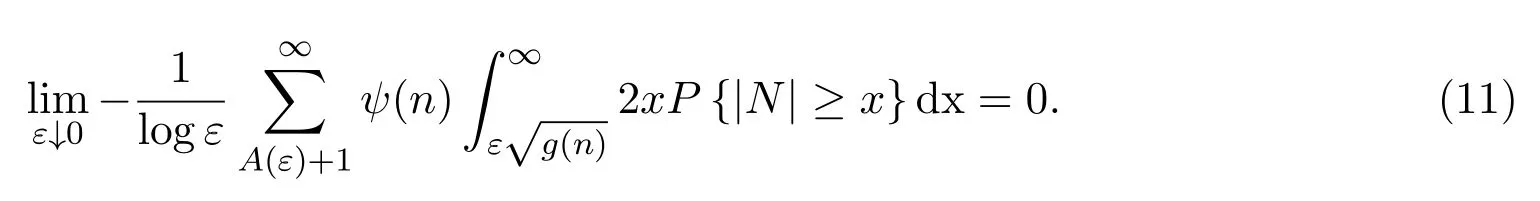
证明参见文献［9］的性质4.3.

性质3.4在定理1.2的条件下，有

定理1.2的证明由性质3.1-性质3.4及三角不等式可知（3）式成立，即定理1成立.

4　定理1.3的证明

由文献［7］的定理1.1的（1.2）式知（13）式成立，即定理1.3成立.

［1］Hall P，Heyde C C.Martingale Limit Theory and Its Applications［M］.New York：Academic Press，1980.

［2］孙晓祥，杨丽娟.独立情形下一阶矩收敛的精确渐近性的注记［J］.吉林大学学报，2013，51（5）：871-875.

［3］Zhao Y X.Asymptotic properties of the moment convergence for NA sequences［J］.Acta Mathematica Scientia，2014，34B（2）：301-312.

［4］Zhao Y X，Tao J X.Precise asymptotics in complete moment convergence for self-normalized sums［J］.Computers and Mathematics with Applications，2008，56：1779-1786.

［5］Zang Q P.A kind of complete moment convergence for self-normalized sums［J］.Computers and Mathematics with Applications，2010，60：1803-1809.

［6］Gine E，Gotze F，Masson D M.When is the student t-statistic asymptotically standard normal［J］.Ann.Probab，1997，25：1514-1531.

［7］陆振刚，姜玉秋.自正则部分和精确渐近性的一般结果［J］.华东师范大学学报，2013（2）：146-153.

［8］Griffin P S，Kuelbs J.Some extensions of the LIL via self-normalized sums［J］.Ann.Probab.，1991，19：380-395.

［9］Zhang Y，Yang X Y，Dong Z S.A general law of precise asymptotics for the complete moment convergence［J］.Chin.Ann.Math.，2009，30B（1）：77-90.

［10］Zang Q P.A general law of complate moment convergence for self-normalized sums［J］.Inequalities and Applications，2010，46（1）：155-161.

Precise asymptotics for self-normalized sums of independent and identically distributed random variables

Fu Zongkui，Wu Qunying

（College of Science，Guilin University of Technology，Guilin 541004，China）

This paper study the convergence of normalized sums for independent and identically distributed nondegenerate random variables with mean zeros，under some conditions，we obtain a general result on precise asymptotics for self-normalized sums.

independent and identically distributed，self-normalized sums，precise asymptotic

O211.4

A

1008-5513（2015）06-0596-08

10.3969/j.issn.1008-5513.2015.06.007

2015-05-04.

国家自然科学基金（11361019）；广西自然科学基金（2013GXNSFDA019001）；广西高校人才小高地建设创新团队资助计划（桂教人［2011］47号）.

付宗魁（1990-），硕士生，研究方向：概率论与数理统计.

2010 MSC：60F15