可压缩向列型液晶自由边界问题整体弱解的内正则性

黄金锐，陈宗妍，钟康梅



可压缩向列型液晶自由边界问题整体弱解的内正则性

黄金锐，陈宗妍，钟康梅

（五邑大学 数学与计算科学学院，广东 江门 529020）

讨论了一维可压缩向列型液晶系统的自由边界问题在初始真空连续连接的条件下整体弱解的内正则性.

可压缩向列型液晶；自由边界；弱解；内正则性

1 问题简述

本文考虑一维可压缩向列型液晶系统[1-3]：

系统满足初始值：

以及下列边界条件：

对上述系统考虑拉格朗日变换 ：，，变换后可得：

此时系统满足初始值：

以及边界条件：

引理1[3]1656假设初始值满足下列条件：

式（4～6）存在整体弱解，满足下列正则性：

2 本文的主要结果及其证明

由经典的估计方法[2]可得密度函数的正下界和上界估计，即如下引理.

证明 由式（4）1可得：

式（4）2等式两端在上积分，可得：

.

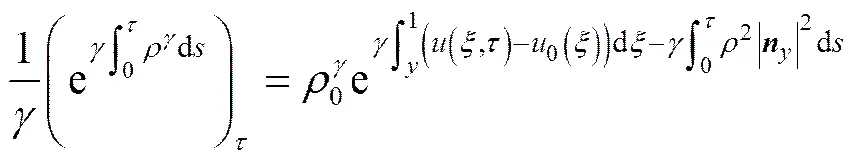
因此有：

根据系统的基本能量等式，我们有：

从而有：

根据上述估计以及式（8），可得式（9）. 另外，根据文献[3]的推导还能得到如下引理.

引理3[3]1658~1671关于问题（4～6）的弱解有如下先验估计：

下文将运用引理2以及引理3的结论推导本文的主要结果. 由引理2可知，密度函数具有正下界和上界估计，从而根据式（17）有：

另外，

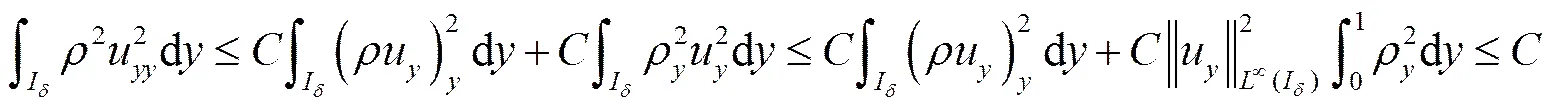
因此，我们有：

，

再根据Cauchy不等式以及先前的能量估计，可得：

根据式（4），可得本文主要结论如下.

注：由于缺乏密度函数的空间方向二阶导数的有效估计，因此无法得到、以及的估计.

[1]丁时进. 液晶模型的分析理论[J]. 华南师范大学学报（自然科学版），2013, 45(3): 1-7.

[2] DING Shijin, HUANG Jinrui, XIA Fengguang. A free boundary problem for compressible hydrodynamic flow of liquid crystals in one dimension [J]. J Differential Equations, 2013, 255: 3848-3879.

[3] HUANG Jinrui, DING Shijin. Compressible hydrodynamic flow of nematic liquid crystals with vacuum [J]. J Differential Equations, 2015, 258: 1653-1684.

[责任编辑：熊玉涛]

Interior Regularity of Global Weak Solutions to One-dimensional Free Boundary Problem for Compressible Nematic Liquid Crystals

HUANGJin-rui, CHEN Zong-yan, ZHONGKang-mei

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

This paper deals with the interior regularity of global weak solutions to free boundary problems of the one-dimensional compressible nematic liquid crystal system which connects continuously to vacuum.

compressible nematic liquid crystal; free boundary; weak solution; interior regularity

1006-7302（2015）04-0001-04

O175.25；O175.26

A

2015-01-12

国家自然科学基金资助项目（11401439）；广东省普通高校青年创新人才项目（2014KQCX162）；五邑大学青年基金资助项目（2014zk06）；广东省大学生创新创业训练计划项目（201511349089）

黄金锐（1984—），男，广东佛山人，讲师，博士，主要从事偏微分方程的理论研究.

①此处修正了文献[3]中的一处笔误.