复双曲离散理想三角群

黄小琳，曹文胜



复双曲离散理想三角群

黄小琳，曹文胜

（五邑大学 数学与计算科学学院，广东 江门 529020）

复双曲三角群是由3条复测地线上的复反射生成的，本文主要讨论复双曲理想三角群的离散性. 通过复测地线相对应的极向量定义了角度参数，该角度不变量可以决定一个三角群，并由该角度不变量给出了复双曲空间中理想三角群离散的必要条件.

复双曲空间；理想三角群；离散嵌入；角度不变量

我们定义复双曲三角群是由复测地线上的复反射生成的指数为2的群，是的一个子群[8]. 用表示一条复测地线, 定义一个复双曲三角群为一个三元组：若两条复测地线和相交于点，夹角为，则可以用三元组来表示三角群. 令表示一个抽象的复三角群：

.

本文主要研究复双曲理想三角群离散的必要条件. 文献[4]通过3个边界点确定了一个cartan角度不变量，利用迹的判断条件给出了复双曲理想三角群离散的必要条件. 本文拟通过复测地线上的极向量确定一个角度不变量，再利用文献[9]中给出的等距映射分类的判断方法得到复双曲理想三角群离散的必要条件.

1 预备知识

关于复双曲空间的相关知识，可以参考文献[10-11]. 复数的共轭元素，并且记的模为. 定义和分别为的实部和虚部. 若2个复数和相似，用表示，则存在一个非零复数使得.

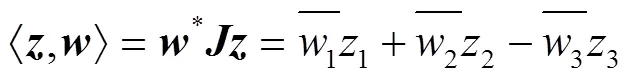
根据文献[10]，令

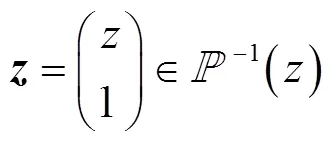
利用Hermitian叉乘运算，可得到极向量

根据文献[13]，我们可以定义复双曲空间中的反射映射. 给定一条复测地线，若在中存在唯一一个等距变换以复测地线为不动点，则称为复测地线的复反射. 这个复反射可以表示为：

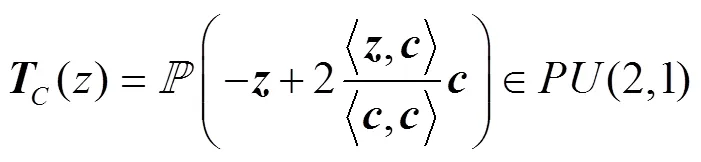
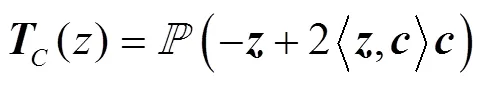
下面将对这3种情况进行细分：

Cao和Gongopadhyay 在文献[9]中给出一个判断元素类型的代数方法：记，则任意的可表示为，其中. 作到的一个嵌入：，其中，于是有如下引理.

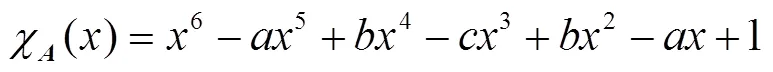
3 主要结论

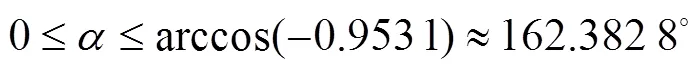
经计算，有

根据引理1得：

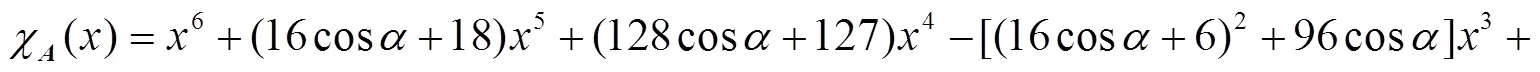
经计算得：

.

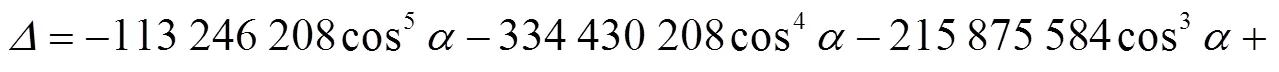
4 总结和推广

在证明本文的主要结论时，通过式（3）我们得到了所取3个点的角度不变量，这不同于cartan角度不变量. 由于迹在的作用下是变化的，故运用迹来判断元素类型的方法在四元数双曲空间是行不通的. 文献[9]给出的判断元素类型的方法在复双曲空间和四元数双曲空间都适用，所以本文采用了文献[9]的判别方法. 下一步希望可以将主要结论推广到四元数双曲空间.

[1] CHEN Shengshen, GREENBERG L. Hyperbolic spaces [M]//Contributions to Analysis a Collection of Papers Dedicated to Lipman Bers. New York: Academic Press, 1974: 49-87.

[2] BEARDON A F. The geometry of discrete groups [M]. Berlin, New York: Spring-Verlag, 1983.

[3] PARKER J R. Complex hyperbolic lattices [M]//Contemp Math, USA: American Mathematical Society, 2009:1-42.

[4] GOLDMAN W M, PARKER J R. Complex hyperbolic ideal triangle groups [J]. J Reine Agnew Math, 1992, 425: 71-86.

[5] SCHWARTZ R E. Ideal triangle groups, dented tori, and numerical analysis [J]. Annals of Math, 2001, 153: 533-598.

[6] SCHWARTZ R E. Complex hyperbolic triangle groups [J]. Differential Geometry, 2003, 5: 339-349.

[7] SCHWARTZ R E. A better proof of the Goldman-Parker conjecture [J]. Geom Topol, 2005, 9: 1539-1601.

[8] WYSS-GALLIFENT J O. Complex hyperbolic triangle groups [D]. Maryland: University of Maryland, 2000.

[9] CAO Wensheng, GONGOPADHYAY K. Algebraic characterization of isometries of the complex and the quaternionic hyperbolic planes [J]. Geometriae Dedicata, 2012, 157: 23-39.

[10] PARKER J R. Notes on complex hyperbolic geometry [M]. Preliminary Version. Cambridge: Cambridge University Press, 2003.

[11] GOLDMAN W M. Complex hyperbolic geometry [M]. Oxford: Oxford University Press, 1999.

[12] THOMPSON J M. Complex hyperbolic triangle groups [D]. Durham: Durham University, 2010.

[13]PRATOUSSEVITCH A. Traces in complex hyperbolic triangle groups [J]. Geometriae Dedicat, 2005, 111: 159-185.

[责任编辑：熊玉涛]

The Discreteness of Complex Hyperbolic Ideal Triangle Groups

HUANGXiao-lin, CAOWen-sheng

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

Complex hyperbolic triangle groups are generated by three complex reflections of complex geodesics. This paper discusses the discreteness of complex hyperbolic ideal triangle groups. Using the polar vector of a complex geodesic, we construct an angular invariant. Such groups are parameterized by a real invariantof triangles in the complex hyperbolic space. Furthermore, this angular invariant can uniquely determine a-triangle. Using the angular invariant, we obtain a necessary condition for a discrete embedding of a complex hyperbolic ideal triangle group.

complex hyperbolic spaces; ideal triangle groups; discrete embedding; angular invariants

1006-7302（2015）04-0010-06

O151.21

A

2015-06-30

广东省自然科学基金资助项目（2015A030313644）

黄小琳（1990—），女，广东潮州人，在读硕士生，研究方向为复分析；曹文胜，教授，博士，硕士生导师，通信作者，研究方向为复分析.