定周期单路口绿信比的迭代学习控制方法

周昊，阮太元，刘智勇,



定周期单路口绿信比的迭代学习控制方法

周昊1，阮太元2，刘智勇1,2

（1.五邑大学 信息工程学院，广东 江门 529020；2.江门职业技术学院，广东 江门 529020)

为减少公路路口车辆的延误时间，提高交通干线的通行效率，本文利用迭代学习控制方法改善信号控制的效果. 在设定初始交通参数后，以车辆排队长度为状态变量，以绿信比为控制学习律，经过迭代学习控制得到实际车辆排队长度和理想车辆排队长度的误差，再利用控制学习律对误差进行多次修正，使绿信比趋向于理想值. MATLAB仿真实验表明：在不同的交通负载情况下，迭代学习控制算法对交通信号绿信比的优化确实有明显的效果.

干线协调控制；绿信比；迭代学习控制；排队长度

在城市交通网络中，交通干线通常承担着巨大的交通负荷，实施交通干线的协调控制对改善城市区域交通状况往往具有很明显的效果[1]. 交通信号控制遇到的最大困难在于交通需求的变化是随机的和动态的，如偶发性交通拥挤事件或事故引起的交通流突变、由驾驶者的人为因素导致的交通需求不规则增减等，其动特性的结构和参数导致无法建立传统的解析数学模型. 但交通管理者又要求控制系统必须具有较强壮的在线自适应性，也就是说系统能够在线优化配时方案并进行有效的实时控制[2]. 因此，当周期和相位差确定后，就需要对路口的绿信比进行优化.

线控干道每个路口的信号控制通常分为一天若干个时段（通常不超过20个），每一个时段内周期长度是不变的，必须通过调整各个相位的绿时来响应交通流的变化，从而最大限度地减少排队长度. 显然，每一个时段可把单个路口看作是一个重复运行（按照确定的周期）的受信号控制的对象. 为此，本文采用迭代学习控制方法来改善信号控制的效果. 迭代学习控制方法是一种在线控制方法，当控制器重复完成某一项控制任务时，可以从过去的控制输入和跟踪误差数据中获得额外的信息，这种信息可以看作是一种经验知识，在没有精确的过程模型的情况下，利用这样的经验知识去选择合适的学习律，可以保证算法的收敛性和学习速度，使得信号控制及时跟踪各相位交通流的变化，最大限度地减少车辆排队长度. 本文采用开环的迭代学习控制，以绿信比作为开环控制的控制变量，采用P型学习律. 为了保证迭代学习的收敛性，这里采用谱半径的方式，设定学习增益参数，保证了迭代学习的收敛性和效率. 最后用MATLAB仿真软件模拟迭代学习控制对绿信比的优化效率的影响.

1 迭代学习控制算法基本原理

输出误差为

离散时间系统下第次迭代运行可表示为：

在迭代学习控制研究中，一般假定系统满足如下假设条件[6]：

2）系统的期望轨迹是预先给定的；

4）系统为固定结构，即系统的函数关系在控制过程中不变；

2 干线协调控制下基于迭代学习控制算法的单路口信号绿信比优化

2.1 交通模型

在干线协调控制的战术层面，周期和相位差已经确定，优化干道上每个路口绿信比是解决问题的关键. 在实际交通干线协调控制实践中，各路口所遵循的相同信号周期一般不能频繁变化，以免引起交通紊流，进而造成交通混乱. 这意味着干道上每个路口的信号是按时段运行的.

定义

输出方程为：

式（8）和式（9）就构成了典型的线性定常离散系统的状态方程和输出方程. 很显然，当实际交通流量不超过路口的设计通行能力时，其理想的灯控路口的排队长度应为0. 然而，交通干线协调控制内各路口的交通需求是不平衡的，因此车辆排队现象有时是不可避免的.

根据以上描述，我们构造这样一种运行过程：在一个时段内，其周期是不变的，每（）个周期为一次运行迭代，重写式（8）和（9）：

于是迭代学习的控制律可以写成：

2.2 算法基本描述

算法步骤如下：

1）初始化各项基本交通数据，其中初始绿时大于最小绿时.

5）重复步骤2）、3）、4），直到完成设定的迭代次数.

3 仿真结果

使用MATLAB仿真软件模拟干线协调控制下单路口绿信比优化采用迭代学习控制算法的迭代效果，分别在低车流密度、高车流密度、以及从低车流密度到高车流密度或者从高车流密度到低车流密度过渡的情况下，分析迭代学习控制对绿信比的优化效率. 其中主要交通参数设置同上，车辆密度分别采用符合泊松分布的随机数模拟低车流密度、符合二项分布的随机数模拟高车流密度、符合负二项分布的随机数模拟过渡状态的车流密度[5]，并将每一个时段划分为60个周期选择60个随机数摸拟不同车流密度情况下的车辆到达率，同时输出每次迭代后车辆的排队长度变化情况以及误差曲线，即理想值和实际输出值之间的差值.

低车流密度情况下，采用迭代学习控制算法的仿真效率如图2至图4所示.

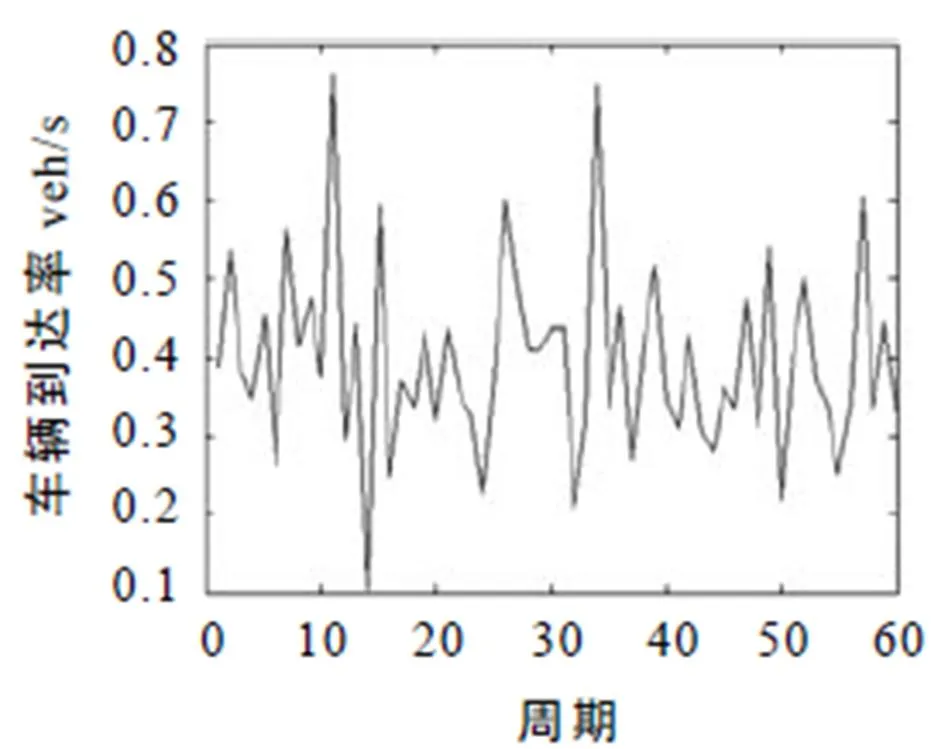
图2 低密度车流随机数分布

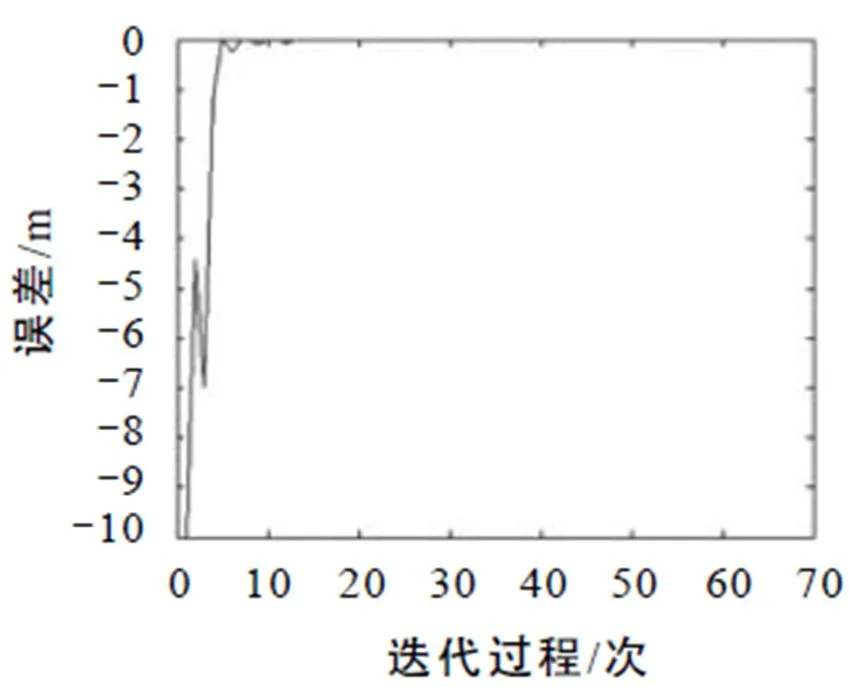
图4 低密度车流的迭代误差曲线

图2至图4反映在低车流密度时迭代学习控制算法对绿信比的优化效率. 对于较低的车流密度，迭代学习控制算法经过若干次调节后使车辆的排队长度逐渐减小，直至排队长度减少为0. 由于理想排队长度为0，因此图4的误差曲线和图3的车辆排队长度曲线相反.

高车流密度情况下，采用迭代学习控制算法的仿真效率如图5至图7所示.

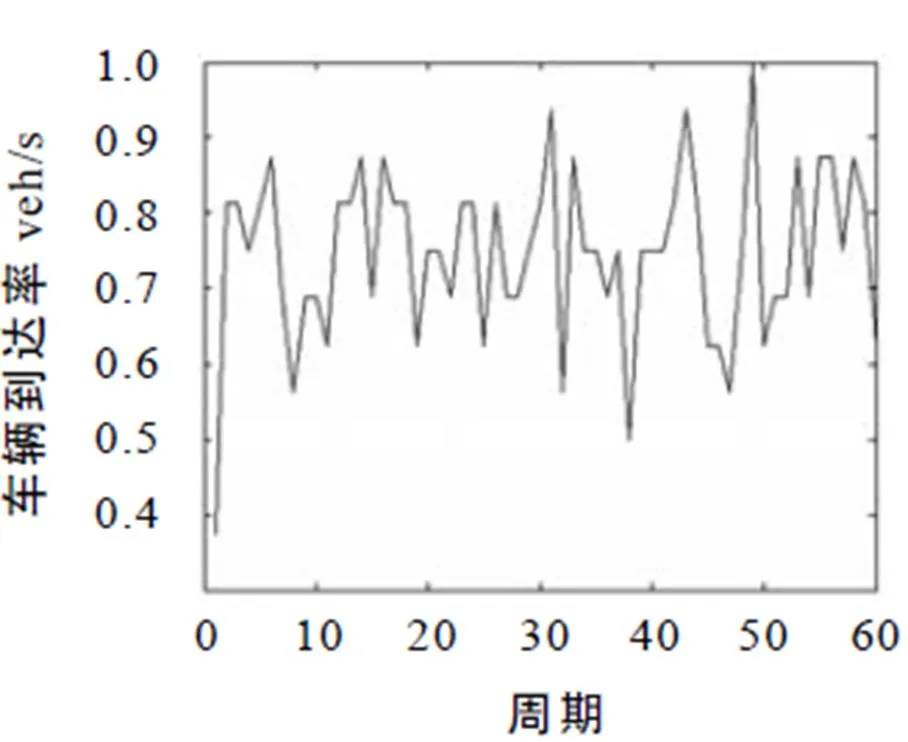
图5 高密度车流随机数分布

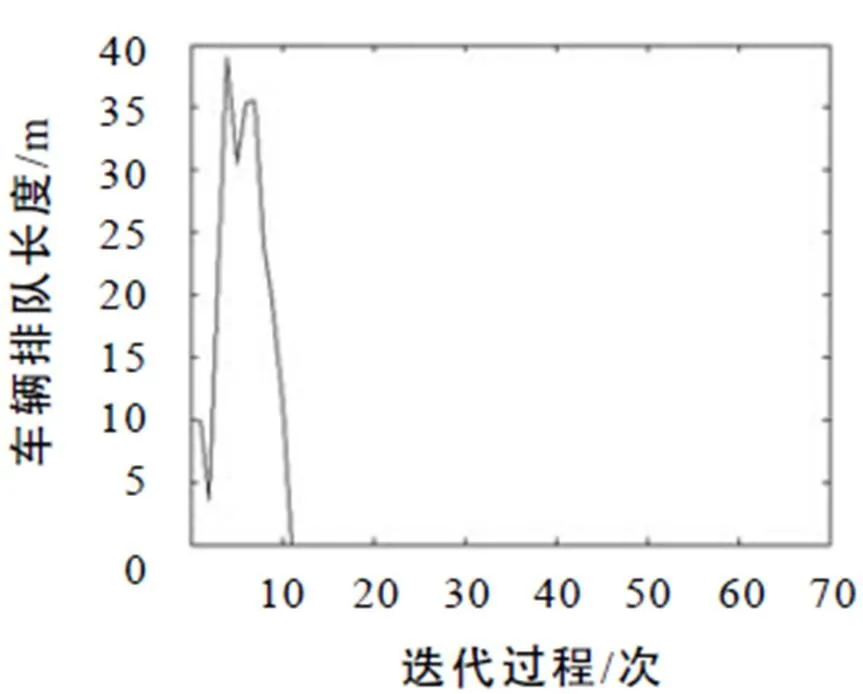
图6 高密度车流下车辆排队情况

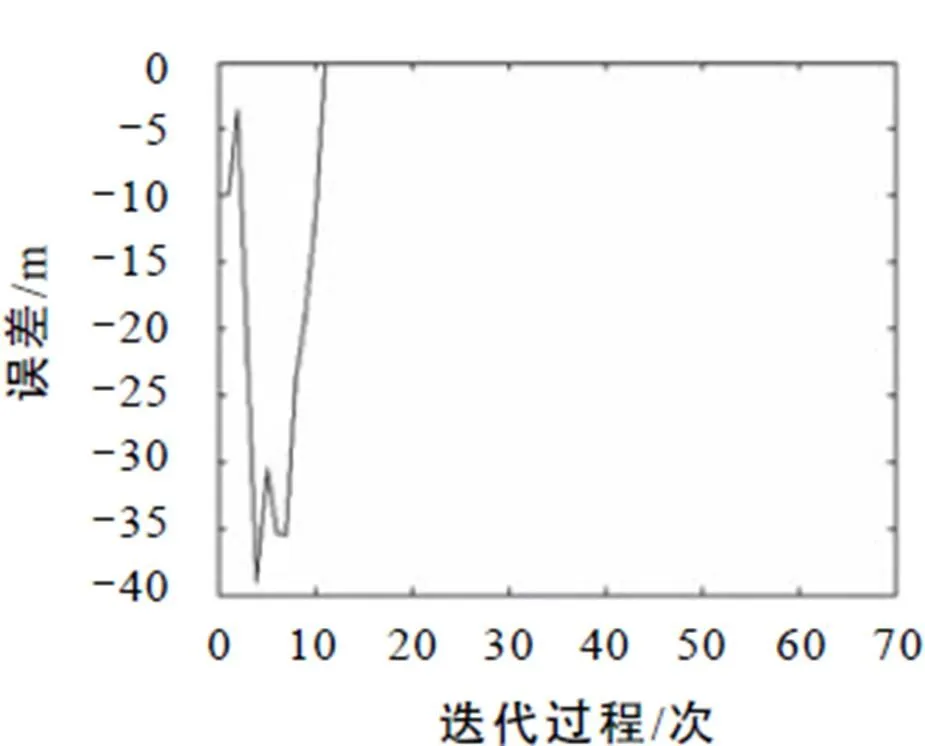
图7 高密度车流的迭代误差曲线

图5至图7反映在高车流密度时迭代学习控制算法对绿信比的优化效率. 由于车流密度较大，初期的车辆排队长度较大，但是经过若干次迭代学习算法调节后，车辆的排队长度呈现减小趋势，直至排队长度为0. 图7的误差曲线和图6的趋势相反，且经过若干次的迭代之后，误差趋于0.

方差较大的过渡车流密度情况下，采用迭代学习控制算法的仿真效率如图8至图10所示.

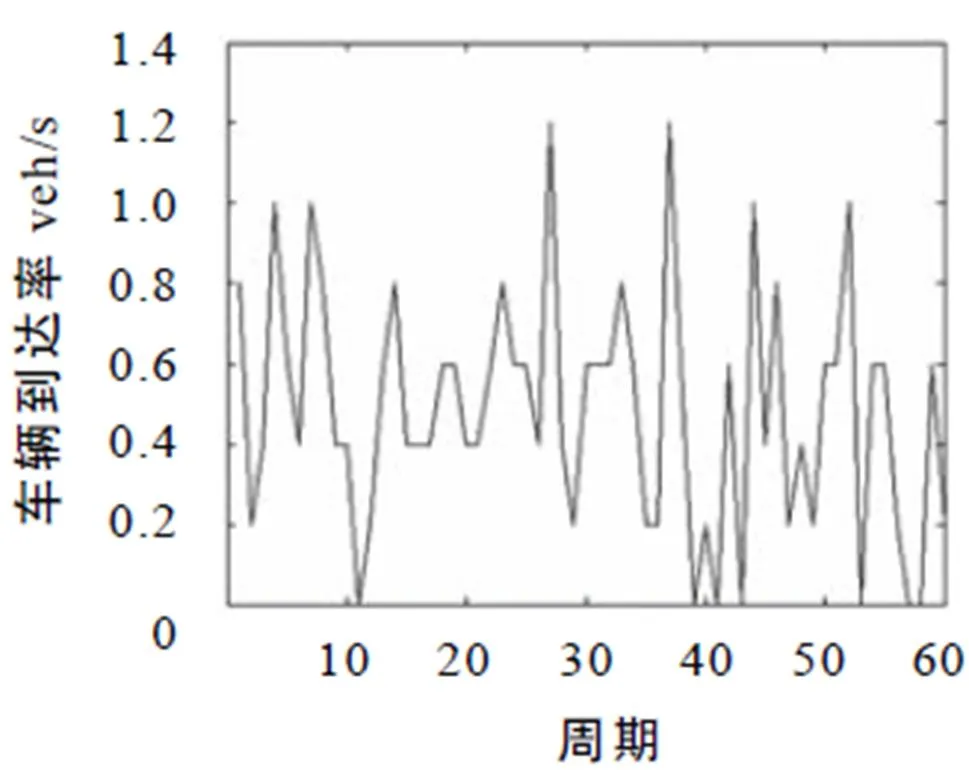
图8 过渡密度车流随机数分布

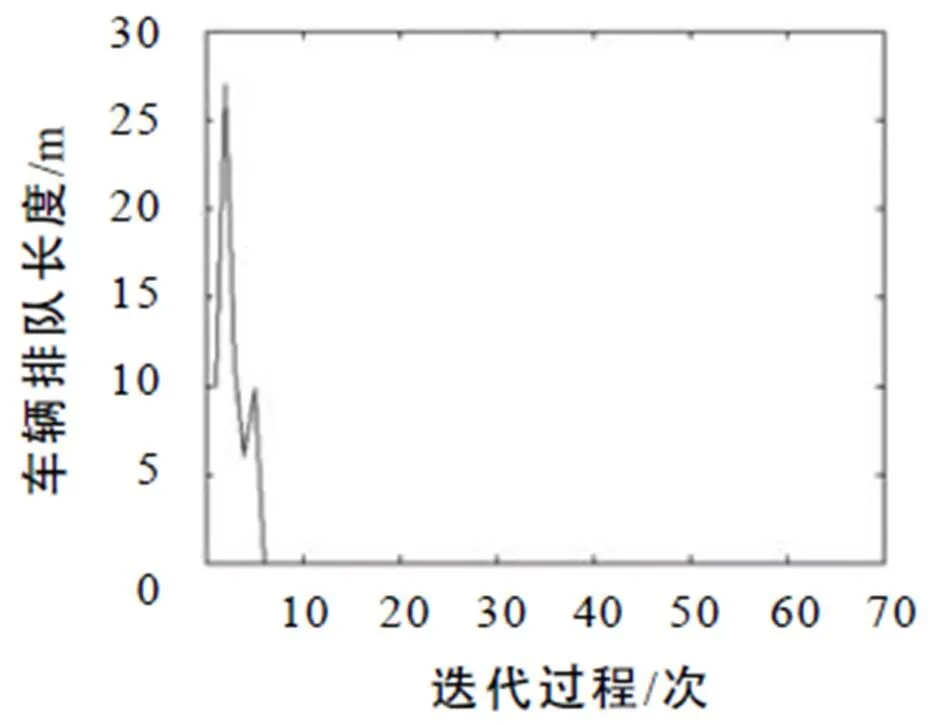
图9 过渡密度车流下车辆排队情况

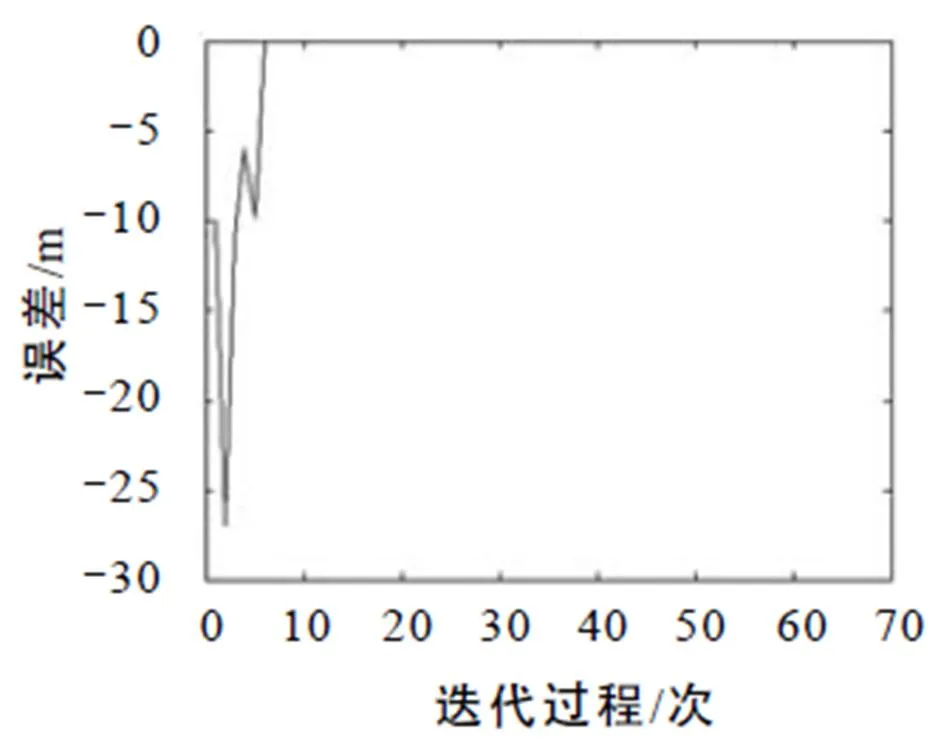
图10 过渡密度车流的迭代误差曲线

图8至图10反映在过渡车流密度时迭代学习控制算法对绿信比的优化效率. 由于车流密度波动较大，车辆的排队长度也随之出现波动，但从图9的车辆排队长度曲线和图10的误差曲线可以看出，经过若干次迭代后，车辆的排队长度呈现减小的趋势，直至趋于0.

4 结论

通过上述仿真结果可以得出结论：在干线协调控制下，确定了周期以及相位差后，采用迭代学习控制算法对单路口交通信号绿信比进行优化效果比较明显，反映采用迭代学习控制算法使单路口车辆延误时间得到一定的改善，而且单个路口通行效率的提高，对于整个干线通行效率提高也会有较大的帮助.

[1] 刘智勇. 智能交通控制理论及其应用[M]. 北京：科学出版社，2003.

[2] 郑一辰，张毅，胡坚明. 一种基于迭代学习的自适应交通信号控制方法[J]. 交通运输系统工程与信息，2010，12(6):34-40.

[3] 于少娟，齐向东，吴聚华. 迭代学习控制理论及应用[M]. 北京：机械工业出版社，2005.

[4] 谢胜利，田森平，谢振东. 迭代学习控制的理论和应用[M]. 北京：科学出版社，2005.

[5] 王殿海. 交通流理论[M]. 北京：人民交通出版社，2007.

[6] 陈定喜. 迭代学习控制算法研究[D]. 广州：华南理工大学，2010.

[7] BRISTOW D, THARAYIL M, ALLEYNE A G. A survey of iterative learning control [J]. Control System, 2006, 26(3): 96-114.

[8] 林辉，戴冠中. 迭代学习控制理论进展和挑战[J]. 控制理论与应用，1994, 11(2): 250-255.

[责任编辑：韦 韬]

An Iterative Learning Control Arithmetic for Signal Intersection’s Split

ZHOUHao1, RUANTai-yuan2, LIUZhi-yong1,2

(1. School of Information Engineering, Wuyi University, Jiangmen 529020, China;2. Jiangmen Ploytechnic College, Jiangmen 529020, China)

In order to reduce the delay time and improve traffic efficiency, this paper adopts the iterative learning control method to improve the effect of signal control. After the initial traffic parameters are set, the vehicle queue length is set as a status variable and split as the learning control law, the error of the actual queue length to the ideal queue length is obtained by iterative learning control, the error is then corrected multiple times by means of control learning law and the split is near the ideal. MATLAB simulation experiments show that: in different traffic load situations, the iterative learning control algorithm has obvious effect on the optimization of traffic signal split.

trunk coordination control; split; iterative learning control; queue length

1006-7302（2015）04-0057-05

U121

A

2015-03-24

周昊（1990—），男，安徽滁州人，在读硕士生，研究方向为智能交通控制；刘智勇，教授，博士，硕士生导师，通信作者，研究方向为模式识别与智能系统.