角动量的理论研究

尹芬芬

（铜仁学院 物理与电子工程学院，贵州 铜仁 554300 ）

角动量的理论研究

尹芬芬

（铜仁学院 物理与电子工程学院，贵州 铜仁 554300 ）

研究一些物理问题时，我们会遇到质点或质点系相对于参考点或绕轴转动的情况，此时用速度、动量都不能解决，因此物理学中引入了新的物理量—角动量。角动量能准确地描述物体的转动状况，在量子领域中也能反映表征状态，并且在现代技术中有着广泛的应用。本文从角动量的定义出发，对质点对参考点、质点绕定轴、质点系绕定轴等不同情况下的角动量定理及守恒定律进行了研究，并对动量守恒和角动量守恒的区别与联系以及角动量的知识应用等进行了探讨。

角动量；质点；转动

1.引言

角动量是大学物理中的重要参量，它能准确地描述物体的转动情况。它在经典物理、航空技术、近代物理理论中都扮演着极其重要的角色，是物理学中重要的力学概念之一［1］。下面我们具体研究各种情况下物体角动量及其相关定理和定律。

2.各种情况下角动量定理及守恒定律

2.1.质点对参考点的角动量研究

2.1.1.质点对参考点的角动量

如图所示，该质点质量为m，速度为v→，其相对于参考点O的位矢为r→，那么该质点对O点而言，其角动量定义为：的大小为L=rmvsinφ，其中φ为和→的夹角。→垂直于→和→所在平面，指向满足右手螺旋定则。

由于速度及位矢都是矢量，在直角坐标系中可

分别表示成：

可得质点相对于参考点的具体表达式：

2.1.2.质点对参考点的角动量定理

需要说明的是：力矩、角动量均对惯性系的同一参考点而言，且该点为定点时，才满足上式。

2.1.3.质点对参考点的角动量守恒定→律

2.2.质点对固定轴（设为z轴）的角动量

2.2.1.质点对固定轴的角动量

设某一质点绕z轴转动，那么质点对z轴的角动量为它对轴上任意点的角动量沿该轴的分量。可得质点对z轴的角动量为

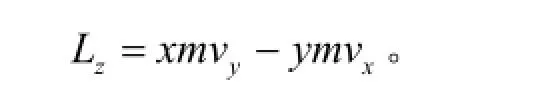
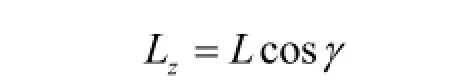
2.2.2.质点对固定轴的角动量定理

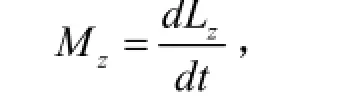
式中zM 是对z轴的力矩，zM 的具体求法：对该轴线上某点的力矩M在该轴线上的投影。

2.2.3.质点对固定轴的角动量守恒定律

2.3.质点系对参考点的角动量研究

2.3.1.质点系对参考点的角动量［3］

质点系是由许多个质点组成的系统，比如刚体就是特殊的质点系，它可看做由很多质点组成，且各质点间的距离保持不变。质点系对定点的角动量的定义为各质点对该点的角动量的矢量和。

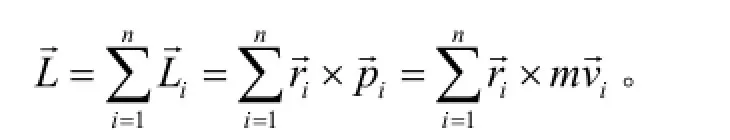
2.3.2.质点系对参考点的角动量定理

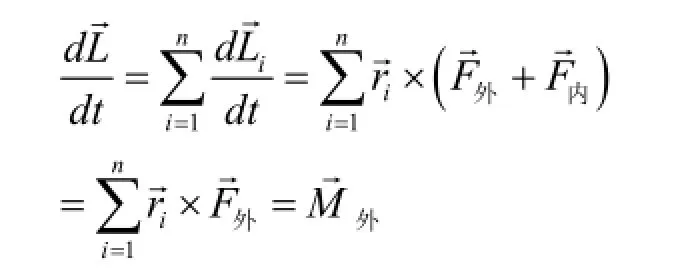
因为质点系之间的力总是成对出现，且大小相等，方向相反，所以内力矩之和M内=0。

2.3.3.质点系对参考点的角动量守恒定律

当M外=0，那么质点对该点的角动量守恒，即=常矢量。质点对固定轴角动量守恒包括三种情况：（1）=0；（2）质点系所受的外力均通过该参考点；（3）单个外力的力矩不为 0，但总外力矩M外=0

2.4.质点系对定轴z轴的角动量

我们研究特殊的质点系—质量分布均匀的刚体绕固定对称轴z轴的转动情况。

2.4.1.刚体对定轴的角动量

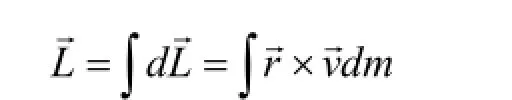
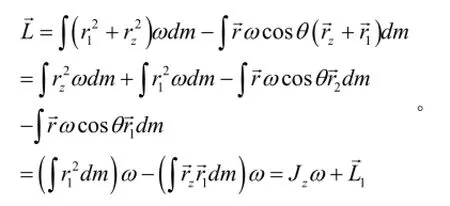
由此可知，只有固定轴z轴是质量均匀分布的刚体对称轴，即 Z轴为刚体的主转动惯量时［4］，才满足：

2.4.2.质点系对定轴的角动量定理

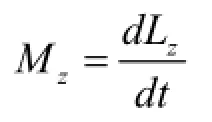
当固定轴z轴是质量均匀分布的刚体对称轴时，有：

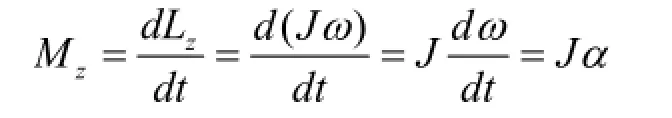
2.4.3.质点系对定轴的角动量守恒定律

2.5.刚体进动时的角动量

所谓进动指物体在高速自转的同时，其自身对称轴还绕竖直轴做回旋运动。如将飞轮转轴的自由端放在固定的竖直杆顶端的凹槽O中，使飞轮绕自身水平轴OO'旋转［5］，亦称之为自旋。放手后，飞轮在自旋的同时，其轴在水平面内以O为中心旋转。下面研究自行车飞轮进动的角动量。

3.动量与角动量知识的区别与联系

当一质点对参考点的动量守恒时，它的角动量必定守恒；反之，它对参考点的角动量守恒时，动量不一定守恒［6］。下面将进行具体证明：

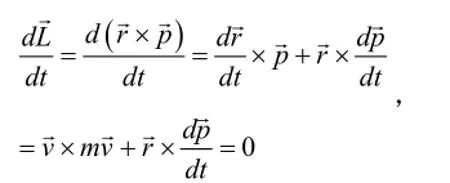
4.角动量知识的应用

4.1.解释日常现象［7］：

日常生活中很多现象蕴含角动量知识，如：滑冰运动员做花样动作时，合外力矩为0，角动量守恒，运动员通过伸展或收缩手臂及腿来改变自身对转动轴的转动惯量，从而改变转速。竞技运动员空翻时，在空中蜷缩身体减小转动惯量，增大转速；着地时伸展身体增大转动惯量，减小转速。

4.2.解题应用

4.2.1.证明定律：

行星运动的开普勒第二定律：在太阳系中行星对太阳的矢径在相等的时间内扫过的面积相等。现在我们通过角动量守恒定律来证明：

设质量为m的行星在t时刻速度为v→，对太阳的矢径为r→，因为行星对太阳的角动量守恒，所以恒矢量，行星对太阳的矢径在dt间隔内扫过的面积为：

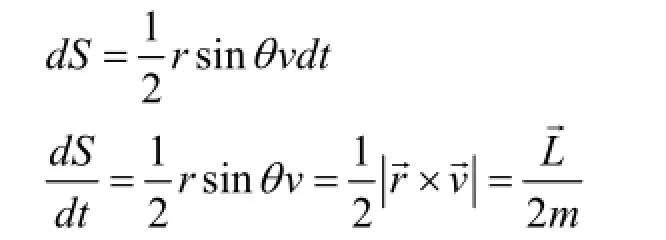
4.2.2.解题举例：

质量为m，长度为l的棒竖直悬挂于固定点，一质量为0m的子弹以水平速度0v→射入棒的下端后速度变为原来的，求子弹射出后棒的角速度ω。

分析：将棒和子弹视为一个系统，那么系统所受合力矩为0，满足角动量守恒：

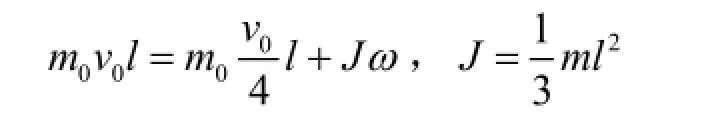
4.3.现代技术中的应用

角动量定理和守恒定律在现代技术如航空航天、航海、测量仪器等方面都有广泛的应用［8］。如航空方面：直升机为什么要安装抗扭螺旋桨呢？下面进行具体分析：直升机由三部分组成：主螺旋桨、机身和抗扭螺旋桨组成。将机身和主螺旋桨视为一系统，开始发动机没有发动，直升机静止，对于机身和主螺旋桨这一系统而言，角动量为零。主螺旋桨转动时，轮与地面的摩擦力矩为外力矩，系统的角动量增加，但此时主螺旋桨作用于机身的内力矩和轮与地面的摩擦力矩平衡，从而使机身处于平衡状态。随着主螺旋桨转速增加，机身离地，摩擦力矩为0，忽略空气阻力矩，系统角动量守恒，如果其转速继续增加，机身会向反方向运动，以维持角动量守恒，所以安装抗扭螺旋桨产生附加力矩与机身内力矩保持平衡。再如，轮船具有大量转动部件物体，当轮船航行时，轮船本身会绕横轴摆动，或绕铅直转弯或绕船身纵轴摆动，此时转动部件进动，从而产生陀螺力矩，造成轴承破坏或转轴弯曲。

［1］罗会琴.在物理教学中培养学生的发掘探究能力［J］.铜仁学院学报，2007，9（4）：128-130.

［2］陈文灯，黄先开.数学题型集粹与练习题集（理工类）［M］.北京：世界图书出版公司，2003.

［3］任丽英.关于力矩和角动量教学的几点看法［J］.忻州师范学院学报，2003，19（2）：69-70.

［3］王少杰，顾牡.新编基础物理学（上册）［M］.北京：科学出版社，2009.

［4］黄英，李华，李静.刚体角动量的确定［J］.职业圈，2007，（7）：117-119.

［5］张三慧.大学物理学：力学［M］.北京：清华大学出版社，1999.

［6］李志民.角动量守恒定律讨论［J］.洛阳大学学报，1999，14（2）：125-128.

［7］樊丽娟，张林，谭德斌，等.“物理问题”教学的实验研究［J］.铜仁学院学报，2010，12（4）：135-137.

［8］王志刚，张立换，徐建军.角动量理论在现代技术中的应用［J］.现代物理知识，2007，19（1）：87-90.

Theoretical Studies on Angular Momentum

YIN Fen-fen
（School of Continuing Education，Tongren University，Tongren，Guizhou 554300，China ）

In physics，mass points or mass point systems may revolve relative to the reference point or around the axis. In this case，neither velocity nor momentum can solve it，but angular momentum，a new physical concept of physics，is introduced，which precisely describes the revolution of an object，reflects its representational state in the quantum realm，and is therefore widely used in modern technologies. Based on the definition of angular momentum，this article studies the angular momentum theorems and the conservation laws governing in different circumstances such as the mass point relative to the reference point，the mass point around the fixed axis，the mass point system around the fixed axis，etc，and further probes the differences and commonality between momentum conservation and angular momentum conservation，and the application of angular momentum.

angular momentum，mass point，revolve

O311.1

A

1673-9639 （2015） 04-0098-04

（责任编辑 徐松金）（责任校对 毛志）（英文编辑 田兴斌）

2014-11-27

尹芬芬（1987-），女，湖南邵阳人，硕士，主要从事理论物理引力与相对论方向的研究。