一个定积分不等式的八种证明方法

庄科俊

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030 ）

一个定积分不等式的八种证明方法

庄科俊

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030 ）

对一个定积分不等式，通过八种证明方法阐明了定积分不等式证明中的一些方法及技巧。

定积分；不等式；积分中值定理；积分上限函数

1.引言

定积分不等式是数学分析的重要组成部分，对数学类专业学生后续课程的学习有着深远的影响。定积分不等式的证明方法和技巧非常灵活和多样，需要学生在学习过程中不断探索和总结。有不少文献对一些特殊的定积分不等式的证明做出了探讨［1-3］。本文针对哈尔滨工业大学2003年考研题中的一个定积分不等式的证明题，利用八种不同的方法进行了证明，借此阐明定积分不等式证明中的常用方法及技巧。

2.定积分不等式的证明

问题：设f（x）在［0，1］上连续且单调增加，证明：

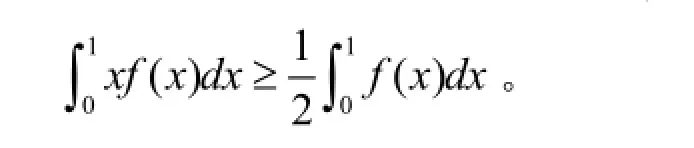
下面利用不同的知识，构建了八种不同的证明方法。

2.1.利用定积分定义

由于函数xf（x）与f（x）在［0，1］上都可积，所以可以选取等份分割T ：

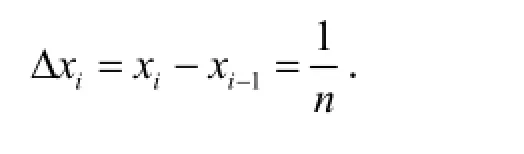
根据f（x）的单调性，对充分大的n，则有

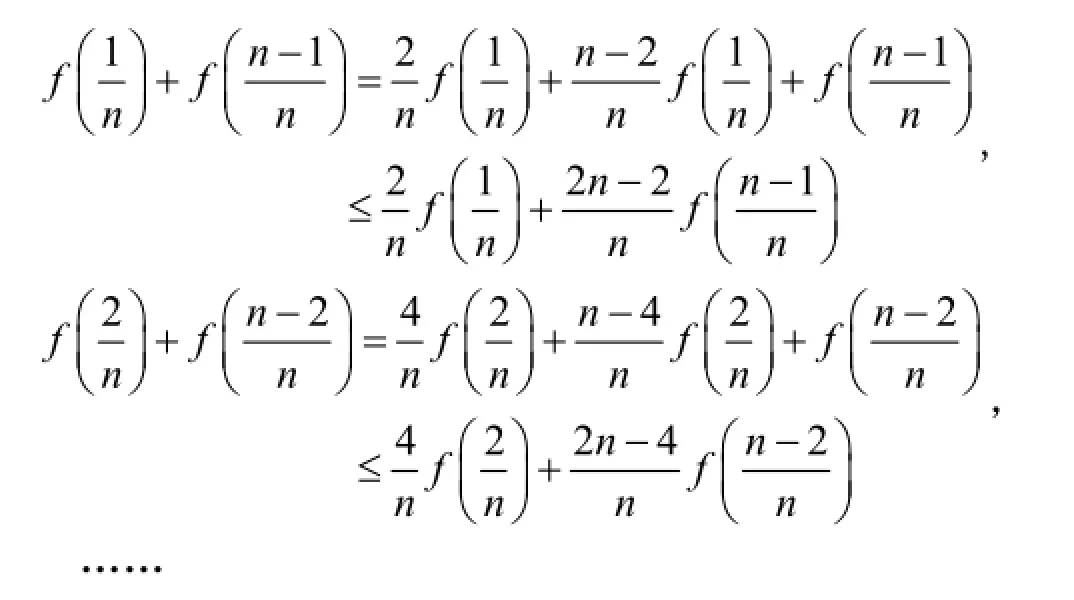
不论n是奇数还是偶数，总有

令n→∞，根据定积分的定义不等式得证。

2.2.利用换元法

作变换t=x2，则

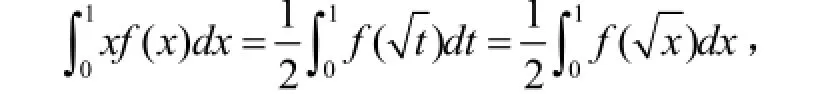
2.3.利用二重积分

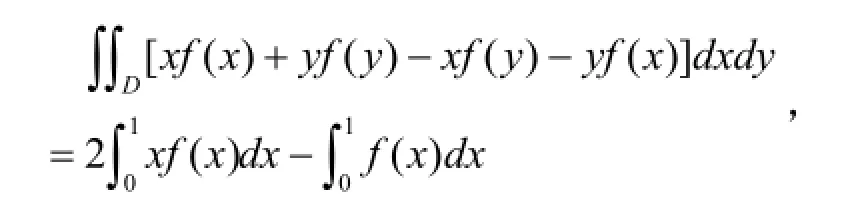
从而得证。

2.4.利用函数单调性

2.5.利用微分中值定理

2.6.利用积分第一中值定理

2.7.利用推广的积分第一中值定理

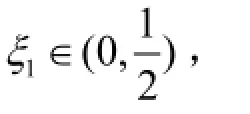
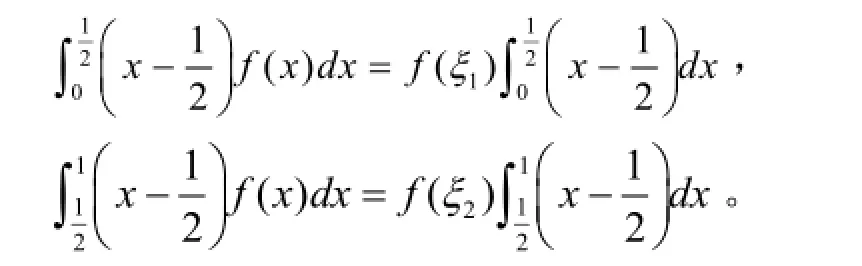
2.8.利用积分第二中值定理

利用积分第二中值定理的推论［4］，存在，使得

由函数f（x）的单调递增以及0＜ξ＜1，则

，可得

。证毕。

［1］殷剑峰.一些特殊积分不等式证明的探讨［J］.兰州文理学院学报（自然科学版），2014：28（1）：23-26.

［2］海杰.一道积分不等式的四种证法［J］.高等数学研究，2012，15（6）：46-47.

［3］蒋永锋.关于积分不等式的几种证明方法［J］.高等数学研究，2012，15（6）：53-55.

［4］华东师范大学数学系.数学分析（上册）［M］.第四版.北京：高等教育出版社，2010.

（School of Statistics and Applied Mathematics，Anhui University of Finance and Economics，Bengbu，Anhui 233030，China ）

Eight Proofs for an Integral Inequality

ZHUANG Ke-jun

In the paper，in order to prove an integral inequality，some common methods and techniques are illustrated by eight proofs for an integral inequality.

definite integral，inequality，integral mean value theorem，integral upper limit function

O172.2

A

1673-9639 （2015） 04-0188-02

（责任编辑 毛志）（责任校对 徐松金）（英文编辑 田兴斌）

2014-08-15

本文系安徽财经大学教学研究项目（acjyyb2014090）研究成果。

庄科俊（1982-），男，江苏金坛人，讲师，硕士，主要从事微分方程的研究。