有感于“老师，请别再抱怨”

杜继渠

“老师，请别再抱怨！”这是恳请？是劝解？是慰藉？是无奈？其中的苦辣酸甜，教师理当明白.从感情上讲，教师不厌其烦地把最好的方法、最能得分的手段无私“奉献”给学生，考不好怎能不抱怨？讲了就该懂，懂了就该会，会了就该对，为什么还老出错？可转念一想，学生何尝不想做对？他们本来就已自责，抱怨只会使其更加郁闷，解决不了实际问题.既然抱怨无助于问题解决，那就不再抱怨，向前看，找对策，反省“是不是要求过于严苛？”反思“讲了，为什么不懂？懂了，为什么不会？会了，为什么不对？”

一、“讲”与“懂”

从逻辑上讲，“懂”是“会”的必要条件，“会”是“对”的必要条件，那么，“讲”是“懂”的什么条件？是充分条件，还是必要条件？在没有回答这个问题之前，请先看一个教学案例.在向量习题课，备课组编制了这样一道题.

问题1：“设点O是△ABC的三边中垂线的交点（如图1），且AC2-2AC+AB2=0，则·的取值范围是 .”要求将课堂还给学生，自主探究.下面就“同题异构”的不同处理加以分析.

1.教师甲执行“把课堂还给学生”.于是找学生A到办公室培训，A哪里能瞬间反应过来，一时间不知所措，于是教师就把自己的做法讲给学生，然后让学生A到课堂上讲：

因为OH⊥BC，所以·=0，于是·=（+）=·，又因=-，=（+），所以·=（-）*.由AC2-2AC+AB2=0得，AB2=2AC-AC2，代入*式，得·=AC2-AC，因AB2>0，解得AC∈（0，2），从而解得·∈[-，2）.

点评：这样的“讲”是“懂”的什么条件？能有几位听得懂？不要说其他同学云里雾里，就说学生A，也只是个教师的“传话筒”，自己都没搞明白，何以说服别人？效果可想而知，更经不起“是怎么想到的？”的质问.

2.教师乙改善了处理方式.他在讲解之前提出4个问题：①与在上的投影相同吗？②因为O是外心，H为BC中点，所以OH与BC是什么关系？③为什么选择，为基底？④怎么想到求AC取值范围的？学生思考后，教师讲解顺利，懂的人数明显增多.

点评：和教师甲比较，教师乙的意图很明显，就是奔着“懂”字设计的.通过问题①引导学生将·转化为·；通过问题②引导学生将与分解；通过问题③引导学生获得基底，的表达式；通过问题④引导学生从条件AC2-2AC+AB2=0获得AC的取值范围，可谓一步一个脚印.遗憾的是，这些问题都是教师提出的，学生被教师牵着鼻子走，没有理解“为什么要设计这4个问题”.

3.教师丙是基于解题信息原理设计的.他要学生从题目条件中挖掘信息资源，讨论后，小组提供的信息是：①因为点O是外心，连结O与BC中点H，OH⊥BC，有·=0；②因为+=，所以·=·；③因为H是BC中点，所以=；④基于AC2-2AC+AB2=0的结构，想到用，表示，；⑤再由AB2>0确定AC的取值范围，最后求出·的取值范围.

点评：信息挖掘的过程，既是寻找解题突破口的过程，也是梳理解题算法的过程.新课标将“信息收集，数据处理”列为数学课程目标，显然，教师丙关注了这一目标，并将课堂话语权交给了学生，这无疑激发了学生探索的热情.至此，即便教师不讲，学生也能通过合作解决这一问题.你说“讲”是“懂”的什么条件？

4.教师丁又有自己的做法.他让学生揣摩命题者心理.学生经过独立思考，小组讨论，提出问题：①在外心上做文章，目的何在呢？外心和中点有紧密联系，难道想在中线上找事？②中线向量与对应边的向量之积其实就是对角线向量之积，难道想用AB，AC两边对应的向量表示？③给出AC2-2AC+AB2=0有什么价值呢？经历这样一连串发问，学生逐渐意识到命题意图，当回过头审视的时候，感觉命题者的出发点就在于此.

下面是两位同学对命题心理的大胆揣测：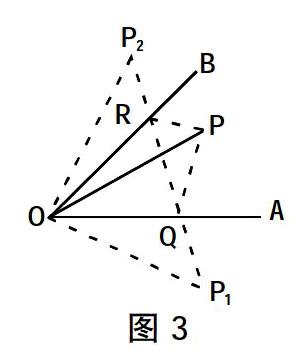

第一位同学：“我想设计一个求-类问题，一来想在转化上做文章.给一个条件AC2-2AC+AB2=0有两方面作用：明线——化二元AC，AB为一元AC，暗线——利用AB2>0求AC的取值范围；二来想在结构（+）（-）上做文章.因=，且与在上的投影相同，将求·变为求·.这样，一道向量题就新鲜出炉了.”

第二位同学：“本想在重心上做文章，‘设点G是△ABC的重心，且AC2-2AC+AB2=0，则·的取值范围是 .发现目标太显然，所以增加点隐蔽性，就改为‘外心吧.”

点评：如果说懂得解法是“懂题”，那么，揣测命题心理就是“懂你”，能够与命题者对话，并产生心理共鸣，对于把握问题本质是非常关键的，无论学生揣测得对与不对，至少学生有他自己的认知思考，这种习惯养成对于促进元认知能力发展，非常关键.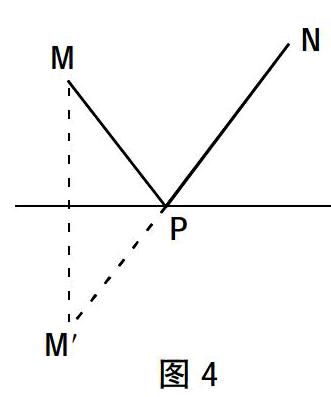

反思：同一问题，教师不同，处理方式不同，说明了他们对“讲”与“懂”的关系理解程度不同.教师甲让学生A做“传话筒”，完全忽视了学生的感受，这样的课堂不还给学生也罢，抱怨学生没有理由；教师乙通过提问让学生顺着自己的思路前行，虽然比教师甲有所进步，但还是牵着学生的鼻子走，没有大胆放手，即使学生不懂，也不该抱怨什么，因为目标在“懂”而未能真懂；教师丙比教师乙放得开，显示了教师丙对学生的充分信任，取得的效果显然优于前者，学生既已达到预定目标，教师这时只有赞赏的份，哪还有抱怨；更可贵的是，教师丁让学生揣摩命题者意图，这是解题教学的更高境界，是在玩味数学，欣赏数学，与命题者进行心灵对话是一种享受，也许学生想的比命题者想的还多，那便有利于优化的思维，正应了郑毓信教授在《数学教育改革十五诫》中阐明的观点“数学教学不应只是提‘算法多样化，但却完全不提‘必要的优化”.思维从收敛转向发散，发散后再优化，就能融会贯通.endprint

至此，你认为“讲”是“懂”的什么条件？基于以上案例分析，笔者认为，是既不充分也不必要条件.“讲”，要考虑“when， where， who， how”，将课堂还给学生，不能忽视教师的主导作用，该教师讲的，理直气壮地讲，不过，教师的“讲”，要有启发性，示范性，针对性，联系性，适切性.不仅是方法、思想，还有问题结构，命题智慧，等等.通过示范，要让学生感受到，我们不光是一个解题者，还是鉴赏者，开发者，研究者，思想者.鉴于此，笔者坦言，一个解题教学优秀的教师，在其他课型的教学上，也是优秀的，因为他总是那么关注主体，那么适切！

二、“懂”与“会”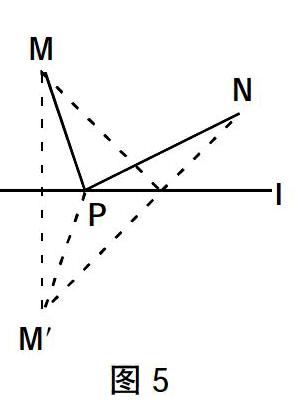

《现代汉语词典》中的“懂”是知道，了解；“会”是什么意思？理解，领悟.那么，“懂”是“会”的什么条件？笔者认为，“懂”是“会”的必要条件，“懂”是“会”的一种可能性，学生听懂了，那说明他可以接受，但仍然会“游离”在门外，跨不进“会”的门槛.这好比跳水，光看人家动作娴熟，轻灵一跳，顺利完成，若摊到自己，真的是那回事吗？当有“必须成功”的压力存在，难道就不自乱方寸？依笔者见，“懂”与“会”之间远隔“万水千山”，就像玄奘“梦想取经”和“取经归来”，中间经历重重磨难，认为唾手可得而异想天开的“穿越”，是逃避现实.要将“可能性”变为“现实性”，处理好“懂”与“会”的关系，师生都要下一番苦功夫.

从集合论观点分析（如图2），“会”是“懂”的一个子集，“会”关于“懂”的补集就是“懂而不会”，补集的成分越大，“会”的成色越差，也是我们教师最为担忧的，研究“懂而不会”现象，一线教师有优势，也有责任.

问题2：在△OAB中，OA=3，OB=4，AB=5， P是OA中点，M，N分别是AB，OB上的动点，求△PMN周长的最小值.在初中，学生曾见过类似的问题.

问题3：如图3，∠AOB=45°，P是∠AOB内一点，PO=10，Q，R分别是OA，OB上的动点，求△PQR周长的最小值.

对于这一问题，只要作出点P关于直线OA，OB两个对称点P1，P2，线段P1P2长就是△PQR周长的最小值.要想求P1P2长不难，因为∠P1OP2=90°，利用勾股定理求得周长的最小值为10.

而对于问题2，不知∠OBA具体值怎么办呢？有效的办法就是将三角形置入直角坐标系中，先代数化；或利用二倍角公式及余弦定理.这样的一道题放在高二，应该不难求解，然而，错误率竟过半.鉴于此，教师进行访谈.

先访谈犯错同学.

师：初中曾见过类似的问题吗？

生1：想不起来.

师：是否见过问题4？如图4，在定直线l上求作一点P，使P到两定点M，N距离之和最小？

生2：见过，在初中处理过这样的问题.

后访谈答对同学.

师：曾见过类似问题吗？

生3：见过，在初中.

看来，初中基础对于高中阶段学习影响很大.真正拥有初中解题经验的学生，马上会意识到“对称”，于是通过作图找到两个对称点，求出两点间距离即为周长的最小值.

访谈之后笔者思考，即便对问题3没有印象，但对于问题4不会没有印象吧，这可是具有物理背景的“镜面反射”问题，人人皆知，为什么学生不能借助问题4的方法处理问题2呢？进一步交流发现，学生虽懂得问题4，但没有真正领会“化曲为直”的思想，也就是在求多边形周长最值的时候，想不到将封闭“图形”打开.

在初中，教师如能系统理解这一类问题及其一以贯之的思想方法，就会高度关注问题4的教学.借助几何画板，拖动图5中点P，学生就会发现，虽然点P在直线l上移动，M，N两点关于直线l的对称点不变，利用这一性质，我们就能将PM转移到PM′，随着动点P的移动，学生会直观地发现折线M′PN不断变化，最小值出现在三点一线之时.

在变化中寻找不变性，是科学研究的一般方法.我们经常提问学生：“懂了吗？”“懂了！”“会了？”“会了！”甚至有学生认为，后面一问多余，在他们看来“‘懂就等于‘会”，这其实还是教师观念造成的.

点评：教师引领，不是拖着学生向前走，要善于驻足，等待“后面梯队”，“驻足”不是沉默，无声无息地等待，而是启发“先头部队”做有意义的事，比如一对一帮扶，进一步思考，变式拓展，对比辨析等.下面对问题4和问题2作以辨析.

问题4中已知“两个定点，一个定直线”，要解决的问题“线段和最小”，实质可转化为“三角形周长最小值”问题（因为两个定点距离是确定的）.问题2中已知“一个定点，两条定直线”，要解决的问题也是“三角形周长最小值”问题.这里，不变因素是“对称点”，思想方法是“化曲为直”，遵循原理是“两点之间线段最短”.通过对比辨析，我们获得了解决这一类问题的基本方法，这种看似技巧而不是技巧的原理是解决问题的“经验模块”.

三、“会”与“对”

“懂”偏向于“方法、技能”，“会”偏向于“思想、意识”；“懂”起步于“了解”，“会”趋向于“贯通”；“懂” 意味着 “有望”，“会”饱含着“希望”.但要把希望变成成功的现实，还要关注“会”与“对”.“会”又是“对”的必要条件.

我们经常问学生：“这样的题你会做吗？”“会！”可做出来的结果却不尽如人意，或丢掉点什么，或数据处理不当.面对这样的问题，我们自问：“会了为什么做不对？”这种非常普遍的“会而不对”现象时常困扰着一线教师.

目前，高考命题更多关注基础（基础题过半），甚至出现相当数量的送分题，只要学生做到“会且对”，拿一百多分不算难事.然而阅卷发现，前6题就开始出错，“心算失误”.如求“1+2+3+…+（n-1）”，有人就把最前面的1搬到最后，与n-1合并为n，变为求“2+3+…+n”，根据求和公式解得Sn=.出现这种现象，难道是因为不会？不是，会了，却心算失误，这是应试心理问题.endprint

为了赶时间，紧张答题演变为慌张答题，觉得稍微简单就口算，忙中出错.若稍加留意，你会发现调整后的数列已不再是等差数列，因为原数列变成“2，3，4，…，n-3，n-2，n”，再当成等差数列处理，岂有不错之理？像这样心算失误并不孤立.

再看数学卷7～12题，相比前6题，错误率明显攀升，是不是学生不会呢？不全是，很多是忽视细节所致.如“已知O为△ABC的外心，若5+12-13=0，则C= .”学生从“外心”及系数特征找到了解题突破口，移项（移-13到右边）再平方，得到了·=0，于是由圆心角∠AOB=90°，得∠C=45°.问题出在哪里？学生作图（如图6）误导，以为外心在三角形内部，根据“同弧所对圆周角度数是圆心角度数的一半”得∠C=45°，其实学生忽视了13=5+12，原来∠C=135°.

点评：把会做的题做对，说来容易，做起来难，要想学生少出错，务必要培养学生解题反思的习惯，把“思维策略”和“注意事项”结合起来，关注细节，关注易错点，避开“陷阱”，才能实现“会而且对”.再看数学卷15～17题，考查双基、重点，命题出发点是让学生在这里得到基础分，但事与愿违，往往错误率比想象的高，“会而不对”形势严峻.鉴于此，笔者认为，抓住数学试卷的15～17题，开展“会而不对”的研究.

感言：教室是学生犯错的地方，学生作为学习主体，必须经历该有的经历，品尝从失败走向成功的酸甜苦辣，品味学习的痛苦与快乐，历练心智.没有谁可以剥夺学生这种必要的体验，教师更没有必要抱怨学生.事出都有因，认真查找出事的原因，变错误为资源，以此促进学生深刻反思，这不仅不是件坏事，反而是教师积极影响学生的好机会，是拉近师生情感距离的契机，因“犯错”获得的教育素材，比“预防”更有针对性，更有价值.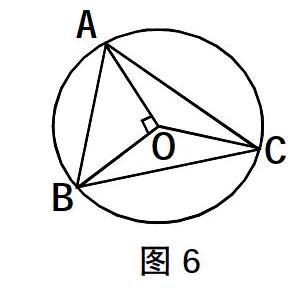

任何知识的领会都难免掺有“杂质”或“垃圾”，这不要紧. 自然界没有“纯氧”，而当我们需要氧气的时候，我们只能面对现实，吸入二氧化碳和有害气体. 知识的汲取同样如此，任何概念，都是在纷繁复杂的自然现象中剥离出来的理想化模型，看似出淤泥而不染，其实经历千锤百炼，逐步提纯、萃取、调整、重构，才一天天成熟起来. 科学家尚且如此，十多岁的孩子，怎么就一定是顺顺当当？

要知道，学习是学生自己的事，教师的抱怨，有时不仅不能促进学生正确的意识，反而产生对立情绪，一旦形成这种局面，抱怨将危害双方，阻碍正常对话.最好的方式就是坐下来，心平气和地同学生一起分析犯错的原因，甚至要为学生辩护，谈自己学生时代的犯错故事，笔者曾在《中学数学》发表文章“为学生寻找做不出的理由”，就是基于这样的认识而产生的灵感，这样的姿态不仅不会削弱教师在学生心目中的地位，相反，会赢得学生的爱戴！

事实上，当你以朋友的姿态坐在孩子面前，研究错因，寻找对策的时候，是学生无比幸福的时光，他从你的精彩评论中得到启迪、激励和安慰，在你帮助他树立自信心的过程中，产生学好数学的信念.endprint