高动态弱直扩信号的分级捕获算法*

董 良，马正新，王毓晗

(清华大学电子工程系，北京100084)

1 引言

目前直接序列扩频技术(Direct Sequence Spread Spectrum，DSSS)在军事、移动和卫星通信中得到了广泛应用，在某些特殊的环境下，接收信号具有低信噪比和大多普勒频偏的特点，给接收机实现伪码捕获和载波多普勒频偏估计增加了难度。

针对上述低信噪比高动态的情况，实际中常用的捕获算法有相干积分+非相干累加、相干积分+差分相干累加和PMF－FFT(Partial Match Filter－Fast Fourier Transform)+非相干累加等算法。文献[1－2]中将相干积分结果平方后进行非相干累加，在获得能量积累的同时，也带来平方损耗，尤其存在较大多普勒频偏时，捕获效果并不理想。文献[3－4]中通过对相干积分结果进行差分相干累加，减小平方损耗，获得比非相干累加更大的增益，但在多普勒频偏较大的情况下，捕获性能急剧恶化。文献[5－7]采用基于PMF－FFT的非相干累加(PMFFFT－EMDS)捕获算法，能够同时对伪码相位和多普勒频偏进行搜索，减少了捕获时间，能够在一定程度上减小多普勒频偏对相干积分增益的影响。通过增大部分匹配滤波器长度和FFT运算点数可以提高PMF－FFT－EMDS算法的频偏估计精度，但在多普勒频偏很大的情况下，增大部分匹配滤波器长度会导致相干积分增益快速下降，而FFT运算点数的增大对数字处理器提出更高要求，在实际应用中受到限制。受大多普勒频偏和调制数据位跳变的影响，PMF－FFT－EMDS算法难以有效提高多普勒频偏估计精度，而较大的残余多普勒频偏将直接影响后面跟踪环的跟踪性能。

针对常用高动态弱信号捕获算法在多普勒频偏估计精度上的不足，本文对PMF－FFT－EMDS捕获算法进行改进，提出了一种基于频偏补偿的高动态弱信号分级捕获算法，即利用第一级系统的载波频偏粗估值对多普勒频偏进行补偿，并在第二级系统中采用滑动平均修正算法[6]消除调制数据位跳变对FFT频谱的影响，有效提高了频偏估计精度。仿真结果表明，在不增加FFT运算点数的前提下，该算法可以实现伪码相位快速捕获并提高多普勒频偏估计精度，同时具有算法实现简单的特点。

2 经典PMF－FFT－EMDS捕获算法

将接收到的中频信号数字下变频并经过低通滤波器得到基带信号，其复数表达式为

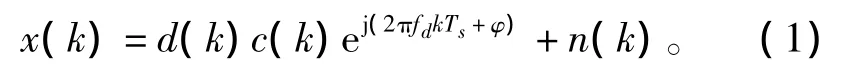
式中，d(k)为调制数据;c(k)为伪码序列;fd为多普勒频偏;Ts为采样间隔，本文取为伪码的码片周期;φ为载波初始相位;n(k)为叠加的复高斯白噪声。

为分析方便，假设本地伪码与接收信号伪码相位已对齐且不考虑噪声情况，此时PMF－FFT结构第K点FFT输出的归一化幅频响应[5，8]

式中，fd为多普勒频偏;M为伪码码长;X为部分匹配滤波器长度;P为部分匹配滤波器个数，P=M/X;N为FFT点数(N≥P，一般取N=P)。通过上面分析可知，该算法的频率分辨率Δf为

当接收信号信噪比很低时，仅通过PMF－FFT算法获得的增益无法实现频谱峰值正确检测，需采用非相干累加方法进一步提高信噪比。非相干累加方法使得积分时间不受调制数据符号跳变的影响，对PMF－FFT输出结果Gr(fd，k)取模的平方并进行非相干累加，得[5]

式中，L表示非相干累加次数。如果珋I[k]中最大值超过预设门限，则判定捕获成功。非相干累加在获得增益的同时也会带来平方损耗[9]，使得提高信噪比能力有所降低。平方损耗随着相干积分输出信噪比的增加逐渐降低[10]，通过提高非相干累加前的信噪比可以减少平方损耗，从而提高非相干累加后的增益。

3 基于频偏补偿的改进算法

3.1 多普勒频偏对信号捕获的影响

在低信噪比高动态环境下，接收信号存在较大的多普勒频偏，由式(2)可知，随着频偏的增大，系统输出增益衰减增大，对捕获性能产生较大影响。设 M=1024，码片速率 Rc=6.144 Mbit/s，图 1 给出了在不同的匹配滤波器长度X和FFT点数N下，多普勒频偏对幅频响应的影响。

图1 多普勒频偏对幅频响应的影响Fig.1 The effect of Doppler frequency offset on amplitude－frequency response

如图1所示，在部分匹配滤波器长度一定的情况下，多普勒频偏越大相关损失越大;在多普勒频偏一定的情况下，部分匹配滤波器越长相关损失越大。由式(3)可知，提高频偏估计精度需通过增加部分匹配滤波器长度X或增大FFT点数N。当存在大多普勒频偏时，增加部分匹配滤波器长度X会导致相关增益严重恶化;FFT运算使得信号的频谱分散在N个离散点上，当真实多普勒频偏位于两根FFT谱线之间时，多普勒频偏估计值与真实值将存在误差，误差范围为Δf/2，增大FFT运算点数N能够减小误差范围，提高频偏估计精度，但同时也对数字处理器件的运算速度提出更高的要求，此方法在实际应用中受到一定的限制。

3.2 调制数据对信号捕获的影响

在对直扩信号进行捕获的过程中，相干积分时间内调制数据位跳变将严重影响捕获性能。设接收信号与本地伪码对齐相乘后得

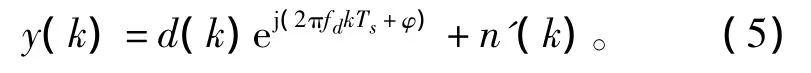
为分析方便，不考虑噪声和载波初始相位，由上式可知，ej(2πfdkTs)的频谱为冲激函数 2πδ(f－ fd)，则 y(k)的频谱为d(k)频谱的线性搬移，也就是说d(k)决定了y(k)频谱的形状[5－6]。当PMF输出个数P不变时，增大部分匹配滤波器长度X，则PMF－FFT分析数据长度ML将大于一个伪码周期M，若不存在调制数据跳变，即d(k)保持不变时，FFT谱分析输出为单一谱峰;如存在调制数据跳变，则会造成频谱扩散，不再是单一谱峰，同时谱峰幅度也会减小，严重影响谱峰检测性能。以分析数据长度ML等于4个数据码元为例，对调制数据跳变不同情况进行FFT谱分析，部分仿真结果如图2所示。

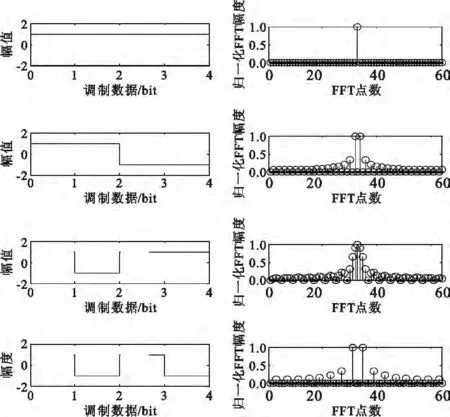
图2 调制数据跳变的FFT频谱分析图Fig.2 Spectrum analysis of modulated data

3.3 基于频偏补偿的两级PMF－FFT－EMDS捕获算法

在低信噪比高动态环境下，PMF－FFT－EMDS算法受到大多普勒频偏和调制数据限制，对捕获性能的影响主要反映在两方面:一是大多普勒频偏限制了部分匹配滤波器长度，在FFT运算点数一定的情况下，难以提高频率分辨率;二是受调制数据位跳变的影响，PMF－FFT相干积分时间限制在一个调制数据内，难以进一步提高相干积分增益以减少非相干累加过程中的平方损耗，又由式(3)可知，同时对频率分辨率的提高产生限制。

基于上述问题，为了提高多普勒频偏估计精度，本文在不增加FFT运算点数的前提下提出一种基于频偏补偿的两级PMF－FFT－EMDS捕获算法，该算法通过在第二级相干积分前进行频偏补偿，可以有效减小多普勒频偏，通过调整部分匹配滤波器长度X并利用滑动平均窗消除调制数据位跳变的影响，从而提高频偏估计精度。两级 PMF－FFTEMDS捕获算法原理如图3所示。

图3 基于频偏补偿的两级捕获算法Fig.3 Two － stage acquisition algorithm based on frequency offset compensation

具体算法流程如下:

(1)基带信号X(K)如式(1)所示，将X(K)送至第一级PMF－FFT－EMDS中进行处理，首先通过P个部分匹配滤波器与本地伪码进行相关，部分匹配滤波器长度为x1，对P个部分匹配滤波器输出值进行N点FFT运算(N≥P)，考虑到调制数据位跳变的影响，一般PMF－FFT分析信号长度不超过一个调制数据码元宽度，本文取N=P，然后将PMFFFT输出值进行L1次非相干累加，当非相干累加后输出峰值超过预设门限时，判断接收信号X(K)的伪码与本地伪码初步对齐(相位差小于1个码片)，可获得伪码粗同步值和多普勒频偏粗估值;

(2)根据步骤1获得的伪码相位粗同步值和多普勒频偏粗估值，调整本地伪码相位使其与接收信号基本对齐，并利用频偏粗估值对多普勒频偏进行补偿，可得

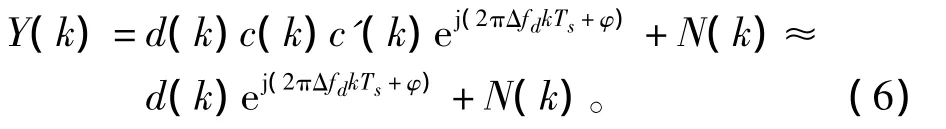
式中，c'(k)为调整后的本地伪码，Δfd为残余多普勒频偏，N(k)为复高斯白噪声;

(3)将Y(k)送至第二级PMF－FFT－EMDS中进行处理，调整部分匹配滤波器长度x2=x1n，FFT运算点数为N，非相干累加次数L2，非相干累加后频谱为YFFT(K)。由式(3)可知，通过调整部分匹配滤波器长度，PMF－FFT分析信号长度变为n个调制数据码元，第二级频偏估计精度相比第一级提高了n倍，同时两级FFT运算点数均为N，在工程应用中还可以实现FFT资源复用;

(4)利用滑动平均窗对频谱YFFT(K)进行修正。调制数据跳变会引起FFT频谱扩散，但频谱能量仍主要集中在Δfd周围，即Δfd周围的能量谱之和近似等于y(k)的能量。通过滑动平均窗对频谱进行处理，使得峰值检测量变为Δfd周围能量谱之和的均值，在消除频谱扩散的同时对峰值周围的噪声功率起到平滑作用，改善了谱峰检测性能。设滑动窗口长度为J，则经修正后输出结果为[6]

文献[6]进一步对工程实践中滑动窗口大小进行设计，J应满足

式中，J为滑动窗口长度，Rb为调制数据速率，Δf为搜索精度。最后，根据Imov(K)中频谱最大值所对应的位置Kmax，可以得到残余多普勒频偏估计值Δfd'。

4 仿真分析

为检验改进算法的性能，利用MATLAB进行仿真实验。仿真参数设置如下:调制数据速率Rb为6 kbit/s，伪码长度M为1024，一个调制数据对应一个伪码周期，则伪码码片速率 Rc为6.144 Mbit/s。经典PMF－FFT－EMDS捕获算法中部分匹配滤波器长度X1=64，FFT点数 N1=64，则 PMF－FFT分析信号长度为4096个伪码码片(假设调制数据无跳变)，非相干累加长度L1=16;本文所提算法第一级PMF－FFT－EMDS中X2=16，N2=64，L2=64，第二级PMF－FFT－EMDS中 X3=64，N3=64，L3=16，滑动平均窗长度J=5。

4.1 捕获精度和捕获范围

由式(3)可知，本文所提算法的频率分辨率为Δf=1/XNTs，则PMF－FFT分析信号的长度决定算法的频偏估计精度，且分析信号越长，精度越高[11]。通过设置合适的部分匹配滤波器长度X和FFT运算点数N，可以提高多普勒频偏估计精度，使其满足后续跟踪环路的要求。仿真中本文所提算法第一级频率分辨率为Δf1=6 kHz，经过频偏补偿后第二级频率分辨率为Δf2=1.5 kHz，捕获精度提高了4倍。

当捕获算法的频率分辨率Δf确定时，根据FFT运算点数N可以确定多普勒频偏的单边带捕获范围:

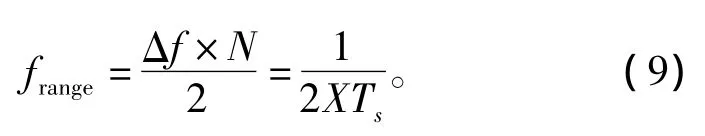
则双边带捕获范围为－frange～+frange。在高动态环境下部分匹配滤波器会引起较大的相关损失，一般根据实际情况选取frange的一部分作为实际单边带捕获范围。当多普勒频偏为 fmax时，frange需满足如下条件:

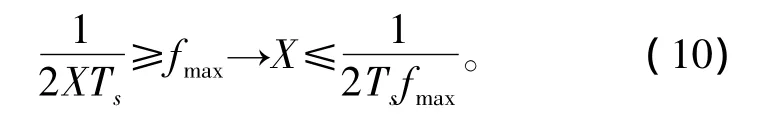
因此，应根据式(10)合理设计部分匹配滤波器长度X。由式(9)知，仿真中经典 PMF－FFTEMDS算法的单边带捕获范围为48 kHz，本文所提算法中第一级和第二级的单边带捕获范围分别为192 kHz和48 kHz。当捕获精度相同时，本文所提算法中第一级PMF－FFT结构的单边带捕获范围更大，有利于高动态环境下直扩信号的快速捕获。

4.2 检测概率

根据仿真参数设置，两种算法频偏估计精度相同且分析信号总长度相等，并假设经典PMF－FFT－EMDS算法在相干积分时间内无调制数据跳变，下面采用最大值检测准则[7]，对不同信噪比情况下多普勒频偏对检测概率Pd的影响进行仿真。

图4是多普勒频偏fd分别为30 kHz、42 kHz和48 kHz时，随着信噪比Eb/N0的变化，本文所提算法和经典PMF－FFT－EMDS算法检测概率Pd的变化情况。从图中可以看出，当信噪比从－4 dB到3 dB时，在不同多普勒频偏情况下两种算法的检测概率都随着信噪比增大而提高;当多普勒频偏 fd为30 kHz时，经典PMF－FFT－EMDS算法的检测性能优于本文所提算法，但随着fd的增大，经典算法的检测概率出现较大下降，低于本文所提算法，而本文所提算法受多普勒频偏影响较小，在捕获范围内多普勒频偏越大，检测性能优势越显著;对于相同检测概率，当fd为42 kHz时，本文所提算法比经典PMF－FFT－EMDS算法信噪比提高约0.5 dB，当 fd为48 kHz时，提高约1.5 dB。如果考虑到调制数据位跳变对经典算法检测概率的影响，本文所提算法的优势将更明显。

图4 改进算法与经典算法检测性能比较Fig.4 Comparison of the detection performance between the improved algorithm and the classical algorithm

5 结束语

本文研究了低信噪比高动态环境下直接序列扩频信号的快速捕获问题，在分析经典PMF－FFTEMDS算法的基础上，提出了一种基于频偏补偿的两级PMF－FFT－EMDS捕获算法。该算法通过频偏补偿减小多普勒频偏并利用滑动平均窗克服调制数据位跳变的影响，解决了多普勒频偏估计精度和FFT运算量的矛盾，有效地提高了频偏估计精度，适合工程实际应用。从仿真分析可以看出，本文所提算法在低动态环境下的检测性能低于经典PMFFFT－EMDS算法，但在高动态环境下具有明显的优势，而且频偏捕获范围更大，因此更适合低信噪比高动态环境下的直扩信号捕获。

[1]罗奎，程剑，李仰志，等.非相干累加中检波方式的性能分析与参数选取[J].电讯技术，2011，51(5):56－61.LUOKui，CHENG Jian，LI Yangzhi，et al.Performance A-nalysis and Parameters Selection of Detection Methods Based on Non － coherent Accumulation[J].Telecommunication Engineering，2011，51(5):56 －61.(in Chinese)

[2]张文明，周一宇，姜文利.GPS信号捕获性能的分析[J].系统工程与电子技术，2002，24(10):73 －75.ZHANG Wenming，ZHOU Yiyu，JIANG Wenli.Analysis of the Signal Acquisition Performance of the GPS[J].Systems Engineering and Electronics，2002，24(10):73 －75.(in Chinese)

[3]Wei Y.Selected GPS Receiver Enhancements for Weak Signal Acquisition and Tracking[D].Calgary，Alberta，Canada:The University of Calgary，2007.

[4]皮亦鸣，张婧，蔡昌听.GPS信号的差分相关捕获算法研究[J].全球定位系统，2006(4):1－4.PI Yiming，ZHANG Jing，CAI Changting.Research of Differential Correlation Acquisition Algorithm in GPS[J].GNNS World of China，2006(4):1 －4.(in Chinese)

[5]胡建波.高动态扩频信号快速捕获方法的研究[D].哈尔滨:哈尔滨工程大学，2005.HU Jianbo.Research on Fast Acquisition Method of High Dynamic DSSS Signals[D].Harbin:Harbin Engineering University，2005.(in Chinese)

[6]叶艳珠.卫星扩频测控快速捕获技术研究[D].北京:清华大学，2007.YE Yanzhu.Study on Rapid Acquisition Technology in DSSS － based Satellite TT＆C Systems[D].Beijing:Tsinghua University，2007.(in Chinese)

[7]秦勇，张邦宁，郭道省，等.低信噪比高动态条件下P码直接捕获技术研究[J].宇航学报，2009，30(2):760 －765.QIN Yong，ZHANG Bangning，GUO Daoxing，et al.Study on P－Code Direct Acquisition Technology in Low SNR and High － dynamic Environment[J].Journal of Astronautics，2009，30(2):760 －765.(in Chinese)

[8]何攀峰，程乃平，丁丹，等.高动态直扩信号快捕设计与 FPGA 实现[J].电讯技术，2014，54(5):547 －552.HE Panfeng，CHENG Naiping，DING Dan，et al.Fast Acquisition of High Dynamic DSSS Signal:Design and FPGA Implementation[J].Telecommunication Engineering，2014，54(5):547 －552.(in Chinese)

[9]邓强.一种改进的两级相干累加码捕获方法[J].电讯技术，2012，52(5):704 －708.DENG Qiang.An Improved Two－stage Coherent Accumulation PN Code Acquisition Method[J].Telecommunication Engineering，2012，52(5):704 －708.(in Chinese)

[10]梁林方.弱信号GPS接收机的捕获算法研究[D].成都:电子科技大学，2011.LIANG Linfang.Research of Acquisition Algorithm in GPS Receiver for Weak Signal[D].Chengdu:University of Electronic Science and Technology of China，2011.(in Chinese)

[11]周三文，黄龙，卢满宏.FFT在高动态扩频信号捕获中的应用[J].飞行器测控学报，2005，24(2):61 －64.ZHOU Sanwen，HUANG Long，LU Manhong.Acquisition of High Dynamic Spread Spectrum Signal with FFT[J].Journal of Spacecraft TT＆C Technology，2005，24(2):61 －64.(in Chinese)