改进的变步长维纳系统盲源分离方法*

赵立权，齐厚颖

(东北电力大学信息工程学院，吉林吉林132012)

1 引言

盲源分离(Blind Source Separation，BSS)是指在信源信号和信道参数都未知的条件下，从观测到的混合信号中估计出信源信号，被广泛用于多种信号处理和分析领域。目前的研究仍然主要集中于线性瞬时混合信号的盲源分离问题，但在许多的实际系统中，非线性混合模型更为常见。为此，近年来许多学者提出了非线性盲源分离问题。非线性盲源分离是一种针对非线性混合信号的盲源分离方法，已经被广泛应用于医学信号处理、通信信号处理、图像处理及故障诊断等方面[1－4]。目前具有代表性的非线性盲源分离方法主要有以下几类:一是基于互信息最小化的非线性盲源分离方法[5－7]，采用互信息作为衡量相互独立性的标准，互信息越小，分离效果越好;二是基于贝叶斯的非线性盲源分离方法[8－9]，成功利用贝叶斯网络理论处理非线性混合模型中各个变量和参数间的关系;三是基于参考信号的非线性盲源分离方法[10－11]，是一种运用信源信号的先验信息作为参考信号的分析方法以及基于线性盲源分离的非线性盲源分离方法，该方法是通过对观测数据进行高维映射，将非线性问题转化成线性问题[12－13]。

维纳系统被应用于信号处理、生物、金融、社会以及心理分析等多方面，针对盲源分离问题，研究学者提出了基于非线性盲源分离的维纳系统BSS方法[14－15]，该方法采用基于互信息最小化的非线性盲源分离方法对维纳系统中的信号进行盲源分离。为了克服固定步长非线性盲源分离算法收敛性能差的问题，本文提出基于变步长和马尔可夫原理的后置非线性盲源分离算法，提高维纳系统BSS的性能。

2 非线性BSS数学模型

假设n个相互独立的未知源信号s(t)=[s1(t)，s2(t)，…，sn(t)]T，首先经过未知的线性混合矩阵 A(n×n维)，得到线性混合信号 x(t)=[x1(t)，x2(t)，…，xn(t)]T=As(t)，再将 x(t)分别通过一个非线性混合系统 f=[f1，f2，…，fn]T，得到观测信号e(t):

盲源分离中的解混和混合是一个互逆的过程。此非线性混合系统的解混由两部分组成:第一部分是对非线性混合函数f的求逆，即它是一个非线性反变换函数 g=[g1，g2，…，gn]T，用来补偿混合过程中的非线性失真;第二部分为线性解混矩阵B，用来补偿混合过程中的线性失真。系统的输出信号y(t)可以定义为

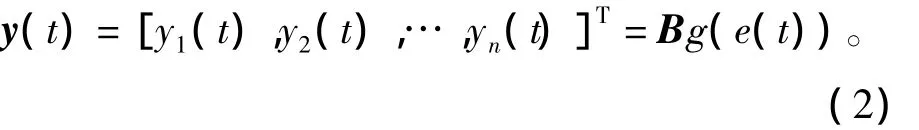
式中，g(·)=f－1(·)，B= ΛMA－1，Λ 为对角矩阵，M为置换矩阵，则非线性解混系统为

后置非线性BSS混合－分离如图1所示。

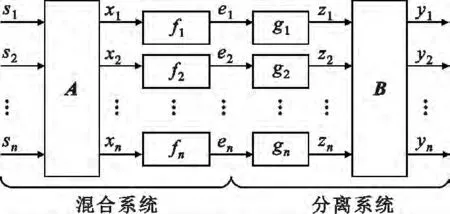
图1 后置非线性BSS混合－分离结构框图Fig.1 Mixing and separating structure diagram of post nonlinear blind source separation

非线性盲源分离算法的关键是根据分离信号y的相互统计独立性来对非线性函数f和矩阵A求逆。

3 维纳系统非线性BSS模型

基于后置非线性BSS的维纳系统将后置非线性BSS的线性混合矩阵A用一个线性滤波器来代替，其信号混合和分离数学模型如图2所示[14－15]，s(t)是信源信号，h()是未知可逆滤波器，f()是未知的可逆无记忆非线性函数，e(t)是观测信号，g()是解混非线性函数，B是解混矩阵，y(t)是对s(t)的估计。

则维纳系统的输出e(t)为

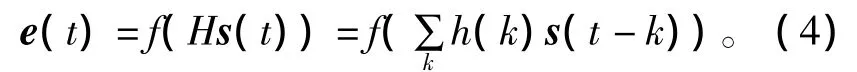
马尔可夫过程是一典型的随机过程，设x(t)是一个随机过程，当过程在时刻t0所处的状态为已知时，时刻t(t＞t0)所处的状态与过程在t0时刻之前的状态无关，这个无后效性的随机过程称为马尔可夫过程。由于后置非线性混合过程中观测信号e(t)是一个瞬时的混合过程，因此也满足马尔可夫过程。本文以最小化互信息作为衡量相互独立的标准，它被定义为

对于q阶马尔可夫模型，条件互信息I可以表示为

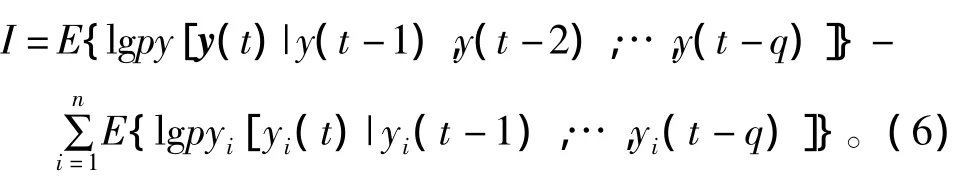
式中，E(·)表示均值。因为概率密度满足

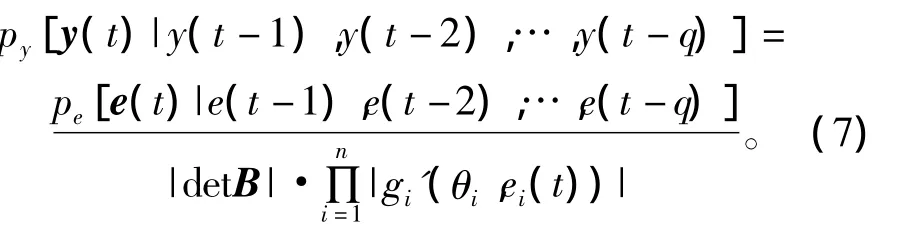
式中，gi'(θi，ei(t))是解混系统中非线性反变换函数对ei(t)的求导，θi是非线性函数gi的调节变量，所以推得[15]

式中，E{lgpe[e(t)|e(t－1)，e(t－2)，…，e(tq)]}不依赖于矩阵B及非线性函数g的参数，所以被省略。目标函数变为

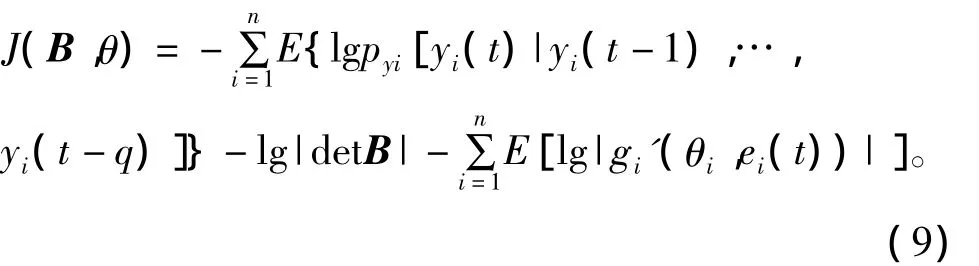
4 基于变步长的维纳系统BSS方法

盲源分离算法的相互统计独立性判据是互信息量传输最小化原则，所以通过对参数B和θ的调整，使输出的信号互信息尽可能小，进而达到最佳的分离效果。采用梯度下降方法对参数进行优化时，算法的性能受步长参数影响较大，大的步长收敛速度比较快，但最小均方误差较大;相反，小的步长收敛速度比较慢，但最小均方误差较小。为了提高算法的收敛性能，本文提出采用基于非线性函数的变步长方法对代价函数进行优化[16]，代价函数梯度较大时使其步长也较大，加快收敛速度;梯度较小时，误差较小接近收敛点，因此使其步长较小，避免收敛振荡，同时也能够减小收敛误差。采用变步长方法对参数B进行更新，其公式为

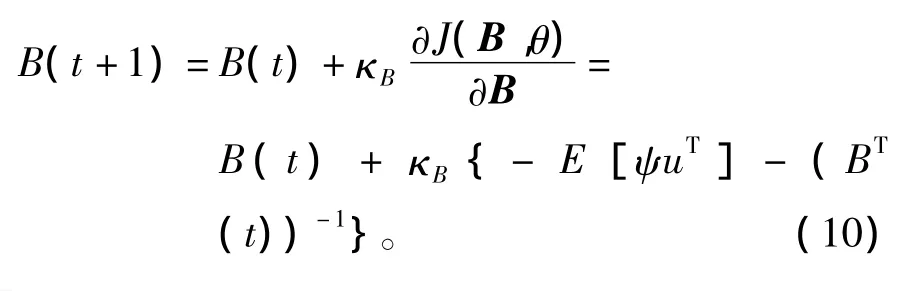
式中，

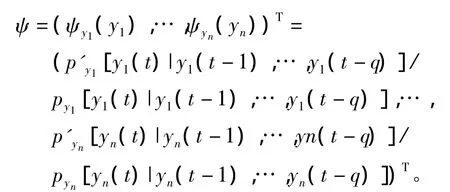
κB(t)如果选取得太大，对分离算法的稳定性会造成很大的影响，根据自适应信号处理中算法的收敛因子应小于输入信号的最大特征值导数的原则，这里取误差阵列第一次迭代时同行元素的绝对值最大元素近似输入信号的特征值，κB(t)的最大值近似为1/2max(|E[ψuT]+BT(t)－1|)。同理，采用变步长优化方法对参数θ进行优化可得

式中，

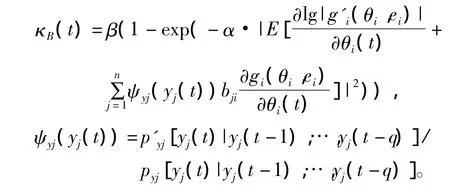
5 MATLAB仿真实验

为了验证本文算法的有效性，选取一个随机信号作为源信号，其波形如图3所示。源信号先后经过一个滤波器(H(z)=1－0.8z－1)得到一个延时信号，延时信号和原始信号作为两个信源信号，经过一个非线性系统(f(x)=x3)后得到两个观测信号，其中非延时观测信号如图4所示，β=0.05，α=3。

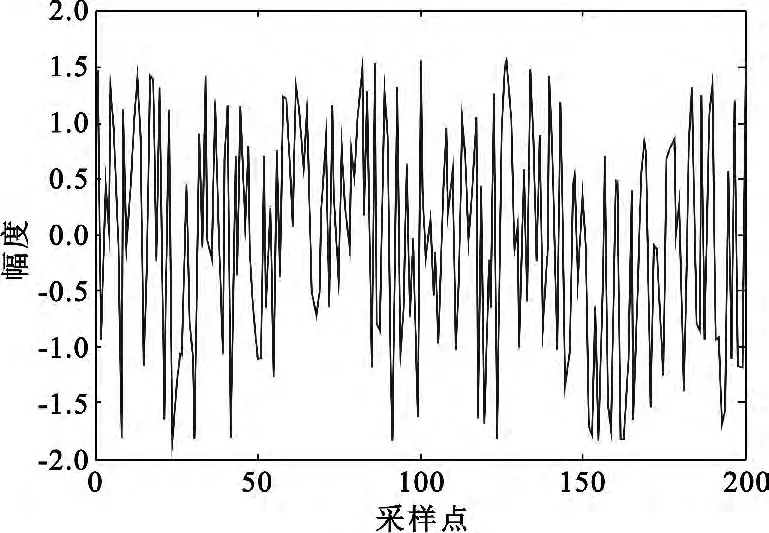
图3 源信号的波形图Fig.3 Waveform of source signal

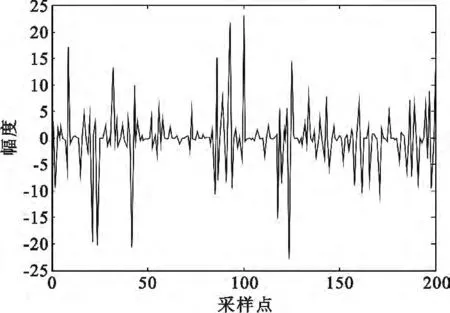
图4 观测信号的波形图Fig.4 Waveform of mixied signal

本文通过变步长算法分离出的信号波形如图5所示。对比图5与图3的波形图可以看出:两信号波形基本一致，说明了该算法很好地分离出了源信号。

图5 分离出的信号波形图Fig.5 Waveform of separated signal

为定量地验证所提算法的性能，用最小均方误差(Minimum Mean Square Error，MMSE)评价分离效果，其值越接近于零，说明算法的分离性能越好。图6是基于非线性函数的变步长算法与文献[15]采用的固定步长算法的MMSE比较图，图中结果是两种算法运行50次得到的平均误差。

图6 最小均方误差性能对比图Fig.6 Performance comparison of minimum mean squared error

由图6可知，固定步长算法分离出源信号需要更新199次左右，而变步长算法只需130次左右，收敛速度明显加快，收敛速度提高了53%。采用固定步长算法收敛时的最小均方误差为1.331 3，而变步长算法的最小均方误差为0.733 5，可见误差性能有很大的改善，误差减少了45%。变步长算法与固定步长算法相比，分离效果有了明显的改善。

6 结论

维纳系统盲源分离算法采用固定点梯度方法对代价函数中的参数进行优化，导致收敛速度和稳态误差矛盾增加。为了解决该问题，提出采用梯度绝对值为变量的非线性变步长方法对非线性盲源分离中的参数进行优化，步长与梯度绝对值的平方成正比，在收敛初期加快了收敛速度，收敛后期减慢收敛速度，避免了振荡误差。相对原算法，该方法总体误差更小，收敛速度更快。对于变步长的最大值范围本文仅给出近似值，还缺少理论推导，今后可对此进行深入研究。

[1]任东晓，叶茂，殷英.基于互信息最小的非线性混合胎儿心电信号提取方法[J].电子测量与仪器学报，2010，24(7):680 －685.REN Dongxiao，YE Mao，YIN Ying.FECG extraction from nonlinear mixture based on minimization of mutual information[J].Journal of electronic measurement and instrument，2010，24(7):680 －685.(in Chinese)

[2]Diamantaras K，Papadimitriou T，Vranou G.Blind separation of multiple binary sources from one nonlinear mixture[C]//Proceedings of 2011 IEEE International Conference on Acoustics，Speech and Signal Processing.Prague:IEEE，2011:2108 －2111.

[3]Almeida M，Almeida L.Nonlinear separation of show through image mixtures using a physical model trained with ICA[J].Signal Processing，2012，29(4):872 －884.

[4]王晓伟，石林锁.自适应非线性BSS及其在齿轮故障诊断中的应用[J].振动与冲击，2012，31(10):45 －48.WANG Xiaowei，SHI Linsuo.Adaptive nonlinear blind source separation and its application in gear faults diagnosis[J].Journal of Vibration and Shock，2012，31(10):45－48.(in Chinese)

[5]Almeida L B.Linear and nonlinear ICA based on mutual information—the MISEP method[J].Signal Processing，2004，84(2):231 －245.

[6]Sun Z L.An extension of MISEP for post－ nonlinearlinear mixture separation[J].IEEE Transactions on Circuits System，2009，56(8):654 －658.

[7]Duarte L T，Jutten C.A mutual information minimization approach for a class of nonlinear recurrent separating systems[C]//Proceedings of 2007 IEEE Workshop on Machine Learning for Signal Processing.Thessaloniki:IEEE，2007:122 －127.

[8]Chen Wei，Li C K，Wai L W，et al.Post－ nonlinear underdetermined ICA by Bayesian statistics[C]//Proceedings of ICA 2006.Charleston，SC，USA:IEEE，2006:773 －780.

[9]Duarte L T，Jutten C，Moussaoui S.A Bayesian Nonlinear Source Separation Method for Smart Ion－Selective Electrode Arrays [J].Sensors Journal，2009，9(12):1763 －1771.

[10]Ren D X，Mao Y S.Extracting post－ nonlinear signal with reference[J].Computers and Electrical Engineering，2011，37(6):1171 －1181.

[11]Ren D X，Mao Y S.Extracting post－ nonlinear signal with specific kurtosis range[J].Applied Mathematics and Computation，2012，218(9):5726 －5738.

[12]Hameling S，Ziehe A，Kawanabe A.Kernel based nonlinear blind source separation[J].Neural Computation，2013(15):1089－1124.

[13]禹华钢，高俊，黄高明.基于批处理和核函数的非线性盲源分离算法[J].电讯技术，2011，51(10):35 －40.YU Huagang，GAO Jun，HUANG Gaoming.Nonlinear blind source separation algorithm based on batch and kernel function[J].Telecommunication Engineering，2011，51(10):35 －40.(in Chinese)

[14]SUN Zhangli，HUANG Deshuan，ZHENG Chunhou，et al.Blind inversion of wiener system for single source using nonlinear blind source separation[C]//Proceedings of 2005 IEEE International Joint Conference on Neural Networks.Killarney，Ireland:IEEE，2005:1235 －1238.

[15]Casals J S，Jutten C.Quasi－ nonprarmetric blind inversion of wiener systems[J].IEEE Transactions on Signal Processing，2001，59(5):917 －924.

[16]高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报，2001，29(8):1094 －1097.GAO Ying，XIE Shengli.A variable step size LMS adaptive filtering algorithm and its analysis[J].ACTA Electronica Sinica，2001，29(8):1094 －1097.(in Chinese)