认知无线电系统中频谱可预测性的递归定量分析*

李红岩

(河南工业大学信息科学与工程学院，郑州450001)

1 引言

认知无线电(Cognitive Radio，CR)系统[1]的可用频谱具有动态性，随着授权用户的用频行为而变化。认知无线电的频谱预测技术对频谱检测的历史数据进行分析，学习授权系统使用频谱的潜在规律，并对未来的频谱占用或空闲情况进行预测。利用频谱预测信息，认知终端和网络进行智能的频谱感知、有选择的频谱接入、主动的频谱切换和动态路由[2－5]，对认知无线电系统的性能稳定有重要作用。

当前有关认知无线电频谱预测的研究多集中在对时隙通信模式下频谱预测机制的探讨，在每个时隙的频谱使用状态(占用或空闲)的检测数据基础上，建立一个二元时间序列，采用ARIMA模型、神经网络模型或马尔可夫链模型对二元时间序列进行预测[6－8]。但是，在时隙观测尺度下获得的时间序列是对频谱状态的微观描述，此时的频谱状态往往具有很大的随机性，这种时间序列是否具有较高的可预测性，目前尚未有文献研究这一问题。

就频谱状态的观测尺度来说，除了时隙这种细粒度外，较粗粒度的观测尺度(如小时)也能提供有效的频谱状态信息。理论上精确的预测方法应该符合授权系统的流量特性，鉴于不同观测尺度下获取的频谱状态信息呈现出完全不同的特征，我们认为有必要按不同尺度采集授权系统的频谱状态数据序列，并分析序列中隐含的频谱使用特性和可预测性，这是建立可靠预测模型的基础。

基于以上分析，本文选取不同观测尺度采集频谱状态时间序列，采用递归图和递归定量分析的方法，从定性和定量两方面对各尺度频谱状态时间序列的可预测性进行分析和比较。

2 递归图和递归定量分析

2.1 递归图

递归图是用来在相空间观测系统状态递归性的工具，它建立在相空间重构的基础上。相空间中在特定时间具有相似特性的状态称为递归状态，递归图的基本原理是将高维相空间中运动轨迹的状态点之间的相似性映射到二维平面上，以可视化的方式直观呈现高维相空间中的递归状态。

设嵌入维数为m，延迟时间为τ，采用延迟坐标法重构相空间，对于给定的时间序列{x(1)，x(2)，…，x(n)}，重构后产生 N个矢量坐标点:xi=(x(i)，x(i+τ)，…，x(i+(m －1)τ))，i=1，…，N。递归图的实现方法是计算一个N×N的矩阵:)

递归图的拓扑和纹理结构能够很好地揭示系统的内在状态，从而可以对系统进行定性分析。其拓扑结构反映了递归图的整体特点，主要包括均匀结构、周期结构、漂移结构以及突变结构等。纹理结构体现递归图的细节特征，主要包括孤立点、对角线、水平线以及垂直线等。

就递归图的图形特点而言，随机系统一般呈现出均匀结构和孤立点，确定型周期性系统表现为重复出现的块状图形结构和较多的平行于主对角线的线段，突然或者急剧变化的动力学系统主要表现为较大的白色区域与较大的块状结构交替出现。

2.2 递归定量分析

在递归图中，若坐标点(i，j)，(i+1，j+1)，…，(i+k，j+k)都是黑点，递归图上将出现一条平行于主对角线的线段。某一时间序列的确定性程度越强，则该序列的递归图中平行于主对角线的线段越长、越多。在时间序列的预测方面，这类线段的存在意味着可以根据状态之间的相似性原理，依据历史状态对未来状态进行预测。根据递归图的递归点密度和沿主对角线方向线段的特征，Zbilut等[9]提出了递归图的定量分析方法，本文选择其中4个特征量作为时间序列可预测性的分析指标。

(1)递归率(Recurrent Rate，RR)

递归点在图中占据的相对数量，表明高维相空间中邻近状态点在所有状态点中所占的比例，其表达式为

(2)确定性(Determinis，DET)

平行于主对角线线段的递归点数与总递归点数的比值，其表达式为

式中，p(l)为长度为l的线段数，lmin一般选择为不小于2的整数。DET越大表明系统的确定性就越强。

(3)熵(Entropy，ENTR)

反映了递归图中主对角线方向线段的频次分布，揭示系统确定性结构的复杂性，熵值越大递归图的确定性结构越复杂。其定义为

(4)平均对角线长度L

主对角线方向线段长度的加权平均值，表示相空间轨迹中互相靠近的两段相轨迹的平均时间长度，L越大系统的确定性越强。其定义为

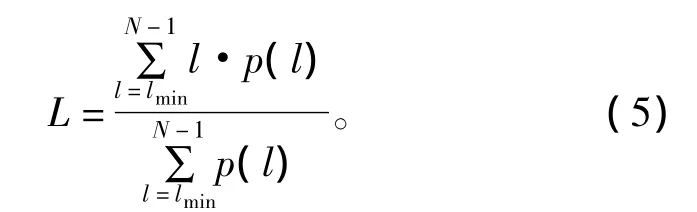
分析以上4个指标的定义，可以看出:RR不能单独反映时间序列的可预测性，因为随机时间序列的RR可能较高，但均表现为孤立的递归点;DET跟RR一起才能表示主对角线方向递归线段的多少，即 M=∑N－1l=lminl·p(l)=DET·RR·N2;平均对角线长度L可以直接作为时间序列的可预测性指标;熵反映了时间序列可预测性的复杂度。

3 频谱可预测性分析

授权系统的频谱利用率普遍较低，以当前应用最为广泛的移动通信系统GSM系统为例，相关研究表明，其下行频点的利用率仅为20%左右，这为认知无线电用户提供了可以进一步利用的频谱机会。下文将以不同观测尺度采集GSM频段的载频状态数据，并分析各种尺度下数据序列的可预测性。

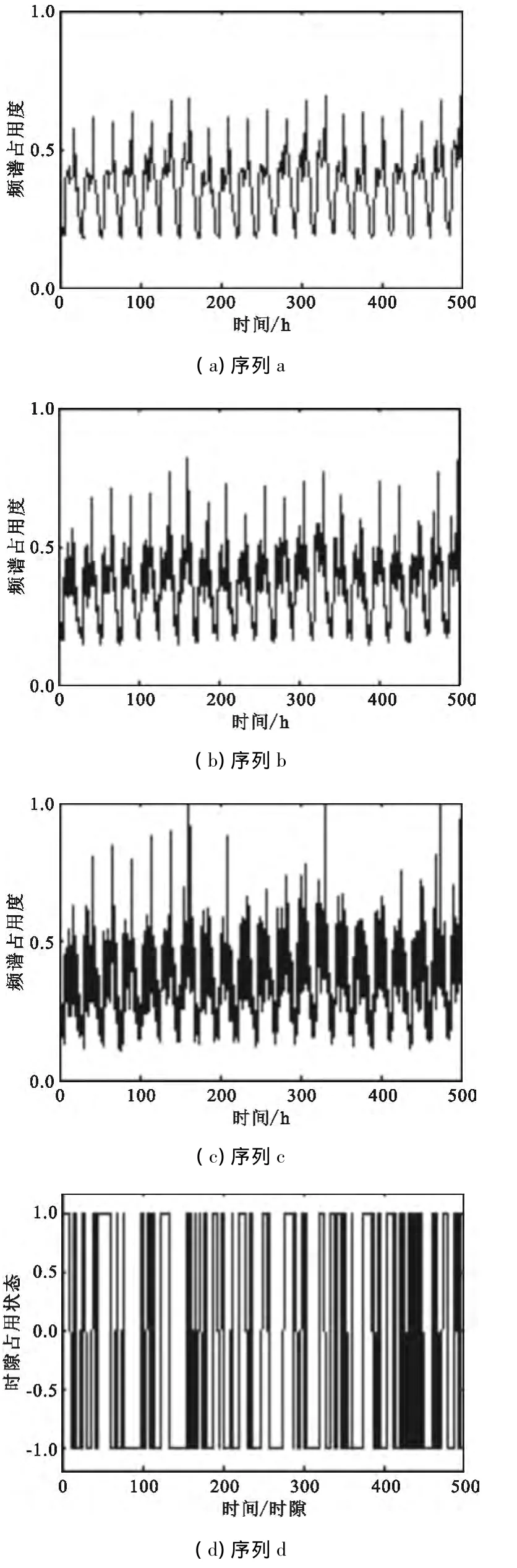
图1 不同观测尺度下的载频状态时间序列Fig.1 Spectrum predictability series under different time scales

3.1 数据采集

实验数据选自我国中部某城市人口密集地区GSM基站子系统的OMC－R操作维护中心，对该中心记录的2013年1月1日～4月30日共120天的原始运维数据进行统计分析，分别取1 h、30 min、15 min为时间间隔，统计每段时间间隔内的频谱占用度，得到3个载频空闲度时间序列，记为序列a、b和c。为分析时隙状态时间序列的可预测性，本文采用计算机仿真的方法模拟GSM信道的通信流量，假定呼叫的到达符合泊松过程，每个用户的通话时长符合负指数分布，信道的流量占用率为50%，模拟得到时隙状态时间序列，记为序列d。序列a～d如图1所示。

观察图1中时间序列的特性，可以直观上看出:当频谱观测尺度较长时，频谱占有率的统计行为表现出较强的确定性和周期或准周期性，在一定的时间范围内呈现缓慢变化的趋势，因而具有较高可预测性。随着观测尺度的缩短，频谱状态时间序列受随机因素影响较大，甚至表现为纯随机行为。如果是纯随机行为，那么在这一时间粒度下频谱是不可预测的，只能用概率论来描述。

3.2 参数选取

由上一节的原理分析可知，阈值选择是影响递归图和递归定量分析的主要参量，阈值太大会使递归图中包含较多的错误递归点;反之，阈值太小将无法合理地呈现递归细节。但是，目前尚未形成一个准则来准确地选取阈值，参照文献[10]，常用的阈值选择办法一是阈值为原始信号标准差的25%左右，二是阈值为相空间直径的10%，三是阈值为信号中可测噪声标准差的5倍。本研究采用第一种方法进行阈值参数的选取，最短主对角线方向线段线段长度lmin取为2。

在时间序列重构参数嵌入维数m和时间延迟τ的选择方面，已有的方法包括虚假最近邻点法、互信息法等，但均缺乏有效的理论支持和广泛的适用性，因此，本文提出一种基于递归定量分析特征量的参数选择办法。具体实现步骤是:首先，假设τ不变，改变m的取值，观察递归图特征量平均对角线长度L的变化，选择使L最大的m值作为嵌入维数;其次，第一步选定的m值固定不变，改变τ的取值，选择使L最大的τ值作为时间延迟参数。参数选择结果见表1。

表1 序列a～d的重构参数列表Table1 Restructure parameters of series a，b，c and d

3.3 递归图分析

图2～5分别显示了序列a～d的递归图变化规律。

图2中递归图整体呈漂移状拓扑结构，沿主对角线平行的方向分布了较多的直线段，但线段的平均长度较短，说明序列a在短时间内具有较强的可预测性。

图2 序列a的递归图Fig.2 Recurrence plots of time series a

观察图3和图4可见:与序列a的递归图相比，序列b和序列c的递归图中包含了较多的纹理细节，这主要是由于序列b和c的重构嵌入维数较低所致。两者在纹理上呈现出周期性的块状结构，这与序列的准周期性是一致的。并且递归图中孤立点较图2多，平行于主对角线的连续线段较少较短，说明与序列a相比，可预测性较差。图3和图4相比，图4中孤立点较多，拓扑结构表现为周期结构和均匀结构的混合体，说明序列c的混沌性和随机性较强，可预测性较弱。

图3 序列b的递归图Fig.3 Recurrence plots of time series b

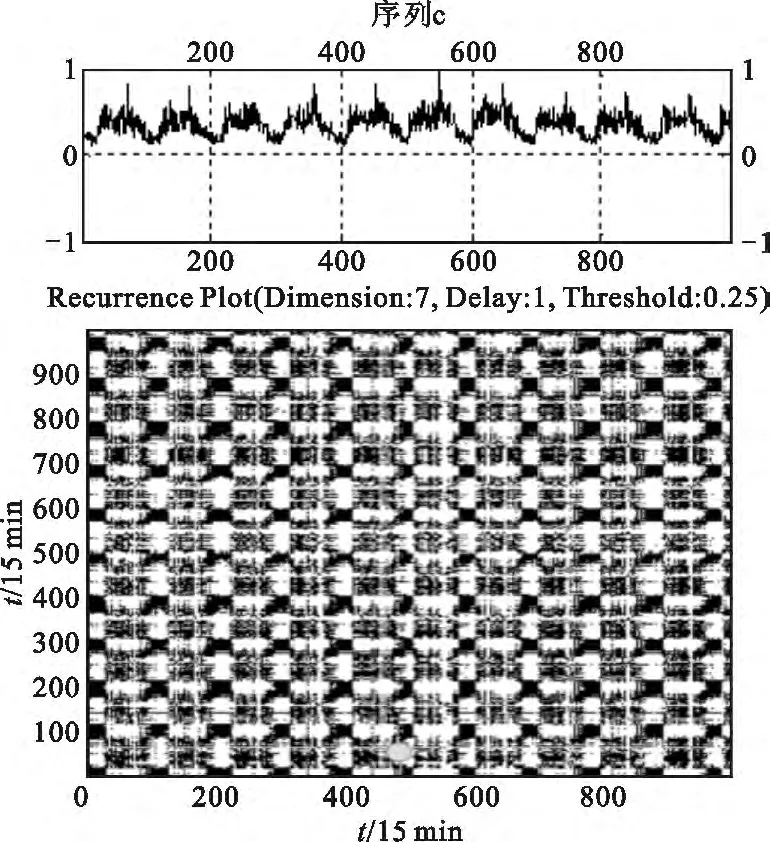
图4 序列c的递归图Fig.4 Recurrence plots of time series c

图5 给出了序列d的递归图图形，其主要拓扑结构为黑白相间的矩形块，表明在矩形块内部的时间阶段系统维持一个相对平稳的状态，对应与时隙状态序列中空闲或占用状态的持续时间。但从整体上看，矩形块的分布不具有明显的规律性，状态的交替是一种随机行为，具有不可预测性。

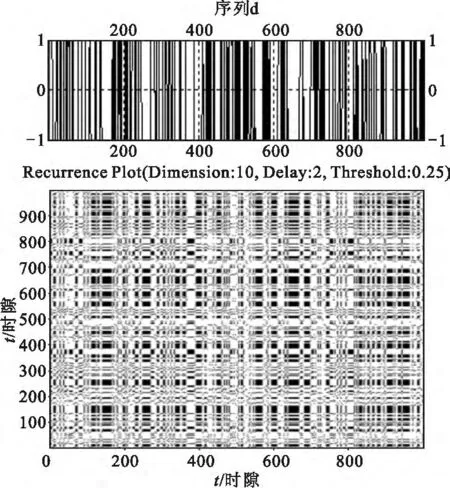
图5 序列d的递归图Fig.5 Recurrence plots of time series d

3.4 递归定量分析

为进一步定量分析序列a～d的可预测性，采用递归定量分析法提取4个特征量:递归率RR、确定度DET、平均对角线长度L和熵ENTR，见表2。

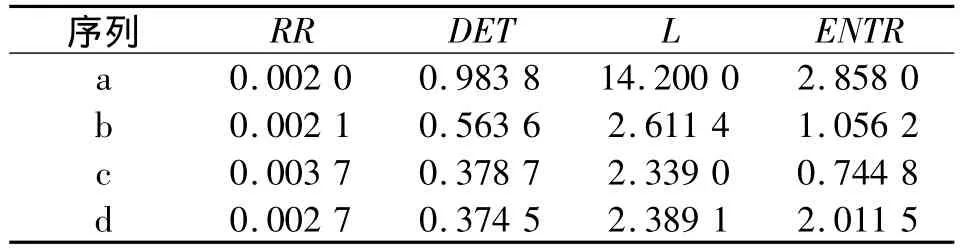
表2 序列a～d可预测性的定量分析指标Table2 Recurrence quantification analysis parameters of series a，b，c and d

由表2数据分析可知，在递归率(RR)近似相等的情况下，序列a～d的确定度指标(DET)有较大差异，其中序列a确定度最大，序列d的确定度最小;指标L也反映出序列a的对角线方向线段的平均长度远远大于其他3个序列，这说明序列序列a的可预测性较高，而且随着观测尺度的降低，频谱状态序列的随机性和混沌性也随之增加，可预测性变差。特征量ENTR显示了4个序列确定性结构的复杂度相差不大。

4 结束语

对频谱的可预测性研究是进行频谱预测的前提，本文通过递归图和递归定量分析，定性和定量研究了基于某GSM基站流量的时间序列可预测性特征。在相空间重构的基础上，对不同观测尺度下的流量数据进行了递归分析。结果表明，随着观测时间尺度的缩小，序列的可预测性变差。其中小时占用度频谱序列表现出较强的周期性和确定性，其混沌性和随机性较弱，因此可选择一般复杂度的预测模型进行预测。而时隙时间序列表现出很强的随机性，可预测性较差，可应用概率论的方法进行分析。对不同观测尺度下频谱状态时间序列进行预测模型的具体构建，是下一步研究的方向。

[1]Haykin S.Cognitive Radio:Brain － empowered Wireless Communications[J].IEEE Journal on Selected Areas in Communications，2005，23(2):201 －220.

[2]Kartlak H.Performance improvement of secondary user transmission in cognitive radio networks[C]//Proceedings of 2012 20th Signal Processing and Communications Applications Conference.Mugla:IEEE，2012:1 －4.

[3]Cacciapuoti A S，Akyildiz I F，Paura L.Primary － user mobility impact on spectrum sensing in Cognitive Radio networks[C]//Proceedings of 2011 IEEE 22nd International Symposium on Personal Indoor and Mobile Radio Communications.Toronto，ON:IEEE，2011:451 －456.

[4]Butun I，Cagatay T A，Altilar D T，et al.Impact of mobility prediction on the performance of Cognitive Radio networks[C]//Proceedings of 2010 Wireless Telecommunications Symposium.Tampa，FL:IEEE，2010:1 －5.

[5]Yong Y，Ngoga S R，Popescu A.Cognitive Radio spectrum decision based on channel usage prediction[C]//Proceedings of the 8th EURO－NGI Conference on Next Generation Internet(NGI).Karlskrona:IEEE，2012:41 －48.

[6]Yarkan S，Arslan H.Binary time series approach to spectrum prediction for cognitive radio[C]//Proceedings of 2007 Proceedings of IEEE 66th Vehicular Technology Conference.Baltimore，MD:IEEE，2007:1563 －1567.

[7]Tumuluru V K，Wang P，Niyato D.A neural network based spectrum prediction scheme for cognitive radio[C]//Proceedings of 2010 IEEE International Conference on Communications.Cape Town:IEEE，2010:1 －5.

[8]Chen Zhe，Guo Nan，Hu Zhen.Experimental Validation of Channel State Prediction Considering Delays in Practical Cognitive Radio[J].IEEE Transactions on Vehicular Technology，2011，60(4):1314 －1325.

[9]Zbilut J P，Webber C L.Recurrence quantification analysis of the logistic equation with transients[J].Physical Letters A，1992，223(4):255 －260.

[10]Schinkel S，Dimigen O，Marwan N.Selection of recurrence threshold for signal detection[J].European Physical Journal－Special Topics，2008，164(1):45 －53.