用于步进频连续波雷达旁瓣抑制的自适应CLEAN技术*
2015-09-28帅晓飞
帅晓飞,詹 旭
(1.中国兵器装备集团(成都)火控技术中心,成都611731;2.四川理工学院自动化与电子信息学院,四川 自贡643000)
1 引言
在步进频连续波(Stepped Frequency Continuous Waveform,SFCW)雷达中,对回波信号通常采用逆快速傅里叶变换(Inverse Fast Fourier Transform,IFFT)技术获得雷达的距离像信息[1],但IFFT固有的高距离旁瓣对邻近弱小目标掩盖问题限制了IFFT在实际中的应用。因此,解决这种掩盖问题以提高雷达对弱小目标的检测性能十分必要。目前,针对该掩盖问题已经取得一定的成果,如Piet van Gendere等人提出的自回归 Yule-Walker算法[2],仿真结果表明该算法在对弱小目标检测和分辨方面优于IFFT技术,但是在发射信号能量较弱时,该算法对旁瓣的抑制能力较差,不能很好地解决弱小目标被掩盖的问题。在文献[3]中,周启荣等人提出了基于熵的旁瓣抑制算法,仿真结果表明最大熵可以有效去除Gibbs振荡造成的拖尾旁瓣,但积分电平较高,最小熵可以降低峰值旁瓣电平和积分旁瓣电平,却会抑制弱信号主瓣幅度。最近,L.Kong等人提出了基于迭代最小均方误差准则(Reiterative Minimum Mean-square Error)的自适应脉压算法(SFCWAPC)[4],仿真和实测数据验证均表明该算法能够有效抑制步进频雷达中的距离像旁瓣,获得更好的检测性能。在文献[5]中,L.Kong等提出了基于迭代最大信干差(Reiterative Maximum Signal Minus Interference Level,RMSMIL)的自适应脉冲压缩算法(SFCW-RMSMIL),仿真实验表明SFCW-RMSMIL比SFCW-APC具有更好的收敛性。然而,在多目标场景中,该算法会严重压制弱小目标的能量,不利于雷达对弱小目标的检测。
基于上述讨论,本文首先对SFCW-RMSMIL算法进行修正,以保证在压制旁瓣的同时准确估计各目标的幅度和位置。经过实验发现,在目标回波信号很弱时,该修正SFCW-RMSMIL算法在场景中目标个数未知的情况下检测性能依然受到限制,且该算法的检测性能对强弱目标所在的相对位置的变化敏感。为此,我们进一步联合修正SFCWRMSMIL 算法和 CLEAN 技术[6-7],充分利用两种算法各自的优点,提出了一种新的自适应CLEAN算法(Adaptive CLEAN,A-CLEAN)。与上述的SFCW-APC和 SFCW -RMSMIL一样,A-CLEAN算法是一种迭代算法。首先,在该算法中用修正SFCW-RMSMIL算法作为前置估计器去取代IFFT;其次,通过比较第k步与第k-1步所有感兴趣距离单元能量之和的大小自适应地判断目标存在与否,在场景中目标数目未知的情况下实现对每一个目标的精确提取。最后,利用仿真数据和实测数据验证了A-CLEAN算法的有效性和实用性。
2 回波模型
假设仿真中感兴趣的距离单元个数为L,那么经过I/Q解调和低通滤波,接收到的回波信号表示如下[5]:

式中,x=[x1,x2,…,xL]T是距离像上 L 个连续采样值,在传统的步进频雷达中,该距离像的获得是通过对回波信号y进行IFFT;(·)H是转置共轭操作;n为噪声向量;信号矩阵S可以按下式进行描述:

式中,f0为起始频率,Δf为步进频率,τl为第 l个距离单元的延时,M为频率步进点数。因此,IFFT估计的目标距离像可以表示为
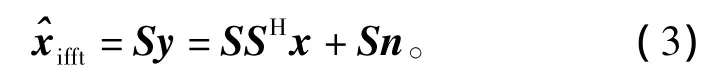
由于IFFT产生的高距离旁瓣会掩盖邻近的小目标,因此在我们过去的工作中也提出了诸多有效的旁瓣抑制算法,而且在单目标场景中和多目标场景中(各目标信噪比变化不大,也即是回波强度接近的场景中),这些算法在旁瓣抑制和对小目标的提取上都取得了良好的效果,不幸的是在各邻近目标信噪比变化很大的多目标场景中,这些算法均不能有效地从旁瓣中提取出小目标,旁瓣抑制性能也随之恶化,这种性能的下降,SFCW-RMSMIL算法表现尤为明显。因此,为了解决SFCW-RMSMIL算法的存在问题,我们首先推导了修正SFCWRMSMIL算法,进而提出了A-CLEAN算法。
3 自适应CLEAN算法(A-CLEAN)
A-CLEAN算法的流程如图1所示。从图中可以看出,该算法主要包含3个模块,第一块是初始化处理,用于找到第一个最大目标,并记录下其幅度与位置;第二块是CLEAN处理,用于提取每一步迭代过程中的最大目标,并自适应地判断目标提取是否完毕;第三块是修正SFCW-RMSMIL估计器,用于在每步迭代过程中,为CLEAN处理提供目标精确的幅度和位置信息。其中,第二块和第三块是算法的关键技术,也是本文的重点。
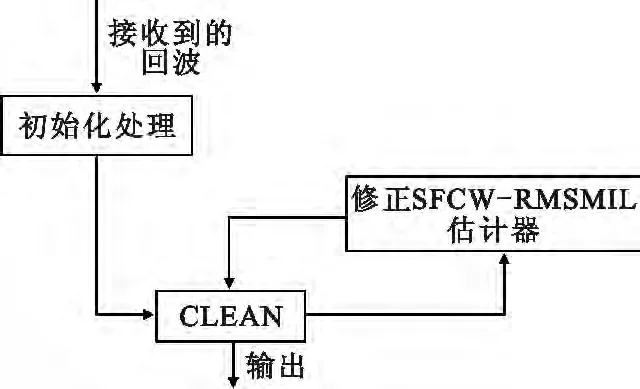
图1 A-CLEAN算法的处理模块Fig.1 Processing modules of A -CLEAN
从文献[5]中可以看出,在修正 SFCW -RMSMIL估计器模块中,其本质就是分别为每个距离单元设计一个基于最大信干差准则的滤波器(MSMIL滤波器),在SFCW-RMSMIL算法中,第l个距离单元的滤波系数可表示为

式中,ρ(l)=|x(l)|2为第l个距离单元的功率估计,这里初始化距离像估计由 IFFT获得;sl=[ej2πf0τl,ej2π(f0+Δf)τl,…,ej2π(f0+(M-1)Δf)τl]H。而修正的SFCW-RMSMIL算法将这里的MSMIL滤波器系数经过归一化,使其满足w(l)sl=1。这个操作减小了强目标对应的权系数幅度,能有效凸显邻近距离单元的弱小目标。假设所有距离单元各项内容相互独立,式(4)中的干扰矩阵C(l)可表示如下:

式中,Rn=σIM为噪声协方差矩阵,这里的σ为噪声功率,IM为M×M维单位矩阵。
传统CLEAN算法是一种迭代算法,并且需要知道场景中的目标个数,根据文献[5-6],第k次迭代过程中该算法的数学等价公式可以表示为

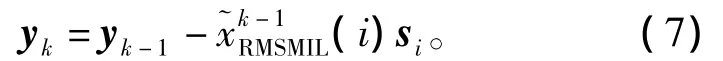
图2展示了A-CLEAN算法的详细流程,其具体步骤也可作如下描述:
(1)当k=1时,对回波y运行式(3)的IFFT获得初始化距离像,找到最大目标所在的位置i=arg{max)},记录其幅度x'i(1)=max),同时计算出所有感兴趣单元的功率之和
(2)在第k步迭代过程中,首先将k-1步得到的估计距离像按式(7)作用于k-1步的回波,进而对残余的回波信号采用修正SFCW-RMSML算法估计其距离像,采用与第1步同样的操作过程记录最大值的幅度和位置,输出第k次迭代的目标距离像Sk,并计算功率总和
(3)如果 Pk<Pk-1,可以确定减掉的最大值是一个真实目标的值,将该目标的位置记录下来,程序跳到 k=k+1 步,重复步骤2,直到 Pk>Pk-1,说明所有目标已经全部被提取出来并令k=K,同时可以给出整个距离历程的目标距离像
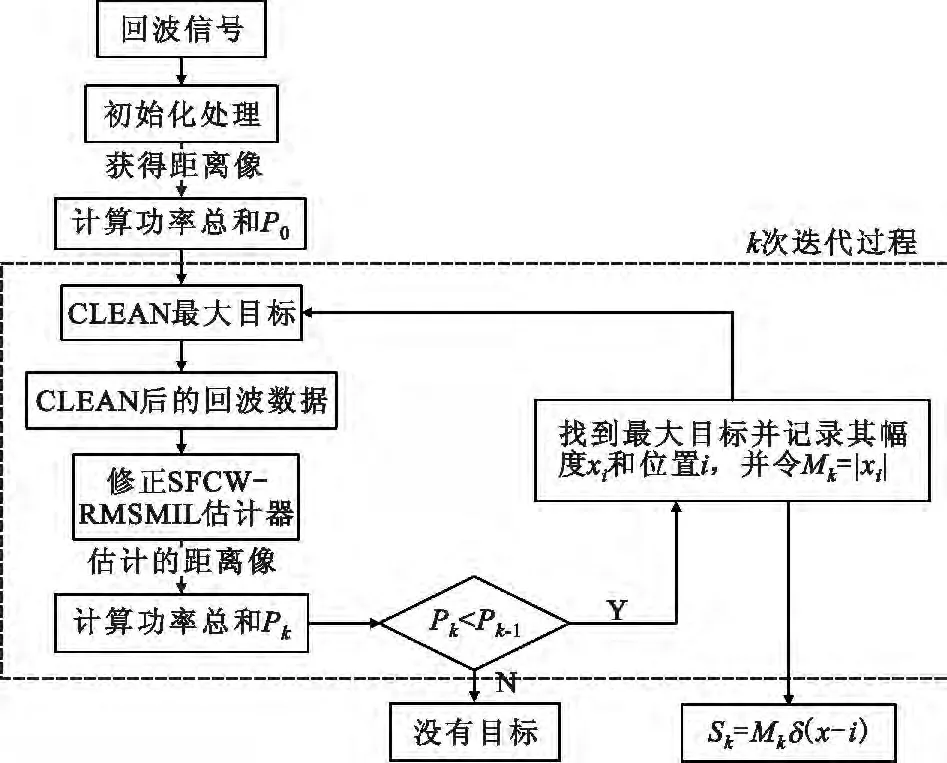
图2 A-CLEAN算法的详细处理流程Fig.2 Detailed processing modules of A -CLEAN algorithm
4 性能评估
本节将通过仿真数据和实测数据来验证ACLEAN算法的有效性,并通过蒙特卡洛仿真实验将A-CLEAN算法和修正SFCW-RMSMIL算法作比较。为了验证算法对弱小目标的发现能力,实验中会在强目标附近放置弱小目标。以下仿真和实测数据的雷达系统参数均按照实验室某步进频连续波雷达设置,如表1所示。

表1 系统参数设置Table1 System parameters
4.1 A-CLEAN算法仿真结果
本实验采用表2所示仿真参数的仿真数据验证修正SFCW-RMSMIL算法和A-CLEAN算法的有效性,从表中可以看出位于距离单元142和155附近有弱小目标。

表2 仿真场景中目标参数设置Table2 Targets parameters for simulation
仿真结果如图3所示,从图3(a)可以看出经过修正SFCW-RMSMIL算法后,在各峰值反映出的目标位置均正确,旁瓣抑制较好,同时不会压制邻近弱小目标的能量。但是当接收到的目标信号很弱时,弱小目标依然有可能淹没在旁瓣中,较难被检测出,同时,在不知道场景中目标个数情况下,被旁瓣掩盖的目标不能有效地被提取出来,因此还需采取措施提高雷达对弱小目标的检测性能。本文进一步采用的A-CLEAN算法,其仿真结果如图3(b)所示。可以看出A-CLEAN算法可以有效地提取场景中的弱小目标(如图3(b)位于第135和第153个距离单元的目标),且该算法在不知道目标个数的情况下依然能够精确地提取出场景中的每一个目标。

图3 两种算法仿真结果Fig.3 Simulation results of modified SFCW -RMSMIL and A-CLEAN
4.2 检测性能分析实验
本实验通过蒙特卡洛实验分析修正SFCWRMSMIL算法与A-CLEAN算法的性能。实验中采用恒虚警检测器,虚警概率为10-2,门限用10 000次试验数据求得,发现概率由3000次试验求得。该实验场景中首先固定强目标的位置和其散射强度,这里设其位于第15个距离单元,信噪比为50 dB,强目标与弱小目标的信噪比差值如图4横坐标所示在30~70 dB变化,我们给出了对两个不同位置弱小目标的检测性能曲线,L=5和L=8分别表示弱小目标在远离雷达方向与强目标的绝对位置相差5个和8个距离单元。从图中可以看出:其一,采用 ACLEAN算法,雷达对弱小目标的性能要优于采用修正 SFCW -RMSMIL算法;其二,修正 SFCW -RMSMIL算法的检测性能对目标的位置变化敏感,但是A-CLEAN算法受目标所在位置的影响很小,检测性能的稳定性优于修正SFCW-RMSMIL算法;其三,随着两目标信噪比差值的增加,弱小目标的检测性能逐渐降低。

图4 两种算法通过蒙特卡洛仿真结果Fig.4 Detection probability of modified SFCW -RMSMIL and A-CLEAN
4.3 实测数据验证
为了验证A-CLEAN算法的实用性,本小节采用实测数据进行验证。场景中我们放置3个材质相同大小不同的球体目标于第90、123、151个距离单元,图5给出了两种算法的处理结果。从图5(a)可以看出,3个目标间信噪比差值较大,位于第123个距离单元的目标甚至已经被掩盖在旁瓣或是噪声基底中。而从图5(b)中的A-CLEAN处理结果可以明显看出,该目标被有效地提取出来,场景中共有3个目标,而经过A-CLEAN算法,也能自适应地准确地提取出3个目标。

图5 实测数据验证结果Fig.5 Numerical results of real data
5 结束语
我们针对在多目标场景中强目标距离旁瓣掩盖附近弱小目标问题,提出了基于CLEAN技术的有效检测弱小目标的A-CLEAN算法。该算法联合修正的SFCW-RMSMIL算法与CLEAN技术,不但能提高弱小目标的发现能力,还能精确估计目标的位置和幅度。通过仿真实验和实测数据,进一步验证了A-CLEAN算法的有效性。由于该算法利用多次迭代逐次去除强目标对邻近目标的影响,计算量比较大,这对工程应用的硬件要求较高,优化该算法减小计算量将是我们下一步的研究内容。
[1]Van Genderen P,Nicolaescu I.System description of a stepped frequency CW radar for humanitarian demining[C]//Proceedings of 2nd International Workshop on Advanced Ground Penetrating Radar.Delft,Netherlands:IEEE,2003:9 -15.
[2]Van Genderen P,Nicolaescu I.Imaging of stepped frequency continuous wave GPR data using the Yule-Walker parametric method[C]//Proceedings of 2005 Radar Conference.Paris:IEEE,2005:77 -80.
[3]周启荣,黄春琳,陆珉.基于熵步进频率探地雷达距离旁瓣抑制[J].雷达科学与技术,2008,6(5):361 -365.ZHOU Qirong,HUANG Chunlin,LU Min.Range side -lobe suppression based on Entropy in stepped-fequency ground penetrating radar[J].Radar Science and Technology,2008,6(5):361 -365.(in Chinese)
[4]Kong L J,Zhao B,Cui G L.Sidelobe suppression method for stepped frequency continuous- wave radar[J].Electronisc Letters,2011,47(7):460 -462.
[5]Yang M,Kong L J,Zhao B.A novel method to suppress range sidelobes for stepped frequency continuous-wave radar[C]//Proceedings of 2012 IEEE Radar Conference.Atlanta,GA:IEEE,2012:404 -407.
[6]Abramovich Y I.Compensation methods of resolution of wideband signals[J].Radio Engineering and Electronics Physics,1978,23(1):54 -59.
[7]Deng Hai.Effective CLEAN algorithms for performance - enhanced detection of binary coding radar signals[J].IEEE Transactions on Signal Processing,2004,52(1):72 -78.
