动态几何问题的分类探析
2015-09-28福建省连城冠豸中学李永忠
福建省连城冠豸中学 李永忠
近年来,经过对中考试题的研究,我们发现动态几何问题作为一个命题的热点在各地中考题中频繁出现,题型灵活多变,常以点、线、面运动为载体,探求函数关系及存在性等方面的问题,从形式上看,可分为点动、线动和形动三种类型,这类问题主要以几何图形为背景,运动变化为主线,集多个知识点为一体,集多种解题思想于一题,这类题综合性较强,对学生能力要求高,它能全面考查学生的实践操作能力、空间想象能力以及分析问题和解决问题的能力.现以部分中考题为例,分类探析动态几何问题的命题方法和解题思路.
一、点动型
在几何图形的背景下,以点动为载体的问题主要分为两类,即单动点问题和双动点问题,其中单动点问题一般涉及到一次函数或反比例函数,双动点问题一般涉及到二次函数,这两类都可和存在性问题联系;所给问题又常与函数图像、最值及存在性问题紧密相关.
例1 如图,四边形ABCD是边长为2cm的正方形,动点P在ABCD的边上沿A→B→C→D的路径以1cm/s的速度运动,在这个运动过程中,△APD的面积S(cm2)随时间 t(s)的变化关系用图像表示,正确的是( )
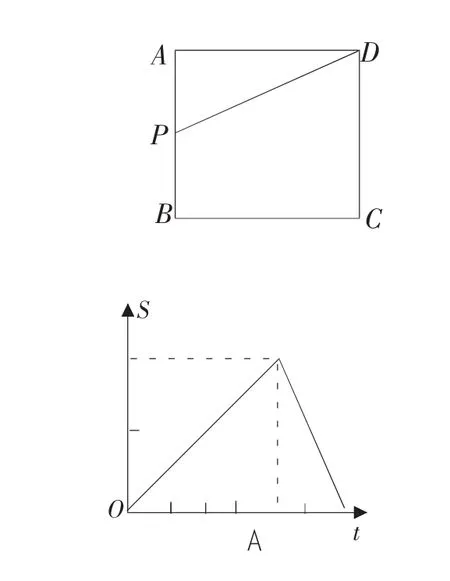
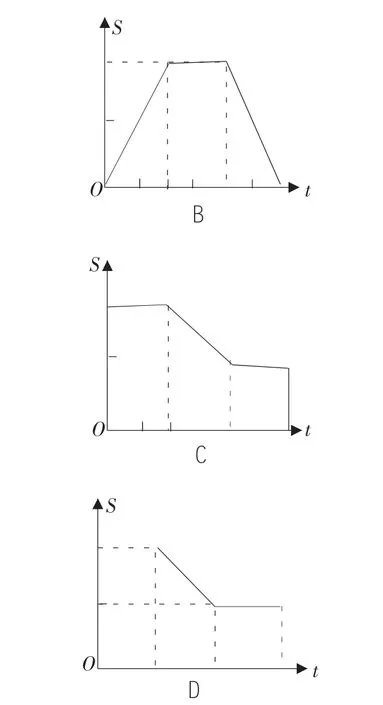
简析:本题将点的运动过程中形成的函数解析式与其相应的函数图像有机结合在一起,二者相辅相成,突出数形结合、分类讨论、函数建模在解题中的灵活运用.解题的关键是自变量t取值范围的分类讨论及在各个范围内面积S与时间t的函数关系式.
例2 如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(3,0),(3,4),动点 M、N 分别同时从点O、B同时出发,以每秒1个单位的速度运动,其中点M沿OA向终点A移动,点N沿BC向终点C运动,过点N作NP⊥x轴,交AC于点P,连接MP,已知动点运动了x秒.
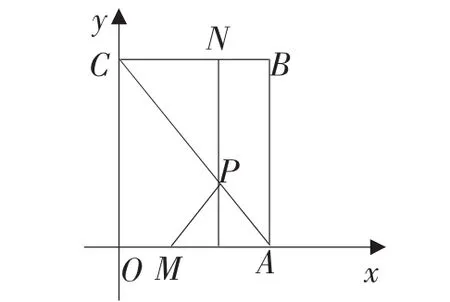
(1)点P的坐标为( , )(用含x的代数式表示);
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.
简析:本题是以双点运动构建的集函数、最值问题、存在性问题为一体的综合题.包含着相似三角形、勾股定理和二次函数等知识的综合运用.题(1)是关键,为下面问题的解决分散了难点,起到点拨作用;题(2)是以矩形为背景创设的函数最值问题,在知识点上侧重对二次函数关系和最值问题的考查,要求学生有扎实的基础知识、灵活的解题方法、良好的思维品质,解题的关键在于应用上小题的结论确定点P到OA的距离;题(3)是存在性问题,要求学生能按照等腰三角形的定义进行分类.探究此类问题要在“动”中取“静”,分情况画出动点在特定位置的图形,并要充分应用数形结合、转化化归和分类讨论等数学思想,解题的关键在于通过相似、勾股定理、等腰三角形性质等知识点按分类的情况列出相应的方程给予解决.
二、线动型
线动形动态几何问题常见于在坐标平面下,通过直线与原定的几何图形(常以矩形、梯形为主)的相对移动,从而构造出在各种范围内不同图形而设置的问题,解决此类问题要善于借助动态思维,应用分类的数学思想,从变中求不变,抓住静的瞬间,把动态问题转化为静态问题解决.
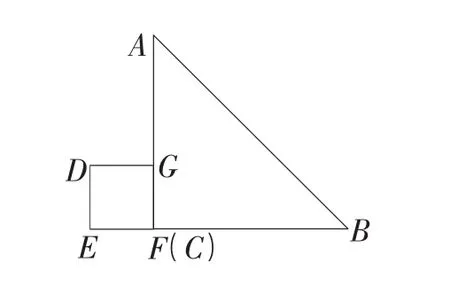
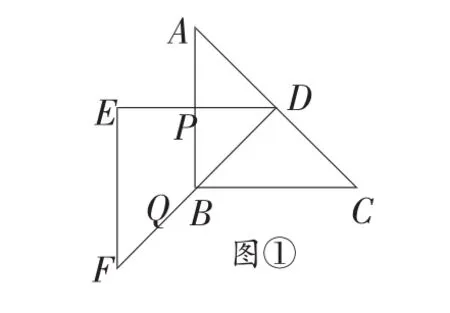
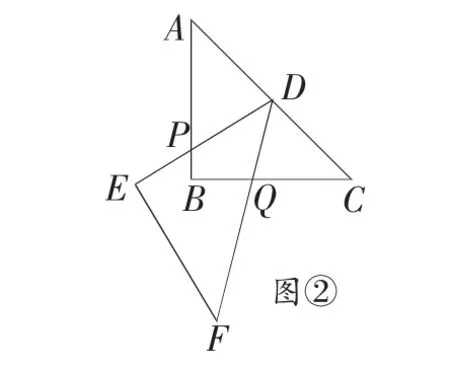
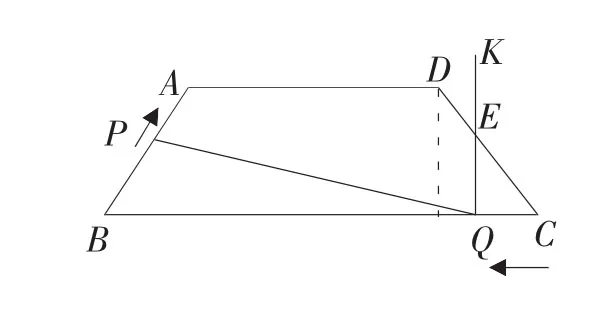
例3 如图,直线CD:y=2x+1与边长为1的正方形OABC交于点C,与x轴交于点D.将直线CD沿x轴正方向平移m个单位(0 简析:由于直线在平移过程中位置的不同,截正方形所得图形也不同,因此应分类讨论求解.解题的关键是明确按什么分类标准,分哪几类,难点在于抓住临界位置,结合所给自变量m范围进行精心合理分类,并进行分类画图,逐个求解. 例4 如图,在等腰梯形ABCD中,AD∥BC,AB=DC=50,AD=75,BC=135.点P从点B出发沿折线段BA-AD-DC以每秒5个单位长度的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长度的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E.点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止.设点P运动的时间是t秒(t>0). (1)当点P到达终点C时,求t的值.并指出此时BQ的长; (2)当点P运动到AD上时,t何值能使四边形PQCD为平行四边形; (3)设射线QK扫过梯形ABCD的面积为S,分别求出点E运动到CD、DA上时,S与t的函数关系式,(不必写出t的取值范围) 简析:本题为梯形背景下的动态几何问题.其中既涉及到双动点问题也涉及到直线运动问题,题目条件较多,对学生的分析问题能力要求较高,尤其是第 (3)小题,解题时容易受到动点P的影响,解决这小题要用到勾股定理、相似三角形及梯形相关知识,解题的关键在于充分利用Rt△DFC这一隐含的已知条件,分类画出相应图形解决. 形动类动态几何问题指在平面内两个几何图形之间的问题,一般情况下,其中一个位置固定,另一个图形相对于位置固定的图形作图形变换(含平移、旋转、轴对称等),通过图形变换,探求各种不同位置下的函数关系问题,此类问题一般以压轴题为主,探讨在连续变换的条件下隐含着的不变性质,此类问题的特点在于常常利用相似三角形的性质、勾股定理、图形的面积关系、特殊几何图形的几何性质,以方程为纽带获得函数关系式,从而达到解题目的. 例5 如图,在△ABC中,∠ACB=90°,AC=BC=6cm,正方形 DEFG 的边长为2cm,其一边EF在直线BC上,开始时点F与点C重合,让正方形DEFG沿直线CB向右以每秒1cm的速度作匀速运动,最后点E与点B重合. (1)请直接写出该正方形运动6秒时与△ABC重叠部分面积的大小; (2)设运动时间为x(秒),运动过程中正方形DEFG与△ABC重叠部分的面积为y(cm2). ①在该正方形运动6秒后至运动停止前这段时间内,求y与x之间的函数关系式. ②在该正方形整个运动过程中, 求当x为何值时,y=0.5. 简析:本题属形动中平移问题,常见的题型是通过图形的移动求两个图形重叠部分的面积与运动时间之间的函数关系式,也常与最值问题、特殊时刻的面积或时间的值相关;解题的关键在于确定图形移动过程的临界位置,并把所给自变量进行合理分类,确定自变量取值范围.此类问题一般要结合方程、相似、勾股定理等相关知识并进行综合应用. 例6 把两块全等的含45°角的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,AB=DE.把三角板 ABC 固定不动,让三角板DEF绕点O旋转,设直线DE与射线AB相交于点P,射线DF与线段BC相交于点Q. (1)如图①,当射线DF经过点B时,易证△APD∽△CDQ.此时,AP·CQ= . (2)将三角板DEF由图①位置绕O点沿逆时针方向旋转 α 角(0°<а<90°),问AP·CQ的值是否改变?并说明理由. (3)在(2)的条件下,设 CQ=x,两块三角板重叠部分的面积为y,求y与x的函数关系式.(图②③供解题用) 简析:本题属形动中的旋转类问题,这种用两个全等图形构造的问题,用全等或相似的知识证明图中的存在的不变的量是其题目的特点.如本题的三个图形中,均有△APD∽△CDQ,从而AP·CQ的值为定值.题目的设计一般由简到难,呈“步步高”的趋势,解题的关键在于抓住题中的定量,以不动制动,通过观察、探索、比较等方法解决.本题第(3)小题难度较大,既要用到前面的结论,又要用到相似的知识,解题的关键在于利用点D到两直角边距离为隐含条件,通过相似的方法处理,从而解决线段MQ与x的关系. 通过以上分析,可以清楚的发现,动态几何问题的设置往往带有操作性、探索性和开放性,问题的解决需要通过操作、实验、观察、猜测、探索、验证等一系列的数学活动,渗透数形结合、转化化归、函数方程、分类讨论等数学思想,内容丰富、解法灵活,具有开放性,建议在教学中,加强对此类问题的分析,必将对培养学生的动手能力、空间观念和几何变换思想有较大的帮助.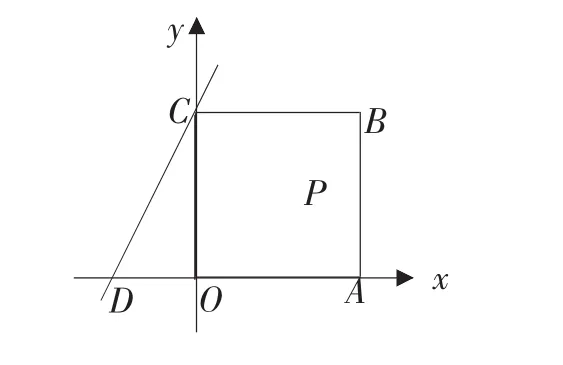
三、形动型