基于自抗扰控制原理的MMC-HVDC控制策略

刘 炜，王朝亮，赵成勇，郭春义，黄晓明，陆 翌，裘 鹏

（1.华北电力大学 新能源电力系统国家重点实验室，北京 102206；2.国网浙江省电力公司电力科学研究院，浙江 杭州 310014）

0 引言

由德国慕尼黑联邦国防军大学提出的模块化多电平换流器MMC（Modular Multilevel Converter）拓扑结构[1]，因为具有模块化程度高、开关损耗低、输出波形谐波含量少、适用于高电压大功率场合等优点[2]，得到了国内外学术界的广泛关注[3-8]。 文献[9-11]对 MMC 的拓扑结构、子模块 SM（Sub-Module）电容电压均衡控制、环流抑制、调制策略及控制策略等进行了研究。传统的MMC-HVDC控制策略都是基于连续时间状态空间下的MMC-HVDC数学模型，而实际的控制器通常采用计算机控制，其本质为采样控制。因此文献[12]建立了MMC离散化数学模型，并在此基础上设计了MMC电流内环离散控制器。但是MMC-HVDC系统是一非线性强耦合系统，所建立的离散化数学模型并不能精确描述系统的状态特性，加之采用环节的延时作用，系统的抗扰性能并不理想。自抗扰控制ADRC（Auto Disturbance Rejection Control）理论[13]吸收了现代控制理论的成果，发扬并丰富了PID思想的精髓，利用扩张状态观测器（ESO）对系统内外扰动进行估计补偿，具有较强的抗扰性能。文献[14]将ADRC技术应用于三相电压型PWM整流器，获得了很好的控制效果。

本文基于ADRC理论，对传统ADRC控制器的非线性函数提出了改进，在此基础上设计了MMCHVDC外环控制器，以改善采用电流内环离散控制器后带来的抗扰性能下降的问题；针对MMC存在的环流问题设计了基于ADRC技术的直接环流抑制器CCSC（Circulating Current Suppressing Controller）；在电网电压不平衡条件下，设计了基于ADRC控制器的负序电流抑制器。最后在PSCAD/EMTDC环境仿真验证了所设计控制器的有效性。

1 MMC的基本原理

1.1 基本结构

三相n+1电平MMC基本结构如图1（a）所示，MMC的每个桥臂由n个子模块和1个电抗器L0串联组成，上、下2个桥臂组成1个相单元。

目前MMC-HVDC工程主要采用半桥子模块拓扑结构。半桥子模块结构如图1（b）所示，其由2个IGBT（VT1、VT2）、2 个反向二极管（VD1、VD2）以及 1 个直流电容器C组成。正常运行时子模块工作状态如表1所示，其中S代表子模块状态，S=1代表子模块投入，S=0代表子模块切除，USM为输出电压。

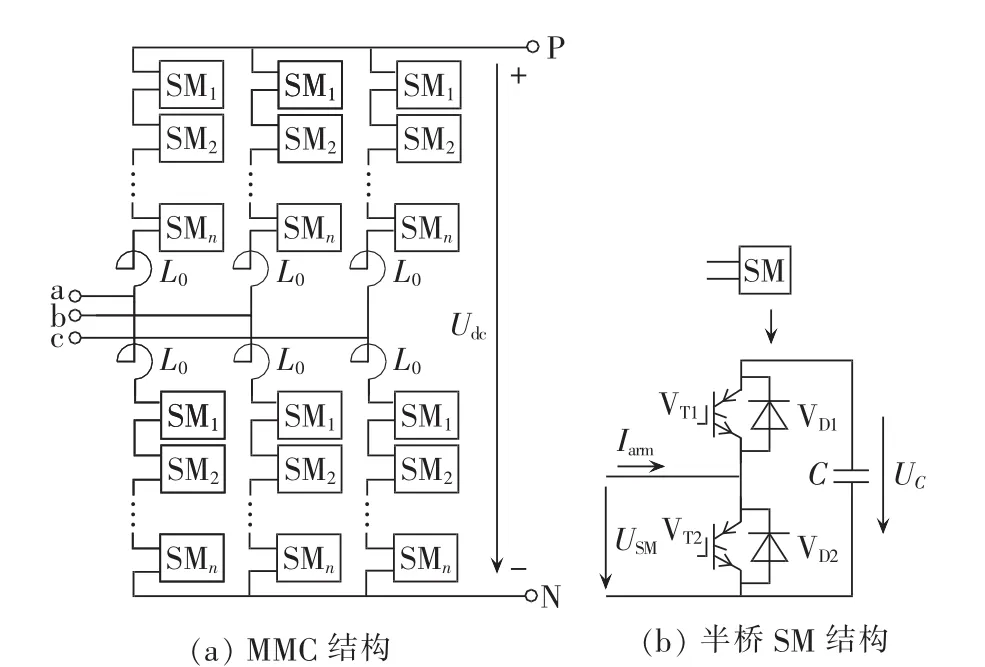
图1 MMC拓扑结构Fig.1 Topological structure of MMC

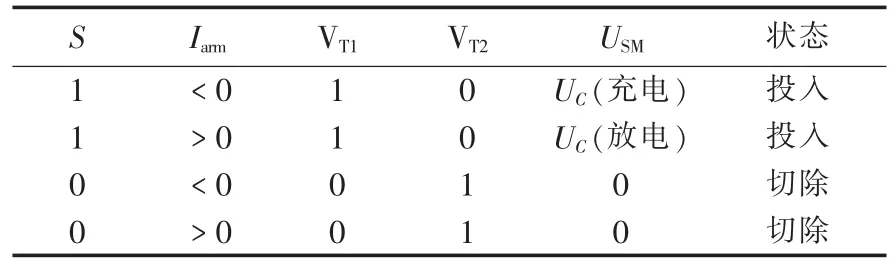
表1 子模块的工作状态Table 1 Working states of sub-module

1.2 数学模型

图2为 MMC 单相等值电路，其中 usk（k=a，b，c）、R、R0分别为交流系统的等值电源、等值电阻及桥臂电感和换流器损耗共同的等效电阻；LT、L0分别为变压器等效漏感和桥臂电感；upk、unk分别为MMC的上、下桥臂电压；ipk、ink分别为上、下桥臂电流；下标中p代表上桥臂，n代表下桥臂。

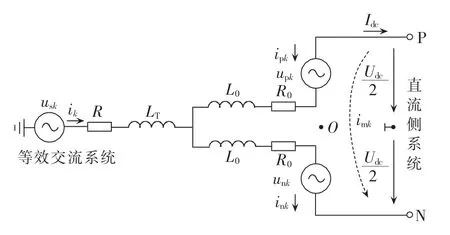
图2 MMC-HVDC系统整流侧单相等值电路Fig.2 Rectifier-side single-phase equivalent circuit of MMC-HVDC system

根据图2所示MMC的电路结构，可得MMC交流侧数学模型和内部电压、电流特性方程[15]：

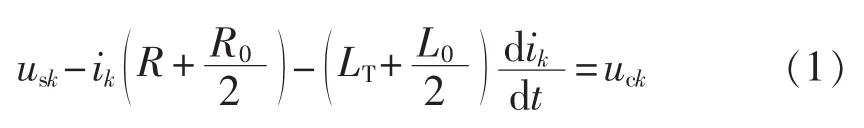
其中，ik为交流侧电流；uck定义为虚拟点O的电动势，即换流器出口等效电压，可表示为式（2）。

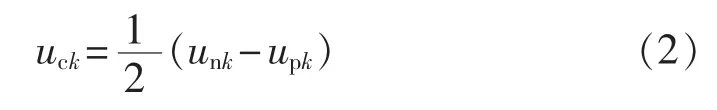
由上式可知通过控制MMC各相上、下桥臂电压upk、unk可实现对换流器出口电压的等效控制，进而可控制MMC与交流系统之间的功率交换。

2 MMC-HVDC电流内环控制器设计

系统稳态运行时，由于R0数值上很小而可忽略，对式（1）简化后进行派克变换得到dq同步旋转坐标下的MMC交流侧数学模型：

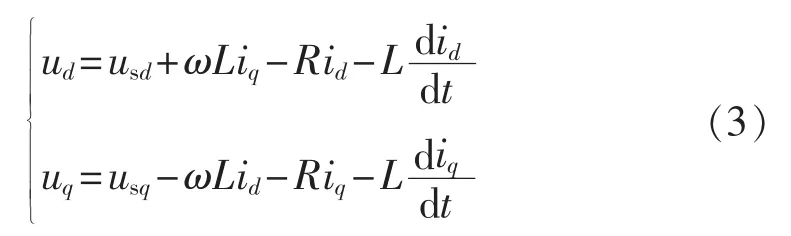
其中，L=LT+L0/2；usd、usq、id、iq分别为交流系统三相电压与电流的d、q轴分量；ud、uq分别为 MMC出口等效电压的d、q轴分量。设控制器的采样周期为Ts，并将式（3）离散化为：

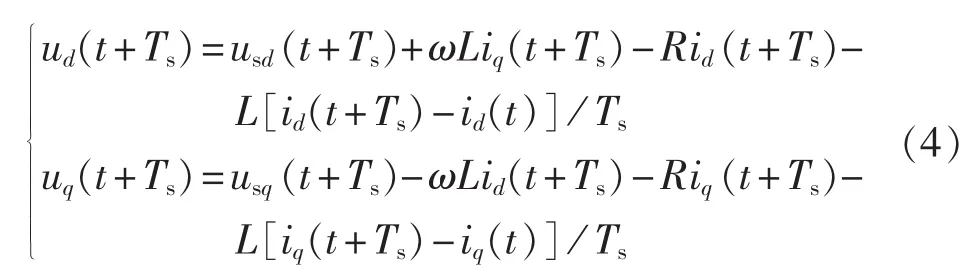
考虑到MMC开关频率远高于交流系统基频且控制指令计算需要一定的时间，可认为在一个采样周期Ts内各物理量基本保持不变，则式（4）可表示为：

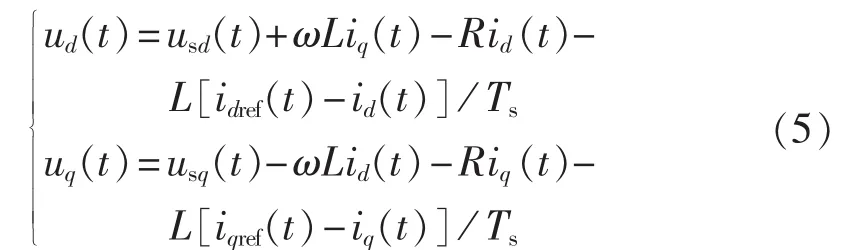
其中，idref、iqref为MMC电流内环输入参考值。

根据式（5）设计MMC电流内环离散控制器如图3所示。

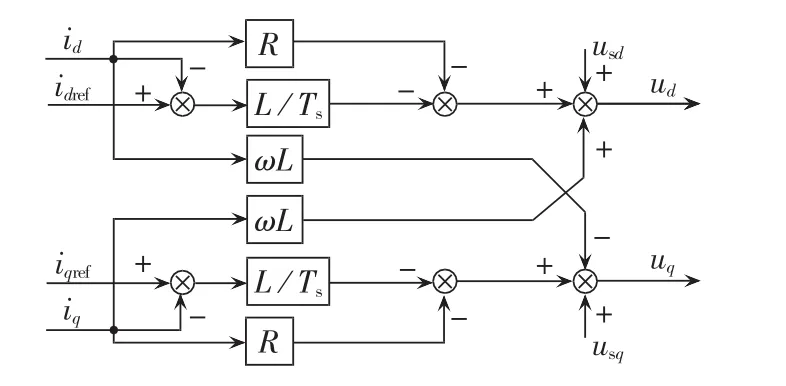
图3 MMC电流内环离散控制器Fig.3 Inner-loop discrete current controller of MMC

3 MMC-HVDC的ADRC

3.1 ADRC基本原理

本文采用的一阶ADRC控制器如图4所示，其主要由三部分组成：跟踪微分器（TD）、扩张状态观测器和非线性状态误差反馈（NLSEF）。

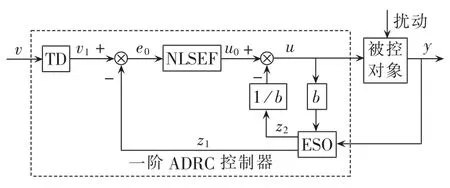
图4 一阶ADRC控制器原理图Fig.4 Schematic diagram of first-order ADRC

3.1.1 跟踪微分器

跟踪微分器能够合理提取微分信号并根据被控对象的承受能力合理安排过渡过程，从而有效协调系统输出的快速性与超调之间的矛盾。

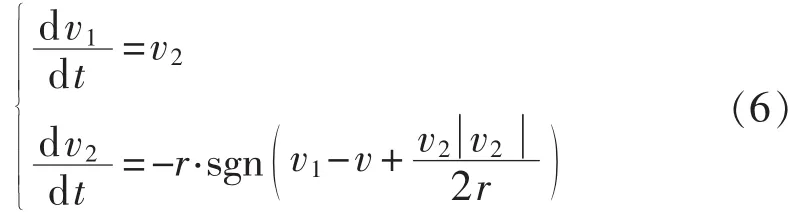
其中，v为输入的参考信号；v1、v2分别为输入信号v的跟踪信号与广义微分信号；r为调整参数，r值越大，跟踪微分器的跟踪能力越强。

3.1.2 扩张状态观测器

扩张状态观测器是ADRC控制器的核心部分，其将系统未建模的部分和未知的内部和外部扰动归结为系统的总扰动，通过扩张一维的方法，实时估计并动态补偿系统的扰动，使系统线性化为积分器串联结构，从而简化了控制对象，提高了控制品质。二阶扩张状态观测器可表示为∶

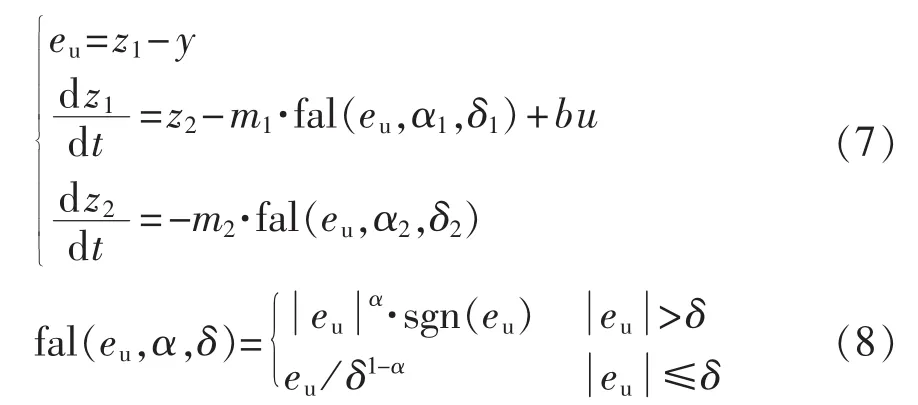
其中，eu为扰动观测器输出信号z1与系统输出信号y的误差信号；α 为可调参数（0＜α＜1）；δ为滤波因子；y为系统输出值；b为补偿因子；m1、m2为输出误差校正系数；fal为非线性状态误差反馈函数，是扩张状态观测器的核心部分；z1、z2分别为系统输出和系统扰动的估计值。

3.1.3 非线性状态误差反馈

非线性状态误差反馈利用非线性结构抑制系统误差，改善了系统的控制品质。ADRC控制器中的非线性状态误差反馈可表示为：

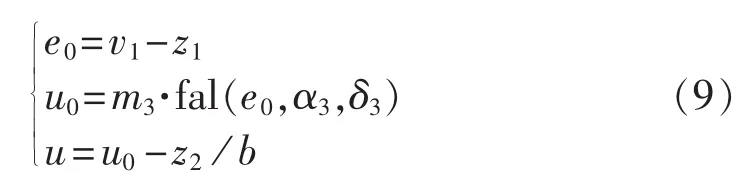
其中，e0为跟踪信号v1与扰动观测器输出信号z1的误差信号；u为控制器的输出；u0为未经扩张观测器动态补偿的控制器输出；m3为比例系数，可影响系统电压及功率的逼近程度。

3.2 MMC外环ADRC控制器设计

MMC传统的PQ解耦双闭环控制器中，外环控制器的输出作为内环控制器的输入参考值，其控制性能决定着整个MMC系统的控制品质，而MMC结构较为复杂，如图1中所示MMC拓扑中6个桥臂电流以及6n个子模块电容的电压均为状态变量，当MMC电平数很高时，其精确的状态方程难以实现。ADRC控制器将作用于被控对象的所有不确定因素作用都归结为“未知扰动”，而用对象的输入、输出数据对其进行估计补偿，其对受控对象的数学模型依赖性不强，具有较快的响应速度、良好的控制精度以及很强的鲁棒性，因此本文将基于ADRC理论设计MMC外环控制器。

传统ADRC控制器中的非线性函数式（8）由于在±δ处非光滑而存在的控制力抖动问题，文献[16]对此提出了一种新型非线性函数fatg（x，α）。但其在大误差情形下增益较大，易造成控制作用饱和，控制性能不如 fal（x，α，δ），因此本文在此基础上对其进行改进，引入非线性函数fel，如式（10）所示，当控制系统的输入x较大时具有较小的增益，可以有效降低控制系统发生控制输入过饱和现象的概率。3种非线性函数的对比如图5所示。可以看出，fel与fatg在x=±δ处光滑，而fal在x=±δ处非光滑。

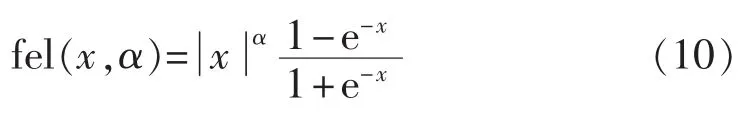
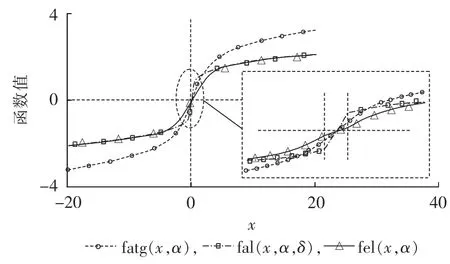
图5 3种非线性函数的比较Fig.5 Comparison among three nonlinear functions

MMC正常运行时外环控制器一端采用定直流电压控制并配合无功功率控制，另一端采用定有功功率控制和无功功率控制。对于外环电压控制器，即定直流电压与定交流电压控制器，根据式（6）—（10）可以设计出相应的ADRC外环控制器，如图6中的（a）、（b）所示。 对于外环功率控制器，系统正常运行时在所选的 dq坐标下，usd=us，usq=0，MMC 与交流系统之间交换的功率可为：

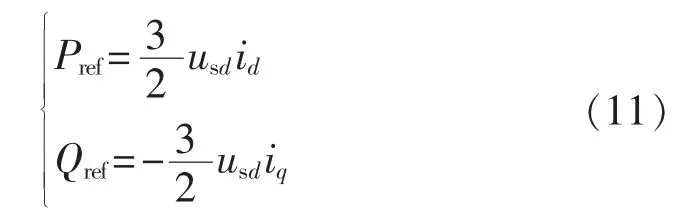
根据式（11）可得：

将式（12）中的id、iq作为系统的已知扰动项加入ADRC 控制器中。 图6（c）、（d）分别为 MMC 定有功功率、定无功功率ADRC控制器原理框图。

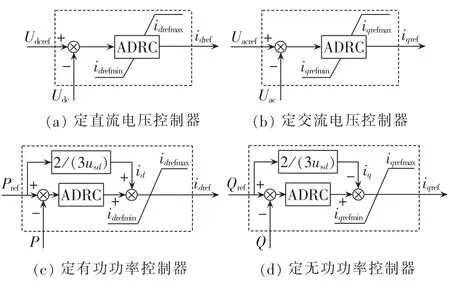
图6 外环电压控制器和功率控制器Fig.6 Outer-loop voltage controller and power controller

3.3 MMC环流抑制控制策略

由于MMC各相上、下桥臂电压之和彼此不一致所引起的桥臂环流含有大量的谐波，不仅会增加换流器的功率损耗，还可能破坏MMC的稳定运行，因此必须采取相应的措施对谐波环流进行抑制。

根据图1可得桥臂环流imk与MMC内部电压、电流特性方程：

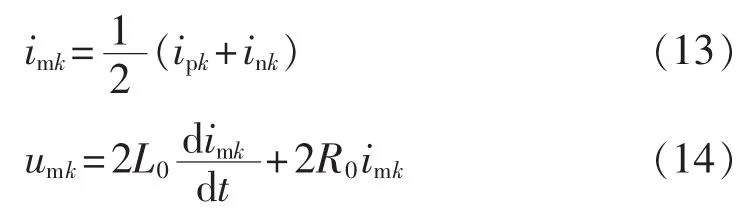
其中，umk为k相的内部不平衡电压降。

文献[17]指出MMC桥臂环流主要含2次、4次、6次等偶次谐波分量，可表示为：

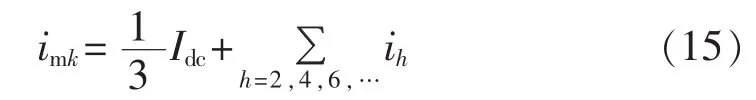
根据式（13）—（15），将桥臂环流中的各次谐波分量视为外部扰动。对其利用扩张状态观测器进行动态补偿，可得基于ADRC原理的MMC环流抑制控制器。对于该一阶系统可不引入跟踪微分器以减少控制器需调节的参数数目，精简后的MMC环流抑制器可表示为：

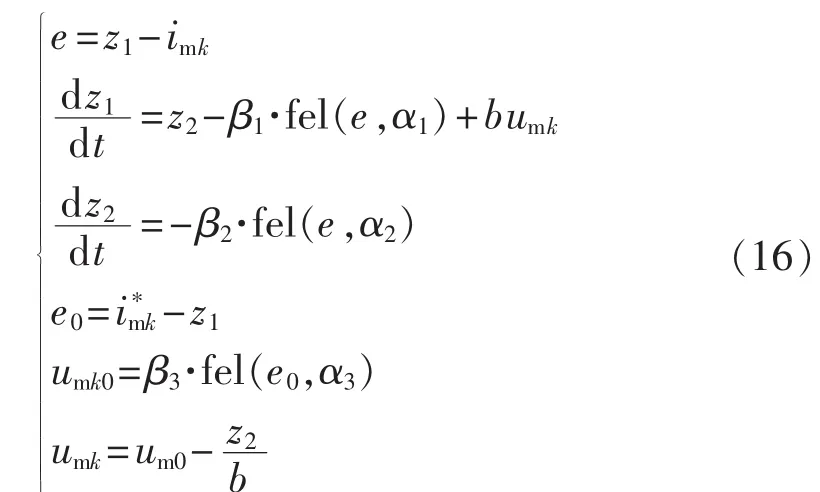
其中，i*mk为桥臂环流参考值，为一直流量，应稳定于：

3.4 MMC 故障不平衡控制策略

在系统发生不平衡故障时，MMC与交流系统之间交换的有功功率与无功功率由于出现负序电压与电流可表示为：

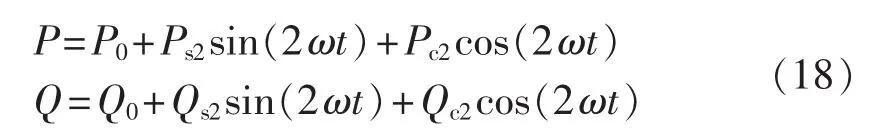
式中各项系数为：

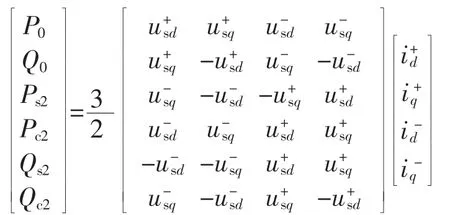
由式（18）可知由于电压、电流负序分量的相互作用，有功功率与无功功率出现了2倍基频的波动，这将造成直流电压出现相应的2倍频波动，并进一步影响对端换流器输出电压与电流波形质量。为保证故障期间电流为三相对称，减少电流不平衡的影响，提高系统的故障穿越能力，必须对负序电流进行抑制。

本文基于ADRC原理设计了一种直接抑制负序电流的控制策略，可表示为：

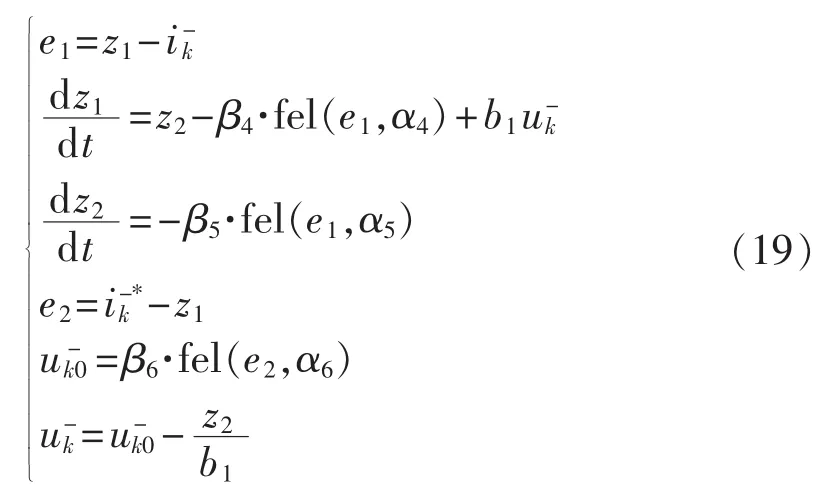
其中，ik-（k=a，b，c）为负序电流实测值；ik-*为负序电流参考值，其值为0；uk-为输出的负序补偿电压。包含环流抑制与负序电流抑制控制器的MMC整体控制原理框图如图7所示。

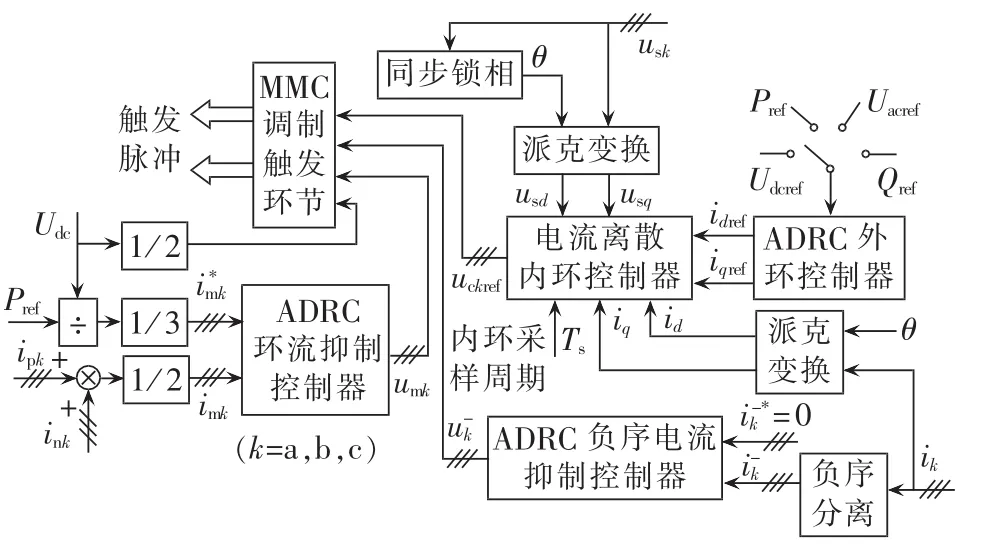
图7 MMC整体控制系统原理框图Fig.7 Schematic diagram of MMC overall control system

4 仿真验证

为验证所设计的基于ADRC原理的MMC控制器的有效性，在PSCAD/EMTDC中搭建如图8所示两端21电平MMC-HVDC。MMC-HVDC参数如下：两端交流系统额定电压220 kV，系统阻抗8.478 Ω；换流变压器T1变比220/230，T2变比220/210，变压器漏抗均为0.1 p.u.；子模块电容C=3000 μF，桥臂L=0.03 H；系统直流电压Udc=±200 kV，直流额定有功功率为400 MW。系统采用最近电平逼近调制，电流内环离散控制器采样周期Ts=200 μs。正常运行时MMC1换流站采用定直流电压与定交流电压控制，MMC2换流站采用定有功功率和定无功功率控制，两端MMC的均压控制策略均采用工程中常用的子模块排序均压法。

图8 MMC-HVDC系统图Fig.8 MMC-HVDC system

4.1 稳态仿真分析

为了验证所设计的控制系统在电网电压平衡条件下的控制性能，MMC2侧有功功率指令Pref2从-1 p.u.到-0.5 p.u.、0、0.5 p.u.、1 p.u.发生一系列阶跃，无功功率指令Qref2从-0.25 p.u.到 -0.1 p.u.、0、0.1p.u.、0.25 p.u.发生一系列阶跃，仿真波形如图9（a）、（b）所示；在此过程中MMC1侧直流电压与交流电压的仿真波形如图9（c）、（d）所示。

从图9（a）、（b）中可以看出，在本文所设计的控制系统作用下，系统的有功功率与无功功率（均为标幺值）能够快速无超调地跟踪外环功率指令，显示了其良好的控制品质。从9（c）、（d）以及桥臂子模块电容电压波形图9（e）、（f）可以看出，所设计的控制系统能够有效降低由有功功率和无功功率发生阶跃瞬间所造成的功率不平衡对系统的影响（直流电压超调量1.35%，交流电压超调量0.91%，子模块电容电压最大波动幅值±3%），显示了所设计的控制器具有良好的抗扰性能。

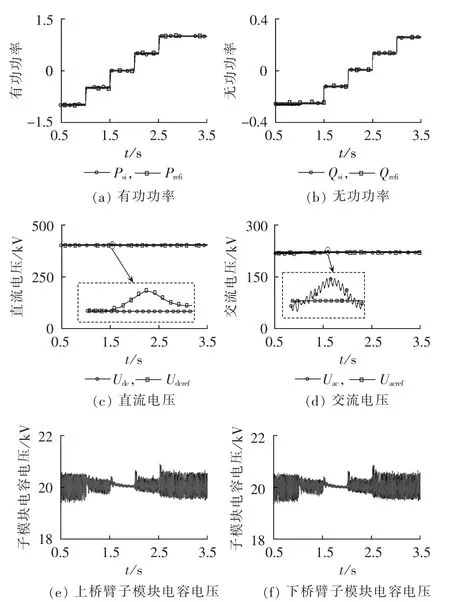
图9 MMC-HVDC稳态仿真波形Fig.9 Simulative steady-state waveforms of MMC-HVDC system

4.2 环流仿真分析

在电网电压平衡工况下，系统有功功率400MW，无功功率0 Mvar，环流抑制控制器在2.0 s时投入，桥臂环流、上桥臂电流以及上桥臂子模块电容电压仿真波形分别如图10（a）、（b）、（c）所示。

从图10可以看出，在2.0 s后桥臂环流稳定在参考值附近，其幅值得到了明显的抑制，桥臂电流波形得到了显著的改善并趋于正弦，子模块电容的波动程度也有明显下降，表明所设计环流抑制器对环流具有很好的抑制作用。

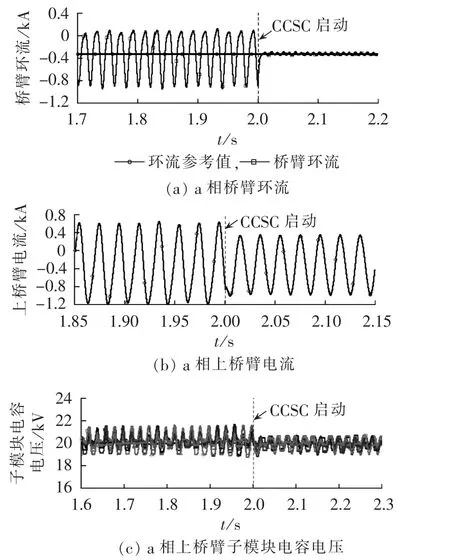
图10 MMC环流抑制仿真波形Fig.10 Simulative waveforms of MMC with circulating current suppression

4.3 暂态仿真分析

在电网电压不平衡条件下，本文以故障率较高的单相接地故障为例，验证所设计的负序电流抑制器的有效性。系统稳态运行时，有功功率为200 MW，无功功率维持在0，2.0 s时，MMC2在靠近交流系统侧发生单相接地故障，电压如图11（a）所示跌落至0.9 p.u.，故障持续时间0.5 s，对比分析系统未采取任何相应控制措施与采取负序电流抑制策略下的仿真波形如图11（b）—（f）所示。

从图11（c）、（d）可以看出，在未采取任何控制措施情形下，三相电流发生畸变，电流的最大值相对稳态运行时增大了1倍；采取抑制负序电流控制策略后，系统电流恢复三相对称，由于故障期间有功功率指令没有发生变化，而负序电流（如图11（b）所示）经抑制后约为 0，从而造成正序电流上升。 图11（e）、（f）表明未加负序电流抑制器前，故障期间由于负序电压与电流的影响，系统有功功率与无功功率出现了较大的波动；投入负序电流抑制器后，系统有功功率及无功功率的波动明显下降，有效地提高了MMC系统的故障穿越能力，表明本文所设计的ADRC原理的负序电流抑制器对负序电流具有良好的抑制作用。

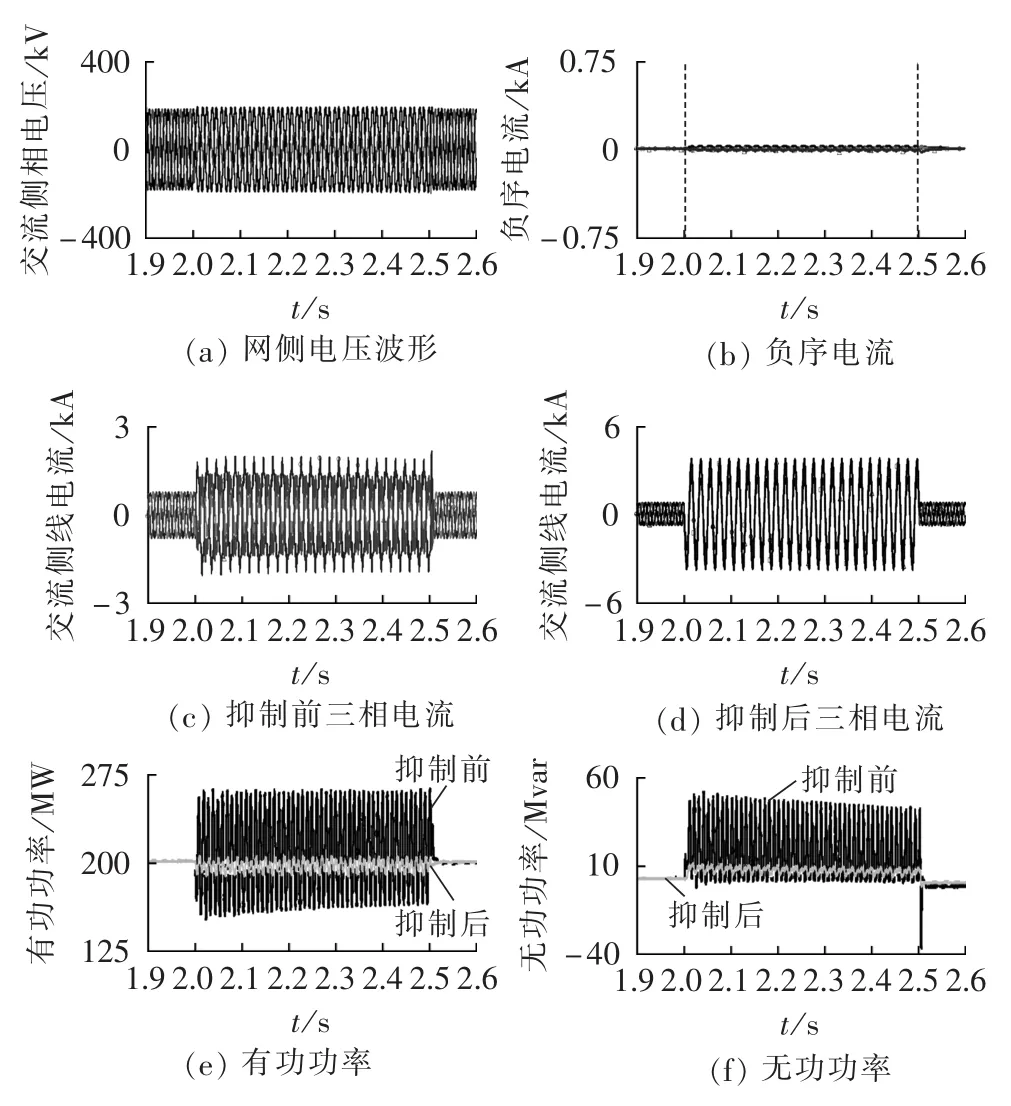
图11 MMC-HVDC暂态仿真波形Fig.11 Simulative transient waveforms of MMC-HVDC system

5 结论

本文基于MMC离散化数学模型建立了MMCHVDC电流离散内环控制器。基于ADRC理论，在已有文献基础上提出一种新型非线性函数，在此基础上设计了MMC-HVDC外环控制器。针对MMCHVDC存在的环流问题，利用ADRC控制器抗扰性强的特点设计了环流抑制器，对桥臂不平衡电容电压进行动态补偿。在电网电压不平衡条件下，采用ADRC控制器设计了负序电流抑制器对三相负序电流进行直接抑制。最后在PSCAD/EMTDC环境下搭建两端21电平MMC-HVDC，验证本文所设计控制器的有效性。仿真结果表明，本文所设计的控制器在稳态运行时能够快速、精确地跟踪系统参考值，且在系统受到外部扰动时具有良好的抗扰性能；所设计的环流抑制器及负序电流抑制器简单、高效，能够有效抑制桥臂环流的谐波分量及提供系统在不平衡条件下的故障穿越能力。