基于配电网静态电压质量机会性约束的可再生能源分布式发电容量规划

周辛南，柯德平，孙元章

（武汉大学 电气工程学院，湖北 武汉 430072）

0 引言

分布式发电技术的快速发展，为可再生能源的开发利用提供了条件。然而，小型分布式电源的无序接入也对配电网运行和调度模式产生了一定的冲击[1-2]。分布式电源经中低压配电网实现并网运行，使配电网由传统的单电源辐射架构变为多供电节点网络，必然引起馈线中有功、无功功率传输的大小及方向发生改变，进而影响配电网的静态电压分布[3-4]。对于薄弱配电网，由于自身线路条件限制，其带负荷能力相对较弱，分布式电源并网运行会造成线路电压升高甚至电压越限，严重影响了配电网的电压质量，分布式发电的并网容量也受到了极大的限制。

文献[5-7]建立了分布式电源选址定容的多目标规划模型，但其前提是分布式电源出力恒定，而可再生能源分布式电源出力受外界环境条件变化影响而呈现随机波动性。文献[8]建立了一种考虑配电网静态电压质量的确定性分布式电源规划模型，保证了系统电压在任何分布式电源出力场景下均满足质量要求，这极大地限制了分布式电源的接入容量，使得规划结果过于保守。然而，如果在某些出现概率很小的极端场景下能适当松弛对系统静态电压质量的要求，分布式电源的可接入容量将可能明显提升。这就要求在含随机性因素的规划环境下放弃使用确定性的静态电压质量评估方法。例如，文献[9]通过对分布式电源的随机性出力进行采样，并结合概率潮流的方法获取各个节点电压的概率密度曲线，实现了对配网静态电压质量的概率评估。进一步，文献[10]则将静态电压不越限的概率作为约束（机会性约束）条件之一来规划分布式电源。除此之外，该文还较全面地考虑了经济效益、环保效益等约束条件，以及负荷和分布式电源出力在时空范围内概率分布的差异性和互补性。但该文通过线性化系统潮流方程并应用半不变量法来计算节点电压的概率分布曲线。因此，对于高度非线性的电力系统而言，其计算精度还有进一步提升的空间。此外，文献[11]在规划分布式电源容量时重点考虑了风机出力相关性对节点电压概率分布的影响。该文所采用的时移技术能直观便捷地形成具有指定相关性系数的2个风速序列，却难以处理多个风速序列相互间相关性的问题。关于形成具有指定相关性系数矩阵的多风速序列问题，文献[12]采用了一种基于Cholesky分解的线性变换方法。该方法原理清晰、计算简单，但是有可能生成负值风速数据[13]。 以该方法为基础，文献[13]通过生成中间序列，并用它们指导原始风速序列重排序来获取满足相关性要求的序列，从而避免了出现负值风速数据的可能。但该重排序方法并非直接以给定的相关性系数矩阵为目标，因而排序的精度还有待提高。特别地，文献[14]计及了规划地区的气候特点，建立了考虑分布式电源出力时序特性的多场景规划模型，但其场景不能保证全面描述分布式电源的出力特性，从而导致优化结果可能偏于乐观。此外，相似的场景近似处理方法也在文献[15]中得到应用，且此文更加偏重于从提高配网静态电压稳定裕度期望的角度来规划分布式电源。

本文首先从配电网自身参数角度分析了分布式电源接入配电网后引起电压升高的机理；建立了一套系统性的考虑配电网静态电压质量机会性约束的分布式电源接入容量规划模型。该模型的特点是在计算静态电压概率分布时使用拉丁超立方采样LHS（Latin Hypercube Sampling）生成多个分布式电源的出力采样序列，并基于差分进化算法重排序LHS序列，从而得到具有指定相关性系数矩阵的场景序列，在充分考虑计算效率的同时明显提高了处理随机性和相关性的精度，保证了规划结果的可靠性。

1 分布式电源接入对配网静态电压的影响

可再生能源分布式电源通过逆变器实现并网运行[16]。根据不同的无功控制目标，该类分布式电源在潮流计算过程中可以建模为PQ、PV、PI、PQ-V等节点类型。随着输出有功功率的变化，这些节点类型的分布式电源影响配网静态电压的过程也各不相同。然而，尽管逆变器能实现灵活的无功控制，但是可再生能源分布式电源的输出无功一般被控制为零。这主要是因为零无功输出的逆变器能充分利用其容量输出有功功率，对于私有化的分布式电源而言，其经济效益能最大化，并降低逆变器损耗；此外，在统一的分布式电源调度管理系统建立之前，调度部门也希望各个分布式电源不要盲目无序地输出无功功率，从而尽量减少对系统正常无功电压控制的干扰；IEEE-1547标准建议：分布式电源应以单位功率因数并网运行[17]。基于以上考虑，本文将以具有广泛代表性的PQ节点类型分布式电源为研究对象[10]，分析其输出有功功率变化对配网静态电压的影响，所采用的简单配网系统如图1所示。图中，无穷大母线0的电压幅值已知且保持不变；分布式电源经逆变器并网在负荷母线1上；R和X分别为线路的电阻和电抗；U1为母线1的电压幅值；PL0和QL0分别为负荷的有功功率和无功功率；PDG为分布式电源发出的有功功率，由于其运行在单位功率因数下，故输出无功功率为0。用PL和QL分别表示母线1的等值有功和无功功率负荷，则 PL=PL0-PDG、QL=QL0。

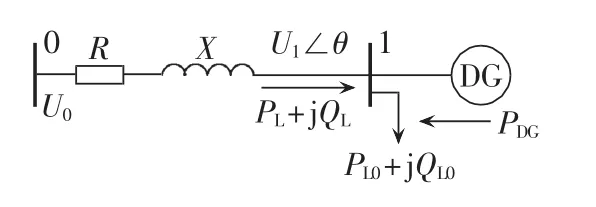
图1 简单配网系统Fig.1 Simple distribution network

从图1根据电压降落的公式可得：

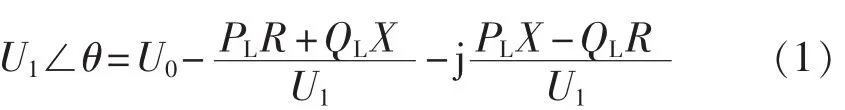
整理得：

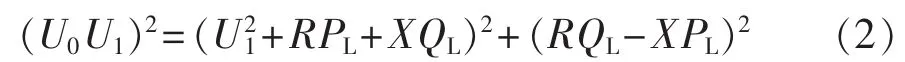
首先，当分布式电源输出功率从0开始逐渐增加（PL从正值开始逐渐减小），部分负荷有功功率将会被补偿，线路电压损耗降低，负荷节点电压升高。当负荷有功完全由分布式电源提供，即PL=0，再继续增加分布式电源输出功率，研究此时节点电压U1的变化规律，可对式（2）两侧求关于PL的导数得：

当PL=0时，网络可传输的无功功率极限为：

由于配网中馈线电阻与电抗数值较大且相差不大，故根据式（3）、（4）知，这说明随着分布式电源出力的增加即PL的减小，节点电压不断抬升。

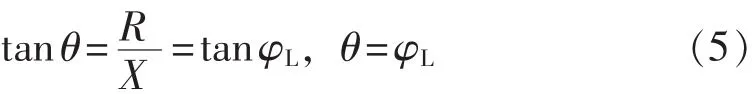
其中，φL为线路阻抗余角。可求得极大电压幅值为：

此时分布式电源注入功率为：

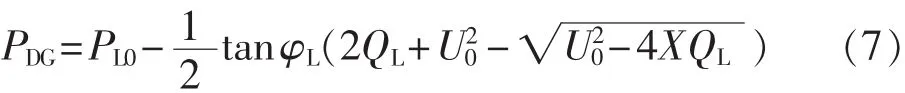
图2 DG接入对配电网静态电压的影响Fig.2 Impact of DG integration on distribution network static voltage

由式（6）和（7）可知，极大值的取得以及其对应的分布式电源注入功率取决于配电网自身参数与所带负荷。以图1系统为例，图2给出了该系统在不同馈线参数状态下静态电压U随分布式电源注入有功的变化趋势（图中横轴、纵轴均为标幺值），其中R/X越小表示配网线路参数越好。可以看出，分布式电源接入配电网后，随着注入功率的增加，线路电压变化趋势有2种情况：逐渐升高；先升高后降低。不同于输电网，配电网中馈线往往线径较小、R/X值较大，分布式电源接入配网出现第2种情况的概率增加，也更可能出现电压超过规定范围的情况[18]。尤其是薄弱的配电网中，线路参数不佳，在分布式电源注入功率较小时，便能使节点电压达到极值，且幅值较大，极易发生高电压越限问题。因此，有必要在规划阶段详细考虑分布式电源对配网静态电压的影响，从而恰当地约束其接入容量。

2 可再生能源分布式电源的容量规划模型

2.1 可再生能源分布式电源出力的随机性及其处理方法

可再生能源分布式电源对外界环境（如风速、光照）的变化十分敏感，其输出功率因此呈现较强的随机性。配网系统静态电压也将由于此类分布式电源的接入而呈现随机性。与传统的确定性约束条件不同，本文将以配网静态电压质量的机会约束为条件来规划分布式电源的接入容量。因此，在有随机性功率输出的分布式电源接入时，量化计算配网静态电压的概率分布将是求解此类电源规划问题的基础。概率潮流法是计算静态电压概率分布的一般性手段。其中，解析性的概率潮流法（如cumulant法、高斯分解法等）虽能快速计算节点电压幅值的累积分布函数CDF（Cumulative Distribution Function），但存在系统潮流方程线性化的假设条件，且仅在节点随机性注入功率呈现类正态分布的情况下有较好的计算结果。众所周知，潮流方程是强非线性方程，且风力发电、光伏发电等分布式电源出力的概率分布与正态分布有较大差异。故此时用解析概率潮流法求解节点电压幅值的累积分布函数可能导致计算结果精度较低。鉴于此，本文将采用基于场景的概率潮流法来计算节点电压幅值的累积分布函数，主要是因为其计算精度不受潮流方程的非线性及分布式电源出力的概率分布影响。特别地，本文将利用LHS法来生成计算所需场景[13]，通过对各分布式电源的输出功率进行抽样，得到一个包含N个采样点的采样序列来表征各自的出力概率分布。接下来需对这些采样序列进行重排序，从而正确反映各分布式电源间出力的相关性。

2.2 分布式电源间出力相关性及其处理方法

由于配网覆盖范围较小，当多个可再生能源分布式电源同时接入配网时，其地理位置相互临近导致其出力具有较强的相关性[11]。图3给出了配网中出力高度（正）相关的2个分布式电源（2台风机）的有功出力曲线；可以看出，其出力变化趋势具有高度的一致性。此外，不同类型的分布式电源如风机和光伏发电系统间出力往往具有较强的负相关性。一般而言，风机夜间出力较大而在午间则相对较弱，而光伏夜间发电为零、在午间达到出力极大值，即二者出力具有一定的互补性。可以简单定性地推论：出力高度正相关的多分布式电源系统所产生的功率波动要明显强于出力高度负相关的系统所产生的功率波动，二者对配网静态电压的影响也将有较大的区别。因此，要对2.1节中生成的各个分布式电源序列进行处理，使其相关性系数符合实际情况。

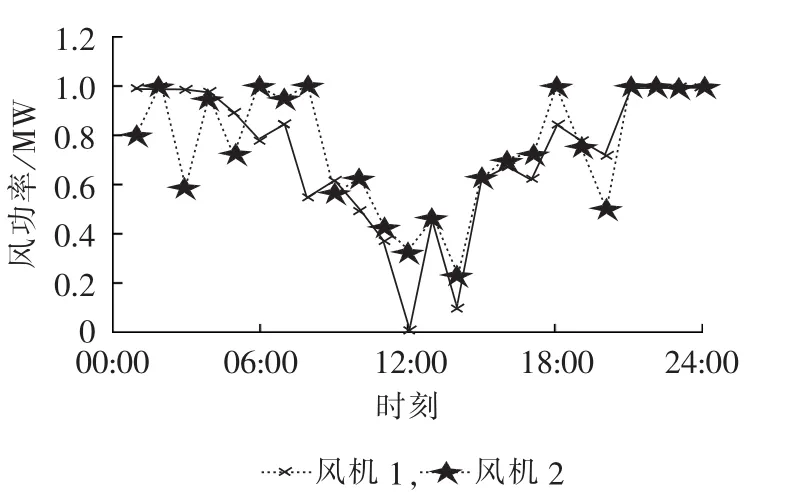
图3 相邻风机处的有功功率Fig.3 Active power of adjacent wind turbines

如引言所述：时移技术难以处理多分布式电源间的相关性问题；而基于Cholesky分解和线性变换的方法在解决相关性问题时可能出现负的风速数据，在此方法的基础上改进而衍生的排序法则可能误差较大。因此，本文提出一种基于差分进化算法的相关性处理方法。假设有M个可再生能源分布式电源接入配网，则根据LHS法可得到M个采样序列。差分进化算法的种群中的每个个体都包含3个分量：第一个分量为序列编号，代表这M个序列中的一个；而后2个分量为位置编号，代表这个序列中的2个位置。对于任一个体，首先选择第一个分量代表的序列，并根据后2个分量将该序列这2个位置上的数据对调，然后在其他M-1个序列保持不变的情况下计算相关性系数矩阵K，最终以矩阵的F-范数‖K-K0‖F（K0为目标相关性系数矩阵，F-范数为矩阵元素平方和的均方根）作为该个体的评价度函数。因此，经过一般差分进化算法的变异、交叉和选择过程，便可将原始的LHS序列不断重排并最终得到具有指定相关性系数矩阵K0的序列。特别地，K0阵可通过历史数据近似预估的方式获得。例如，在2个地区分别规划风力发电项目时，这2个地区的风速历史数据通常可得到，取相同时间段内两地的风速数据，及拟采用的风机的风速-功率曲线，可分别计算得到两地的风机输出功率时间序列，记作X和Y，则K阵中反映这两地风机出力相关性的元素可计算如下：

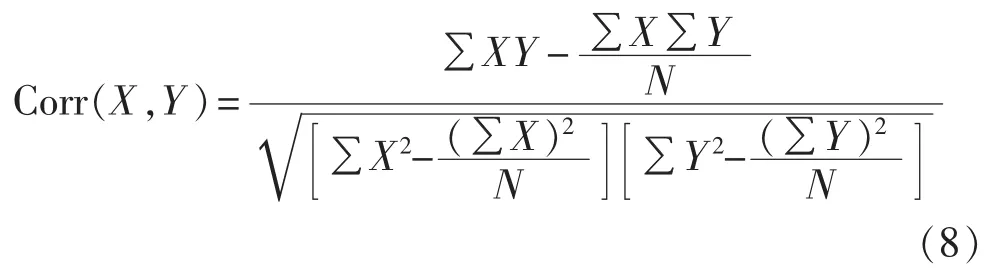
理论而言，在分布式电源规划模型计算过程中，电源容量的改变将要求重新利用LHS法生成新的采样序列，而对新的采样序列则需使用进化算法进行重排序，这样就保证了排序后的序列间的相关性系数矩阵保持为K。然而，根据文献[13]可知：对2个单调递增（或者递减）的序列进行重排序后得到新序列的相关性与排序的方式密切相关，而受原始序列的具体取值的影响则非常小。因此，在规划模型的求解过程中，本文将采用简化的计算方式，即在模型求解初始化阶段对各个序列的重排方式进行一次搜索，使得序列间相关性系数矩阵为K，并记录此排序方式，后续求解过程中针对LHS法生成的新采样序列，则直接使用此排序方式进行重排序。很显然，如此排序得到的新序列间的相关性系数矩阵将与K阵存在一定误差。但大量实验数据表明该误差变化范围较小，且考虑到K阵本身仅是对实际相关性的一种近似估算，因此该简化计算方式具有可行性。更重要的是，这种简化可节省大量的规划模型求解时间。

至此可知，当给定M个分布式电源的容量，则可利用LHS法生成M个N维的采样序列，并对这M个序列进行重排序，排序后的序列可以组成一个N×M阶矩阵，该矩阵的每一行即代表一个场景。对于每一个场景，可以利用常规潮流计算出各个节点的电压。当所有场景下节点电压都计算得到，便可利用统计法获取节点电压幅值的概率分布。

2.3 分布式电源规划模型的建立与求解

本文将以配网系统接入的分布式电源容量加权之和最大为目标建立规划模型，相关的目标函数为：

其中，xi=1表示节点i接入分布式电源，xi=0表示节点i没有分布式电源接入；n为网络节点总数；Si为第i个节点接入的分布式电源的容量；μi为其权重。

约束条件如下。

a.潮流方程等式约束，如式（10）所示。

b.分布式电源容量上限约束，如式（11）所示。

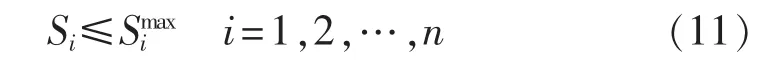
其中，Si为第i个节点接入的分布式电源的容量；Smaxi为第i个节点接入的分布式电源的容量上限。

c.分布式电源出力相关性系数约束，见式（12）。

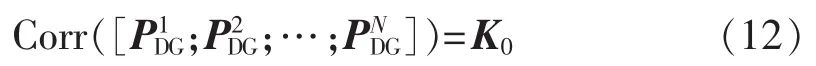
d.配电网静态电压质量机会约束。配网静态电压受所接入的可再生能源分布式电源的影响而呈现随机性。在某些出现概率较小的极端场景下，系统的静态电压可能越限。如果此时以确定性的电压质量要求为约束条件，即要求所有场景下系统的电压质量都要满足要求，则分布式电源的可接入容量将会极大受限。因此，本文将采用如下机会约束的方式来保证系统在随机性环境下的电压质量：

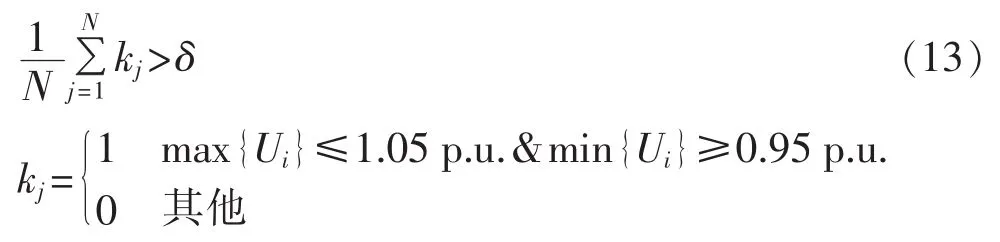
其中，Ui为节点i的电压值；在场景j中，当配电网所有节点电压均运行在安全范围0.95～1.05 p.u.时，kj=1，否则 kj=0。为所有场景下满足电压质量要求的概率，当其大于给定值δ时，认为满足配电网电压质量机会约束。显然，机会约束是允许系统在某些出现概率为1-δ的场景下出现电压越限现象的。当δ取值非常接近1，这些场景出现的概率将非常小。此外，即使出现了电压越限现象，也可通过切除分布式电源和部分负荷的方式来改善系统电压。电压质量的机会约束将有可能较大地松弛分布式电源的可接入容量。

上述模型为混合整数非线性规划模型，由于其涉及随机采样和概率潮流计算，很难运用确定性规划理论对其求解；人工智能算法[19-20]可获取全局最优解，本文采取差分进化算法[21]进行求解。步骤如下。

a.初始化。随机产生NP个初始种群，即随机产生分布式电源的初始接入容量。

b.评价初始种群。对分布式电源随机出力进行采样，按照相关系数矩阵要求进行重排序并记录此排序方式，通过概率潮流计算和规划模型中的其他约束条件，对初始种群进行评价，获取最优个体和最优目标函数值，若此时个体不满足约束条件，选取最接近要求的个体为最优个体。

c.交叉变异。处理边界条件，产生下一代种群。

d.选择。将产生的新种群即分布式电源容量传回给采样程序，按照记录的重排序方式调整采样序列，重新进行概率潮流计算，根据约束条件的满足情况和目标函数值的大小，选出最优个体和最优解。

e.终止条件判断。若满足终止条件或进化代数，则进化终止；否则，进化代数niter=niter+1，转步骤c。

优化的结果与权重的选取密切相关。为了使结果更贴近实际，本文期望各个点接入的分布式电源容量不宜相差太大。因为目前尚缺少高效且通用的权重选取方法，本文将采用简单的试错法：设定所有权重初始值为1，μi=1，优化计算得到规划结果；如果结果不满足期望，适当减小容量过大的分布式电源所对应的权重并相应增加容量较小的分布式电源所对应的权重，再次执行优化计算；此过程持续进行下去，直到得到合理的计算结果。

3 算例仿真及结果分析

本文采用如图4所示的标准IEEE33节点配网系统作为仿真算例，其基准电压为12.66 kV，基准容量为 10 MV·A。

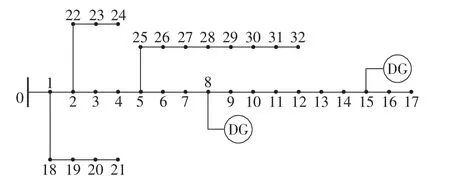
图4 IEEE 33节点配网系统Fig.4 IEEE 33-bus distribution network

假设在节点8和15上有分布式电源接入。为了验证本文所采用的随机性和相关性处理方法的有效性，假设节点8和15上接入2台容量均为1 MW的风机，并利用蒙特卡洛随机采样生成2个序列来模拟这2台风机的实际出力。特别地，随机采样的样本空间需要足够大（此处取为20000）以使得这2个序列能分别拟合各自风机出力的概率密度函数曲线，同时能满足指定的相关性系数（此处取为0.3）要求。与之构成比较的是利用本文所采用的LHS和基于差分进化算法重排序所得到的2个序列（样本空间为500）。分别基于这2种方法所获取的风机出力序列执行概率潮流计算，统计各个节点电压的累积分布函数曲线并对比于图5。此外，当假设节点8接入容量为1 MW的光伏电源且其与节点15的1 MW风机的出力相关性为-0.4时，同样地执行上述对比过程并将结果示于图6。

从图5和图6可看出，无论是在正相关还是负相关的情况下，基于LHS和差分进化算法重排序所得到的节点电压的概率分布都与其实际概率分布（基于蒙特卡洛模拟生成）非常接近，从而验证了本文方法处理随机性和相关性的准确性。在本算例中，由于样本空间巨大，基于蒙特卡洛随机采样的概率潮流计算共耗时约为175.86 s；而基于本文采样排序方法的概率潮流计算仅耗时约为3.97 s。二者计算时间的比较均在一台配置为Intel Core i5-4590 CPU，8 G内存（计算性能相对较突出）的台式电脑上完成。因此，本文所采用的求取节点电压概率分布的方法的效率在当前的计算能力和条件下仍然是可以接受的，这也保证了后续基于此概率潮流计算的可接入容量优化搜索在计算效率上的可行性。

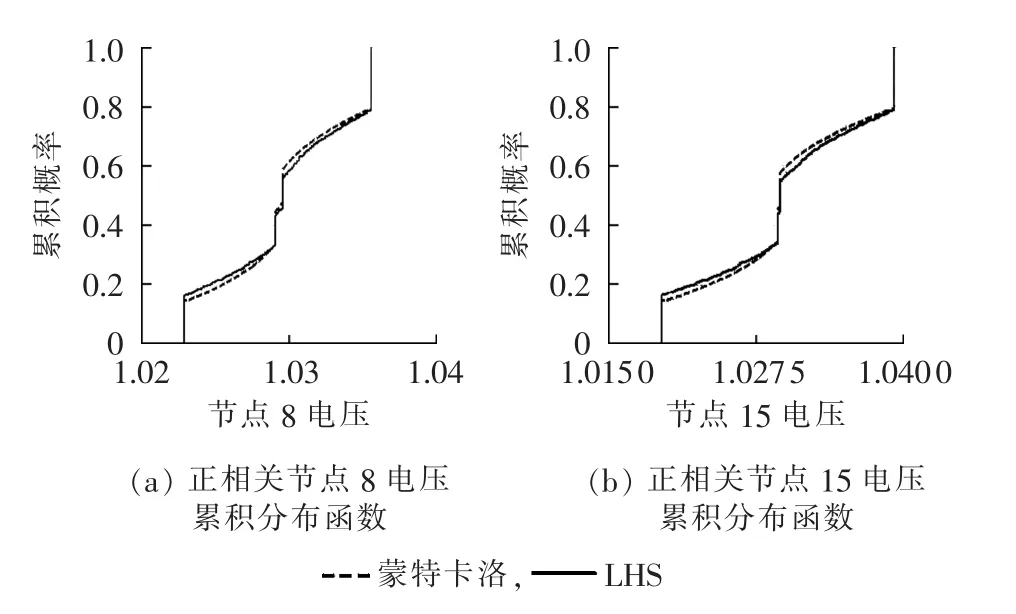
图5 正相关情况下基于蒙特卡洛和LHS方法的概率潮流得到的节点电压幅值概率分布Fig.5 Probability distribution of node voltage amplitude obtained by probability power flow based on Monte Carlo and LHS method in condition of positive correlation

图6 负相关情况下基于蒙特卡洛和LHS方法的概率潮流得到的节点电压幅值概率分布Fig.6 Probability distribution of node voltage amplitude obtained by probability power flow based on Monte Carlo and LHS method in condition of negative correlation

当节点8和15上均接入基于风机的分布式电源时，利用本文方法规划它们的最优接入容量。差分进化算法参数设置如下：种群数量NP=20；变异算子F=0.9；交叉算子CR=0.9；迭代次数最大值nitermax=100。静态电压质量合格概率约束δ=0.95。分别设定两风机出力相关性系数为0（不相关）、0.3（中度相关）和0.8（高度相关）3种情况，表1给出了规化结果的对比，其中SDG8、SDG15分别为在节点8、15接入的分布式电源容量。表中数据均为标幺值，后同。

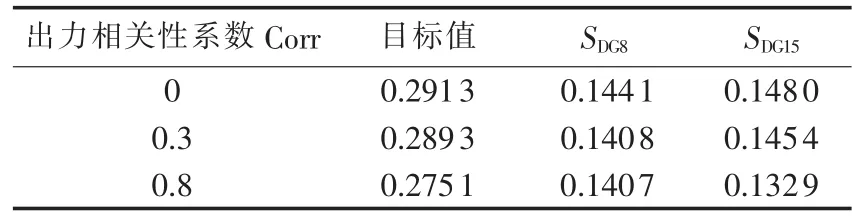
表1 风电规划结果Table 1 Planning results of wind power

风机出力的相关性直接影响了配电网消纳其接入容量的能力。从表1中可以看出，随着2台风机出力相关性的增大，节点8和15上的风机可接入容量逐渐减小。这是因为正相关性越高，分布式电源出力变化趋势一致性愈强（即同步性越强），其对系统影响的叠加效果也越强，节点电压因此而出现的波动性也越大。在出力高度相关的条件下，保障系统静态电压合格的概率就需要压低分布式电源的接入容量。此外，如果在规划过程中未考虑分布式电源的相关性，则节点电压实际越限概率可能会超过设定值；规划结果偏于乐观，给配电网运行造成安全隐患。

将节点15的风机替换成光伏发电，节点8仍接入风机，运用本文提出的方法规划二者的接入容量。分别考虑二者出力不相关和负相关（相关性系数为-0.6）2种情况，规划结果对比于表2。

表2 风光规划结果Table 2 Planning results of wind power and photovoltaic power

从表2中可以看出，较之出力不相关的情况，风机和光伏出力的负相关性导致其可接入容量均有所提升。因为分布式电源出力负相关性使得节点电压的波动性减小，减小了节点电压越限的可能，增强了系统消纳分布式电源的能力。此种情况下，若不考虑分布式电源间的互补性，便会限制分布式电源的接入容量，使规划结果过于保守。

对比表1和表2，不难发现配电网能消纳更大容量的互补性分布式电源。对于同类型分布式电源，因地理位置接近，出力趋于同步，配网静态电压受其影响明显，因而其允许接入容量也相对较小。而互补性分布式电源，其出力峰值错开，同时接入时具有削峰填谷的作用，出力同时达到最大（小）的概率极小，基于此，配电网容许的互补性分布式电源容量会相对较大。仿真结果也说明了在分布式电源规划过程中准确考虑其出力随机性和相关性的重要性。

4 结论

本文研究了分布式电源接入配电网造成高电压越限的机理；提出了一套系统性地考虑分布式电源出力随机性和相关性，以及配电网静态电压质量机会约束的分布式电源接入容量规划方法，并利用差分进化算法进行了求解，得到以下结论。

a.配电网静态电压一般随分布式电源出力的增加呈先增大后减小的趋势。由于薄弱的配电网馈线参数较差、R/X较大，极有可能在分布式电源出力容许范围内，造成配电网高电压越限。故有必要以静态电压质量为约束来详细规划分布式电源的接入容量。

b.配电网中分布式电源地理位置接近，外界条件相似，同类型分布式电源出力具有高度正相关性，导致节点电压波动较大，造成电压越限的概率也随之增大，使得配电网消纳分布式电源容量的能力减小。若不考虑分布式电源出力的相关性，将会使规划结果偏于乐观，给配电网运行造成安全隐患；不同类型分布式电源，如风电与光伏，具有一定的互补性，使得节点电压波动减小，若在规划过程中忽略其相关性，便限制了分布式电源的接入容量。算例仿真结果也验证了本文致力于在规划过程中提高处理分布式电源出力随机性和相关性精度的必要性。