油浸式变压器三维电磁-流体-温度场耦合分析方法

廖才波，阮江军，刘 超，文 武，王珊珊，梁嗣元

（1.武汉大学 电气工程学院，湖北 武汉 430072；2.国网电力科学研究院武汉南瑞有限责任公司，湖北 武汉 430074）

0 引言

作为电网中的主要电气设备，电力变压器对电能的经济传输、灵活分配、安全使用等具有重要意义。电力变压器的运行状态直接关系到电网的稳定性，而在实际运行中，绝缘问题及热问题是影响变压器运行状态的关键因素，其中变压器过热将加速绕组绝缘劣化，影响变压器使用寿命。变压器各类问题的出现使得变压器多物理场研究逐渐受到研究者的重视，至今已能较好地揭示变压器电磁、力学和结构方面的物理特性，然而对于变压器发热冷却问题，研究则相对薄弱。目前，针对变压器热点温升计算的方法主要包括经验公式法[1-2]、热路模型法[3-5]和数值模拟法[6-13]，其中经验公式法将变压器热点温度定义为环境温度、顶层油温和热点温度与顶层油温之间的温差三者之和，且针对不同类型的变压器给出了不同的计算参数，在实际工程中具有一定的适用性；热路模型法主要通过热电类比建立变压器的热路模型求解变压器热点温度，但求解结果与热路模型中参数设定密切相关；2种计算方法在一定程度上忽略了变压器结构及散热介质对热点温度的影响。为了更加系统地了解变压器内部温度分布，研究学者提出了基于流体力学和传热学的数值模拟法，通过建立变压器模型进行温度场求解分析，但由于变压器内部结构较为复杂，在计算过程中对变压器模型进行了较大的简化，且变压器损耗求解主要采用经验公式进行计算，存在一定的计算误差。多物理场弱耦合分析方法的提出一定程度上提高了变压器温度场求解的准确度，但目前的分析大多基于变压器二维轴对称模型，且忽略了变压器温度对绕组损耗的影响，会影响温度场求解结果的精度[14]。

因此，本文提出了基于有限元法和有限体积法的变压器三维电磁-流体-温度场耦合计算方法用于模拟变压器内部热特性，首先通过建立变压器有限元模型进行磁场分析并求解变压器铁芯及绕组损耗，将变压器损耗作为流体-温度场加载条件进行热分析，再根据热分析结果对变压器绕组损耗进行修正，通过多次迭代计算求解变压器温度分布。本文以35 kV油浸自冷式变压器为计算对象进行三维变压器电磁-流体-温度场耦合分析，通过热点温度计算结果与经验公式法进行对比验证该方法的正确性。

1 理论基础

1.1 磁场控制方程

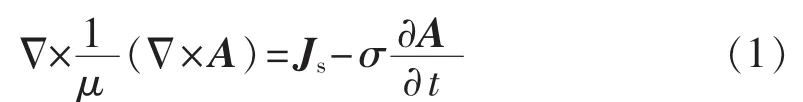
其中，μ为磁导率，单位为H/m；σ为电导率，单位为S/m；A为矢量磁位；Js为变压器绕组的电流密度，单位为 A/m2。

变压器运行过程中，变压器热源主要来自于铁芯及绕组损耗，其中变压器铁芯损耗大小与铁芯内部的磁通密度分布密切相关，因此须先对变压器内磁场分布进行求解计算。参照麦克斯韦方程组，基于矢量磁位的变压器磁场的控制方程如式（1）所示[15]。

1.2 流体-温度场控制方程

对于油浸式变压器，变压器铁芯及绕组产生的热量主要经变压器油循环对流传送至变压器油箱，再通过变压器油箱外壁散热达到冷却的目的。对于不可压缩的理想流体，变压器油在油箱内的流动及分布特性主要受质量守恒定律、动量守恒定律和能量守恒定律控制，如式（2）所示[16]。

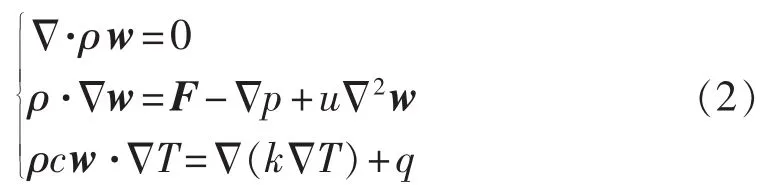
其中，ρ为变压器油密度，单位为kg/m3；w为变压器油流速，单位为m/s；F为外部体积力，单位为N；p为压力，单位为N；u为变压器油动力粘度，单位为N·s/m；c为变压器油比热容，单位为 J/（kg·K）；T 为温度，单位为 K；k 为热导率，单位为 W/（m·K）；q 为变压器损耗，单位为W/m3，可由前文磁场分析计算变压器铁芯及绕组的单位损耗得到，而外部热源如太阳照射对变压器温度的影响主要通过环境温度的设定体现。

变压器油箱散热方式主要包括与外界空气的自然对流换热及辐射散热，其中对流散热占主导地位，计算中忽略辐射散热的影响。变压器油箱对流散热的控制方程如式（3）所示。

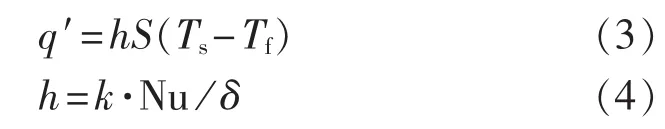
其中，h为变压器油箱的对流换热系数，单位为W/（m2·K），可由式（4）求解得到；S 为变压器油箱的散热表面积；Ts为油箱表面温度，Tf为空气温度，单位为K；δ为特征长度，单位为m；Nu为努谢尔数，自然对流下的垂直和水平平面努谢尔数求解分别参照式（5）和式（6）。

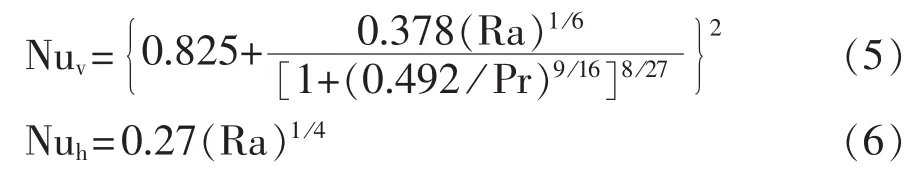
其中，Ra为雷利数，Pr为普朗特数，两者均为传热学中的无量纲参量。

1.3 电磁-流体-温度场耦合分析

采用电磁-流体-温度场顺序耦合仿真方法求解变压器内部温度分布时，先采用有限元法进行变压器时谐磁场分析求解铁芯及绕组损耗，其中变压器绕组损耗与绕组温度相关。在求解得到变压器损耗之后，采用有限体积法进行流体-温度场分析求解变压器内部温度分布，根据绕组温度对绕组损耗加以修正，进行迭代计算重新求解变压器流体-温度场，并计算相邻两步温度计算误差，在计算误差满足收敛要求后（温差小于0.1 K）停止计算，计算流程图如图1所示。

变压器三维电磁-流体-温度场耦合分析中，主要根据绕组温度修正绕组损耗，考虑到绕组损耗中绕组直流损耗占主要部分，而绕组电阻与温度呈线性关系，可得绕组损耗随温度变化的关系见式（7）。

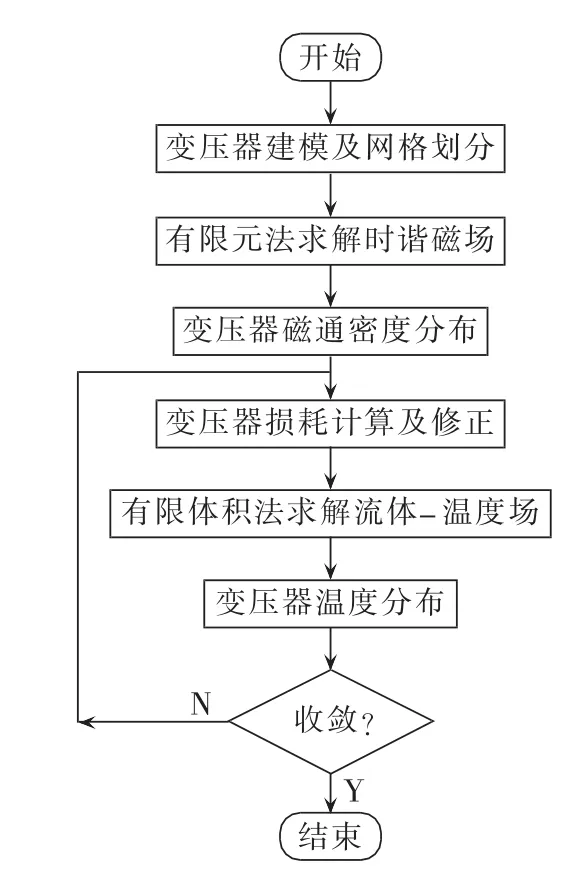
图1 变压器电磁-流体-温度场耦合仿真流程图Fig.1 Flowchart of comprehensive simulation of electromagnetic-fluid-thermal fields

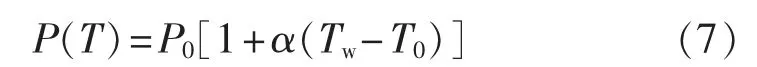
其中，P0为初始温度T0时计算得到的绕组损耗；Tw为流体-温度场求解得到的绕组温度；α为导体温度系数，对于铜导线，α取0.00393。

2 计算算例

2.1 变压器模型

本文以某6300 kV·A、35 kV油浸式变压器为计算对象进行三维电磁-流体-温度场耦合分析，计算变压器内部温度分布。变压器的主要参数为：高压侧额定电压为35 kV，绕组内半径为268.5 mm，外半径为316.5 mm，绕组高731 mm；低压绕组额定电压为10.5 kV，绕组内半径为195.5 mm，外半径为247 mm，绕组高724 mm；变压器铁芯采用30Q130型硅钢片，铁芯重4322kg；变压器油箱尺寸为2.233 m×0.969 m×1.853 m，采用自然油循环冷却方式。根据主要参数建立变压器三维计算模型，铁芯及绕组如图2所示。

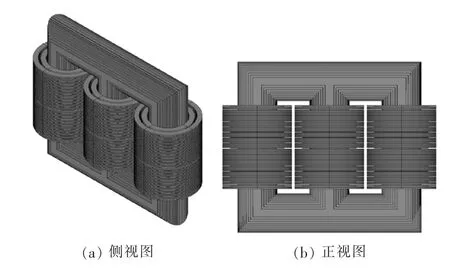
图2 变压器铁芯及绕组模型Fig.2 Model of transformer core and windings

2.2 变压器三维磁场计算

变压器磁场计算中，主要考虑变压器高、低压绕组、铁轭绝缘和绝缘筒对变压器磁场分布的影响，各部分的材料参数如表1所示。

表1 变压器磁场分析所需参数Table 1 Parameters for transformer magnetic field analysis

采用有限元法进行变压器三维时谐磁场计算，低压绕组加载变压器空载电流，高压绕组开路，可得空载情况下变压器铁芯的磁通密度分布如图3所示。

图3 变压器铁芯磁通密度分布（空载）Fig.3 Magnetic flux density distribution inside transformer core（without load）

变压器运行过程中，铁芯损耗主要由铁芯中的磁通产生，该部分损耗主要包括磁滞损耗、涡流损耗及附加损耗。因此，根据求得的磁场结果，采用式（8）计算单位质量的铁芯损耗[17-18]。

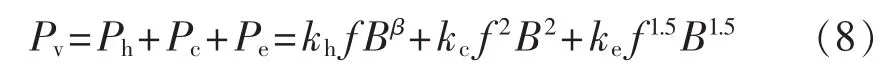
其中，Ph为磁滞损耗；Pc为涡流损耗；Pe为附加损耗；f为频率；B 为磁通密度最大值；kh、kc、ke和 β 为未知系数，具体数值可由硅钢片损耗表拟合得到，对于30Q130型硅钢片，各参数如表2所示。

表2 30Q130型硅钢片损耗系数Table 2 Loss coefficients of silicon steel sheet 30Q130

计算得变压器单位质量的铁芯损耗为0.6995 W/kg，乘以变压器铁芯质量便可得变压器空载损耗大小为3.0232×103W。在变压器三维时谐磁场计算中加载变压器高、低压绕组额定电流，则可计算得到变压器额定电流下的绕组损耗，计算过程与空载情况相同，求得变压器绕组损耗数值如表3所示。

表3 变压器损耗计算值Table 3 Calculated transformer losses

2.3 变压器三维流体-温度场计算

在变压器三维流体-温度场计算中，流体场迭代计算的收敛性对模型网格质量要求较高，且在模型网格数量较多时，计算过程复杂，因此在变压器三维磁场模型基础上对变压器进行简化。首先，考虑到变压器采用自然油循环冷却方式，绕组间横向油道内部油流速度极小，对绕组温度影响较小，因此在三维流体-温度场计算模型中忽略绕组横向油道，将变压器绕组简化为圆筒形，但保证绕组损耗总量不变。同时，忽略变压器箱体外壳安装的散热片，参照式（3），变压器油箱总散热量与油箱散热面积及油箱外壳对流换热系数成正比，为了保证变压器外壳散热总量不变，按照忽略散热片前后散热面积之比同比例增大变压器外壳的对流换热系数。变压器三维流体-温度场计算模型内部结构如图4所示。

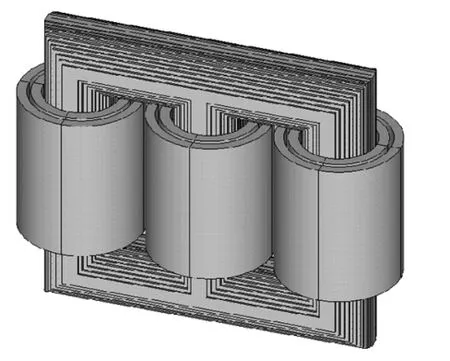
图4 变压器三维流体-温度场计算模型内部Fig.4 Internal part of 3-D fluid-thermal field model of transformer for calculation

变压器三维流体-温度场计算中，主要将其划分为高压绕组、低压绕组、变压器铁芯、变压器油箱以及各固体结构与箱体之间的油流5个区域，各部分的材料参数如表4所示。

计算中，变压器油箱底部温度设为环境温度296.15 K，变压器油箱表面与空气的对流换热系数为23.2 W/（m2·K），变压器油流采用层流模型。采用有限体积法对变压器流体-温度场进行迭代求解，最终求得变压器铁芯以及绕组温度分布计算结果如图5所示。

计算结果表明，变压器热点温度为348.660 K，出现在中相低压绕组上端，三相绕组中以中相绕组温度最高，温度差值小于0.5℃。变压器铁芯温度最大值为326.540 K，出现在铁芯芯柱靠近低压绕组上端，铁芯整体温度分布处于323.750 K与326.540 K之间。高压绕组温度最大值为339.250 K，出现在高压绕组上端。观察高、低压绕组温度分布可以发现，虽然高压绕组的损耗大于低压绕组，但由于低压绕组散热条件较差，低压绕组整体温度分布高于高压绕组。

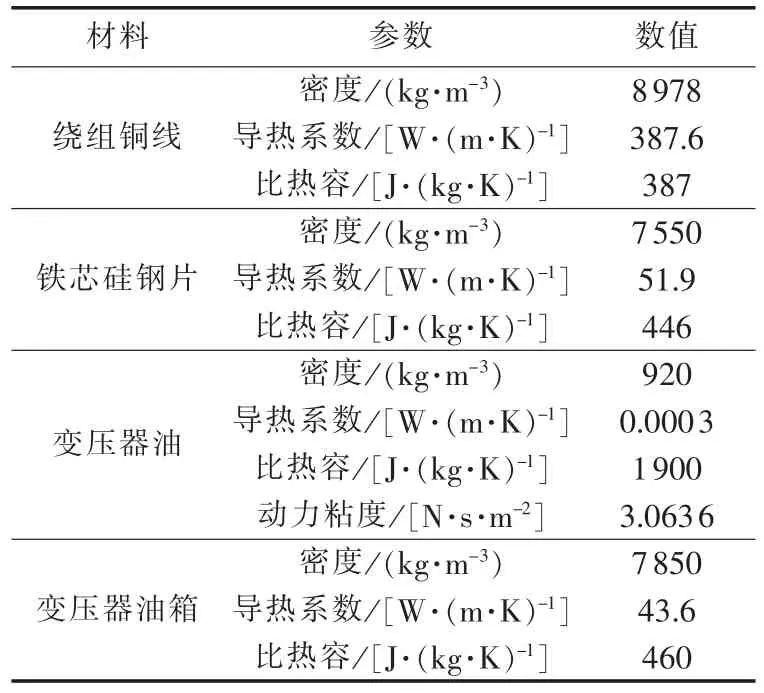
表4 变压器流体-温度场分析所需材料参数Table 4 Parameters of transformer materials for fluid-thermal field analysis

图5 变压器温度分布计算结果Fig.5 Calculated temperature distributions inside transformer

变压器油流速度是影响变压器铁芯及绕组温度的重大因素之一，计算得变压器内部油流速度分布矢量图如图6所示。

图6 变压器油流速度分布图Fig.6 Oil flow velocity distribution inside transformer

计算结果表明，变压器油流速度最大为4.527×10-3m/s，且变压器上铁轭附近油流速度较大，主要原因在于上铁轭附近绕组顶端温度较高，油流流动剧烈。为了更加清楚地观察变压器内部油流分布，分别以变压器铁芯对称面为观测面，取得各切面的油流速度分布如图7所示。

观察xoy和yoz切面结果可以发现，油流速度较大处主要集中在上铁轭附近，且油流速度沿y方向分量较大。观察xoz切面结果发现，变压器绕组间以及绕组和铁芯之间轴向油道内油流速度较小，低压绕组的散热条件较差，可考虑通过增大高、低压绕组的间距改善低压绕组散热条件；高压绕组外侧油流速度明显大于内侧，高压绕组散热条件优于低压绕组，其温度分布亦低于低压绕组；且xoz切面的整体油流速度分布小，各相绕组间油流速度相对较大。另外，变压器绕组周围及沿油箱内壁油流速度较大，主要原因在于变压器绕组温度较高，变压器油流受热沿绕组周围向上铁轭运动，在上铁轭周围与铁轭进行热交换，随后沿着变压器油箱内壁向下运动。

3 绕组热点温度计算验证

对于采用饼式绕组结构的油浸式变压器，绕组温升 θr可由式（9）计算得到①沈阳变压器有限责任公司.油浸式变压器设计手册.2002.。

其中，τr为绕组与油平均温升的温差，对于自冷式变压器内、外绕组，分别采用式（10）、（11）计算；θy为油平均温升，可由式（12）计算得到。

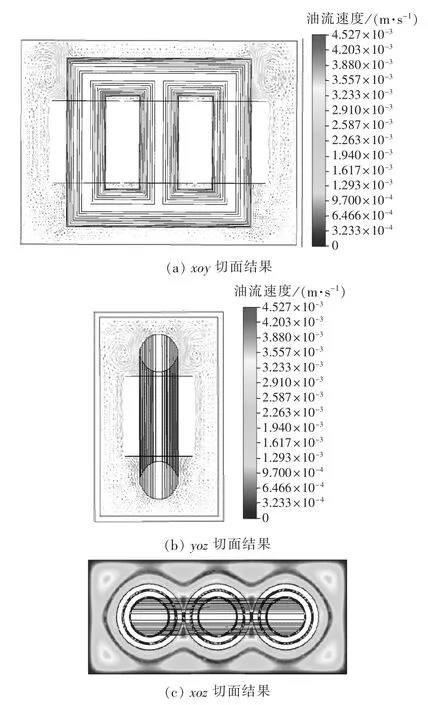
图7 油流速度切面结果Fig.7 Sectional planes of oil flow velocity

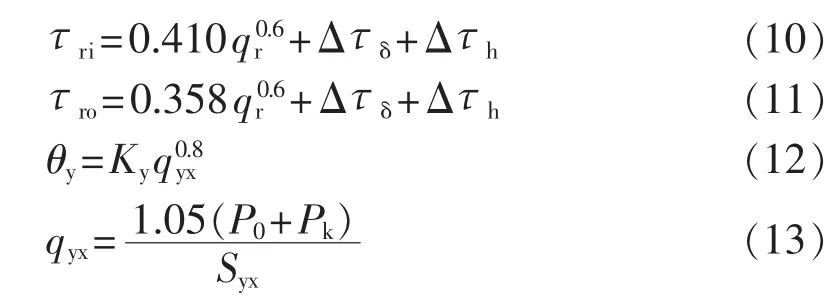
其中，qr为绕组的热负载；Δτδ为绕组的绝缘校正温差；Δτh为绕组的线段油道校正温差；Ky为油平均温升计算系数，油浸自冷式取为0.262；qyx为油箱的热负载；P0和Pk分别为空载损耗和负载损耗；Syx为油箱的有效散热面积。

根据变压器相关参数可以计算得变压器高、低压绕组的热点温升，与仿真计算结果对比，结果如表5所示。

表5 多物理场耦合仿真结果与经验公式计算的温度对比Table 5 Comparison of temperatures between multifield simulation and empirical formula calculation

计算结果表明，采用本文所述多物理场耦合仿真计算方法得到的绕组温升高于经验公式计算结果，但相对误差小于4%，符合工程应用的要求。因此，本文采用的基于有限元法和有限体积法的变压器三维电磁-流体-温度场耦合仿真分析是有效且正确可信的。

4 结论

本文提出了一种基于有限元法和有限体积法的变压器三维电磁-流体-温度场耦合分析方法。首先采用有限元法进行变压器时谐磁场分析，计算变压器铁芯及绕组损耗，并将其作为后续流体-温度场分析的加载热源，随后采用有限体积法求解变压器三维流体-温度场获取变压器铁芯及绕组温度分布，根据绕组温度分布对变压器绕组损耗进行修正，重新迭代求解流体-温度场，直至相邻计算步之间温差小于0.1 K。采用本文所述方法对35 kV油浸式变压器进行三维电磁-流体-温度场仿真，计算了变压器铁芯、绕组温度分布及变压器内部油流分布，将绕组热点温度计算结果与经验公式计算结果相对比，验证了本文方法的正确性和有效性。