含经VSC-HVDC并网海上风电场的交直流系统概率最优潮流
2015-09-21李逸驰孙国强黄文进卫志农孙永辉
李逸驰,孙国强,杨 义,黄文进,卫志农,孙永辉
(1.河海大学 可再生能源发电技术教育部工程研究中心,江苏 南京 210098;2.盐城供电公司,江苏 盐城 224005)
0 引言
随着经济的发展,化石能源与环境之间的矛盾日益突出,开发和利用新能源已经成为世界共识。风能作为一种清洁、可再生的绿色能源在世界范围内得到越来越广泛的应用[1-2]。同陆上风电相比,海上风电具有风速高、噪声小等优点。自1990年丹麦安装第一台海上风电示范机组以来,海上风电技术得到快速发展,2011年亚洲首个柔性直流示范工程——上海南汇风电场直流输电工程投运,标志着我国在柔性直流输电领域已处于世界领先水平。远距离传输的海上风电通常采用基于电压源换流器的高压直流输电VSC-HVDC(Voltage Source Converter based High Voltage Direct Current) 进 行并网[3-4],VSC-HVDC具有实现有功、无功独立控制和向无源网络供电等优势。因此,发展基于VSC-HVDC并网的海上风电是未来风电发展的新趋势。
最优潮流OPF(Optimal Power Flow)是电力系统网络规划和运行分析的重要工具。由于风电场出力的随机性和间歇性,传统确定性最优潮流已无法适用,因此需要考虑计及不确定因素的概率最优潮流 POPF(Probabilistic Optimal Power Flow)。 POPF是一种随机分析方法,它可以根据随机变量的已知概率信息,求取状态变量和控制变量的概率分布情况。海上风速是决定海上风电场出力的主要因素,由于风速的不确定性受地理、气候等多方面因素的影响,因而海上风速的分布情况同陆上风速之间存在差异,目前鲜有文献讨论海上风速的分布情况[5]。针对风电场的出力模型,现有文献多假设风电场出力和风速满足一定函数关系[6],即当风速确定以后风电场出力也随之确定,实际风电场出力并不仅由当前时刻风速决定,还受前一时段的风速和风向等条件的影响[7],因而用一条曲线来代替风电场的功率特性会带来一定误差。
POPF问题的处理方法主要分为模拟法[8]和近似法[9-11]。 基于简单随机采样的蒙特卡罗模拟[8]SRS-MCS(Simple Random Sampling Monte Carlo Simulation)法是求解POPF最为传统的方法,具有精度高的优点,但缺点是效率低。近似法的求解方法主要分为点估计法[9-10]和一次二阶矩法[11],该方法具有效率高的优点,但结果精度有限。因而,针对POPF的求解方法,如何在计算效率和精度之间寻求平衡是一个值得研究的问题。
首先,本文采用非参数核密度估计方法拟合得到海上风速分布。采用最小二乘法拟合得到风电场的功率特性曲线,并考虑拟合误差的概率分布。建立VSC-HVDC的稳态模型,并推导交直流系统的稳态潮流方程。然后,采用拉丁超立方采样LHS(Latin Hypercube Sampling)方法生成标准正态分布样本,利用等概率变换理论和Nataf变换技术得到具有相关性的输入变量样本。接着,基于原对偶内点法进行确定性OPF计算,得到输出变量的数字特征和概率分布。最后,通过算例分析,验证了本文所提方法的正确性和实用性,具有良好的工程应用前景。
1 风电场和VSC-HVDC模型
1.1 风电场的概率模型
风速大小是决定风电场出力的主要因素,大量研究表明,陆上某一地区的风速近似服从Weibull分布。然而,目前为止,国内外学者针对海上风速分布的研究还比较少,尚无统一的分布形式[5]。因而本文采用非参数核密度估计[12]直接根据海上风速样本拟合得到风速分布,该方法避免了假设分布与实际分布不符以及参数估计带来的误差。假设X1、X2、…、XN是某一海上位置的N个风速样本,则该地区海上风速概率密度函数的核估计为:
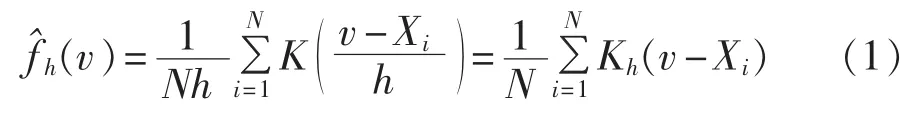
其中,h表示带宽;v表示场内平均风速;N表示样本容量;K(·)表示核函数,常见的核函数有三角核函数、高斯核函数等。
地理位置相近的风电场之间的风速存在较强的相关性。本文采用相关系数矩阵描述各风电场内风速的相关性,K座风电场风速的相关性用如下形式表示:

风电场由安装在同一位置的几十甚至上百台风电机组组成。由于风电场内风机类型和功率特性不尽相同,并且存在尾流效应和场内电气损耗的影响,因而风电场的功率特性曲线不能简单地由单台风电机组的功率特性曲线叠加得到。本文使用风速和风电场出力的历史数据作为样本,采用最小二乘法拟合得到风电场整体的功率特性曲线[7]。
采用与单台风电机组功率曲线相似的切入风速、额定风速、切出风速的经典模型来表示风电场的输出功率特性,同时考虑功率特性曲线和实际出力之间的误差,用如下形式表示:
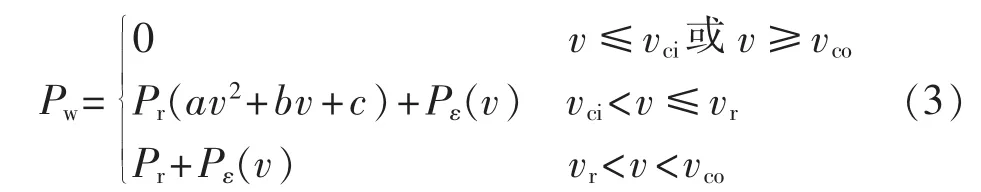
其中,Pw表示风电场的输出功率;Pr表示风电场的额定功率;v表示场内平均风速;a、b、c表示功率特性曲线的系数;vci、vr和vco分别表示切入风速、额定风速和切出风速;Pε(v)表示风电场实际功率误差,是一个与风速v有关的随机变量,其概率密度函数如式(4)所示。
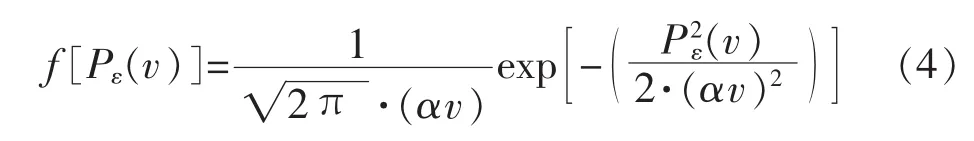
其中,α表示风电场功率误差的标准差与当前风速之间的比例系数。
假设风电机组均为基于双馈感应电机的变速风电机组,采用恒功率因数控制技术[14]。因而在稳态分析时,风电场可以看作PQ节点,若功率因数为cosφ,则风电场的无功出力Qw为:

1.2 VSC-HVDC稳态模型
基于VSC-HVDC并网的海上风电的模型如图1所示。
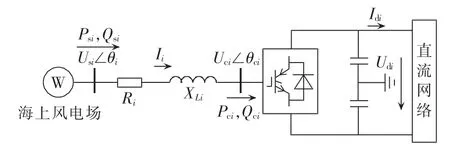
图1 VSC-HVDC模型Fig.1 Model of VSC-HVDC
方程(6)—(13)构成了 VSC-HVDC 的稳态模型。具体推导过程和变量说明参见文献[15]。
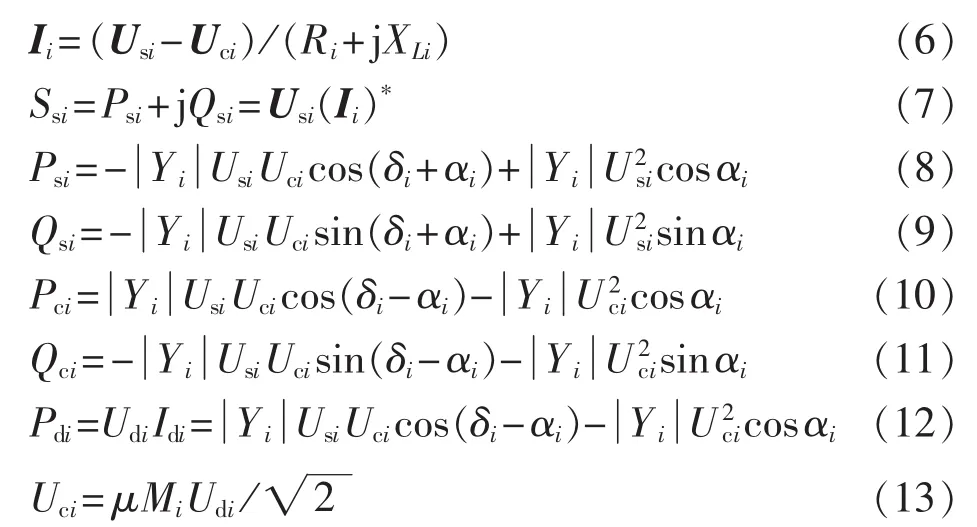
在实际风电场并网应用中,为了保证风电场有功功率的传输,维持风电场母线电压的稳定,风电场侧VSC的控制方式通常采用定交流电压和定有功功率控制[16]。为了实现系统功率的平衡,必须有一端VSC控制其直流电压,因而电网侧VSC采用定直流电压和定交流电压控制[16]。海上风电经VSC-HVDC并网方式主要分为集中型、分组型和直流母线型3种[17],其中集中型是目前海上风电普遍采用的并网方式,因而本文主要讨论集中型并网的海上风电场。
含VSC-HVDC交直流系统的潮流方程包括交流系统功率平衡方程、VSC-HVDC的输入输出功率平衡方程和直流网络的电流平衡方程,如下所示:具体变量说明参见文献[15]。 式(14)—(16)同时构成了含VCS-HVDC交直流系统OPF的等式约束。
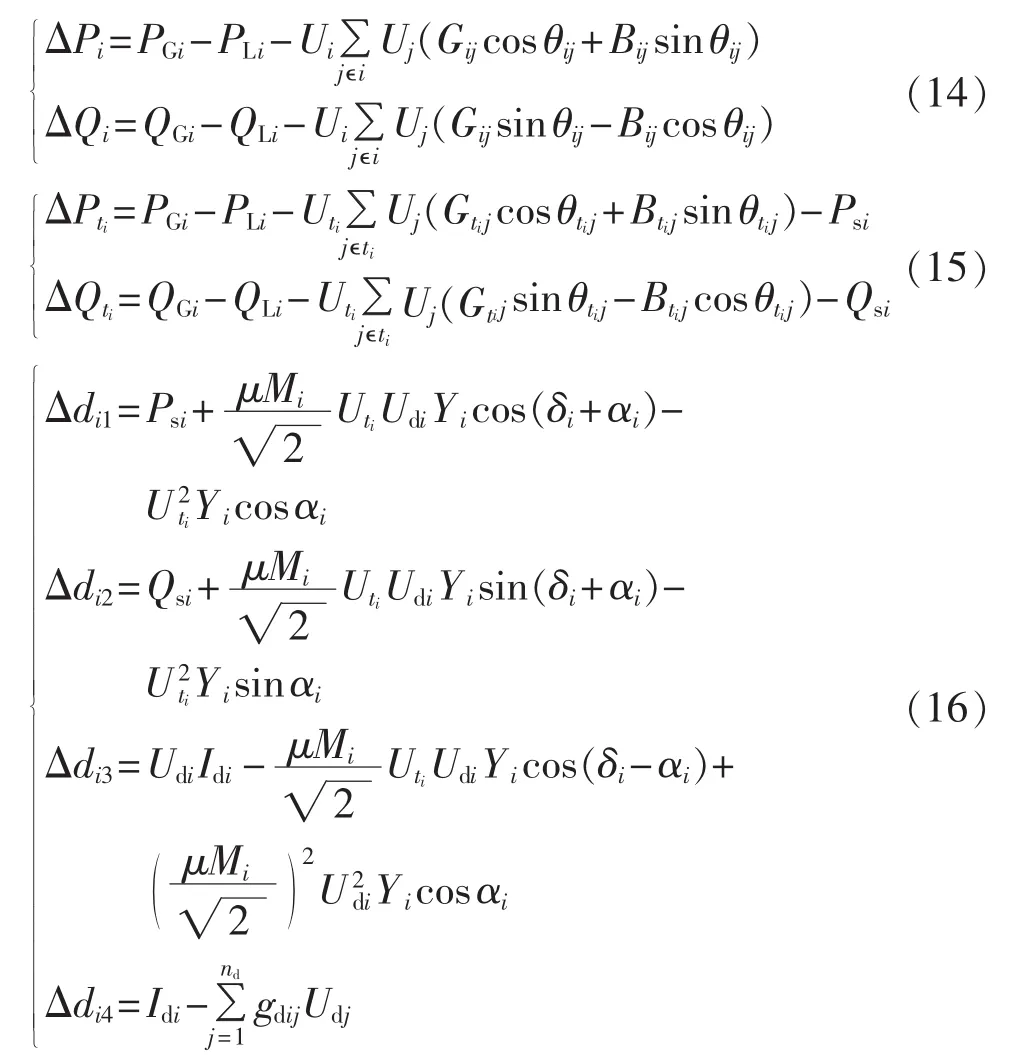
2 基于LHS方法的POPF模型
2.1 相关性处理方法
实际风速存在一定相关性,忽略相关性会对计算结果带来影响。本文采用等概率变换理论和Nataf变换技术得到具有相关性的任意分布的风速样本。
设风速向量为V=[v1v2… vK]T,由1.1节分析可知,第i座风电场风速概率密度函数为fi(vi),概率分布函数为Fi(vi),风速的相关系数矩阵为Cv。根据等概率变换理论,将风速样本转化为标准正态分布样本:

其中,yi表示标准正态分布的随机变量;Φ-1(·)表示标准正态分布的逆概率分布函数。
根据Nataf变换理论,推导得到标准正态分布的随机变量的相关系数矩阵Cv0满足如下关系:
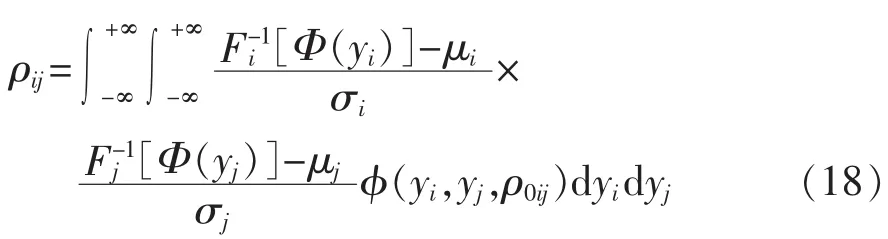
其中,μi表示第i座风电场风速的期望;ρ0ij表示Cv0第 i行、第 j列的分量;φ(yi,yj,ρ0ij)表示相关系数为ρ0ij的二维标准正态分布联合概率密度函数。
通过Hermite多项式展开的方法求解式(18),得到等效相关系数矩阵Cv0,该方法具有较高的精度,同时避免了无穷积分的计算,具体步骤参见文献[18]。
对求解式(18)得到的相关系数矩阵进行Cholesky分解得到下三角矩阵B0:

2.2 LHS方法
LHS是一种分层采样的方法[19-20],主要思想是通过产生更加均匀的样本来提高计算效率。LHS主要流程分为采样和排序2个步骤。
采样的目的是产生已知分布的样本。假设要生成R组样本容量均为N的标准正态分布样本,首先在0~1之间N等分的每个区间内采样一次,然后利用反变换得到标准正态分布的采样值。对于R个随机变量依次采样,得到R×N阶采样矩阵。
排序是对已经得到的样本矩阵进行重新排序的过程。首先对各个随机变量的样本独立地进行随机排序,此时各随机变量样本间的相关系数接近零。然后,利用2.1节提出的相关性处理方法,将R组独立标准正态分布随机变量样本转化为满足一定相关性的任意分布的样本。
2.3 确定性OPF模型
以对发电厂商单侧开放的市场为例,将待解变量用x表示,则OPF模型可以用以下形式表示:

然后,根据Nataf逆变换,将独立标准正态分布随机变量U转化为相关标准正态分布随机变量Y:

最后,根据式(17)的逆变换得到具有相关性的风速样本:
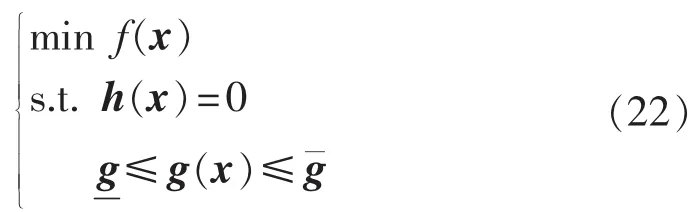
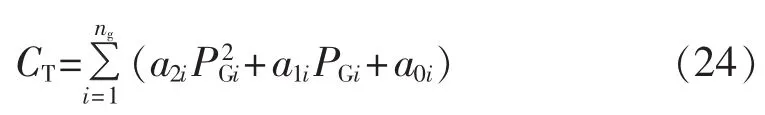
其中,a0i、a1i、a2i表示第 i台常规发电机的成本系数;PGi表示第i台发电机的有功功率;ng表示常规发电机组数量。
海上风电场的发电费用由3个部分组成,分别是海上发电的直接发电费用、海上风电输出功率低估
以发电费用最小作为目标函数,包括常规发电机组和海上风电场的发电费用:

其中,CT表示常规发电机组的发电费用;Cw表示海上风电场的发电费用。
常规发电机组的经济曲线用二次函数来描述:造成浪费的惩罚和输出功率高估带来的备用费用:
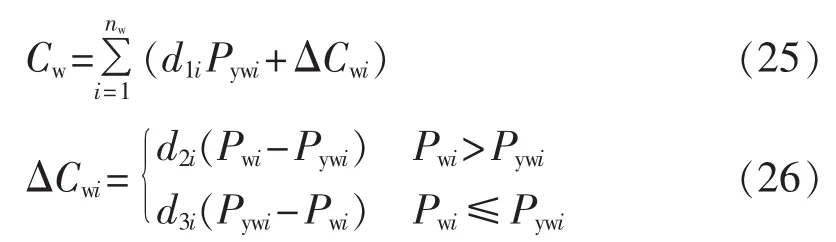
其中,Pwi、Pywi分别表示第i座风电场的实际输出功率和预测功率;d1i、d2i和d3i分别表示第i座风电场的直接成本系数、低估惩罚成本系数和高估备用成本系数;nw表示海上风电场的数量。
通过1.1节的非参数核密度估计利用实际风速和预测风速的数据,拟合得到实际风速v和预测风速 vy的概率密度函数分别为 f(v)和 f(vy),考虑到实际风速和预测风速间具有一定的相关性,利用2.2节的LHS方法得到具有相关性的实际风速和预测风速样本。最后,利用1.1节的风电场功率特性模型即可得到风电场的实际输出功率和预测功率的样本。
式(14)—(16)构成了含 VSC-HVDC 交直流系统OPF的等式约束。不等式约束包括交流系统发电机和风电场出力约束、节点电压和线路功率约束、VSC的调制比和功率约束以及直流节点的电压约束。
原对偶内点法的基本思想是引入松弛变量将不等式约束转化为等式约束,引入障碍函数对松弛变量进行约束,由此构造拉格朗日函数如下:
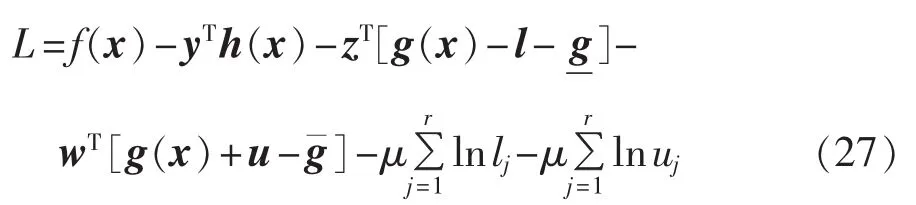
其中,l= [l1,…,lj,…,lr]T、u= [u1,…,uj,…,ur]T表示松弛变量;z和w表示拉格朗日乘子;μ表示障碍函数的罚因子。
该问题的库恩-塔克KKT(Karush-Kuhn-Tucker)条件可以描述成一组非线性方程组,利用牛顿拉夫逊法求解该非线性方程组,具体过程参见文献[15]。
2.4 POPF流程
本文主要考虑风电场出力和负荷的不确定性,不考虑输变电元件故障的不确定,利用2.2节的LHS方法得到含相关性的风电场出力和负荷的样本。对每组样本利用2.3节的OPF模型进行计算,得到输出变量的样本,应用统计学方法计算输出变量的数字特征和概率分布。具体流程图如图2所示。
3 算例分析
3.1 IEEE 14节点系统
以文献[21]提供的IEEE 14节点系统为例,对线路和发电机进行修改,采用基于LHS-MCS的POPF模型(LHS-POPF)进行计算。
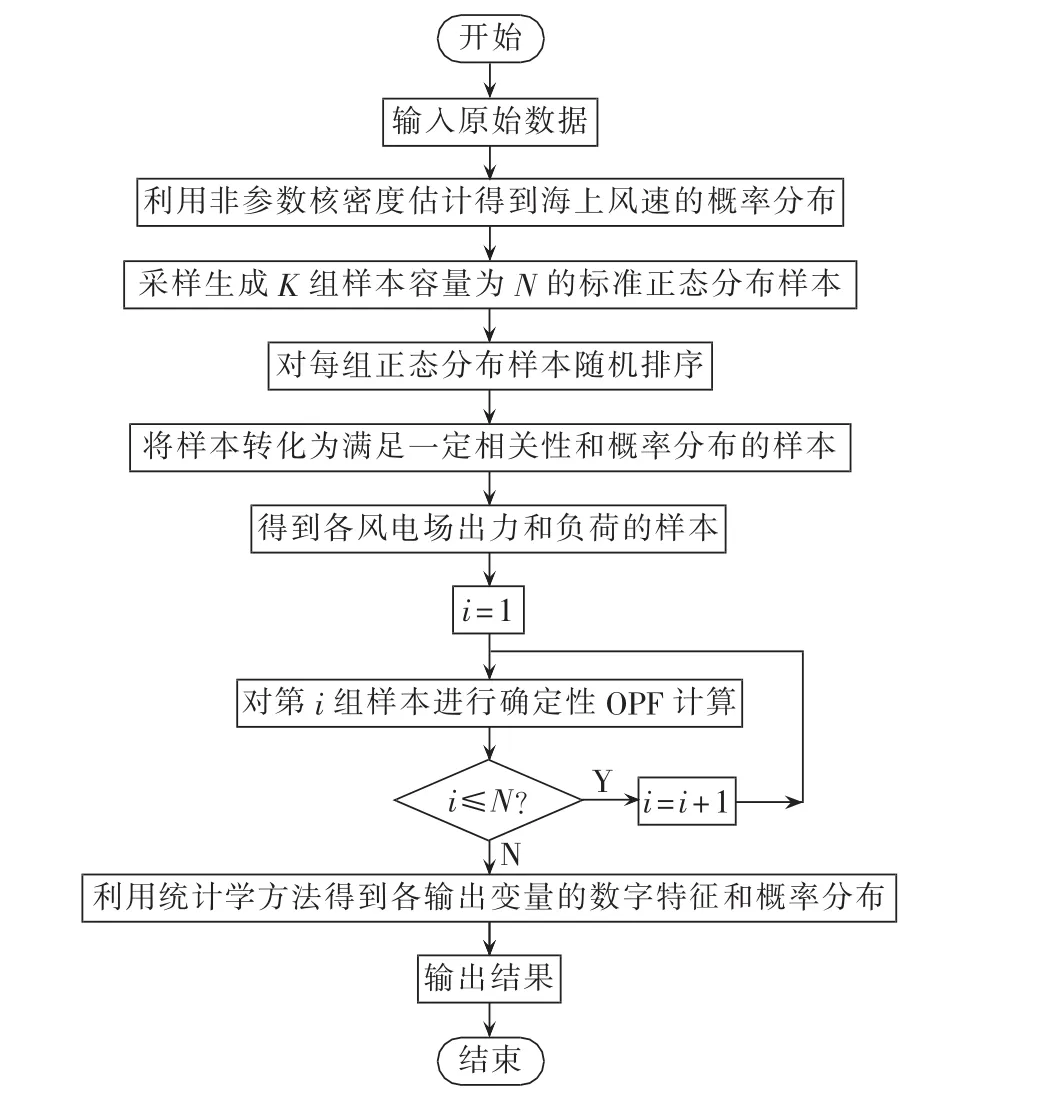
图2 POPF的计算流程图Fig.2 Flowchart of POPF calculation
IEEE 14节点系统共有5台发电机、11个负荷和20条支路。将节点8处的常规发电机组替换为海上风电场,保持额定功率不变。单台风机的切入、额定和切出风速分别为3 m/s、12 m/s和22 m/s,并且以恒功率因数0.96运行。利用非参数核密度估计得到海上风速的概率密度函数,如图3所示。从图3可以看出利用非参数核密度估计根据海上风速的历史数据可以直接得到风速分布,能够客观描述风速的分布特性。假设预测风速和实际风速为同分布的随机变量,预测风速和实际风速的相关系数取为0.8。风电场的直接成本系数、低估惩罚成本系数和高估备用成本系数分别取为 10/(MW·h)、30/(MW·h)和 70/(MW·h)。
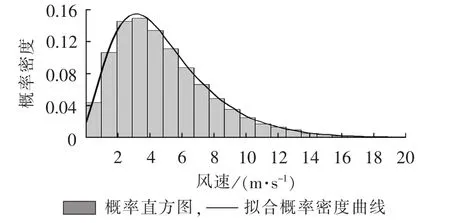
图3 风速概率密度曲线Fig.3 Probability density curve of wind speed
假设负荷服从正态分布,算例中给定负荷数据作为负荷的期望,取负荷期望的5%作为标准差。在节点7、8处安装VSC装置,将支路7-8替换为直流线路后得到交直流系统,直流线路参数见文献[15]。VSC变量范围按照式(28)进行约束:
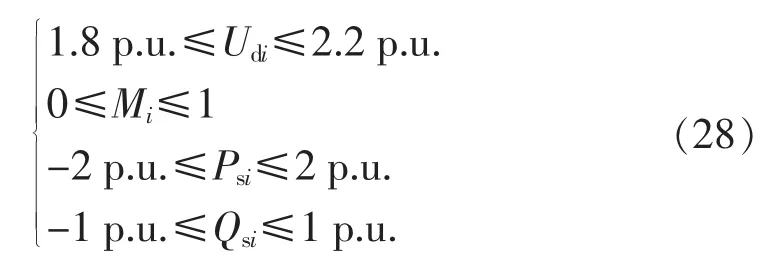
分别对下面2种方案进行计算。
(1)方案1:海上风电场经VSC-HVDC并网。
(2)方案2:海上风电场直接并网。
采用样本容量为500的LHS-MCS方法进行采样,对这些样本分别进行确定性OPF计算,得到最优发电费用、各发电机出力、节点电压、支路潮流和直流系统参数等样本。最后,利用统计学方法得到这些输出变量的数字特征和概率分布。
最优发电费用的概率分布和数字特征如图4和表1所示。从表1可以看出,方案1的最优发电费用期望小于方案2,对于该系统而言,风电场经VSCHVDC并网比直接并网具有更高的经济性。
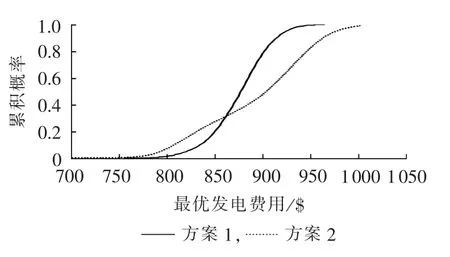
图4 最优发电费用的概率分布曲线Fig.4 Probability distribution curve of optimal generation cost
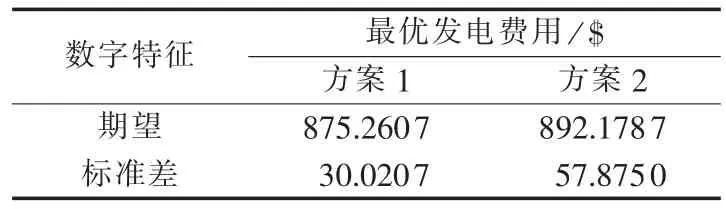
表1 最优发电费用的数字特征Table 1 Numeric characteristics of optimal generation cost
方案1所得部分节点电压的概率密度函数如图5所示,图中节点电压幅值为标幺值。从图5可以看出,本文所提方法能够有效得到各节点电压的概率特性,为运行分析人员提供有效信息。
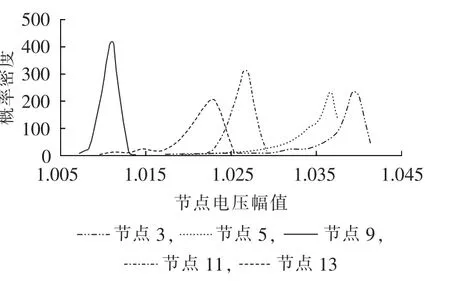
图5 节点电压幅值的概率密度曲线Fig.5 Probability density curve of node voltage magnitude
3.2 IEEE 118节点系统
以文献[21]提供的IEEE 118节点系统为例,对线路和发电机进行修改。IEEE 118节点系统共有54台发电机、99个负荷和179条支路。将节点10和节点73处的常规发电机组替换为海上风电场,保持额定功率不变,单台风机的切入、额定、切出风速和运行方式与算例1相同。2座风电场间的风速存在相关性,取2座风电场风速的相关系数为0.7。负荷服从正态分布,期望和标准差按照算例1方法求得。在节点9、10、71、73处安装VSC装置,将支路9-10和71-73替换为直流线路后得到交直流系统。
针对上述2种方案分别进行计算,所得最优发电费用的数字特征如表2所示,所得各节点电压幅值的数字特征如图6和图7所示(纵轴均为标幺值)。

表2 最优发电费用的数字特征Table 2 Numeric characteristics of optimal generation cost
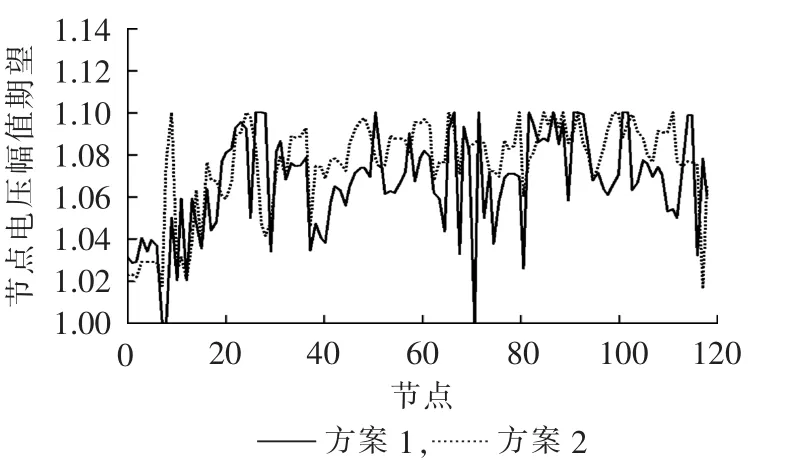
图6 节点电压幅值的期望Fig.6 Expectation of node voltage magnitude
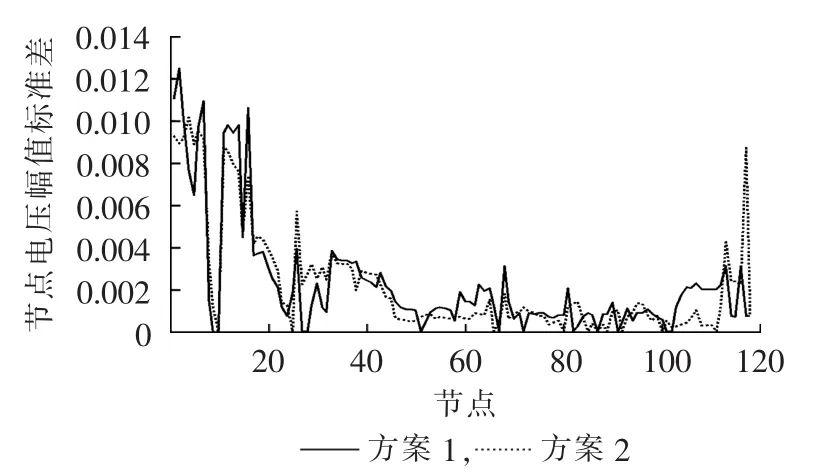
图7 节点电压幅值的标准差Fig.7 Standard deviation of node voltage magnitude
表2所得结果进一步说明了,风电场经VSCHVDC并网具有更高的经济性。由图6和图7可以看出,忽略对VSC-HVDC的建模会使POPF计算结果偏离实际运行情况。
以电压幅值在(0.9,1.1)p.u.区间内作为电压允许的偏移范围,求出2种方案下部分节点的电压越限概率(其余节点的电压越限概率为0)如表3所示。由表3可以看出,风电场经VSC-HVDC并网情况下,由于VSC-HVDC对系统电压的调节能力,能够显著减小部分节点的电压越限概率,提高系统的电压水平,有利于系统的稳定运行。
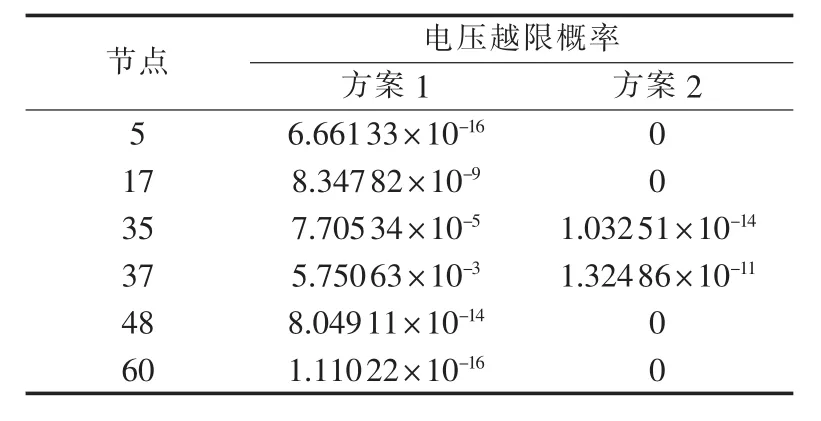
表3 部分节点电压越限概率Table 3 Voltage limit violation probability of partial nodes
通过IEEE 14和IEEE 118节点系统验证了VSC-HVDC对于系统经济性的提高作用。对于IEEE 14节点系统,由于所加风电场的额定功率较小,系统各节点均不存在电压越限情况。对于IEEE 118节点系统,考虑2座风电场同时接入的情况,验证了VSC-HVDC对于系统电压水平具有积极作用。
4 结论
本文分别以IEEE 14和IEEE 118节点系统为例,计算了含经VSC-HVDC并网海上风电场的交直流系统的POPF。算例表明:
a.相比于直接并网,风电场经VSC-HVDC并网具有更高的经济性;
b.VSC-HVDC对系统最优潮流分布有显著的影响,VSC-HVDC能够减小部分节点电压越限概率,提高系统电压水平;
c.本文提出的POPF计算方法能够有效处理海上风速的不确定性和相关性,得到输出变量的数字特征和概率分布,为运行人员提供有效信息,具有良好的工程实用价值。
