非线性矩阵方程X+A*X-qA=Q的Hermite正定解

霍金丹，梁丽，于娇

(东北林业大学)

0 引言

在这里要给出方程

正定解存在的充分和必要条件，其中A是n阶非奇异复矩阵，Q是n阶Hermite正定阵，且q≥1，X为未知矩阵，这样的非线性矩阵方程在梯形网络，随机过滤，动态规划和统计中应用广泛［1-2］，同时通过众多的学者的研究学习也取得了一定的成绩.

该文中遇到的难题都可以根据Banach的不动点定理和Brouwer不动点定理来解决，接着根据方程(1)正定解存在的充分和必要条件求出方程的解，最后又给出了求解方程(1)正定解的另一种方法，即迭代法，与此同时又给出了推导迭代法收敛的一个充分条件.

1 引用定理

引理 1.1［5］令B∈Cn×n，U∈Cn×k，V∈Ck×n且B，B-UV是非奇异的，则

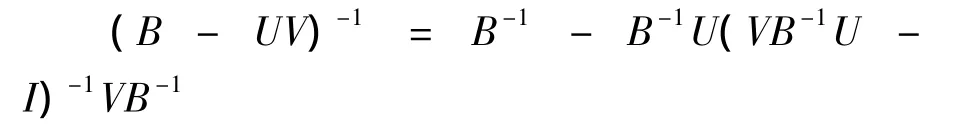
引理1.2［6］令A和B是Hilbert空间H上的正算子，且

M1Ⅰ≥A≥m1Ⅰ≥0，M2Ⅰ≥B≥m2Ⅰ＞0和B≥A＞0，

则

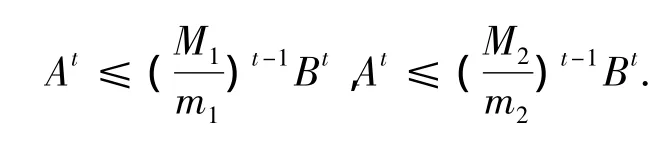
引理1.3［7］令f为在(0，∞)上的单调函数的算子，且令A、B为两个与a有关系下界的正定算子，即A＞aⅠ和B＞aⅠ，其中a为正数，如果存在f＇(a)，则对于每一个酉不变范数‖·‖，有

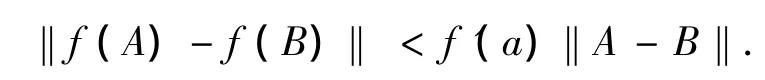
2 主要定理及证明

定理2.1 如果方程(1)有一个正定解X，则

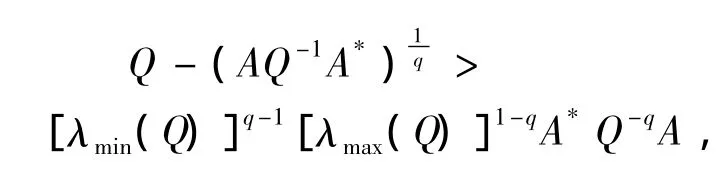
且X∈ (S，T)，这里

证明 由于X是方程(1)的一个正定解.则有X＜Q，A*X-qA＜Q，根据不等式性质，后一个不等式可变为，同时也有Q-1＜X-1，则根据引理1.2，上面两式变为Xq＜①和②，又由方程(1)可变形为

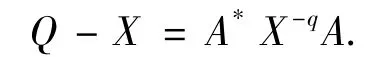
则有

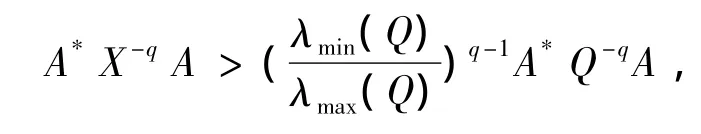
即

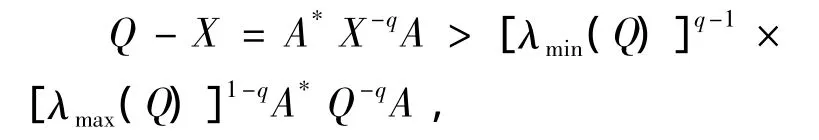
则

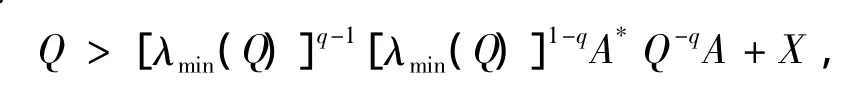
则有

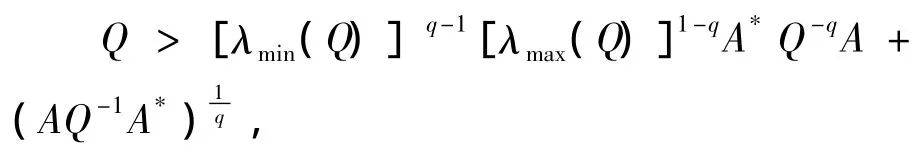
即

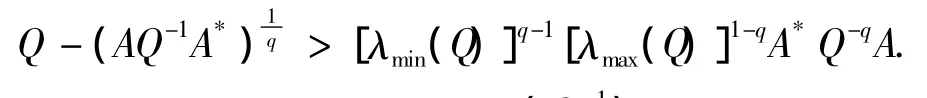
则有

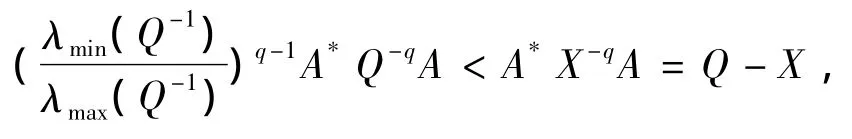
即

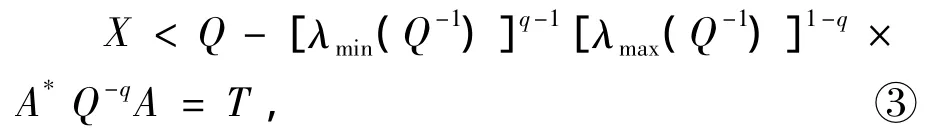
另一方面，由于方程(1)为X+A*X-qA=Q，它可变形为

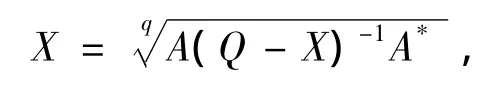
则由引理1.1可得

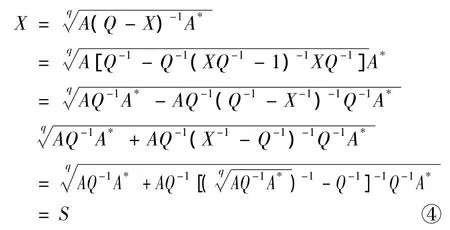
由上述的③和④，则有X∈(S，T).

注2.1 根据定理2.1可知

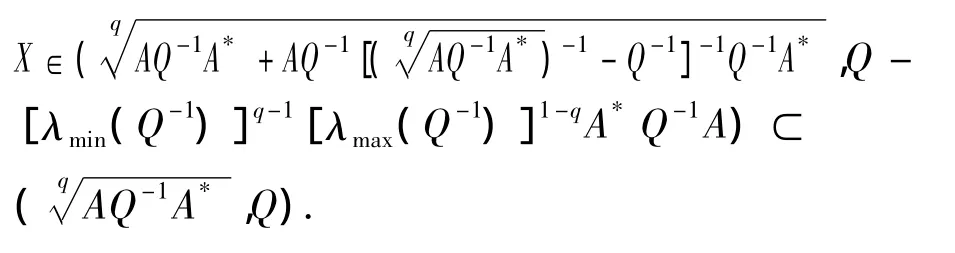
定理2.2 如果当X∈时，

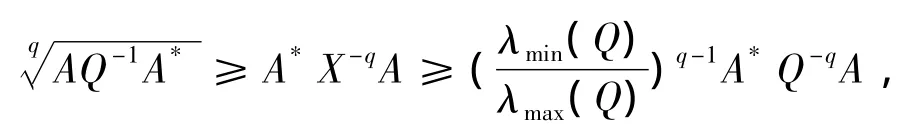
则方程(1)有正定解，且如果

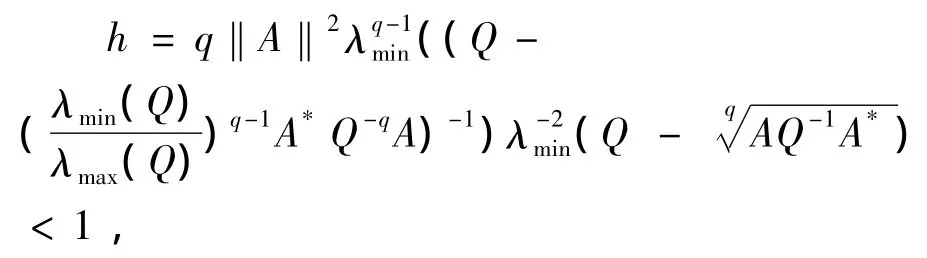
则方程(1)有唯一的正定解.

证明 考虑映射G(X)=Q-A*X-qA，且令

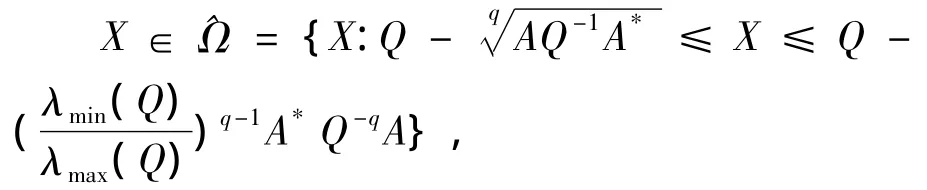
显然，是一个凸闭集且有界，并且G(X)是上的连续函数.当X∈时，有

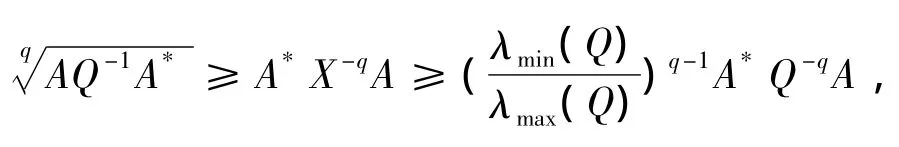
则又有

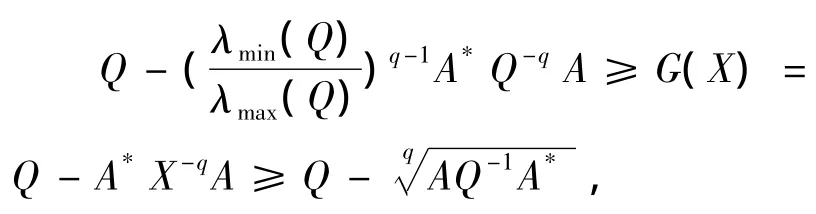
即

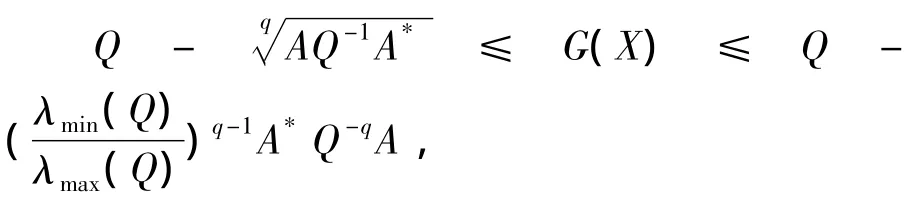
因此有G(X)⊆.

根据Brouwer不动点定理，G(X)在区间上存在不动点，且它就是方程(1)的一个解.

对于∀X1，X2∈，有

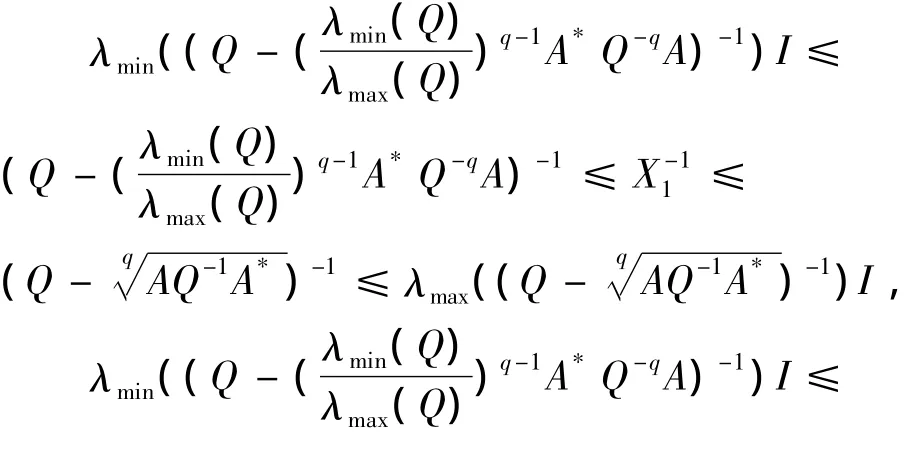
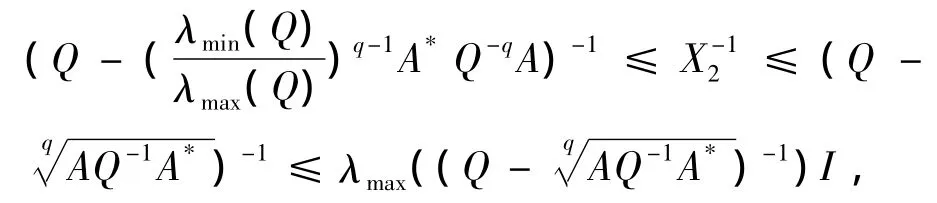
则由引理 1.3，有

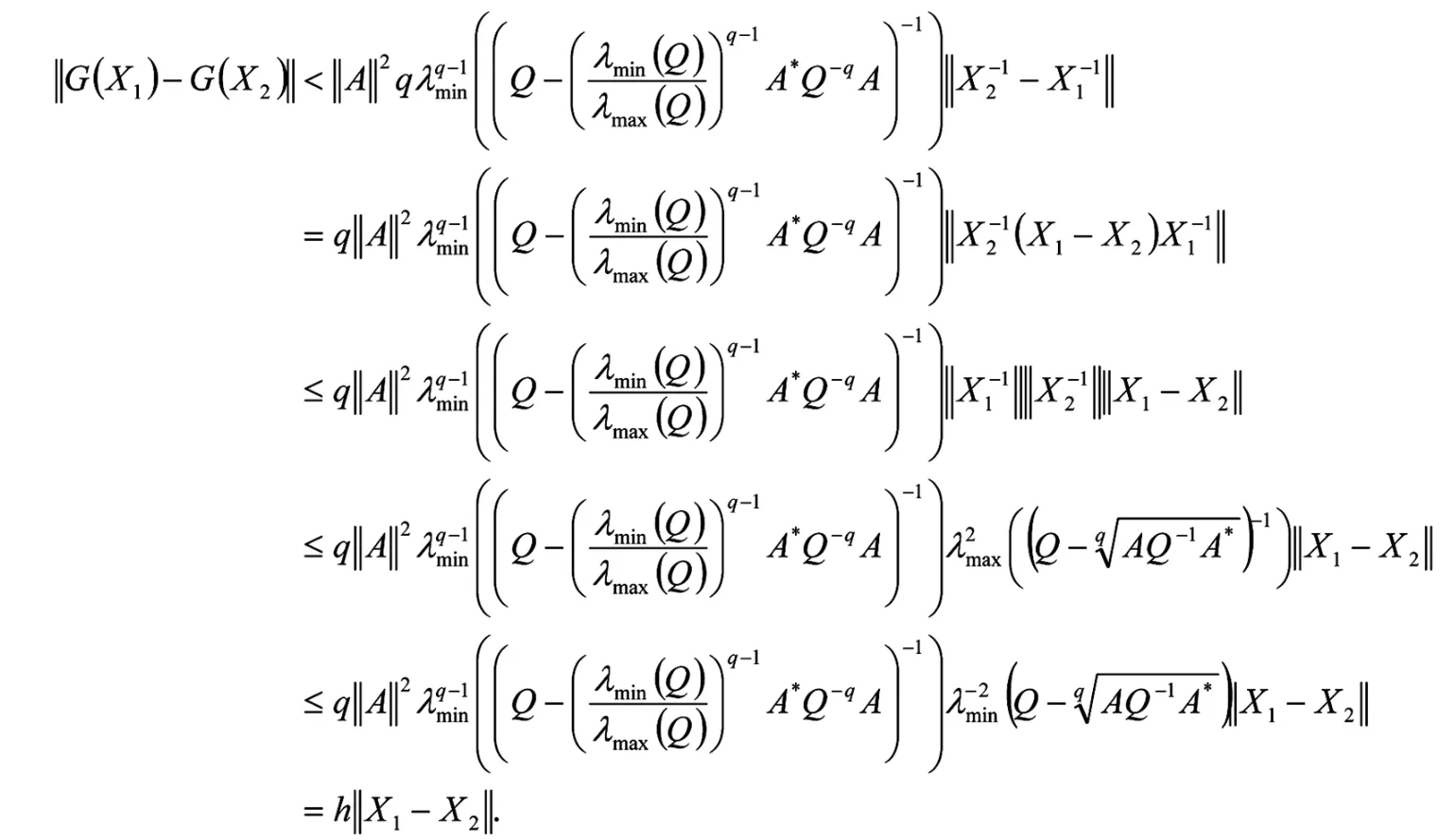
由于h＜1，所以G(X)为上的压缩算子，又由Banach的不动点定理可知G(X)在上有唯一的不动点，并且这个不动点是方程(1)的唯一正定解.

3 用迭代法求矩阵方程的正定解

在这一部分提出了求解方程(1)的迭代法和推导迭代法收敛的一个充要条件，通过考虑下面的迭代方法:

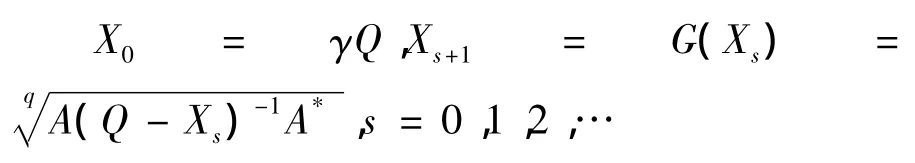
这里γ＞0.

定理3.1［8］如果方程(1)有正定解，则当时，由(1)确定的序列{xk}是单调递增并收敛于矩阵方程(1)的最小正定解Xs.

［1］ Anderson W N，Morley T D，Trapp G E.Positive solutions to.Linear Algebra Appl，1990，134:53-62.

［2］ Engwerda J C.On the existence of a positive definite solution of the matrix equatio.Linear Algebra Appl，1993，194:91-108.

［3］ Chen X，Li W.On the matrix equation:solution and perturbation analysis.Math Num Sin，2005，27:303-310.

［4］ Guo C，Lancaster P.Iterative solution of two matrix equations，Math Comput1999，68:1589-1603.

［5］ Gene H.Golub，Charles F.Van Loan，Matrix Computations，3rd ed.，The Johns Hopkins University Press，Baltimore and London，1996.

［6］ Furuta T.Operator inequalities associated with Holder-Mc-Carthy and Kantorovich inequalities.J Inequal，1998:137-148.

［7］ Bhatia R.Matrix analysis Springer，Berlin，1997.

［8］ Duan Xuefeng，Liao Anping.On the nonlinear matrix equation［J］.Mathematical and Computer Modeling，2009，49:936-945.