浅谈应用洛比达法则求不定式极限

康佳鑫

(哈尔滨师范大学)

0 引言

学习数列极限和函数极限时，遇到过无穷小(大)量之比的极限，由于这种极限可能存在，也可能不存在，所以这个问题就需要一种独特方法即洛比达法则来解决.弄清不定式极限的理论与方法是极其重要的.

1 基本概念

把两个无穷小量或两个无穷大量的比的极限统称为不定式极限，分别记作型或型的不定式极限.现在将以导数为工具研究不定式极限，这个方法通常称为洛比达法则或罗毕塔法则.

2 理论依据

定理1(洛比达法则)若函数f(x)和函数g(x)满足:

②在点x0的某空心邻域u0(x0)内两者都可导，且g'(x)≠0

定理2(洛比达法则)若函数f(x)和函数g(x)满足:

②在点x0的某空心邻域u0+(x0)内两者都可导，且g'(x)≠0，

若将以上两定理中x→x0换成，只要相应地修正条件也可得到同样的结论.此定理利用柯西中值定理来证明，在此，笔者就不一一赘述了，证明过程详见文献［1］.

3 应用时注意事项及技巧

求极限的每种方法都有其自身的优越性与局限性，在使用洛比达法则时必须注意以下几点:

注1 不能对任何比式极限都按洛比达法则来求解.首先必须注意它是不是不定式极限;其次是观察它是否满足洛比达法则的其它条件.

下面这个简单的极限

就会因右式的极限不存在而推出原式的极限不存在这个错误的结论.

注3 使用洛比达法则之后，题目应变的相对简单了，如果越变越难或者没有变化，说明该题不适此法.

那么这个极限就不适合用洛比达法则，正确做法是:

注4 如果f'，g'，f″，g″满足相应的条件，可以再次使用洛比达法则.

解:容易检验f(x)=1+cosx与g(x)=tan2x在x0=π的邻域里满足定理1的条件①和②，又因

故由洛比达法则求得

在使用洛比达法则时，如果能与其它求极限的方法有效结合运用会收到事半功倍的效果.如，结合四则运算法则，迫敛性，重要极限，等价无穷小量替换等方法.

解:利用ln(1+x2)～x2(x→0)，则得原式=

在利用洛比达法则求极限时，为使计算更加快捷减少运算中的诸多不便，可用适当的代换，简记为换元法.

4 其他类型不定式极限

(i)“0·∞”型:通常无穷大都写成无穷小的倒数形式:

(ii)“∞-∞”型:由(i)中形式知

这样就把“∞-∞”型化成“”型或“”型.

(iii)“00”“1∞”“∞0”型:对 于 幂 指 函 数，这样就把幂指函数的极限化成指数函数的极限，由于指数函数是连续函数，可以先求出指数位置函数的极限.而指数位置的函数变成“0·∞”型未定式，就回到(i)的情况了.

并应用洛比达法则得到:

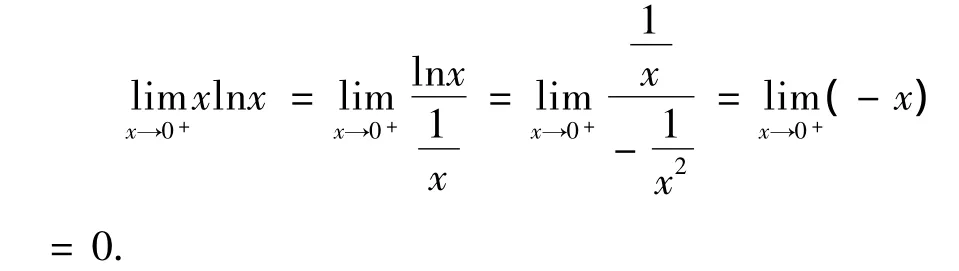
注意:此题型出现lnx，一般进行恒等变形时通常都把它放在分子上.

解 这是一个∞-∞ 型不定式极限，化简并通分后化为型的极限.

解 这是一个00型的不定式极限，按上例变形的方法，先求型的极限，

当k=0时上面的结果仍成立.

解 这是一个1∞型的不定式极限，作恒等变形

解 这是一个∞0型的不定式极限，类似地，先求其对数的极限型)

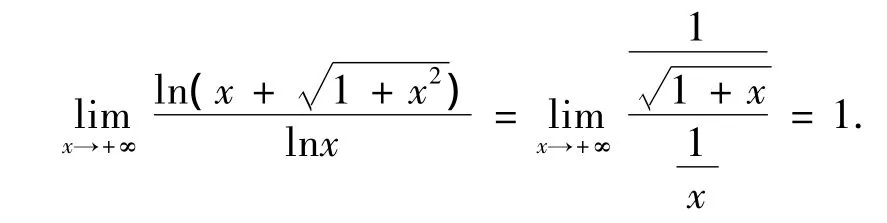
最后指出，对于数列的不定式极限，可利用函数极限的归结原则，通过先求相应形式的函数极限而得到结果.

使用洛比达法则必须要强调的是:

(1)每次在使用洛比达法则之前，务必考查它是否属于不定式极限，否则不能用.

(2)一旦用洛比达法则算不出结果，不等于极限不存在.

(3)应用洛比达法则求极限时，经常与结合求极限的其它方法使用.

5 复平面上的推广

复变函数中的一些概念和结论都是实函数中相应概念的推广，那么对实变函数中“不定式”的分析可以利用洛比达法则，那么对复变函数中的“不定式”是否有相应的洛比达法则?答案是肯定的.现将复变函数中的洛比达法则简单归结如下，留给读者体会与思考:

定理3(洛比达法则)若f(z)与g(z)在点z0解析，且f(z0)=g(z0)=0，g(z0)≠0，则

注意:洛比达法则推广到复平面上是成立的，但条件与实数集中洛比达法则的条件有变化.利用给出的洛比达法则可以更方便的求解复变函数的某些类型极限以及判定解析函数孤立奇点的类型等问题.

洛比达法则这个方法是在数学分析里求解不定式极限的重要方法.在做求解极限的题目时，仅仅掌握这个方法是不够的，极限计算的方法灵活多样，但也具有一定的规律性，只要掌握好极限理论，多做练习就能够得到一些解题的规律，增强解题的能力.但做题时必须要细心分析仔细甄选，选择出适当的方法.这样不仅准确率更高，而且会省去许多不必要的麻烦，起到事半功倍的效果.这就要求学习者要吃透其精髓，明了其道理，体会出做题的窍门.达到这样的境界非一日之功，必须要多做题善于总结，日积月累，定会熟能生巧，在做题时得心应手.

［1］ 华东师范大学数学系.数学分析:上册第四版［M］.北京:高等教育出版社.

［2］ 张天德，韩振来.数学分析辅导及习题精解［M］.延吉:延边大学出版社，2011.7.

［3］ 裴礼文.数学分析中的典型问题与方法:第二版［M］.北京:高等教育出版社，2006(4).

［4］ 钟玉泉.复变函数论:第三版［M］.北京:高等教育出版社.