丰富视觉体验 优化观察效果

朱宇

《义务教育数学课程标准（2011年版）》中明确指出：“学生应当有足够的时间和空间经历观察、实验……等活动过程。”数学学习是从感性认识开始的，学生通过以观察为主要形式的视觉活动对学习素材进行多层面、多角度、多维度的观察、比较、选择与归纳，生成视觉体验。

由此可知，视觉体验是建立在积极观察基础上的归纳与整合，是通过某种特殊的抽象过程而生成的经验。然而，很多情况下，学生只见表面而不及其里，只关注个别而忽略整体，目之所及却思维缺席……对此，教师不应简单归因为“学生不认真、不细致”，而应该从视觉体验形成的机理出发，寻找改善学生视觉体验的具体办法，提高数学观察活动的效果。

一、激活视觉意趣

真正的视觉体验，起步于对物象中形式因素的观察，发现物象中的疑惑之处或趣味之点。简单地说，观察是为了有所发现，随意进入视网膜里的事物多半与观察无关。

如在“7的乘法口诀”的巩固练习环节，教师设计了“比一比，谁的眼力准”的游戏（如图1）。课件呈现“小猪吹泡泡”的场景，泡泡上杂乱出示7的乘法口诀中的6句，要求学生在短时间里找出少了哪句口诀的得数。

学生聚精会神，仔细观察，比对口诀，“找到了！找到了！”找到的学生欣喜若狂。随后，课件又变换出示6个积，让学生寻找缺少的一个积。游戏进行了4次，学生仍觉意犹未尽。枯燥乏味的口诀背诵变身为兴趣盎然的“寻宝游戏”，无需提醒学生“仔细看”， 新颖别致的设计让学生的视线高度聚焦。

图1

又如在“找规律”一课的教学时，教师安排了一场比赛：在3秒钟内迅速记住一长串数字，男生记“162536496481”，女生记“123412341234”。结果，男生组落败，“不公平”的抗议声表明，他们对两组数据进行了观察比较：第二组数据太有规律了！课尾，教师引导学生再次观察第一组数据，学生终于参透玄机：“162536496481”的规律是“16，25，36，49，64，81”。原来规律藏在这儿！

在上面的两个片段中，蕴含数学任务的情境给学生带来了刺激，他们感受到新奇，思维也发生了冲突，产生一种认知和情感方面的需要，进而产生了属于自己的真实问题，促使他们主动地观察，视觉体验真实地开始了。需要注意的是，如果仅仅是形式上的新奇，只能吸引学生外在的短时兴趣。教师既要促进学生外在动机向内在动机的转化，也要推动学生对情境的外在兴趣与数学思维活动的内在兴趣紧密结合，从而赋予视觉体验以“数学”特征。

二、过滤视觉行为

用眼睛看，是容易的，但要透过现象，有所发现是困难的。观察不仅需要眼睛的凝视，更需要心的凝视。观察活动的全过程包括初步感受情境，观察、发现并分析数学问题，每一个环节都会带给学生不同的体验、感受和发现。为了确保学生能生成或积累必要的数学观察经验，就必须对视觉行为进行有意识的引导与选择。

例如，在“折线统计图”的教学中，我们发现，学生在观察条形和折线两种统计图的基础上，能说出“折线统计图不但能表示数量的多少，而且能反映数量增减变化的情况”，但是对两种统计图各自特点的解读却很苍白，尤其是不清楚怎样根据数据特点合理选择呈现方式。

浙江名师俞正强老师在 “折线统计图”一课教学时采用的方法值得我们借鉴。俞老师先出示“上海月平均气温”条形统计图，学生观察之后，把能看到的都表达了，可俞老师还在追问：还能看到什么呢？“逼”着学生“过滤”掉其他非本质信息，转向研究哪两个月之间温差比较大，大了几度，从而体会到折线统计图产生的合理性和必要性。接着，课件动态演示条形统计图变化为折线统计图的过程。审视两种统计图，借“主角”这个拟人化的形象，学生感悟到条形统计图上，1月份一个主角，2月份一个主角，3月份一个主角……12个主角各走1个月，而折线统计图12个月只有一个主角。舍弃其他非本质信息，聚焦“主角”的“行走轨迹”，学生悟出了根据数据特点合理选择呈现方式的关键——看看有几个主角。这样的加工，不仅帮助学生深刻理解了折线统计图的价值和意义，而且为下一步理解条形统计图的“离散”和折线统计图的“联结”埋下伏笔。

更为常见的是在数学主题图的观察环节，如果不引导学生对视觉行为进行过滤取舍，那么丰富的信息资源就容易把学生引入误区，费时费力。所以，出示主题图后，教师不妨这样一问：“同学们，请认真看图，然后告诉大家你在这幅图上发现了哪些数学信息？”最后根据学生的回答教师引导归纳，选择合适问题，让学生去探究解决。

三、关注视觉理解

经过观察阶段获得的数学感性经验，很大程度上仅是一些同某些实物、图形、操作情境紧密相关的具象，教师还需要据此进行适时适度的抽象，实现感性经验的提升。

例如，在“长方体的认识”教学中，在发现棱的特征的过程中，教师基于观察、超越观察，多次引导学生进行直观图形或实践操作基础上的观察活动、想象活动、推理活动，学生在直观的基础上不断产生新的思考。对学生的思考来说，直观的形式、视角越多样，积累的表象就越丰富，也就越容易达成数学抽象，越容易实现数学理解。而在接下来探究“面”的特征环节，教师反其道而行之，不再像发现棱的特征那样先观察再思考，而是先思考再观察。

课件先出示一个长方体的长、宽、高（如图2），接着出示6个图形（9×9，9×7，9×4，6×6，6×4，4×4），要求学生判别能否从中找到这个长方体的6个面。学生此时观察到的是长方体“棱”的特征，教师的要求是“从棱联想到面”，因为有前面实践活动形成的表象支撑，学生很有条理地说出“因为前面的长是9厘米，宽是4厘米，和9×4的长方形图是一样的”。值得一提的是，教师虽然给出了6个图形，但是其中并没有上、下两个面，需要学生去伪存真，在脑海中鉴别、想象、构图，这进一步拓展了学生的想象空间。推理结束后，教师出示长方体的直观图，组织学生共同经历想象后的验证活动，概括出长方体面的特征。

再如，在“倍的认识”教学中，课件只出示“12朵黄花”，但却没有红花，只出现一种量，这就让见惯了“两种量”的视觉出现了真空。这时，教师提问：我们再来看看，黄花的朵数是红花的几倍呢？学生感觉有困难，感叹“1份红花有几朵太关键了！”。随后，教师组织学生“猜一猜”：如果红花有3朵，黄花的朵数是红花的几倍呢？如果1份红花有4朵、6朵，它们之间的倍数关系又会是怎样呢？学生先是在纸上圈，渐渐地，教师提出“在自己的脑海里默默地圈一圈”。教师最后的发问画龙点睛：“孩子们，黄花一直是12朵，那为什么两种花之间的倍数关系在发生变化呢？”

所谓视觉，是眼中之像经过感知、选择、分析后形成的某种形式语言的体验状态，不只是客观事物的映像，还包括对事物的假设、推理与理解。所以如以上两个片段一样，需要呈现变化的情境，让视觉摆脱操作性情境的单纯刺激，从与活动相当的概念水平上升为抽象理解的水平。

四、完善视觉表达

课堂上，教师还需要组织学生对视觉感知内容进行反思和交流，及时概括所获得的经验并进行形式化的表述，使已得经验条理化和系统化。

还是以“倍的认识”教学为例，教师引导学生将2朵蓝花，6朵黄花“圈一圈”，在此基础上，直观形成对倍的初步认识：蓝花有2朵，黄花有3个2朵，我们就说黄花的朵数是蓝花的3倍。接下来，出示蓝花2朵，黄花12朵。教师提问：现在黄花的朵数是蓝花的几倍呢？能用圈一圈的方法解决吗？学生汇报之后，教师设疑：观察刚才的两幅图，你们是怎么一眼就从图中看出第一幅图中黄花是蓝花的3倍，而第2幅图中黄花是蓝花的6倍的？

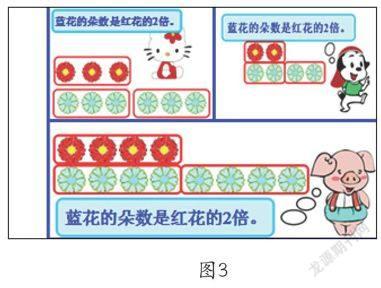
学生由“几个几”的实物顺利过渡形式化“倍”的概念：能圈出这样的几份，就是一份数的几倍。然而，这样的视觉注意还只是因教师的提醒而被动地注意，并不是为某种目的寻找特定目标而有指向的选择。所以，接下来，教师组织学生在比较中充实对倍的认识，掌握倍的内涵。先出示一组图，都表示“蓝花的朵数是红花的2倍”（如图3）。组图的数量变复杂了，学生需要在复杂的环境中找到“特殊”的对象——关于“2倍”背后的共同规律。学生就需要对观察到的图意进行类比加工，寻找共性，准确表达。

图3

接着，出示图4，质疑：你觉得下面的哪幅图能够表示“蓝花的朵数是红花的几倍”呢？蓝花的朵数是红花的3倍、还是2倍呢？提供反例为的是让学生在观察中比较和思辨，使学生认识到黄花不是随意圈的，要根据蓝花的朵数来圈，从而加深对“倍”的理解，将一般意义上的“看”生成了具有数学特点的视觉语言。

图4

需要注意的是，不同学生语言表达的能力水平是不一样的。如果时间仓促，只有少数学生完成了观察任务，教师就立即组织反馈评价，大多数学生就不能获得较为充足的观察体验。另外，在交流观察所得的环节，还必须关注学生参与机会的公平性，让学生畅所欲言，通过互动交流完善观察体验。

视觉不只是一种与感觉、知觉有关的生理与心理现象，它其实更是一种特殊的思维方式，与选择、判断、整合等智力活动密切相关。课堂上关注学生视觉体验的完善，有助于学生获得丰富而深刻的数学活动经验，学会从数学角度去观察周围的世界，让数学课堂的有效教学真正落到实处。

（江苏省高邮市天山实验小学   225600）