这道习题，学生为啥不肯一一列举？

毛蓉 严育洪

【“望”：病例观察】

这节课是苏教版五年级上册“解决问题的策略”——

出示例题（如下图）。

教师先让学生随意列举，在巡视中，选择展示有遗漏的学生作品，引导学生有序列举。然后，教师让学生在下发的一张5格空表中一一列举。反馈时，教师选择从长为10米开始列举的学生进行展示（如下表1），而笔者看到，许多学生是从长为1米开始列举的（如下表2）。

表1                                   表2

新授结束，教学进入练习环节，当屏幕上出示教材安排的这样一道习题时（如下图）。

不知道是因为疏忽还是执教教师认为不重要，竟然漏打了习题后面括号里的要求——先填表，再回答。

在学生埋头列举中，教师发现平时表现不错的一位女生却不动笔，呆坐着，教师关切地询问原委：“你怎么了？是不是身体不舒服？”谁知这位女生委屈地站起来说：“这道题，不是以前学过的一一搭配么？只需要3×4=12就可以很快地算出来了！”同学们一阵骚动，教师愕然，呆了一会，猛然发现自己少打了习题要求，急忙补上后说：“注意：教材要求一一列举！”这位女生噘着嘴怏怏坐下……

【“问”：病历记录】

课后，笔者找来三个学生作为代表进行了交流。

首先问从1开始列举的学生：“你是怎么想到从1开始列举的？”

他答道：“探索问题的时候，不是从最小的开始研究么？”

接着问从10开始列举的学生：“你是怎么想到直接从10开始列举的？”

他挠着头不好意思地说道：“书上看到的。”

最后问那个用乘法计算的女生：“你为什么选择用乘法计算呢？”

她振振有词：“这道题要求‘一共有多少种不同的搭配’，用一一列举反而麻烦啊！”

……

问完学生，笔者转而问上课教师两个问题：

一是“对学生作品，你为什么选择性展示？”

上课教师理由充足：“从10开始列举，这是教材写着的。何况‘长=1，宽=10’，这种说法多别扭啊！所以教材上要从长到短来列举。”

二是“对学生意见，你为什么消极性处理？”

上课教师有些心虚：“用一一列举的策略解决问题，这是教材要求的。只不过我忘了打上题目要求了。”

……

【“切”：病理诊治】

本节课的教学目标是使学生经历用一一列举策略解决实际问题的过程，能通过有序列举找到符合要求的答案，感受到一一列举的特点和价值，进一步发展思维的条理性和严密性，培养列举能力，发展列举技巧。

在备课时，我们需要注意的是，这一教学内容被安排在五年级的教材中，所以在教学方式的选择上，教师应充分考虑学生“已有了什么”。对照上述教学片段，不难发现教师的“要”与学生的“有”之间至少存在着以下三大问题。

问题一：在教学例题时，教师大多循着条件到问题的路线开始一一“列举”出各个知识点、思维点以及注意点：首先由条件“1米长的栅栏”，让学生注意所取数据应为整数，然后由条件“22根1米长的栅栏”，让学生想到围成的长方形周长为22米，最后由问题“面积最大”，让学生知道最后比的是面积，并知道面积在发生着变化。

根据五年级学生的思维特点，在指导解决问题的策略时，教师的教学要求应更多地侧重“执果索因”的分析法。也就是对本节课的例题，可以让学生从条件想起，但更应看重从问题想起，由“面积”让学生想到决定长方形面积的两个要素“长”和“宽”，从而在周长不变的情况下，一一列举出长和宽的相应变化来求出面积的变化。

问题二：在教学例题时，许多教师会像课例那样，先让学生随意列举，然后寻找一些无序列举的学生作品进行展示，引导学生有序列举。其实，有序思想在学生之前的学习活动中（例如从低年级的“认数”到刚学不久的“因数和倍数”）无时无处不在，并非是“新知识”。众多知识都或隐或现地反映着有序思想，可以说，有序性是数学学科的特征之一，也是数学研究的方法之一。所以，本课教学时，笔者认为，教师不妨基于学生的“已有”直接指明方向：“当列举比较多的围法时，我们怎样可以做到不重复、不遗漏？”引导学生自觉调用经验，直接进行有序列举。笔者认为，给方向比给方法重要，因为有了方向，就有了方法。

如此，学生的学习也就不会被教师牵着走，也就不会出现本课教学中教师对学生的“强求”——必须像教材上那样从10开始列举，而会尊重学生的原始思维，从最小开始一一列举，例如假设长为1米，通过（22-1×2）÷2求出宽为10米……至于教师担心的——“‘长=1，宽=10’这种说法多别扭啊！”，其实无需担心，因为“长”与“宽”是相对而言的，“长”未必要长。如果学生产生质疑，教师可以就此解释，当然也可以以长边为“长”，此时只需把“长”改成“宽”即可，由此可见，这并不是“教材上从长到短来列举”的根本原因。

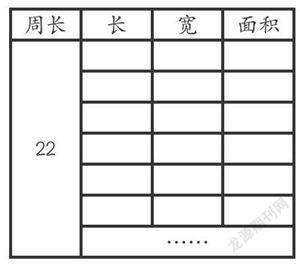
在发给学生用于一一列举的表格中，教师不妨改变教材所示样式，增设“周长”一栏（如下表）来记录学生的思考过程和思考结果，这样更有助于学生从“不变”中去列举出“变”。在反馈时，教师再引导学生采用另一种思路22÷2=11，然后通过11的分成来一一列举，这样就可以转接到教材从10开始列举这一思路。

学生顺着原始思维，从小到大列举到5的时候，自己会发现接下去就会出现重复，从而自动停止列举。由此观察上述课例，教师也并没有给学生解释为什么只列举到6的原因。另外，教师发给学生正好有5格的表格让学生填空的做法，明显有着暗示性和包办性（教师并没有站在学生立场，学生列举前怎么就知道只有5种情况呢？）。正确的做法是：表格的格数不应该恰到好处，要么多几格，要么少几格，或者干脆没有格子，让学生有一种情况画一个格子。

问题三：也就是本文标题所反映的问题——“这道习题，学生为啥不肯一一列举？”从教学现场可以看出，上课教师在备课时根本没有想到这样的题目学生以前在学习“搭配规律”时已经有过。有些学生触景生情，会勾起对往事的回忆，从而发现用原有方法“3×4=12（种）”解决问题更容易。

教材上在这道习题问题之后的括号中注明了要求——“先填表，再回答”，由此可以看出教材意图是让学生“拿着新船票登上旧客船”，用新学知识解决老问题，体会之前学的“一一搭配”与今天学的“一一列举”方法之间的联系。然而，遗憾的是，教师不懂编者的心，在出示这道习题时一不小心漏掉了括号中并非可有可无的附带要求，结果就出现了课中那位女生的“不配合”和“不买账”。出现这种状况，不能怪学生不懂教师的心，课例中教师强行把学生拉回教材的处理方式，恰恰暴露出教师不懂学生的心。如果教师具有策略意识和战略眼光，就会趁机借题发挥，抓住学生真实的学习反应，肯定学生的想法，并引导学生进行比较，明白“用一种特定的策略解决问题，并非总是最优的”这样一种辩证思想，从而提升教学境界，为全课添上精彩一笔。

然而，在现实教学中，这节课，教师大多只想到策略的优越性，而想不到策略的局限性。如果想到了，也抱着“多一事不如少一事”的心理，不愿意去捅破，这样只会造成学生认识的不全面甚至不正确。有意思的是，课例中教师的疏忽，却换来了这样的契机，可惜没有能够“因祸得福”，造福于学生，让这一生成资源没了意思。

如果没有教师的疏忽，也没有学生的质疑，对这道习题，教师可以有两种处理方式：一是完整出示习题要求，让学生必须使用新方法数出种数，然后再比较和沟通新（一一列举）旧（一一搭配）方法之间的联系，从而明白也可以用旧方法直接算出种数;二是把习题原来的问题“一共有多少种不同的搭配？”改成“有哪几种不同的搭配？”，迫使学生只能运用新方法解决问题，把结果一一列举出来。

好的教学应该能够瞻前顾后。我们除了可以利用教材这一道习题“向前（已经学过的知识）看”，让学生看到用一一列举策略解决问题可能存在的局限性，我们还可以利用教材另一道习题（如下图）“向后（还没学过的知识）看”，在学生用一一列举策略解决问题之后，顺便把题目中的天数加大，让学生体会到一一列举的麻烦，在此教师可适时告诉学生：“以后学了最小公倍数知识，不用一一列举，就可以轻松算出结果。” 如此，学生的认识才会不断“进步”，并最终明白：随着知识的不断“进步”，解决问题的方法也会不断“进步”。并逐步形成这样的策略意识和策略判断：首先考虑“能不能”（用一一列举策略解决问题），然后考虑“要不要”（用一一列举策略解决问题）。

任何一个人在面对像例题那样“变化着”的问题时，在没有找到新办法或获得好办法之前，首先想到的就是一一列举这种“笨办法”。但我们并不能因此而否定一一列举作为解决问题策略的作用，因为在特定情境中，例如在面对教材的又一道习题（如下图）时，这种“笨办法”可能是解决问题的好办法。

总之，不管有没有像课例中那样的生成，我们都应该通过本节课让学生形成这样的认识：策略是活的。而要达到这一教学境界，教师就必须把策略教活。

（江苏省无锡市硕放实验小学   214142

江苏省无锡市锡山教师进修学校   214101）