小学数学教材要厘清逻辑顺序

张奠宙

平行和平移，都是小学数学中的几何学名词。二者之间存在着内在的逻辑顺序，即先有平行，才有平移。小学数学尽管需要深入浅出，却不宜违背这一逻辑顺序。

让我们看某现行教材中关于平行直线的定义。

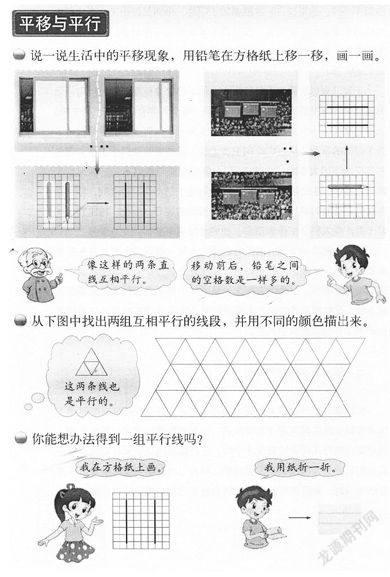
这一段教材，通过移动的门窗、上升的国旗，以及铅笔的水平移动的观察，就说“像这样的两条直线互相平行”。显然，这是从物体的平移，给直线的平行作定义式的陈述。这样处理，会出现不少问题。

首先，门窗、国旗都是立体或平面的实体，抽象之后，乃是二维的平面，怎样和一维的“直线”联系起来呢？像国旗升起的画面中，平行线在哪里？不加以明确指出，让学生如何理解编写意图？

其次，若从两支铅笔抽象为几何图形，不过是一条线段，怎能说是直线呢？线段和其所在的直线，需要有所区分。这里的断语，应该是“像这样的两条线段互相平行”。至于说这也是它们所在的两条直线互相平行，那是另一种约定，在界定一个对象时要分清楚，不能混同起来。

第三，最为严重的混淆是用平移来界定平行，把二者的逻辑顺序弄颠倒了。说到底，究竟是先有“平行”，还是先有“平移”呢？

先来看什么是平移。百度词典这样定义：

“在平面内，将一个图形上的所有点都按照某个方向作相同距离的移动，这样的图形运动叫作图形的平移运动，简称平移。”

这里的一个关键词是“所有点按同一个方向”，它的意义就是每组对应点连成的直线都彼此平行。这就是说，教材图上那支平移的铅笔，其上的每个点都要沿“水平方向”移动一个固定的距离。如果将铅笔头移动前后两点的连线线段（记为ab），铅笔底部点前后形成的两点连线（记为cd）那么因为是同一方向，所以必须有ab∥cd。这时，abcd四点构成一个矩形。进一步，那支铅笔也可以沿45度角向“东北”方向平移，铅笔各点扫过的图像就是一个平行四边形。

这就是说，作平移运动时，图形中无限多的点都要保持“同一方向”，也就是要形成无限多条的平行线。因此，先有平行概念和平行判断准则，才能作平移运动。用平移定义平行，在逻辑上有误，混而有错。

在这页教材上，还可能会产生另外一些误解。

1.以为可以用两条线段彼此间是否为平移来判断是否平行。但这是做不到的。事实上，判断两线段是不是平移，必须把平移的那个“统一方向”找出来。为了找这个方向，最后不得不依赖同位角相等的那些平行线判定法则。因此，想用平移概念，绕开平行线的严格定义和判别准则是做不到的。

2.教材的那两支铅笔，是向水平方向和垂直方向平移。容易产生的错觉是，平移就是水平方向的移动，或者是垂直方向的移动。这就会造成平行线都是水平的或垂直的错误印象。

3.教材呈现的平移操作，只能在方格纸上向水平或垂直两个方向移动。 那么，要在方格纸上作45度、60度方向的移动怎么办？教材没有交代，也无法说清楚。

综上所述，用线段平移来界定线段平行， 在逻辑上有误，既不能实际操作，又会带来一些误解，应予修正改进。

笔者认为，平行线教学要和“方向”概念联系起来，用直线的方向相同来定义直线的平行，即用直观的、相当于同位角判定准则的情境来进行处理，那要另文探讨了。

（华东师范大学数学系   200241）