实施分层练习 感受数学魅力

叶婉红

如何针对“三角形内角和”的相关知识上好一节练习课，这一问题在以往的教学中并没有引起教师们的关注。因而在平常的练习设计时，比较常见的是重复已知三角形两个角的度数求第三个角的度数的题目，练习形式比较单一，难以引发学生的学习兴趣。因此笔者针对这一内容作了深入的思考，主要通过对数学内涵的挖掘，对练习内容作了一定的拓展。现把教学的简要过程整理如下，供大家参考。

【教学实录】

一、基本练习

（一）判断：下面三个角有可能是同一个三角形的三个内角吗？

①  70°、60°、 50°    （     ）

②  65°、65°、 50°    （     ）

③  37°、53°、100°  （     ）

④  90°、40°、 50°    （     ）

学生针对以上每组三个角的度数，判断出第①、②、④组的三个角的度数相加都刚好是180°，所以都有可能是同一个三角形的三个内角。教师在学生判断的同时，引导学生发现第②组的三角形是一个等腰三角形，第④组的三角形是一个直角三角形。

接着教师又提问：如果一个三角形的三个内角刚好是第④组的90°、40°、50°，你能画出这个三角形吗？

学生根据以上的度数画出相应的直角三角形，这时教师从学生所画的三角形中找出了两个大小不同的直角三角形，利用投影呈现在屏幕上，并提问：为什么会出现大小不一样的三角形呢？

生：它们的边的长短不一样。

师：也就是说两个三角形虽然三个角分别相等，但有可能什么不一样？

生：有可能大小不一样，也就是有可能边的长度不一样。

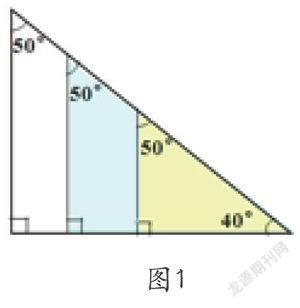
教师借助于投影把两个大小不同的直角三角形按其中的40°角重叠在一起，接着再把一条直角边进行左右平移，与斜边和另一条直角边相交出多个直角三角形（如图1），并提问：你们看到了这些三角形什么变了？什么没有变？

图1

生：三角形的大小变了，三角形三个内角的度数没有变。

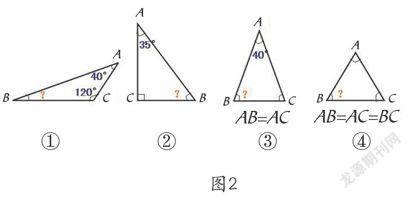
（二）分别算出以下三角形∠B的度数（如图②）

学生独立列式计算之后，教师组织反馈评讲。对第②、③、④小题，引导学生根据三角形的特点交流计算方法。

图2

（评析：运用“三角形内角和”的知识对四组角进行判断，使学生较快地回忆起基础知识。而在这一环节中值得我们关注的是，教师让学生针对已知直角三角形的内角度数画出这个三角形。看似是一个画图操作，实际上引出了对此后要学习的“相似三角形”知识的初步思考。学生在这样的画图、观察、比较中，逐步知道三个内角虽然分别相等，而它们的大小可以不同。再通过投影的展示，初步感受到三条边是在同时相应缩短或延长的，这也是之后要掌握的相似三角形中对应边成比例的知识。之后关于求出指定角的度数的练习，则让学生再一次巩固了三角形角的相关知识，及不同类型三角形角度的计算方法。）

二、拓展练习

（一）用三角形内角和研究它的外角

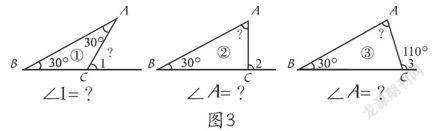
投影出示问题一：用三角形内角和研究它的外角。（同时呈现下图3）

图3

师：如图中的∠1、∠2、∠3都是从三角形的一条边延长，并与另一条邻边所夹的角，都叫作这个三角形的一个外角。请同学们根据下面要求完成学习。

① 分别求出以上每个图形中指定角的度数。

② 观察上面三个图形，你有什么发现吗？分小组互相说一说。

学生经过独立思考、计算，小组交流后，教师再组织反馈评价。在评价中发现大部分学生都能按以下的方法进行计算，教师根据学生的回答板书出每一个图的算式：

第①个图先计算∠1的邻角度数“180°-30°-30°=120°”;再用平角减去邻角得到“∠1=180°-120°=60°”。

第②个图直接看出∠2是直角，所以它的邻角是90°，∠A=90°-30°=60°。

第③个图先计算∠3的邻角“180°-110°=70°”，再计算：∠A=180°-30°-70°=80°。

当教师组织学生反馈了以上的计算过程后，一部分学生提出：我们发现了每个外角都刚好是它不相邻的两个内角的和。

师：是吗？大家仔细看一看是这样的吗？

学生再次观察片刻后，给出了肯定的答复。

此时，教师再借助于投影在第①个图上点击C点，使它在BC的边或边的延长线上从左往右移动（其他两个顶点不动），使学生直观地感受到它的外角从小变大，而三角形的另一个内角也跟着从大变小。

（评析：显然教者设计这样的外角题目，其目的是通过外角与邻角的思考，不仅进一步巩固三角形内角和的知识，而且更重要的是让学生自己去发现三角形的一个外角等于它不相邻的两个内角之和。当然对于这一结论的掌握并不重要，重要的是学生经历了观察、发现的过程，借此来提高学生发现问题、解决问题的能力。）

（二）用三角形内角和研究多边形的内角和

师：刚才大家运用三角形内角和研究了三角形的外角问题，下面我们再来运用三角形内角和研究多边形的内角和。

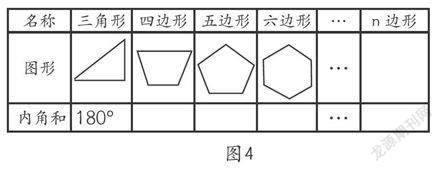
投影出示问题二：用三角形内角和研究多边形的内角和。（出示图4）

图4

同时出示以下学习要求：

① 想一想以上各图有几个内角？

② 请你用画一画、算一算的方法求出各图形的内角和是多少？

③ 想一想计算多边形内角和有什么计算规律吗？

④ 在小组内说说你的想法。

在学生通过独立思考、计算，小组交流讨论后，再组织反馈评价：

四边形分成两个三角形，它的内角和是：2×180°=360°。

五边形分成三个三角形，它的内角和是：3×180°=540°。

六边形分成四个三角形，它的内角和是：4×180°=720°。

……

师：在分法上要注意从一个顶点出发，把多边形分成几个三角形（在图4中呈现出分法）。你们发现有怎样的计算规律了吗？

学生通过以上的类推，得出“n边形”的内角和是“（n-2）×180°”的计算规律。

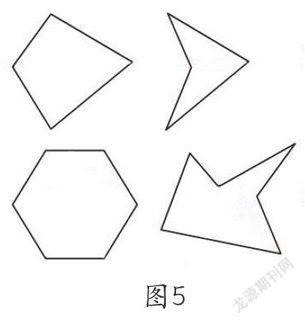
接着教师又出示了以下的凸四边形和凹四边形、凸五边形和凹五边形（如图5），并提出：请大家继续观察，它们的内角和是否还可以用以上的计算方法计算呢？

图5

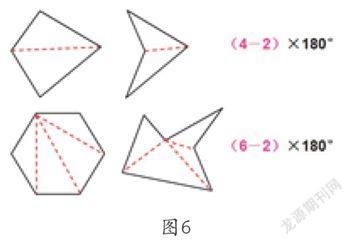
在学生的互动交流中，教师呈现图中的分法，使学生知道这里的凹四边形和凹五边形的内角和仍然可以用这种计算方法得出内角和（如图6），就是在分割时要注意一般从凹进去的顶点出发去分割三角形。

图6

接着教师继续提出：是否所有的凹多边形都可以用这种方法来计算内角和？

引导学生到课外继续思考、探究。

（评析：设计这样一组多边形让学生去研究它们的内角和，其主要目的是让学生去经历观察、尝试、操作、发现计算规律的过程，从中使学生获得一定的数学基本活动经验。学生在找到凸多边形的分法之后，得出内角和的计算规律难度并不大。而叶老师不仅只满足凸多边形的内角和，还联想到了凹多边形。但针对一些凹多边形在分割成三角形时，在方法上是有一定技巧的，所以叶老师并没有过多地展开，只是提到：所有凹多边形是否都可以用这种计算方法？一句发问激发了学生课外的探究欲望。）

（三）用三角形内角和研究内角的变化

1. 研究顶角的变化。

师：我们现在知道无论三角形怎样变化，它的内角和始终是180°。请大家观察下面这个直角三角形（出示图7）。

图7

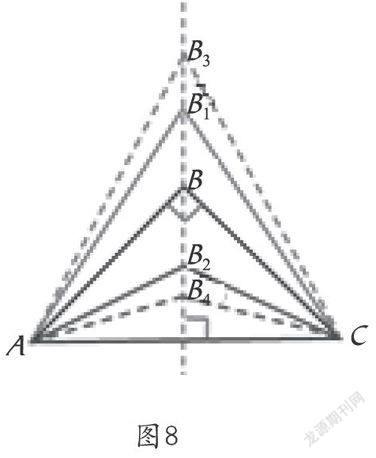
师：现在把顶角的顶点沿着高的沿长线向上移动，形成了三角形AB1C;再沿着高向下移动， 形成了三角形AB2C（如图8）。请根据下面学习要求思考：

图8

观察三角形AB1C和三角形AB2C，它们与三角形ABC的内角比较发生了怎样的变化？变化后的两个三角形分别变成了什么三角形？

学生经过独立思考、小组互动交流后，教师再组织学生反馈评价：

生1：三角形AB1C的顶角变小了，小于90°，而它的两个底角变大了。这个三角形变成了锐角三角形。

生2：三角形AB2C与三角形ABC相比，它的顶角变大了，大于90°;而它的两个底角变小了。这个三角形变成了钝角三角形。

师：你们想象一下，如果顶角的顶点继续在这条高所在的直线上作上下移动，三角形的顶角和底角会有怎样的变化规律？

等学生想象片刻后，教师在投影上继续拉动三角形的顶角，使学生直观地感受到越往上移动，顶角越小;越往下移动，顶角越大。

2.研究与圆有关的三角形内角的变化。

师：刚才我们研究了三角形一个顶角在它高所在的直线上移动，如果把它的顶角的顶点放在一条圆弧上移动又会是怎样的呢？

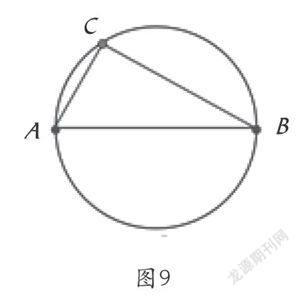
教师利用投影先出示一个圆，再画上一条线段AB把圆分成两个半圆（四年级学生只是初步认识圆）。接着引导学生在圆弧上任意确定一点C，并把C点与线段两个端点A、B连结成一个三角形（如图9），并提出：这样连结成的三角形又会是什么三角形呢？

图9

学生在练习纸上，按以上要求画三角形。当学生检验出这个三角形是直角三角形时，教师又趁机提出：在圆弧上再任意多找几个点，把每一点分别用同样的方法与点A、B连结起来形成三角形，这些三角形还是直角三角形吗？

学生认真地操作着，过了一段时间后，学生兴奋地得出：无论圆弧上的点如何变化，得到的都是直角三角形。

师：你们仔细观察这些直角三角形，直角所对的弧刚好是半圆弧，另外两个锐角所对的弧加起来也刚好是半圆弧，因为这两个锐角的和也是90°。

学生仔细观察，都发现了这一现象。

师：你们太厉害了，这一知识要到中学才会学，你们现在就发现这一现象，已经很不错了。

接着教师又借助于投影呈现如图10圆外绿色的区域，要求在这一区域内任意找一点，再与A、B连结成三角形，并提出：这样连结成的三角形又是什么三角形？

图10

学生在练习纸上，按以上要求连结三角形，继续思考交流。

当学生发现这样连结的三角形都是锐角三角形时，教师又提出：请大家在圆内也任意找一点，连结的三角形又是什么三角形呢？

学生又经过操作、度量后，发现这样连结的三角形是钝角三角形。

此时学生的好奇心被激发。教师顺势在投影上出示：过一个钝角三角形顶点，画出底边上的垂线，此垂线交于圆弧上一点，这一点与A、B连结成的又是一个直角三角形。并向学生提出：通过刚才画图过程的观察，你能说出一些道理吗？

（评析：我们知道在“图形与几何”相关知识的教学中很重要的一点是如何尽量做到化静为动。一般在演示动态图形之前，应先让学生观察静态的图形去想象动态的变化，然后再利用媒体演示，使学生在观察中再次验证自己想象的过程。上文教师在教学中已较好地演绎了这样的想象过程。可以看到在第一步教学时，教师先让学生针对三个三角形进行观察、分析，并展开想象，然后把三角形的顶角沿着高所在的直线进行上下移动，使学生感受到随着顶角变化而引起的底角的变化。同时这一步的想象又为下一步的练习提供思路，在接下来的环节中教师巧妙地设计了“圆”与“三角形”的相关知识。另外，执教教师非常清楚这些知识是以后要学习的内容，此课上不要求学生去搞清这是为什么，只要求学生通过这样的过程，发现在圆弧上任意取一点C分别连结点A和点B，连结出的三角形都是直角三角形。显然这样的设计很好地激发了学生好奇心，使学生从中感受到数学的内涵和魅力。）

【总评】

回顾本课的练习，我们深刻地体会到，作为教师，全面、深入掌握学科知识是多么重要。我们都会说 “只有深入才会浅出”，但这仅仅是一个必要条件，还需要教师有着深入思考的意识与习惯。只有把知识点放到整体结构中去思考，才会想到如何去进行知识的渗透;只有教师有这样的思考意识，才能想到如何去进一步拓展学生思维。关于“三角形内角和是180度”这一知识，在小学阶段是用实验的方法（测量、剪拼）来获得，到了中学还需要进一步通过演绎推理的方法加以证明。到中学学习相似三角形知识时，最为重要的是认识三个内角对应相等、对应边成比例，然而在以上教学中，执教教师有意识地让学生根据一个直角三角形的三个内角度数画一画三角形，这样就自然地渗透了相似三角形的知识。而关于任意的凹多边形的内角和可以用“（n-2）×180°”来计算，就是在划分三角形时要根据图形特点注意有不同的方法，所以执教教师在练习时只给学生呈现两个特殊的凹多边形，并在教学时采取点到为止，仅给学生带来一些思考。同样在学习圆的知识时，圆周角的度数的知识是相当重要的，尤其直径所对的圆周角是直角，而四年级的学生通过作图会发现这样的事实，教师的目的是借助于这样事实，引发学生深入地思考。由此可见，只要教师能有意识地针对学习内容，适当创设拓展性的练习，同时注意把握好练习的度，学生一定会在练习中感受到数学是如此好玩。

（浙江省临海市临海小学   317000

浙江省临海市教育局教研室   317000）