TIMSS 2015数学评价框架（四年级）

曾小平 刘长红

国际数学与科学教育成就趋势研究（The Trends in International Mathematics and Science Study，简称TIMSS），是由国际教育成就评价协会（The International Association for the Evaluation of Educational Achievement，简称IEA）组织的大型国际教育评价研究项目。该研究的目的在于，评价各国中小学数学与科学教育成就的发展趋势，研究各国数学与科学教育成就同文化背景、教育制度等影响因素的关系，帮助各国提升数学和科学教育质量。

TIMSS自1995年起，每4年进行一次，第五次已于2011年完成[1];第六次将于2015年进行，主要针对四年级、八年级学生进行。下面我们对TIMSS 2015数学评价框架（TIMSS 2015  Mathematics Framework[2]）中四年级的数学内容作详细介绍，相信对数学教育评价会有所启发。

一、TIMSS数学评价概要

TIMSS认为数学教育对学生的发展极为重要，所有的孩子都能从学习与形成坚实的数学技能中获益。因为学习数学可以提高他们解决问题的技能，并培养他们的恒心与毅力。数学是日常生活中计算、理财和建筑等活动的工具，同时也是工程、建筑、会计、银行、商业、医药、生态和航空航天等诸多职业的基础。此外，在科技发达的信息社会中，数学对于经济与金融来说也是至关重要的。

TIMSS四年级数学评价框架尽量贴近各参与国家和地区的数学课程标准，尤其关注当前的数学教育研究与改革。比如，美国的“共同核心数学标准”（Common Core State Standards for Mathematics[3]）、新加坡的“数学教学大纲”（Mathematics Syllabi）和中国香港的“数学课程指引”（Mathematics Curriculum Guide）。

TIMSS重点评价基础知识的掌握和数学思考的过程。TIMSS 2015四年级数学重视数学问题解决的评价，有三分之二的问题考查学生的推理和运用技能。评价包括知识和认知两个领域，“知识领域”（Content Domains）侧重对代数与几何的评价，“认知领域”（Cognitive Domains）侧重对推理的评价。

二、数学评价的知识领域

TIMSS 2015四年级数学评价框架的“知识领域”包含“数”“几何形体与测量”和“数据呈现”三个区域，各区域所占比重分别为50%、35%和15%。其中，“数”和“数据呈现”分别相当于我国数学课程中的“数与运算”和“概率与统计”。

（一）数（Number）

TIMSS 2015认为整数及其运算是小学数学的基础，学生要能够使用合理的形式进行运算，并能借助运算解决问题。由于物体和数量并不总是整数，学生还要认识到，分数也是计算的基础，学生要比较熟悉分数与小数。此外，代数知识在小学已有渗透，学生需要理解简单方程中的未知量，还要初步理解变量之间的相互关系。

在四年级的“数”领域，TIMSS 2015重点评价“数与运算”中基础知识的理解与基本技能的掌握，该领域由“整数”“分数与小数”和“符号、方程和关系”三个部分构成，评价比重分别为25%、15%和10%。

1.整数

说明位置值，识别和书写数字的拓展形式，能使用文字、语言和符号表征整数;整数的大小比较;整数的四则运算;解决特定情境中涉及测量、货币和简单比例等内容的问题;辨认奇数与偶数、因数与倍数。

2.分数与小数

认识分数可以表示整体中的某些部分、集合中的某些部分或者数轴上的一个点，能使用语言、数字和模型来表征分数;分数的相等与大小比较，分数的加减运算（包括在具体问题情境中的加减运算）;用语言、数字和模型解释小数的位值制，小数的相等与大小比较，小数的加减运算（包括在具体问题情境中的加减运算）。（注：四年级的分数只限于分母是2、3、4、5、6、8、10、12的分数，小数只限于一位小数和两位小数。）

3.符号、方程和关系

发现算式中缺失的数字或者运算符号（比如，确定17+x=29中的x是多少）;使用算式和符号表征未知的问题情境;识别和使用已知模式中的数量关系（比如，根据数列的前几项写出后面一项，进而发现数列的规律）。

（二）几何形体与测量（Geometric Shapes and Measures）

TIMSS 2015认为，我们生活在不同形状与不同大小的物体构成的世界里，几何有助于我们发现和理解形状和大小的关系。学习几何重在培养空间观念，学生要能够按要求画出几何图形，能够在解决问题中分析和使用几何关系，学生要会使用工具和仪器来测量长度、角度、面积和体积，并利用公式计算长方形与正方形的周长和面积。

该领域包括“点、线和角”与“平面图形与立体图形”两个部分，仅涉及测量、坐标平面、线和角，还包含物体的体积与表面积。

1.点、线和角

测量与估计长度;识别和画出平行与垂直的直线;识别、比较和画出不同类型的角（比如，直角、锐角和钝角）;利用直角坐标系确定平面上的点。

2.平面图形与立体图形

描述和比较图形的基本属性（包括线和旋转对称性）;确定立体图形某个侧面的形状特征;计算多边形的周长和长、正方形的面积，利用密铺方法估算图形的面积，利用填充方法估计立体图形的体积。（注：四年级的平面图形涉及三角形、四边形和圆，立体图形涉及长方体、正方体、圆柱和圆锥。）

（三）数据呈现（Data Display）

TIMSS 2015认为，我们置身于信息社会的海量数据当中，互联网、报纸、杂志、教科书、参考资料和文章等以图表的形式向我们提供了大量数据。四年级学生要能够面对简单的情境和给出的数据，阅读和识别各种形式的数据。同时，四年级学生还要能够以图表的形式组织和表征数据，能够对比数据的特征，进而得出合理的结论。

该领域包含一个主题，即“阅读、解释和表征”。具体要求是：对统计表、象形统计图、条形统计图、折线统计图和扇形统计图中提供的数据进行阅读、解释和表征;挖掘数据中隐含的信息来解决问题（比如，在解决问题和执行计算中使用数据，组合数据，根据数据得出结论）。

三、数学评价的认知领域

TIMSS 2015四年级数学评价框架的“认知领域”包括“知道”“运用”和“推理”三个层次，各层次所占比重分别为40%、40%和20%。

（一）知道（Knowing）

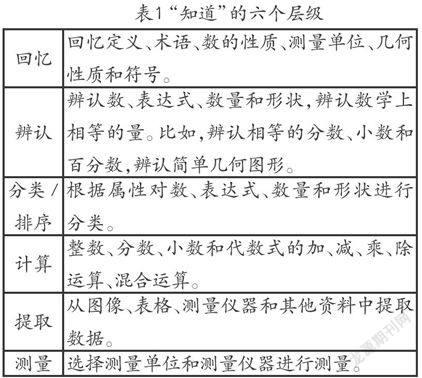
“知道”层次，涵盖了学生需要知道的数学事实、概念和程序。该层次包含“回忆”“辨认”“分类/排序”“计算”“提取”和“测量”六个层级，各层级含义见表1。

表1 “知道”的六个层级

回忆 回忆定义、术语、数的性质、测量单位、几何性质和符号。

辨认 辨认数、表达式、数量和形状，辨认数学上相等的量。比如，辨认相等的分数、小数和百分数，辨认简单几何图形。

分类/

排序 根据属性对数、表达式、数量和形状进行分类。

计算 整数、分数、小数和代数式的加、减、乘、除运算、混合运算。

提取 从图像、表格、测量仪器和其他资料中提取数据。

测量 选择测量单位和测量仪器进行测量。

数学应用的能力和数学情境的推理，依赖于熟悉的数学概念和熟练的数学技能。比如，学生能够回忆更多的相关知识，能够明白更广泛的概念，能够解决更大范围的问题。

如果缺少基础知识、符号表示和空间关系，那么学生很难进行有目的的数学思维。因为它们是基本的数学语言、基本的数学概念、基本的数学结论和数学思想的载体。

程序（算法，回忆和执行一定行动）架起基础知识与运用数学解决问题，尤其是那些人们在日常生活中遇到的问题之间的桥梁。学生需要高效和准确地使用多种计算程序和工具，来解决一般的典型问题，而不只是个别问题。

（二）运用（Applying）

“运用”层次，着重于评价学生运用知识和概念的理解来解决问题或回答问题的能力。该层次包含“确定”“表征/建模”和“实施”三个层级，各层级含义见表2。

表2 “运用”的三个层级

确定 使用通常方法，确定有效的/适当的操作、策略和工具来解决问题。

表征/

建模 利用表格或图表展示数据;在问题情境中建立等式和不等式、几何图形、图表建立模型，对数学图形和关系进行等价表征。

实施 利用熟悉的概念和程序，实施策略和行动来解决问题。

“运用”层次涉及数学在一定背景和范围内的应用，要求学生熟悉数学事实、概念、程序和问题解决。学生需要借助数学事实、技能和程序的知识与对数学概念的理解来进行数学表征，数学思想是进行数学思考和交流的核心，而创造等价表征的能力是在数学上取得成功的基础。

解决问题是“运用”的核心，重点是熟悉日常任务。问题可能来源于现实生活，也可能来源于数学内部，比如数或代数表达式、函数、方程、几何图形和统计数据等。

（三）推理（Reasoning）

“推理”层次，侧重评价学生对非常规问题的解决方案，比如不熟悉的情况、复杂的环境和多步骤的问题。该层次包括“分析”“整合/综合”“评价”“结论”“概括”和“论证”六个层级，各层级含义见表3。

表3 “推理”的六个层级

分析 在数、表达、数量和形状中确定、描述或使用关系之间的关系。

整合/

综合 联系不同知识单元、相关表征和程序来解决问题。

评价 评价解决问题的不同策略和方案。

结论 在信息和证据的基础上做出有效的结论。

概括 得到更一般的或者更广泛的结论。

论证 为方法和策略提供数学支持。

“推理”需要逻辑性和系统性思维，它包括：基于模式和规律的直觉与演绎推理;在新颖的或者陌生的情境下寻找解决现实问题或者纯粹数学问题的方案。这两种情况都需要转换知识与技能以面对新的情境，而推理是其中的共同特点。

“推理”中列举的很多认知技能都会在思考和解决新颖的或者陌生的问题中表现出来。这是数学教育价值的外在表现，然而更多的是对学习者思维的内在影响。比如，推理不仅需要观察和猜想能力，还需要基于特定假设、规则和正确结果的逻辑演绎推理能力。

四、四年级数学的评价样题

在TIMSS 2015数学评价框架的“附录”中，给出了一些评价样题。通过这些样题，我们可以更好地了解TIMSS 2015四年级数学评价的形式、理念与重点。

1.如图1所示，某人以固定的速度从A地骑车去B地，2小时后她来到一个路牌前。此人以同样的速度骑车，再有多长时间可以到达B地？（）

图1

A. 小时       B.2小时       C.3小时       D.3小时

2.某人有12个苹果，她吃了一些，还剩下9个。下面哪个算式更能够表达这件事情？（）

A.12+9=□          B.9=12+□

C.12-□=9        D.9-□=12

3.甲吃了块蛋糕，乙吃了块蛋糕，他们一共吃了多少蛋糕？

答案_______。

4.下面选项中，哪一个折叠之后，能成为右边的盒子？（   ）

5.如图2所示，某人在墙角堆了一些盒子，每个盒子的大小都是一样的。他一共用了多少个盒子？ （   ）

图2

A.25       B.19       C.18       D.13

6.某人调查了她的朋友们最喜欢的颜色，得到了以下信息（见表4）。然后，她画出图来表示这些信息，请帮助她把图画完。

表4 最喜欢的颜色统计图表

颜色 最喜爱

的人数

红 4

绿 2

蓝 6

黄 7

（参考答案1.C;2.C; 3.¾块; 4.D ;5. C;6.略 。）

通过这些样题，我们可以体会到TIMSS 2015四年级数学评价的侧重点是：重视对学生问题解决过程的评价，重视评价学生数学推理和数学运用的能力，重视评价学生基础知识的掌握和数学思考的过程。

【参考文献】

[1]曾小平等. TIMSS2011数学评价：“框架”“结果”与“启示”[J]. 数学教育学报，2013，22（6）：79-84.

[2] TIMSS 2015 Mathematics Framework [EB/OL]. http：//timssandpirls.bc.edu/timss2015/frameworks.html.

[3] 曾小平，刘效丽. 美国“共同核心数学课程标准”的背景、内容、特色与启示[J]. 课程·教材·教法，2011，31（7）：92-96.

（首都师范大学初等教育学院   100048）