建构联系 厘清脉络 提炼方法

朱国平 崔琴

【教学内容】六年级下册总复习“平面图形的认识”。

【教学目标】

1.通过整理和复习使学生进一步掌握平面图形的特征，能依据图形的特征沟通各图形之间的联系。

2.引导学生将分散的知识进行系统整理、归纳和沟通，促进知识的系统化和结构化，并从中领悟整理知识的方法。

3. 体会分类、集合等数学思想。

【教学过程】

一、点明课题，引发回忆

师：上节课我们复习了有关线和角的知识，今天我们继续整理和复习有关平面图形的知识。（板书课题：“平面图形的认识”整理与复习）

二、分类梳理，构建联系

（一）引导整理三角形

1.从“角”的角度整理

（1）出示：

师：如果在这个锐角上再添一条线段围成一个三角形，想一想，可以围出哪些不同类型的三角形？ 在作业纸上画一画。

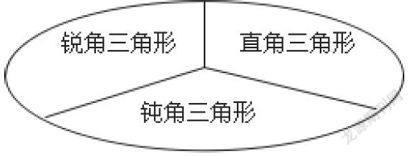
生：锐角三角形、直角三角形、钝角三角形。（课件演示，黑板贴出三类三角形）

（2）出示：

师：如果在直角和钝角上也添一条线段能围出什么三角形呢？在头脑中画一画。

师：为什么直角和钝角只能画一种三角形，而锐角能画三种呢？

师生小结：应用了三角形内角的特点，由于内角和是180度，一个三角形至少有两个锐角，最大角的类型决定了三角形的类型。（板书：内角和180度，至少2个锐角）

（3）三角形分类

师：三角形按角的特征分类，有这样三类，我们可以用这样的关系图表示它们的关系（板书如下图）：

（设计说明：复习课教学材料的选择至关重要，优质的教学材料能迅速勾起学生对旧知的记忆。本环节从“在角上再画一条边，能画哪些类型的三角形？”开始，引出按角分类的三类三角形，通过对不同角画出三角形类型的辨析，学生自觉应用了三角形角的特点。学生的思维也在这 “回忆—应用—整理”的过程中被调动起来。）

2.从“边”的角度整理

师：刚才我们从“角”这个角度整理和复习了三角形，那如果从边的角度去分析，该怎么去研究呢？

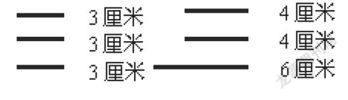
出示：

师：哪三根小棒可以围成三角形，并想象一下它的形状，想好后和同桌交流一下。

生1：可以围成等边三角形，用三根3厘米的小棒。（黑板贴出：等边三角形）

生2：还可以围成等腰三角形。（黑板贴出：等腰三角形）

师：用哪几根小棒围成等腰三角形？

生3：（4，4，3）、（3，3，4）和（4，4，6）。

生4：还有（3，3，6）。

生5：这个不行，因为3+3等于6。因为三角形的任意两边之和要大于第三边。（板书：a+b>c）

生6：拼出锐角三角形，用（3，3，4）。

师：你能确定吗？

生6：我觉得可能性很大，但不能肯定。（课件演示结果）

师：根据三角形的三条边的确可以判断它的类型，但这要等到初中再学习。

师：刚才有同学能根据边的长度估计出它的类型，请你想象一下（4，4，6）和（4，4，3），这两个三角形的形状有什么不同？

生7：（4，4，6）的形状有点矮，可能是钝角三角形。

生8：（4，4，3）的形状有点高，可能是锐角三角形。

（课件出示结果）

师：刚才拼的三角形都是特殊的三角形，有没有围出一般三角形的？

生：（3，4，6）可以围出一个普通三角形。（生说明理由）

师：能否围成三角形的依据是什么？

生：任意两边之和大于第三边。（板书：三边关系）

师：三边的长度确定了，形状和大小就完全确定了（课件演示），所以三角形具有稳定性，谁来举个生活中的例子？（板书：稳定性）

3.整合三角形的关系

师：如果把等腰三角形、等边三角形也放进这个关系图里，应该放在什么位置？

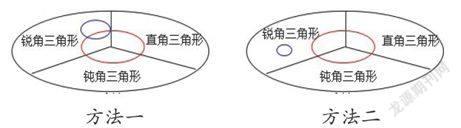
学生出现两种方法，如下图

方法一                                 方法二

（注：大圈表示等腰三角形，两个小圈表示等边三角形）

师：这两种画法的相同点是什么？

生1：都找到了锐角三角形和等边三角形之间的关系。（学生都同意）

师：这两种画法的不同点呢？

生2：因为有些等边三角形是等腰的，有些不是，我觉得方法一是对的。

生3：不对吧！等边三角形一定是一个等腰三角形。我觉得两个方法都不对。

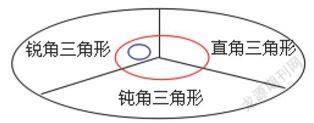
生4：应该把等边三角形放在等腰三角形中属于锐角三角形的部分，因为等边三角形既是等腰三角形又肯定是锐角三角形。（黑板画出圈）

师：这样画既能看出等边三角形和锐角三角形的关系，又能看出它和等腰三角形的关系。看来找到正确的位置挺不容易的，考虑问题一定要全面。

4.整理方法回顾

师：刚才从哪些方面整理和复习三角形的？

师：从三角形的角、边入手，复习了它们的特征，理清了它们的关系。这也是复习平面图形的一种方法。我们能不能用这样的复习方式来整理整理四边形？

（设计说明：本环节学生再次经历从“边”的角度“回忆—应用—整理”三角形，能促使学生形成复习“图形与几何”知识的基本方法，即从图形的特征入手厘清图形之间的关系。一般情况下，两种分类方法是相互独立的，本环节却进行了沟通，尤其在“等边三角形该放什么位置？”引发学生的思考，在辨析中逐步明确应从整体上思考图形之间的关系。）

（二）自主整理四边形

1.自主整理，出示要求。

师：我们学过的四边形有哪些？想一想它们的特征？画一画它们的关系图。

2.有选择进行评价。

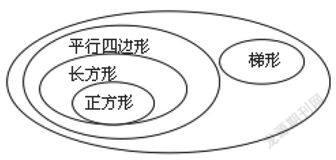
3.再次修改关系图，形成如下板书：

4.根据关系图，回答：

（1）梯形和平行四边形最大的区别是什么？ （板书：平行）

（2）为什么说正方形和长方形是特殊的平行四边形？（板书：垂直）

（3）正方形为什么是特殊的长方形呢？

5.小结。

师：平行四边形有两组对边互相平行，梯形只有一组，它们都属于特殊的四边形。

（设计说明：本环节从“边”和“角”的角度整理四边形，在学生自主整理的过程中应用整理平面图形的基本方法，在辨析中明确四边形之间的关系。）

（三）简单整理圆

师：在小学里，我们除了学习这些三角形和四边形，还学习了哪个图形？

生：圆。（板书：圆）

出示问题链，回答：

1.圆和这些图形最大的区别是什么？（曲线图形）

2.圆能分类吗？（不能，形状是一样的）

3.圆有什么特征？（半径、直径及相互关系，圆周率，对称性等）

（板书：半径—大小    圆心—位置）

师：三角形由三条边围成，边的特点决定了三角形的类型，四边形也是如此，但圆的大小是一条半径决定的，形状也是唯一的。

三、回顾小结，提升认识

师：这节课咱们对这些平面图形进行了整理，我们是怎么复习的？

师：两个完全一样的等腰直角三角形可以组成什么图形？4个呢？（出示下图）

观察这些图形，有什么相同点和不同点？

师：图形之间可以互相转化，可以通过这些联系去推导图形的面积计算方法。

【本课总体构想】

复习课的教学任务主要有三：一是对学生的知识掌握情况进行查漏补缺，帮助学生整理所学知识，理清知识的来龙去脉，构建知识体系;二是提高学生应用知识解决问题的能力;三是复习方法指导，培养学生自主学习、自主复习的能力。而要完成这些任务需要教师对复习课的教学进行有效的设计。

一、复习的目标需有层次性

复习课不仅要求在教师的引导下帮助学生理顺认知脉络，更深层次的要求就是注重学生能力的提高，提升学生的思维品质。本课中可以提炼出两条主线：一条“主线”是知识层面，沟通知识点之间的联系并串联成线;另一条“主线”是方法层面，让学生领悟复习的方法，提升思维品质，促进学生复习能力的形成。

二、复习的材料需找准切入点

本课复习的知识点分布范围广，学习跨度大，如何在有限的课堂时间中达到有效复习的目的？我们认为找准复习材料的切入点尤为重要。在本次课中，我们选择从三角形的“角”和“边”两个维度进行整理和复习，并按角分类和等腰三角形、等边三角形进行了沟通，在自主整理四边形的过程中则让学生举一反三、触类旁通。以边和角作为图形复习课的切入点，让整节课的线索清晰、层次递进，用“点”的知识为牵引，实现了“面”知识的梳理，从而提升了复习的有效性。

三、复习的方法需提炼和应用

“授人以鱼不如授人以渔”。本课在复习的方法上遵循“回忆—应用—整理”的教学模式。在课中，教师提供给学生开放性的教学材料充分交流，给学生足够的时间梳理知识，引导学生提炼和归纳整理知识的方法并加以应用。学生在课堂上不仅收获的是知识，其复习能力也得以提升。

（浙江省湖州市湖师附小教育集团   313000）