华北地区强震的等待时间研究

2015-09-04孙丽娜齐玉妍金学申

中国地震 2015年2期

孙丽娜齐玉妍金学申

河北省地震局，石家庄市槐中路262号 050021

0 引言

强震的孕育、发生是极其复杂的物理过程，离上次发生强震的时间越长，离下一次地震的时间不一定也越长。Garavaglia等(2007)的工作指出，如果考虑强震的发生只取决于从上一强震之后的若干时间发生，那么在某区域的地震预测是可能的。

假设某地区在某时间发生了一次强震，对于如何判断下一次地震的发生时间，许多研究者从不同的角度对不同环节提出了各种有益的探索。然而，就地震复发模型而言至今仍主要沿用泊松过程的假定。当去除余震后，小地震活动符合泊松分布(Gardner et al，1974)，而在一个较大范围里的中强地震活动在时间轴上却遵从成丛分布(Knopoff et al，1996)。按照这个假设，周期性的地震活动遵从有限的成丛性，可以精确地预测。一般来说，如果有时间上的聚集性，且在已有地震时间分布的前提下，那么就可以计算未来一定时间间隔的发震概率。为了定量描述这一性质，我们把在给定区域自上一次强震以来的持续时间与在给定时间间隔范围内的强震发生的条件概率联系起来，计算强震在给定时间的发生概率。

本文从概率论的原理出发，推导出计算强震等待时间的公式，然后依据各分布模型，得到等待时间的计算公式，在此基础上，计算了河北省及邻近地区的5.0级以上强震等待时间的概率。

1 下一次地震的等待时间

假定P(t)是地震时间间隔的概率密度，而t是自上一次地震以来的时间，t'是从现在到下一次地震发生的时间间隔，即等待时间(Sornette et al，1997)。现在的问题是要求得t'的概率密度函数P(t')。据贝叶斯条件概率公式

我们假定P(A)=P(t+t')，这就是从现在开始到下一次地震发生时的时间间隔为t'的概率。同时假定也就是从上一次地震发生到现在没有地震发生的概率。这样，归一化的条件概率公式为

建筑施工总包商和分包商的实际经济、技术实力仍存在着较大差异，针对这一情况，建筑施工单位各部门应对此建立合理有效的施工技术管理体系，对于传统的建筑施工技术管理体系进行转型，建立和健全施工技术管理体系，形成专业部门从而管理施工技术工作，保证在分包时，建筑施工单位要落实管理责任工作，将责任落实到各个部门。另外，施工企业在工程施工过程中，应做好各部门的协调工作，调整工作人员调动，发挥工作人员的自身优势，做到人尽其才，加强各部门在施工过程中的配合工作，使各部门相互协助完成工作，进而在保证工程质量的前提下提高施工效率。同时，施工企业单位要重视施工人员业务素质能力，定期对施工人员进行职业素质培训。

由(2)式得平均等待时间为

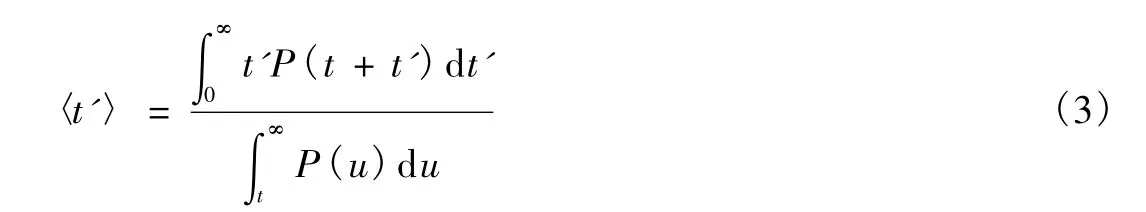
通过简单的变量变换u=t+t'，可以得到

由分部积分，得到

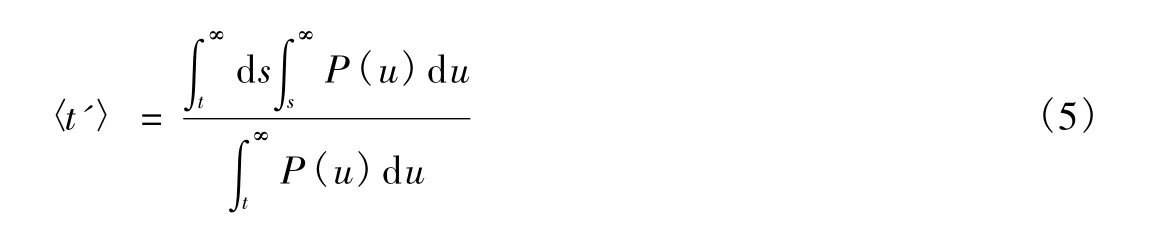
为简单起见，把(5)式写成

f(t)是p(u)的二重积分，因此有

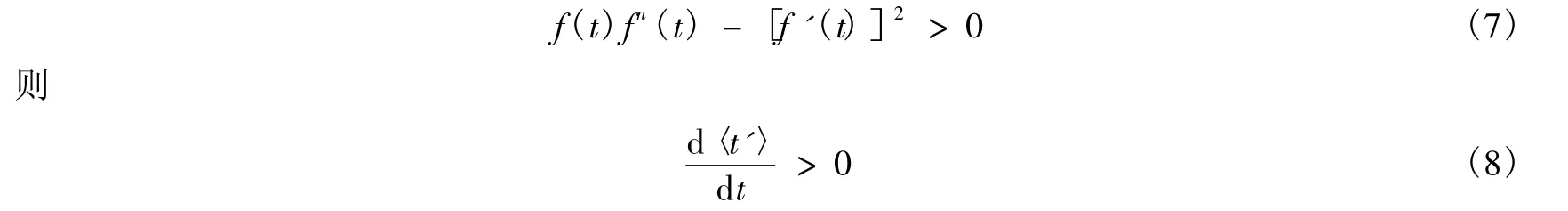
同样，设f(t)=e－g(t)，如果g″(t)＜0，则如果P(t)在t=0时有限，我们也能发现(5)式的变换形式，这对等待时间短的情况十分有用。因为对短的等待时间，有积分结果可以直接据(5)式得到:〈t〉是两地震间的平均重复时间，设其中τ是等待时间的估计值，它是根据上一次地震以来的时间估计得到的。我们把它看作为t'的瞬时估计。这样就可以写成

如果瞬时估计τ小于平均的等待时间，那么，到下一次地震的时间随着离逝时间的增加而增加，这表明平均等待时间反应的是整个时间中各部分的贡献。而如果〈t〉的值大于τ，则表明这是在非零时刻大于τ的那部分的贡献。在这种情况下，如果〈t〉小于τ，离下一次地震的时间随着离逝时间的增加而减少。在特殊情况下，如果P(0)=0，则离下一次地震的时间随着离逝时间的增加而减少。如果P(0)=∞，则即离下一次地震的时间随着离逝时间的增加而增加。

2 各种分布的概率密度函数

假设上次地震起至现在的时间为t，其概率密度函数为p(t)，现在起至下次发生地震的间隔时间为t'的概率密度函数为P(t');现在起至下次发生地震间隔时间在u以内的概率为Pr(u)。则由(2)式可得

根据这些分布函数的定义，结合(2)式和(11)式用分布函数来计算下一次强震的等待时间概率。

2.1 指数分布

我们首先考虑指数分布，因为它与泊松分布相似，指数分布的等待时间的表达式为

其中t0是平均间隔时间。由(2)式，可得

很显然，下一次地震的发生时间不取决于离逝时间，不管t的值有多大，从现在到下一次地震的平均时间都为t0。则

2.2 均匀分布

均匀分布的表达式是

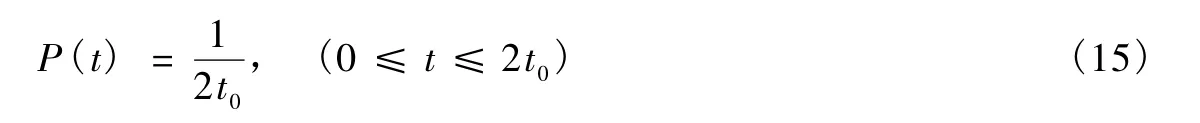
其中2t0是地震间最大的时间间隔，t0是其平均值。由(2)式，有

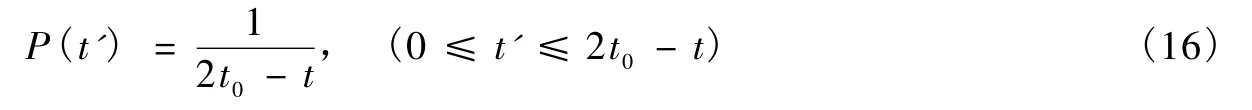
P(t')与t'无关，也就是说，它本身是一个均匀分布，但其值取决于t，在未来一直到t0的时间内，发生一次地震的概率随着离逝时间的增加而增加，而当离逝时间超过2t0时，等待时间就变得不确定了。这实际上也就告诉我们，下一次地震的发生时间在2t0内的可能性最大，而这从公式也可以看出。如果是负的，这表明等待时间随着离逝时间的减少而减少。则

2.3 威布尔分布

威布尔分布的表达式为

3 t0的确定

在上述计算中，我们不知道t0，所以要据有限的地震时间间隔来估计。假定我们有(n-1)个地震时间间隔，并忽略其不确定性(而这对历史地震来说是可能的)。假定最后一次地震的离逝时间为t，那么，在泊松分布的情况下，由最大似然法给出的t0的估值是

t为最后一次地震距今的时间间隔，tj为n个地震间的时间间隔。

这样，在泊松分布的情况下，得到了随离逝时间的增加而增加的下一次地震复发的平均时间间隔。(21)式可以被推广用于上述其他分布(Sornette et al，1997)。

4 强震的等待时间预测方法在河北及周边地区的应用及回溯性检验

根据黄玮琼(1994)对我国大陆地震资料的完整性研究成果，按华北地区(除海域与边远地区外)的记载能力，对公元1303～1500年有记载的6级以上的地震和公元1500年后有记载的5级以上的地震，用统计分析方法进行检验，得出华北地区(除黄海及边远地区外)M地震自1484年之后基本完整。因此，本文将公元1500年以来的地震目录(去除余震)用于等待时间的数学模型计算。

本文将预测研究区划分成:河北南部、晋冀蒙、京津、唐山4个区域(表1)，用公元1500～1970年的5级以上的地震目录计算了这4个地区从1970～2070年这100年内各时段发生5级及以上地震的概率(图1)。

表1 研究区域的划分

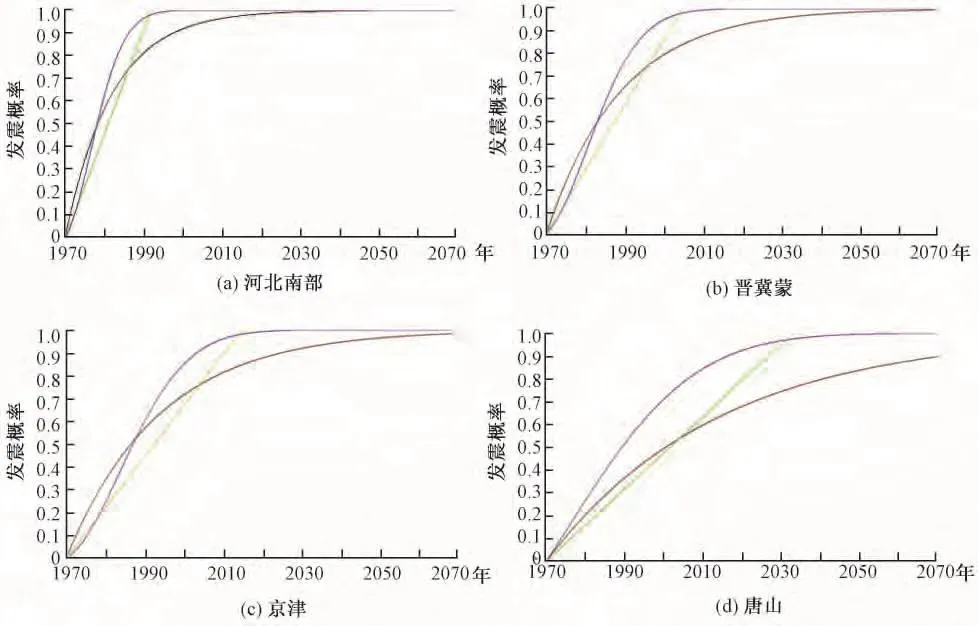
图1 研究区域5级以上地震在1970～2070年的发震概率

本文设发震概率为P，当P≥0.6时，认为将会发生5级及以上的地震，则P=0.6是发生地震的最低阀值，因此对P=0.6、0.7、0.8这3个分布计算的发生5级及以上地震的概率值所对应的时间，进行回溯性检验。结果如表2～5所示。

据表2～5可以看出，河北南部和晋冀蒙地区检验率比较高，计算出来的发震时间和实际发震时间比较接近甚至一致。京津地区和唐山地区检验率略低一些，分析京津和唐山地区的计算过程发现，这两个地区在1500～1970年间5级及以上地震的时间间隔比较大，这可能是造成检验率低的关键因素。

表2 河北南部地区回溯性检验结果的对比

表3 晋冀蒙地区回溯性检验的对比结果

表4 京津地区回溯性检验结果的对比

表5 唐山地区回溯性检验结果的对比

5 AIC判别准则

统计模型的优劣可以用(Akaike，1997)提出的一种AIC准则来判别，此准则实质上是一种最大熵估计。其方法是:假定lnL是所得到的模型的对数最大似然值，则

其中，L为统计分析中的最大似然数，K为参量数目。对于不同模型计算出的AIC值，AIC值最小的模型作为最优来选择。两个模型的AIC值相差越大，模型的优劣差别就越明显，反之差别不大(朱守彪等，2002)。一般来说，AIC值相差2以上时，这两个模型就可以比较其优劣(孙若昧等，1999)。

表6 研究区三个分布函数模型的AIC值

本文用AIC准则对研究区的3个分布函数模型进行判别，计算结果如表6。比较表6的AIC值，发现在这4个研究区内，3个分布函数模型中均是指数分布模型的AIC值最小，且这3个分布函数模型的AIC值都相差2以上，AIC准则适用于判断这3个分布函数模型的优劣。结合回溯性检验的结果，本文认为指数分布模型比较适合于这4个研究区域内强震等待时间的计算。从图1的(a)、(b)、(c)、(d)均可以看出在2013年以后的发震概率比较高，这为地震的中长期预测提供了参考。