基于BP神经网络预测普梳纯棉纱断裂强力

杨　陈

(江西服装学院， 江西 南昌 330201)

基于BP神经网络预测普梳纯棉纱断裂强力

杨陈

(江西服装学院， 江西 南昌 330201)

通过构建BP神经网络模型，寻求棉纤维断裂比强力、细度、长度、表面摩擦系数、纱线捻度、毛羽量及条干均匀度与普梳纯棉纱断裂强力之间的关系。

BP神经网络；棉纱；断裂强力；影响因素

纱线的断裂强力即纱线在受力条件下保持纱线力学特性的一个重要性能指标，它不仅能够影响纱线在织造过程中上机工艺的设计，还能够影响织物的力学性能、耐磨、起毛起球等多项织物服用性能指标[1]。影响纱线断裂强力的因素众多，对普梳纯棉纱而言，影响棉纱断裂强力的因素主要由棉纤维本身的强度、棉纤维的细度、棉纤维的长度、棉纤维表面摩擦系数、纱线的捻度、棉纱的毛羽数量及条干均匀度等7个主要因素，可以说棉纱的断裂强力是由一个多自变量因素构成的目标函数。本文通过BP神经网络构建棉纱断裂强度与多自变量影响因素的BP神经网络模型以预测棉纱与多自变量影响因素之间的函数关系，进而对普梳纯棉纱的断裂强力在纺制前能够定量地精确分析，为生产实践提供一定的参考依据。

1　BP神经网络工作原理

Back Propagation(BP)神经网络是由McCelland和Rumelhart提出的一种无须事前分析计算目标函数与多自变量因素中的每个因素之间的函数关系，而是从网络层面通过网络函数关系误差逆传播算法训练的多层前馈映射建立起来的网络函数关系。BP神经网络的使用可以在构建目标函数与多因素自变量函数反向传播误差运算时，不断调整目标函数与多因素自变量函数网络的阀值与权值，而使得函数模型的误差平方和最小，从而获得较高的相关性[2～3]。BP神经网络的模型的结构主要包含函数关系的输入层、隐层与输出层，其主要的工作原理是通过大量自变量信息协同处理的一个非线性函数关系系统。目标函数的输出层每经过一次训练后，即把所得期望值与实际输出的差距通过BP神经网络反向传播，进而对自变量函数进行调整，通过中间隐层函数可以不断调整目标函数模拟的阀值与权值进而不断提高目标函数与实际测试值之间的相关性。

2　实验部分

2.1实验材料及仪器

实验材料为棉纤维与由该棉纤维纺制出来的18.2 tex的普梳棉纱，仪器为Y162A型束纤维强力机、Y151型纤维摩擦系数测定仪、LL881Y-4型电热恒温鼓风干燥箱、HFB-408S可程式恒温恒湿试验箱、Y331A型电子纱线捻度仪、Y162A型束纤维强力机、PTT-A+200千分之一电子天平、YG171D型纱线毛羽测试仪、YG133型条干均匀度仪。

2.2实验方法

2.2.1棉纤维影响因素指标测试

将棉纤维在温度105℃的LL881Y-4型电热恒温鼓风干燥箱中烘至恒重后，将其放置到温度为20℃，相对湿度为65%的HFB-408S可程式恒温恒湿试验箱中平衡24 h，以下实验测定数据的棉纤维均是使用经标准大气压平衡后的棉纤维。

(1)棉纤维断裂强力测试

利用Y162A型束纤维强力机夹持棉样为8 mm，棉束宽带为4 mm，断裂强力精确为9.8 cN，下降速度为300 mm/min条件下测试棉纤维的断裂强力，实验次数为45组。

(2)棉纤维细度测试

利用PTT-A+200千分之一电子天平称取平衡后的棉纤维称取8～10 mg，棉纤维根数在1500～2000根，利用中段称重法测试棉纤维的平均细度，实验次数为45组。

(3)棉纤维长度测试

利用PTT-A+200千分之一电子天平称取平衡后的棉纤维50 mg，采取罗拉法棉纤维长度测试的方法测试棉纤维的长度，实验次数为45组。

(4)棉纤维表面摩擦系数测试

参照实验说明书，制作棉纤维辊，使用Y151型纤维摩擦系数测定仪测定棉纤维与棉纤维辊之间的纤维表面摩擦系数，测定过程中张力夹选择100 mg，棉纤维动态表面摩擦系数测定过程中，纤维辊的转速为30 rpm，静态表面摩擦系数测定过程中，保持棉纤维转速为0，记录棉纤维与棉纤维辊瞬间滑移时的扭力天平计数，棉纤维的动态与静态表面摩擦系数均测试45组。

2.2.2棉纱影响因素指标测试

将普梳纯棉纱在温度105℃的LL881Y-4型电热恒温鼓风干燥箱中烘至恒重后，将其放置到温度为20℃，相对湿度为65%的HFB-408S可程式恒温恒湿试验箱中平衡24 h。分别采用加捻退捻法使用Y331A型电子纱线捻度仪测试棉纱的捻度，使用YG171D型纱线毛羽测试仪测试毛羽指数，使用YG133型条干均匀度仪测试棉纱的条干均匀度。

2.3实验数据的处理

棉纤维断裂比强度(cN/dtex)、棉纤维细度(dtex)、棉纤维长度(mm)、棉纤维表面摩擦系数、纱线捻度(捻/10cm)、棉纱毛羽数量及条干均匀度(%)等7个影响因素的数据指标参数如表1所示。

表1　影响普梳纯棉纱断裂强力因素指标参数

本次实验棉纱数据组数共45组，其中9组数据为测试数据，另外36组数据为BP神经网络训练数据。BP神经网络模型构建前，首先对所收集实验数据均按照最大值为1，最小值为0设置，将目标变化与各自变量实验数据按照公式1进行归一化处理，使之均在[0,1]的区间范围内[4]。本次研究所构建的神经网络模型为3层BP神经网络模型，BP神经网络模型中的目标函数即为棉纱断裂强力，而自变量因素为上述所收集的7个棉纱强力影响因素指标(BP神经网络隐层神经元数目的多少是根据公式2确定的，隐层神经元过多会引起学习时间过长而导致目标函数与多因素自变量之间过度拟合的情况发生，而隐层神经元数目过少又会导致BP神经网络模型精度的下降，因此，依据公式2确定隐层神经元数目为4～13个较为合适)。

(1)

其中，xi—目标函数及各自变量归一后数据，数据分布的区间为[0,1]；x—未经归一化处理的目标函数及各自变量；xmin—未经归一化处理的目标函数及各自变量数据中的最小值；xmax—未经归一化处理的目标函数及各自变量数据中的最大值

(2)

其中，n1—BP神经网络模型中隐层神经元数；n—BP神经网络模型中输入层神经元数；m—BP神经网络模型中输出层神经元数；a—1～10之间的常数。

2.4BP神经网络模型构建编程

实验数据归一处理完成后，调用MATLAB中按照下列参数对BP神经网络模型进行构建，在神经网络模型中设置BP神经网络的层数为3层，其中输出层所用传递函数为logsig(s型的对数函数)，隐层传递函数为tansig(s型正切函数)，训练方法采用traing-cg算法，均方误差采用mse函数算法。神经网络模型的算法采用标准的BP算法。数据训练次数上限为50000次，数据预测精度为0.005。

3　实验结果与BP神经网络模型分析

3.1BP神经网络模型隐层神经元个数确定

以棉纤维的强度、棉纤维的细度、棉纤维的长度、棉纤维表面摩擦系数、纱线的捻度、棉纱的毛羽数量及条干均匀度等7个影响因素的数据为BP神经网络模型的输入参数，以棉纱断裂强力H为BP神经网络的输出层参数，BP神经网络中隐层的神经元个数的取值范围在4～13区间变化，分别构建10个BP神经棉纱断裂强力BP神经网络模型。使用归一处理后36组数据对所构建的BP神经网络模型进行训练，训练后统计不同隐层神经元个数时BP神经网络的模型误差。测试结果如图1所示。从图1可以明显看出，当BP神经网络模型中隐层神经元个数的数目为10个时，BP神经网络输出层的均方误差为0.02916，为该BP神经网络误差的最小值。因此，确定为BP神经网络隐层神经元个数为9个，构建BP神经网络模型结构为7-9-1。

3.2BP神经网络模型隐预测结果与实验数据相关性

BP神经网络预测棉线断裂强力预测值与棉纱断裂强力实验值结果如表2所示。使用公式3对BP神经网络模型隐预测结果与实验数据相关性进行计算可知，BP神经网络模型隐预测结果与实验数据相关性系数为0.91132。由此可知，在训练次数为50000次，数据预测精度为0.005的条件下，BP神经网络模型对棉纱断裂强力具有很强的预测性。

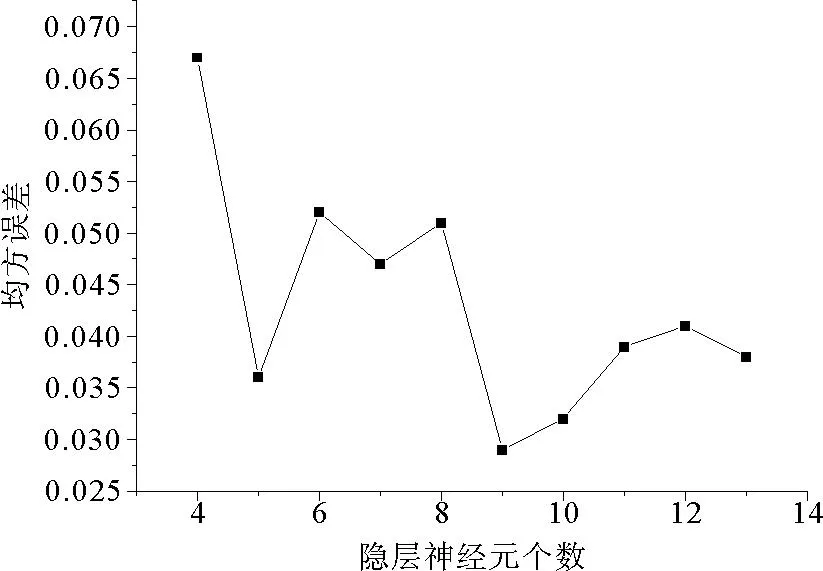
图1　BP神经网络隐层神经元个数与均方误差关系曲线

(3)

其中，r-BP神经网络模型隐预测结果与实验数据相关系数；x-BP神经网络预测棉线断裂强力值/cN；y-棉纱断裂强力实验值/cN；n-实验组数。

表2　BP神经网络预测棉线断裂强力预测值与棉纱断裂强力实验值结果

4　结论

通过BP神经网络构建棉纱断裂强力与棉纤维的强度、棉纤维的细度、棉纤维的长度、棉纤维表面摩擦系数、纱线的捻度、棉纱的毛羽数量及条干均匀度等7个影响因素网络模型表明当BP神经网络模型中隐层神经元个数为9个时，预测值与实验值之间的误差最小为0.02916，相关系数为0.91132，具有较强的预测性。

[1]毛萃萃，张弦，王廷荣.捻系数和毛羽值与棉纱强力的相关性分析[J].现代纺织技术，2012,32(1):1—3.

[2]张黎明，张秉森.改进LMNP神经网络在织物染色配色中的应用[J].青岛大学学报(工程技术版)，2010,25(1): 15—17.

[3]史步海，朱学峰.LMBP神经网络改进算法的研究[J].控制工程，2008,15(2):164—167.

[4]Babay A, Cheikhrouhou M, Vermeulen B, et al.Selecting the optimal neural network architecture for predicting cotton yarn hairiness[J].Journal of the Textile Institute, 2005,96(3):185—192.

Predict Breaking Strength of Pure Cotton Carded Yarn by BP Neural Network

YangChen

(Jiangxi Institute of Fashion Technology, Nanchang 330201, China)

The model of BP neural network was set up to explore the the relation of breaking strength of pure cotton corded yarn with the factors of cotton fiber breaking strength,fineness,length,surface friction coefficient,yarn twist,hairiness and irregnlarity.

BP neural network;cotton yarn;breaking strength;influential factors

2015-07-19

杨陈(1980—)，男，重庆人，讲师。

TS101.9

A

1009-3028(2015)06-0025-04