热泵供暖系统动态操作节能优化

丁强，邢长新，江爱朋，程文，周大寒

(杭州电子科技大学能量利用系统与控制研究所，浙江 杭州 310018)

引 言

随着人们生活水平的提高，建筑供暖的需求越来越大，对于以空气源热泵产生热量驱动的供暖系统而言，在保持一定的舒适性前提下进一步降低系统能耗费用具有重要意义。为了实现热泵系统的节能和优化运行，研究者分别从多个方面对热泵系统进行分析和改进。林澜等[1]利用热经济学优化方法对热泵供暖系统进行了较全面的热经济学分析；清华大学江亿院士[2]对建筑能耗系统进行了综合分析，提出了节能策略。早在20世纪70年代，Stoecker[3]就开发热泵机组的稳态仿真通用程序，建模时在符合稳态仿真规范的前提下对各部件的工作过程作了高度简化，该模型可以完成系统性能的预测。Hiller[4]建立了可变容量空气源热泵系统的稳态数学模型,用以计算不同稳态运行工况下的系统性能。美国能源部橡树岭国家实验室(ORNL/IxE)对热泵和制冷系统进行了深入的研究，特别是建立了一套从MARKI 到MARKV 系列的空气源热泵的稳态模型以及完整的系统数值仿真系统，并在工程中广泛应用[5]。基于能源动力的考虑，部分研究者采用太阳能、废热等作为热泵的驱动动力，以此节省电力消耗。张颖等[6]对基于太阳能驱动的热泵供暖系统进行了综合分析，给出了直膨式和非直膨式两种太阳能热泵供暖系统的流程，并分析了参数变化对其的影响。清华大学史琳等[7]近年来对热泵空调系统仿真和控制方面的研究状况做了全面分析，指出了存在的研究难点和今后的研究方向。除了对热泵系统性能改进提高其性能系数等方面研究外[8-9]，采用系统工程技术对系统的优化操作和控制来提高热泵系统的性能是目前研究的一个重要着力点，该方法早已被证明是行之有效的提高生产效益和质量的方法，已应用于多种工业生产流程[10-12]。对于其中涉及的优化求解方法，也随着计算机技术和数值优化技术的进步而逐步完善[13-15]。

对于热泵供暖或者与建筑结合的人工环境系统，一些研究者根据系统运行特点进行了分析。例如考虑到一天内电价和环境温度的不同，Rink 等[16]研究了不同时均电价情况下的热泵系统优化控制问题，采用极大值原理方法获得热泵系统运行过程的最优操作模式。Nassif 等[17]提出了一种简化的基于模型的优化控制方法，通过采集监控数据和建立的VAV 系统模型可以在线获得控制器的设定值，从而实现优化控制目标。Logist 等[18-19]将热泵系统性能情况与建筑供暖集成起来考虑，根据集成系统的动态模型对其多目标优化控制进行研究，获得不同目标要求下的Parato 解。

本文在以上研究的基础上，考虑环境温度变化和电价变化情况，采用联立求解的方法将动态优化命题转化为非线性规划问题进行求解，并根据优化仿真结果给出满足一定舒适度下的最低能耗优化方法，以期进一步降低系统能耗费用。

1 系统模型

空气源热泵供暖的基本原理如图1所示。热泵系统通过压缩做工的方式吸收空气中的能量，从而使得热泵工质的温度升高，热泵工质通过传热将热量传递给热泵中的进水，使得热泵中的进水温度由Twr上升到Tws。如不考虑循环损失，由能量守恒则可以得到热泵出水温度变化方程，如式(1)所示[18]。

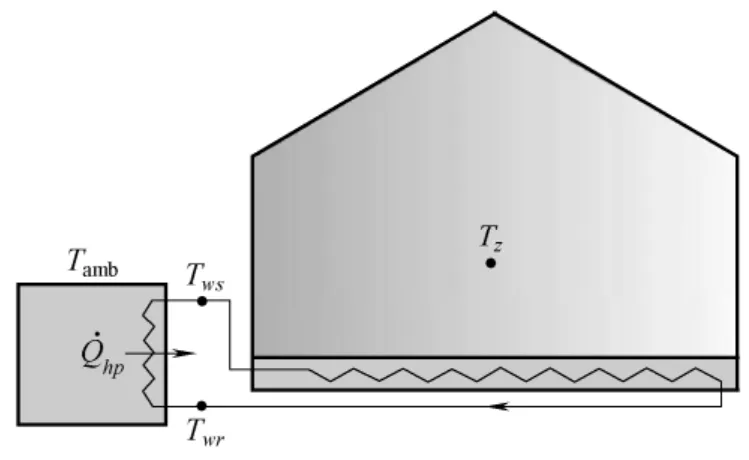
图1 热泵供暖示意图Fig.1 Schematic diagram of heat pump heating system

式中，表示热泵的输出功率。加热后的热泵出水被输送到建筑中用于供暖，在此过程中循环水回水温度降低到Twr,，这部分热量通过热传导加热室内温度，使得室内地板表面温度Tf升高。回水温度的变化情况可近似为式(2)所示。

而地板表面温度的变化则可表示为如下形式

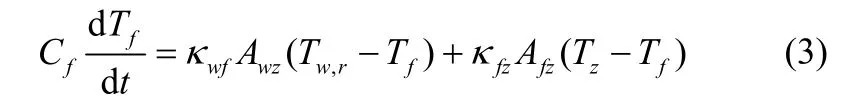
因为供暖系统释放的热量并没有完全用于对地板的加热，因此地板的吸热量和供暖系统放热量不相等。被供暖的建筑内室温Tz变化主要由两部分决定，一部分是地板表面温度上升对室温的加热作用；一部分是外界环境变化使得散热量发生变化。室温的动态变化可表示为以下形式

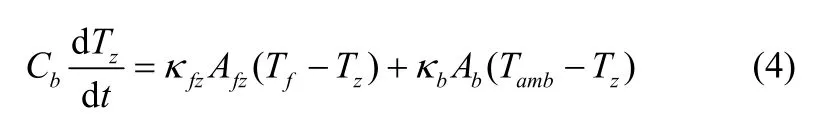
对于热泵系统而言，其加热热水所输出的功率与其输入功率（热泵压缩机功率）和热泵的性能系数相关，可表达为如下形式

式中，Php表示热泵压缩机功率，COP(t)表示热泵性能系数，其值与热泵的输出热水温度、外界环境温度相关，而环境温度随着时间变化而变化。性能系数可表示为以下形式

式中，α1、α2、α3、α4、α5均表示与系统结构相关的系数，可通过热泵生产厂家或者实际数据拟合得到。热泵供暖系统通过控制运行频率来控制热泵压缩机的功率（热泵输入功率），进而控制热泵供水温度Tws。在环境温度变化的情况下，由于建筑散热损失也发生变化。因此热泵供暖系统在相对稳态情况下，提供的热量与散热损失相当。散热损失Qb,ss可表示为

这里 1β＞表示实际热损失与向房间散热的比值。对于热泵系统，其运行过程热量释放量与运行频率、温度等关系通过实验数据拟合可得

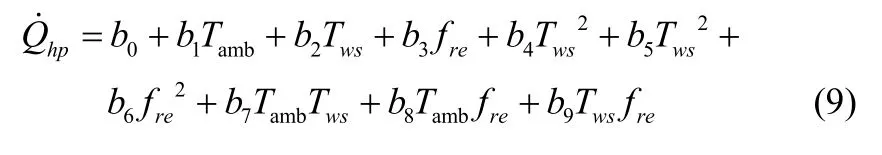
2 优化问题及求解

基于空气源热泵和建筑结合的供暖系统在功能上主要是实现建筑内温度的舒适性，正常情况下设计目标温度一般在15～25℃，热泵系统通过控制热泵压缩机功率来控制进入建筑物的热水的温度，假设室内目标设定温度为Tz,ref，而实际室内平均温度为Tz(t)，那么常规控制的目标就是使得室内实际温度尽量跟踪设定温度，使得控制误差尽可能小，这时控制目标可表示为

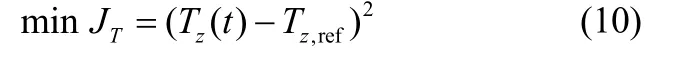
考虑到系统运行过程中操作费用问题，也希望在满足一定设定温度控制容限下尽可能地降低能耗费用，实现系统的优化节能控制。系统的操作费用主要体现在空气源热泵系统的能耗费用，其值与用电量和不同时刻的用电价格有关。其能耗费用目标表示为

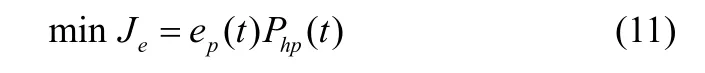
由于热泵的运行功率、能效比和建筑散热消耗等都与环境工况(如环境温度)有很大关联，而环境工况随着天气的变化而变化，这就使得系统的运行费用和对设定温度跟踪目标随着环境工况的变化而动态变化。在一定的时间区域[0tend]内，既考虑系统能耗又考虑室内温度控制精度的综合目标可表示为

式中，ep(t)表示不同时刻的用电价格，K表示平衡两个目标的权重情况。在K=1 时，优化目标表示为单一的温度控制目标；在K=0 时，优化目标为单纯的电费最低为目标。为了实现系统优化控制，可根据对设定温度跟踪容忍度的要求选择合适的K值，从而既满足用户对温度舒适度的要求，又使得系统能耗降低。因此系统模型中应加入如下 条件

对于热泵供热系统，环境温度虽然在一天内变化较大，但在相邻的天数内具有一定的准周期性。为研究方便，优化目标函数式(12)以24 h 作为一个优化周期，并使得在优化终止状态和优化开始状态相同。这里定义其反映了系统供暖的主要温度变化情况，那么在优化开始和终止时刻系统状态可表示为

并且满足如下边界约束

将以式(12)为目标、以式(1)～式(9)和式(13)～式(15)等为约束的优化控制命题命名为Opt1。由于该命题模型方程中既含有非线性代数约束，又含有4 个微分方程，因此该优化命题为非凸的非线性动态优化问题，加上系统中含有一定的不等式约束，导致其求解具有一定的难度。传统的极大值原理和控制变量参数化方法在求解该问题时无论求解精度还是求解效率上都有较大难度[14]。为求解以上形式的DAOPs 问题，采用联立方法将微分方程通过配置等多项式近似，从而将原问题转化为非线性规划（NLP）问题，然后采用基于内点、稀疏等技术的优化可以快速精确地得到优化解，有利于本操作优化问题。该方法通过配置在有限元上的一组多项式来近似微分方程中的状态变量和控制变量。该多项式一般为拉格朗日插值多项式或者正交多阶多项式。这里采用单项式基表示的有限元配置方法，该方法具有龙格-库塔离散过程的多种优势

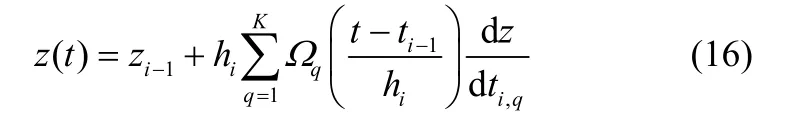
式中，1iz-表示在第i个有限元初始处的值，hi是第i个有限元的长度，dz/dti,q表示其在第i个有限元上，配置点q处的一阶导数。Ωq为满足以下条件的KK阶多项式

微分方程的连续性方程为

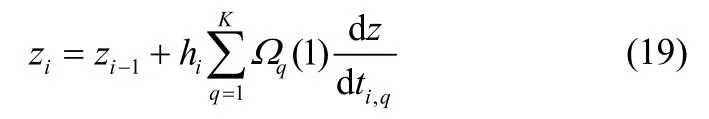
根据Biegler 团队的一些研究[14-15,20]，Radau 配置点对高阶DAE 方程的具有更好的稳定性，这里采用了Radau 配置点。对于控制变量和代数变量采用拉格朗日基形式的插值多项式表示。形式如下

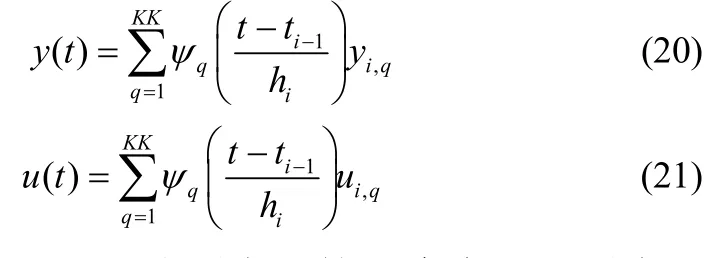
式中，yi,q和ui,q分别表示第i个有限元置点q处的代数变量和控制变量值，且满足ti-1≤t≤ti，ψq为KK阶拉格朗日多项式。

通过以上离散配置方法，微分代数方程描述的优化命题转化为非线性规划问题。为了保证一定 的精确度，离散化后的问题变量规模虽然相对较 大，但可采用内点和稀疏等技术对其进行快速优化求解。

3 实例分析

为分析以上优化控制的节能和温度控制情况，这里以浙江某地的空气源热泵供暖情况进行分析。图2为浙江某地冬季24 h 环境温度变化的典型情况，图3表示空气源热泵供暖系统的性能拟合情况。图4给出了该地一天内的用电价格时均变化情况。这里房间设定温度为20℃。供暖系统中的相关参数值则如表1所示。

采用联立优化求解技术对所建立的优化命题进行求解，首先将0～24 h 划分为48 个控制单元，使得系统每0.5 h 调整一次热泵输入功率(压缩机功率)；在每个控制单元内配置10 个有限元，每个有限元内选择3 个配置点。然后在GAMS 平台下采用 IPOPT 求解器对离散化后的NLP 问题进行优化求解，从而得到满足相应要求的最优操作和系统内部状态变化情况。

图2 浙江冬季24 h 温度典型曲线Fig.2 Typical daily ambient temperature of Zhejiang in winter

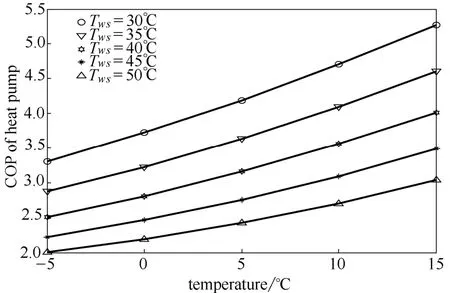
图3 热泵性能拟合曲线Fig.3 Fitted curves of air source heat pump COP

图4 一天之内的电力价格变化情况（EP-1）Fig.4 Time-of-use(TOU) electricity price（EP-1）

表1 动态方程中的参数值Table 1 Parameter values of model

3.1 不同权重K 下的优化结果

由优化目标函数式(12)可以看出，本文的优化目标前一部分反映的是系统的运行能耗成本，后一部分是系统对控制目标(舒适性)的考虑。这里将优化目标函数中后一项的开方定义为不舒适度。当K=1 时，只考虑舒适性，也就是使房间内温度Tz尽可能接近目标温度。因此，选择不同的权重值K，就势必会对运行成本和舒适度产生影响。为了使目标函数中两个目标的值大小均衡，对于优化目标函数进行标度化处理，处理后的目标函数如下

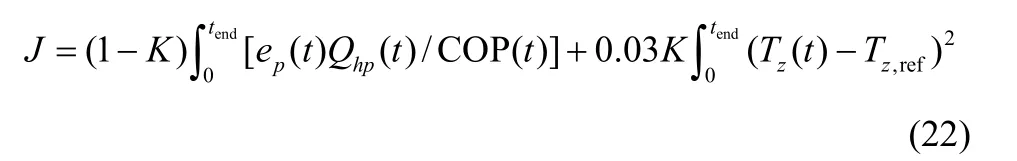
对优化目标函数采用不同权重，同时暂时不规定实际室温对设定温度的跟踪误差容限，在此情况下对系统进行优化求解，得到不同情况下系统运行成本、室内不舒适度、室内温度、热泵输出功率的情况，如图5～图8所示。

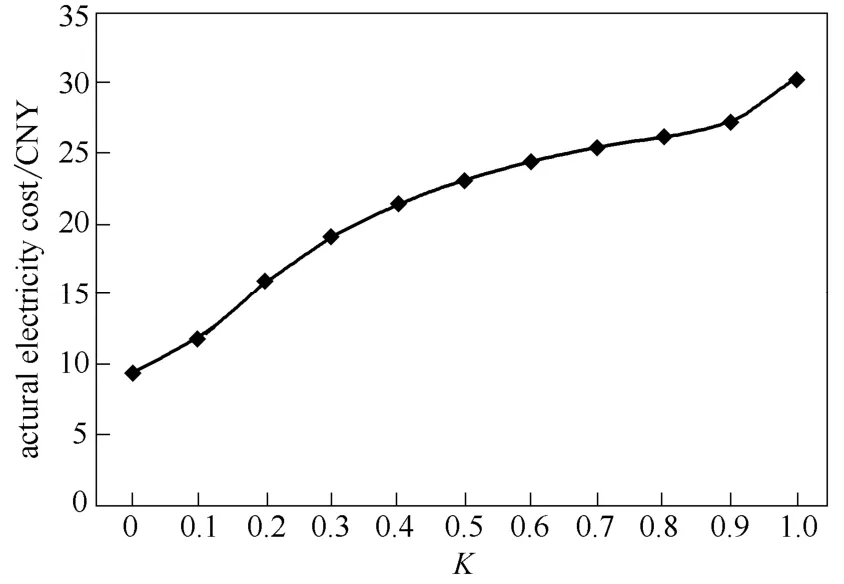
图5 不同权重值K 下的电力消耗情况Fig.5 Electricity cost with different weights

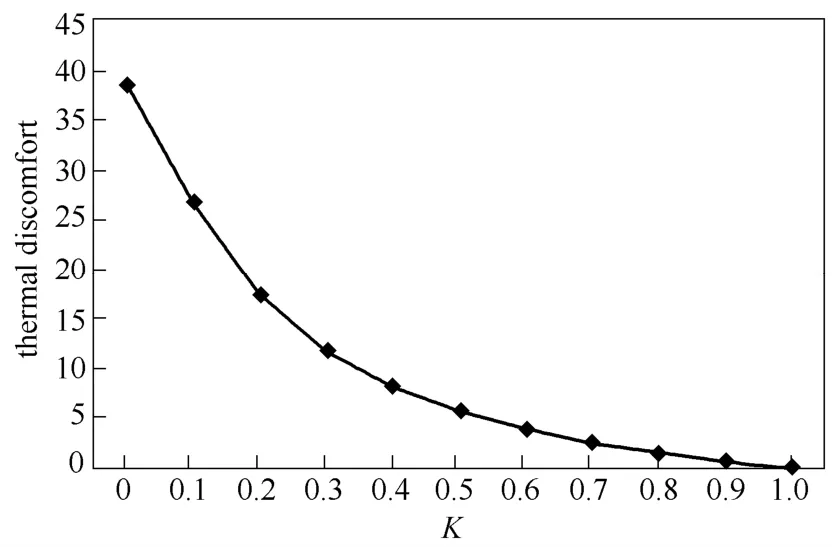
图6 不同权重值K 下的不舒适度情况Fig.6 Profile of thermal discomfort with different weights

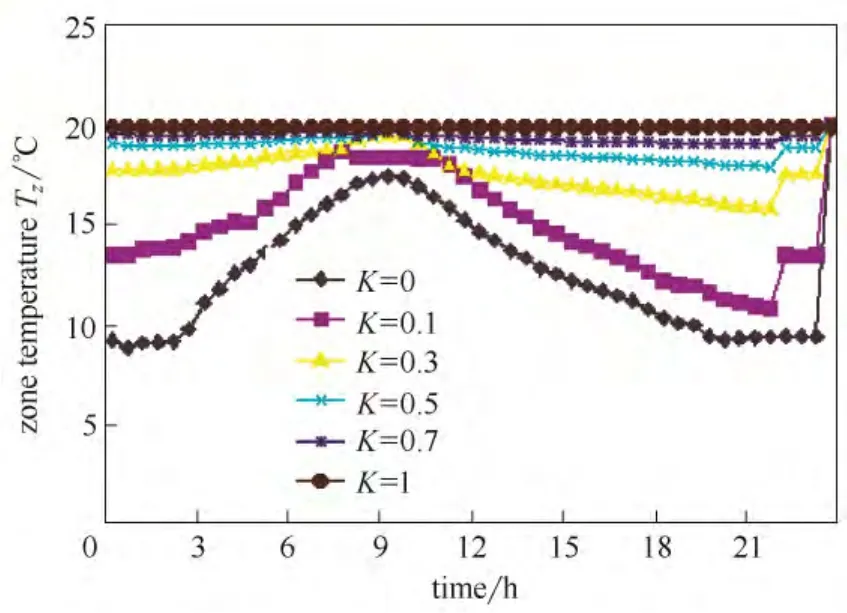
图7 不同权重值K 下的室内温度情况Fig.7 Profiles of indoor temperature with different weights

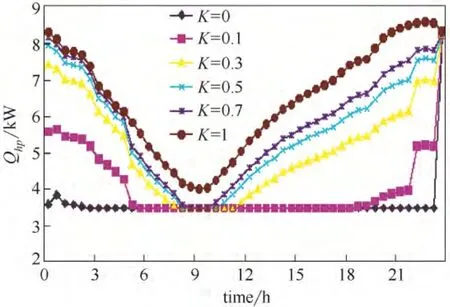
图8 不同权重值K 下的热泵输出功率曲线Fig.8 Optimal thermal power curves with different weights

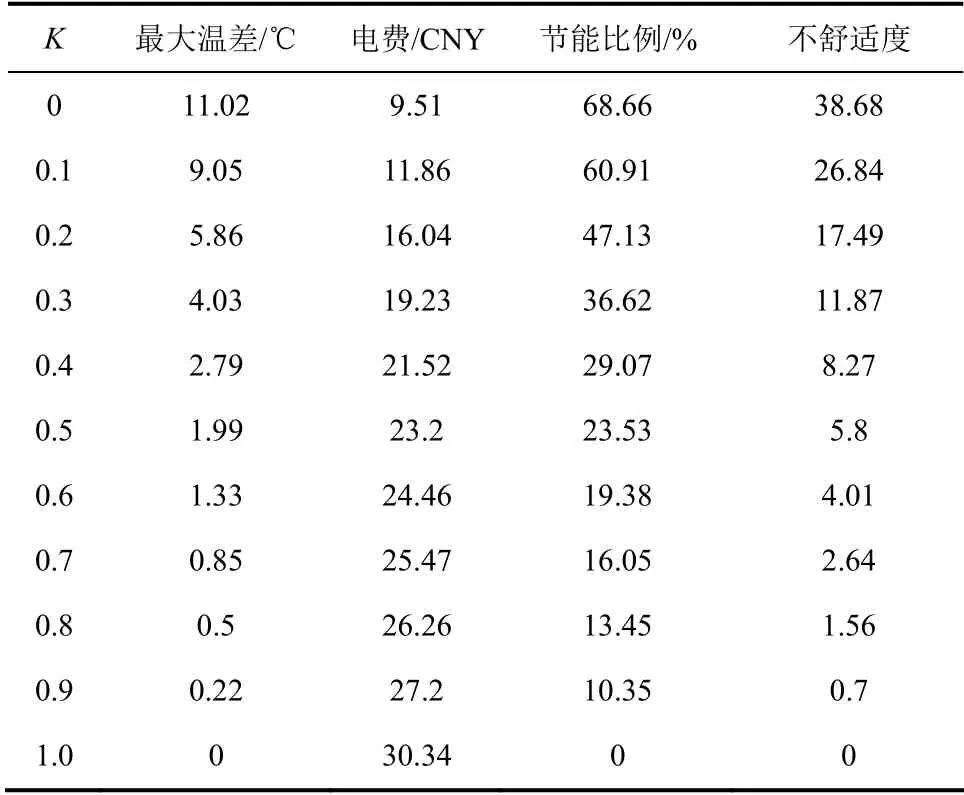
表2 不同权重下的最大温差、电费和节能情况Table 2 Results of max temperature difference and energy cost

由图5可以看出，在不同的权重值K值下，房间供热一天的用电费用也大幅度改变，在K=0 的 时候，用电费用仅为10 CNY，当然这是以舒适度的牺牲为代价的。而当K=1 的时候，用电费用需要30 CNY 以上。可以看出，在权重值由1 变到0的过程中，系统的不舒适度明显升高。表2给出了系统在不同K值下的房间内温度与目标温度的最大差值、不舒适度、电费和节能情况。在K=0 的时候房间内温度与目标温度的最大差值达到11.02℃，不舒适度达到了1552。这样的温差是用户所不能接受的。当K在0.3～1 范围内变化时，系统具有很好的节能效果，虽然存在一定的不舒适度（图7）。当K=0.7 时，不舒适度仅为7，房间内温度与目标温度的最大温差仅为0.85℃，而房间每天的用电费用却由K=1 时的30.34 CNY 降到了25.47 CNY，日用电费用节省超过16%，如果把K值设置在0.5，此时最大温差约为2℃，日用电费用节省超过23.53%。

图8表示不同K值下的系统输出功率情况。在环境温度较低时，热泵的输出功率较高；随着环境温度的上升，热泵的输出功率降低，供水温度也随之降低。这是因为在环境温度低的时候需要输出更多的热量，这时候热泵耗电功率也较高所致。对比不同权重值K下的供水回水地板温度曲线可以发现，在温度升高时较大K值的温度曲线与较小K值的温度曲线呈相反趋势，K值越大，热泵输出功率随温度升高而降低的幅度越大。通过以上问题的优化求解，还可以获得在目标值最优情况下系统在不同时刻的状态变化曲线，图9则给出了在不同权重K值下相对应的温度状态变化情况。

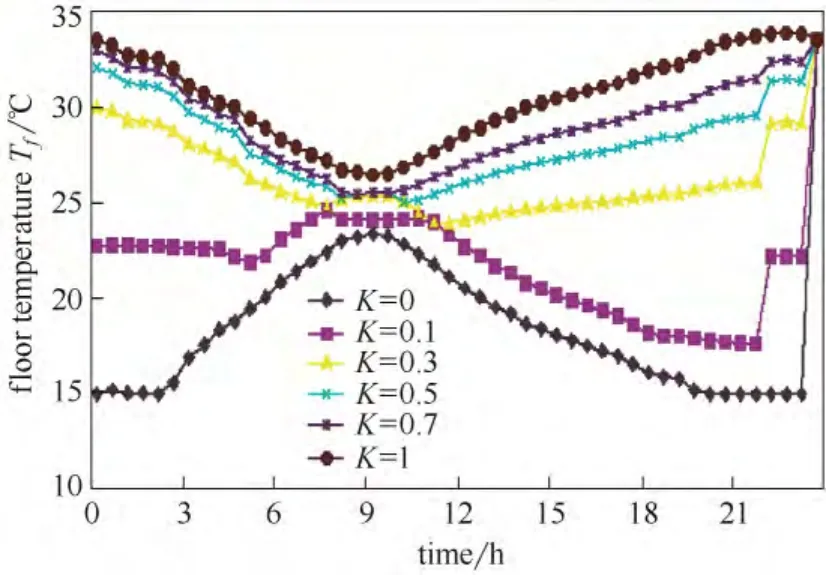
图9 不同权重K 值对应的回水温度情况Fig.9 Supply water temperature curves with different weights

3.2 基于权重动态调整的优化分析

由热泵性能方程可以看出环境温度对优化目标有重要影响，反映到能耗方面就是在环境温度高的时候系统能效比高，更有经济性。而电价在不同的时刻不同，也导致在不同时刻满足优化目标的成本不同。为了既能实现房间温度控制误差相对较小(在合理的容限内)，又能使得系统又具有更好的节能潜力，一种合理的选择是在电价相对较低、热泵性能系数较高的时候更加注重房间温度的控制精度，即更好地满足房间温度舒适性要求，而在相反的情况下更加注重降低系统能耗成本。根据以上原则，本文对式(22)所描述的优化目标进行调整，使得反映能耗成本和舒适性的两个指标的总体权重动态的变化，每0.5 h 调整一次，以期获得更好的优化效果。调整后的目标函数如下

其中，ep(t)表示不同时刻的电价，COP(t)的加入是为了在目标函数中体现环境温度对系统的影响。根据表2计算的结果分析，权重K的0.3～0.7范围时室内温度跟踪误差比较小，且节能效果也比较好。因此在这里选择K=0.7，并设定室内温度与目标温度的最大差值小于2℃，对以式(23)为目标的优化命题进行重新优化求解，求解时电价以图10中的电价分布为基础，由此得到相应的优化结果，并与式(22)为目标函数的优化结果进行比较。计算结果表明，采用本调整后的目标函数形式可以进一步获得更好的节能效果。调整后的用电费用为34.85 CNY·d-1，不舒适度为5.77，仍然满足设定要求；调整前的用电费用为36.56 CNY，不舒适度为4.262。总的系统能耗又进一步节省了近4.7%，这表明本文对优化目标策略的调整还是有明显效 果的。

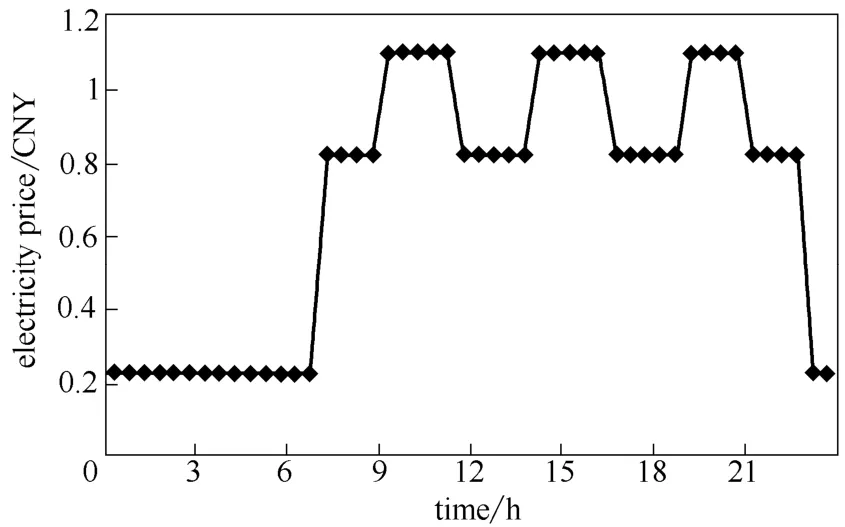
图10 时均电价情况2（EP-2)Fig.10 Profile of TOU electricity price (EP-2)

图11给出了策略调整前后的热泵输入功率操作变化情况和相关的状态变化情况。其中case A 表示以式(22)为目标函数的求解结果，case B 表示以动态调整权重的式(23)为目标的求解结果。从图中看出，优化目标变换后热泵输入功率的操作曲线在第12 h 以后变化相对明显，而不同策略下的室内实际温度变化曲线则反映了房间舒适度的变化情况，均处于设定的容差范围以内。

图11 目标函数调整前后的优化求解结果Fig.11 Comparison of optimal results before and after adjustment of objective function

4 结 论

本文在建立根据热泵供暖系统基本动态过程方程和整体优化目标的基础上，考虑了室温跟踪效果和能耗消耗的平衡，对热泵供暖系统的动态优化操作进行了分析和研究，提出了动态优化调整策略。结果表明：（1）在允许室温跟踪误差最大为0.85 的情况下，可以实现16%以上的能耗节省。在更高的舒适度容忍度内节能效果更大。（2）环境温度和电价是影响系统运行能耗的重要因素，根据这两个影响因素的变化提出的动态调整目标函数权重策略可以进一步降低系统能耗4.7%左右。

本文的研究结果对优化热泵供暖系统操作、节约运行成本具有一定的意义。在本文的基础上，拟开展考虑用户负荷和中间蓄热条件下的热泵系统优化操作和优化控制技术研究。

符 号 说 明

Ab——建筑与外部环境的换热面积，m2

Afz——地板与室内空气传热面积，m2

Awz——热水管道和地板传热面积，m2

b0,…,b9——结构系数

Cwr——回水温度为Twr的回水总热容，J·℃-1

Cws——Tws时系统总热容，J·℃-1

cw——水的比热容，J·kg-1·℃-1

COP(t)——热泵性能系数

ep(t)——不同时刻用电价格，CNY·(kW·h)-1

epmin——整个时段的最低电价，CNY·(kW·h)-1

fre——热泵运行频率,Hz

K——权重

——循环水量，m·s-1

Php——热泵压缩功率，kW

Qb,ss——散热损失，J

——热泵的输出功率，kW

Tamb——室外环境温度，℃

Tf——地板温度，℃

Twr——热泵进水温度，℃

Tws——热泵出水温度，℃

——参考供热温度，℃

Tz——室内温度，℃

Tz,ref——室内设定温度，℃

u(t)——控制变量

y(t)——代数变量

α1,…,α5——结构系数

β——比值系数

κb——建筑与外部环境的传热系数，J·m-2·℃-1

κfz——地板与室内空气传热系数，J·m-2·℃-1

κwf——供暖系统对地板的传热系数，J·m-2·℃-1

ψq——拉格朗日多项式

Ωq——有限元配置阶多项式

[1]Lin Lan (林澜),Hu Sangao (胡三高).Economic Optimization of heat pump heating system [J].Journal of North China Ⅰnstitute of Electric Power(华北电力大学学报),1988,(4):28-35.

[2]Jiang Yi (江亿).Chinese building energy consumption situation and energy efficiency strategy [J].New Architecture(新建筑),2008,(2):4-7.

[3]Stoecker W F.A generalized program for steady-state system simulation [J].ASHRAE Trans.,1971,77 (1):140-148.

[4]Hiller C C,Glicksman L R.Improving Heat Pump PerformanceviaCompressor Capacity Control:Analysis and Test [R].Cambridge:MIT Energy Lab,1976.

[5]Domanski P A,Didion D A.Mathematical model of air to air heat pumps:equipped with a capillary tube [J].Ⅰnternational Journal of Refrigeration,1984,7 (4):249 -255.

[6]Zhang Ying (张颖),Li Xiangli (李祥立),Duanmu Lin (端木琳),Peng Jun (彭俊).Research overview on performance of solar heat pump heating system [J].Gas & Heat(煤气与热力),2009,29 (8):24-29.

[7]Shi Lin (史琳),Xue Zhifang (薛志方).Simulation and control researches for heat pump /air conditioning systems:a review [J].HV&AC(暖通空调),2007,37 (8):50-62.

[8]Wu Jingyi (吴静怡),Wang Ruzhu (王如竹),Xu Yuxiong (许煜雄).Cycle characteristics and dynamic performance of continuous heat recovery adsorption air conditioning system/heat pump [J].Journal of Chemical Ⅰndustry and Engineering(China) (化工学报),2002,53 (2):144-149.

[9]Guo Junjie (郭俊杰),Wu Jingyi (吴静怡),Wang Ruzhu (王如竹),Zhang Jie (张洁) Xu Yuxiong (许煜雄).Experimental and thermodynamic analysis on the performance of an air-source heat pump water heater [J].Journal of Chemical Ⅰndustry and Engineering(China) (化工学报),2006,57 (12):120-124.

[10]Jiang Aipeng (江爱朋),Shao Zhijiang (邵之江),Chen Xi (陈曦),Fang Xueyi (方学毅),Geng Dazhao (耿大钊),Qian Jixin (钱积新),Zheng Xiaoqing (郑小青).Simulation and optimization of distillation column sequence in large-scale ethylene production [J].Journal of Chemical Ⅰndustry and Engineering(China) (化工学报),2006,57 (9):2128-2134.

[11]Jiang Aipeng (江爱朋),Shao Zhijiang (邵之江),Chen Xi (陈曦),Fang Xueyi (方学毅),Geng Dazhao (耿大钊),Qin Jixin (钱积新),Zheng Xiaoqing (郑小青).Operation optimization of distillation column based on reduced SQP algorithm and hybrid derivative method [J].Journal of Chemical Ⅰndustry and Engineering(China) (化工学报),2006,57 (6):1378-1384.

[12]Kim Y,Kim S,Kim Y,Lee S,Kim I,Kim J.Overview of systems engineering approaches for a large-scale seawater desalination plant with a reverse osmosis network [J].Desalination,2009,238 (1/2/3):312-332.

[13]Betts J T.Practical Methods for Optimal Control Using Nonlinear Programming [M].Philadelphia,Pennsylvania:SIAM Press,2001.

[14]Biegler L T,Cervantes A,Waechter A.Advances in simultaneous strategies for dynamic process optimization [J].Chemical Engineering Science,2002,57:575-593.

[15]Biegler L T.Nonlinear Programming:Concepts,Algorithms and Applications to Chemical Processes [M].Pittsburgh:Society for Industrial and Applied Mathematics (Cambridge University Press),2010.

[16]Rink R E,Gourishankar V,Zaheeruddin M.Optimal control of heat-pump/heat-storage systems with time-of-day energy price incentive [J].Journal of Optimization Theory and Applications,1988,58 (1):93-108.

[17]Nassif N,Kajl S,Sabourin R.Simplified model-based optimal control of VAV air-conditioning system//Ninth International IBPSA Conference [C].Montreal,Canada,2005:823-830.

[18]Verhelst C,Logist F,van Impe J,Helsen L.Study of the optimal control problem formulation for modulating air-to-water heat pumps connected to a residential floor heating system [J].Energy and Buildings,2012,45:43-53.

[19]Logist F,Houska B,Diehl M,Impe J V.Fast Pareto set generation for nonlinear optimal control problems with multiple objectives [J].Structural and Multidisciplinary Optimization,2010,42 (4):591-603.

[20]Biegler L T.An overview of simultaneous strategies for dynamic optimization [J].Chemical Engineering and Processing,2007,46:1043-1053.