气液两相分离的免方程多尺度模拟方法

杨晨，何航行

（重庆大学动力工程学院低品位能源利用技术及系统教育部重点实验室，重庆400044）

引 言

在现实问题中，流体或多或少总会含有其他物质，绝大多数流动属于多相流。气液两相流动现象广泛存在于能源、动力、石油、航天等多个技术领域，如核反应堆内的流动沸腾现象等。过去几十年中，各国学者对于一些典型的两相流动传热过程进行了大量的数值模拟研究。传统的数值方法很难模拟相界面动力学行为，无法刻画出两相流动的细 节[1-3]。同时，随着研究的深入，仅着眼于宏观尺度的模拟研究已经无法满足研究和发展的需求[4]。目前，基于微细尺度（微观尺度、介观尺度等）的模拟方法如动力学Monte Carlo 方法（KMC）、分子动力学方法（MD）和格子Boltzmann 方法（LBM）等是深入研究这些复杂过程的有效手段。直接运用这些方法在微细尺度上能够建立反映过程内在机理的微观模型和介观模型，但其模拟过程需要完全依赖计算量巨大的微细仿真器（fine scale simulator，FSS），经常面临计算机内存开销巨大、超出当前 计算能力的问题，以致无法实现对某些复杂实际 问题的模拟，导致微细尺度模拟研究面临极大的 困难[5]。

近年来，有学者提出了一种计算机辅助分析复杂系统的新型多尺度模拟框架——免方程方法(equation-free method，EFM)[6-7]。其关键思路是绕过从微细尺度模型中获得宏观模型方程这一传统过程，为复杂系统多尺度模拟提供了一种新的思路。目前免方程方法的研究在国外发展迅速，但国内只有少数文献提及。早在20世纪末，Theodoropoulos等[6]已涉及到粗粒化时间步进（coarse time-stepper，CTS）这种跨尺度耦合思想；2001年Gear 等[7-9]开始从事粗粒化投影积分（coarse projective integration，CPI）的研究；之后Kevrekidis 和Gear 等[10-13]运用免方程方法进行了一系列研究。由此，该多尺度模拟框架逐渐受到复杂系统模拟研究者的广泛关注，其应用研究也逐渐增多。

LBM 方法由于具有微观粒子特性，可以方便地描述不同相之间的相互作用，清晰地捕捉气液相界面[14]。因此，本研究充分运用这一优势，提出了一种用于模拟气液两相分离过程的免方程多尺度方法。利用该方法模拟水在van der Waals（vdW）、Redlich-Kwong（R-K）和Peng-Robinson（P-R）状态方程控制下的相变过程，发现多尺度模拟能够从微细底层很好地模拟出气液两相分离过程中密度的分布，所得结果与LBM 单尺度模拟十分吻合；多尺度模拟计算产生的伪速度与LBM 单尺度模拟结果基本相同，不会导致伪速度增加。这说明该方法在提高了计算效率的同时保证了计算的稳定性，验证了该多尺度模拟方法的准确性和高效性。通过免方程方法在气液两相分离过程中的应用研究，可为进一步从细微尺度出发对流动沸腾中气泡行为等复杂多相流过程的多尺度模拟奠定基础。

1 免方程多尺度方法

1.1 基本框架

免方程方法（EFM）建立了一种基于闭包（closure）的系统辨识，同时构建了微观/随机仿真和传统连续科学计算、数值分析的桥梁。目前免方程方法中常见的应用是时间尺度上的多尺度模拟，因此一般以时间尺度上的多尺度模拟为其基本框架。该基本框架由粗粒化时间步进（CTS）和相应的数值技术构成，其中CTS 相当于整个框架中的“内核”。在EFM 中，粗粒化时间步进包括“提升”（lifting，借助于适当的分布函数从宏观集中获得分子状态）、演化和“约束”（restriction，通过平均、筛选、光滑处理从微观或分子模型获得宏观状态集）3 个过程[6]。其中，提升过程是该组合中首先需实现的过程，它是一种跨尺度过程，能够把宏观系统量离散转化成与之相匹配的细小量离散分布，如在气体动态模拟中提升过程把某气体的密度离散成大量气体粒子的随机离散分布。演化过程把提升过程得到的细小量离散分布投入到细小尺度模型中进行运算，经过一些短的演化时间后从中得到新的细小量离散分布。在CTS 中演化不需要尺度跨越，整个过程都在微细尺度上完成。最后执行约束过程，其目的恰好与提升过程相反，即把新得到的细小量离散分布反馈到宏观水平。接下来把从连续数次CTS中得到的一系列宏观系统值抽离出来，运用合理的数值技术如Euler 法、Runge-Kutta 法、Newton- Raphson 法等对它们进行相应的数值处理。重复进行上述3 个过程，达到对系统分析研究的目的。其基本框架如图1所示。需要强调的是，免方程方法并不是一种具体的模拟方法，而是一种多尺度模拟框架。

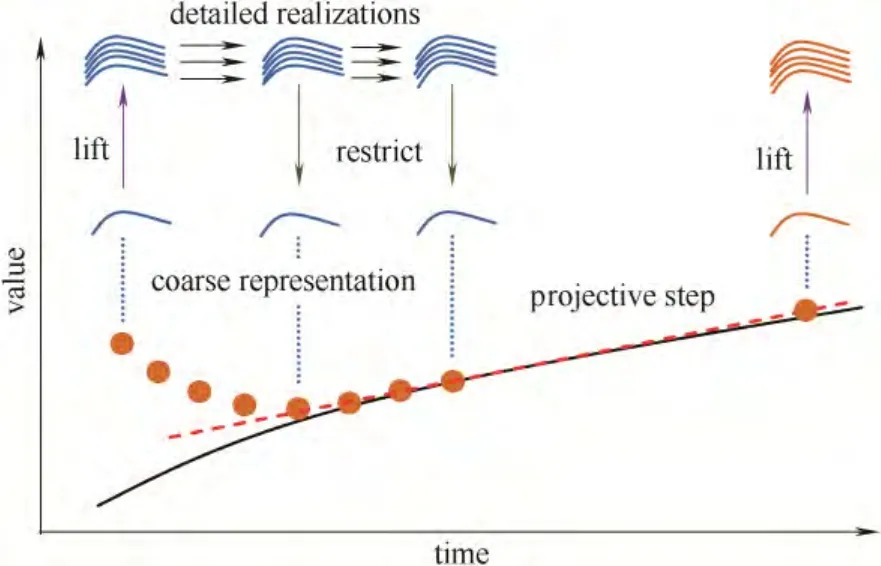
图1 基于EFM 的多尺度框架Fig.1 EFM-based multi-scale framework

1.2 粗粒化投影积分

粗粒化投影积分（CPI）是免方程方法中一种具有代表性的方法。其基本思想是在复杂系统的微细仿真器上运用传统的数值外推方法，达到对复杂系统进行分析研究的目的，即将粗粒化时间步进获取的宏观量实施外推投影以预测和捕获系统的特 性[15-17]。

这里简要说明CPI 的基本原理（图2）：假设模拟过程中的某一小段总共有n个连续演化步，当第1 步的初始宏观物理值提升至细微仿真器后，必须通过解析相对困难的细微仿真器依次计算这n个演化步，才能得到第n步的宏观物理值。这样虽然能计算出第n步的宏观值，但其运算效率低。而采用CPI 进行多尺度计算，则只需通过该细微仿真器计算出前k个演化步的宏观物理值，然后对这k个已获得的宏观物理值进行有效的外推处理，就能快速准确地预测出第n步的宏观值。由于中间省去了h（即n k- ）个演化步的计算量以及运用了较为准确的外推处理，CPI 能在保证系统模拟精度的同时有效地降低内存消耗，提高CPU 的计算效率。CPI 模拟全过程如图3所示。

图2 某一小段CPI 模拟过程Fig.2 CPI simulation diagram of a short part

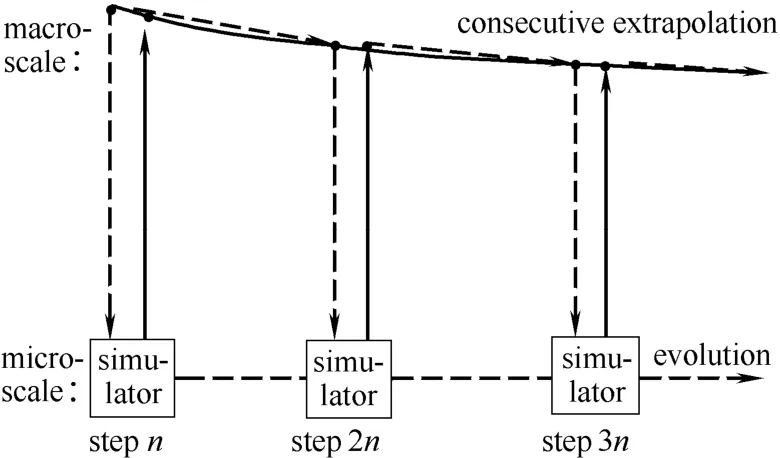
图3 CPI 模拟全过程Fig.3 Entire CPI simulation process diagram

由于CPI 无须获取系统的宏观模型方程，模拟研究是在现象及过程的细微仿真器上直接运用传统外推数值方法快速准确地预测系统的宏观性能，着 眼于过程细微尺度模型的多尺度模拟方法能更真实地反映实际过程的内在特性。本文应用伸缩式投影方法（TPM），选用具有二阶精度的Adams-Bashforth预测校正数值方法进行外推处理，其格式可表示为

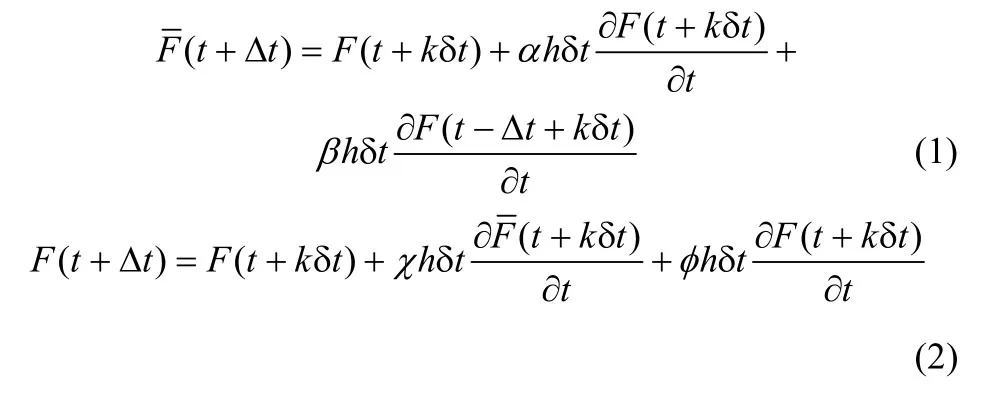
式中，F为变量的预报值，F为变量的校正值，k为演化数，h为投影数，α、β、χ、φ为Adams- Bashforth 方法中的二级系数,以下仿真计算中α取0.4，β取0.6，χ取0.3，φ取0.7。

2 基本模型

2.1 格子Boltzmann 模型

单组分多相LB 方程为[18-19]

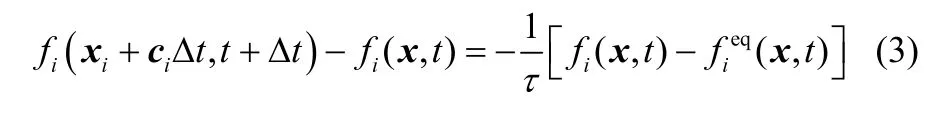
式中，x、t分别表示空间及时间坐标；i=0,1,2,…,b表示每个格点的不同离散速度方向；ci表示各个离散方向上的速度矢量；Δt表示格子离散的时间步长；τ为量纲1 松弛时间；为平衡态粒子分布函数。

由于D2Q9 模型比D2Q7 模型的数值稳定性好，本研究选取D2Q9 模型，因此Maxwell 平衡态分布函数为

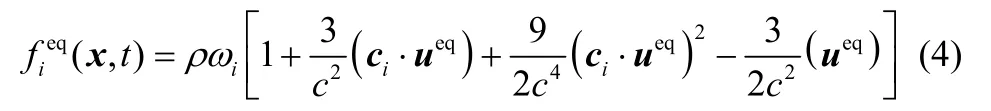
式中，权重系数ω0=4/9，ωi=1/9（i=1,2,3,4），1/36（i=5,6,7,8）；c=Δx/Δt为粒子迁移速度；equ为平衡态速度。密度和动量的宏观参数分别为

根据文献，要使气液两相分离，必须考虑相间相互作用力。Shan 和Chen 提出了一种能够直接刻画粒子间相互作用的LB 模型，即利用一个伪势函数来反映不同相之间的作用力

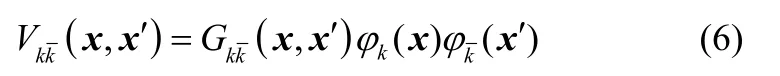
式中，ϕk(x)、分别是x处第k相和x′处第相的有效密度。若只考虑临近格点间的相互作用力，格林函数为

参数的绝对值决定了相间相互作用的强度，其符号决定二者之间是相互吸引还是相互排斥，Δx为格子长度。在由Shan 和Chen 提出的单组分多相LB模型中，位置x和位置x′的粒子之间的相互作用力为[13]

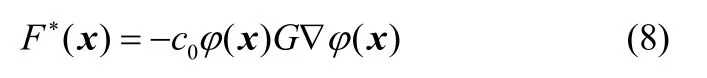
式中，c0为常数，对于D2Q9 格子模型c0=6.0。

Shan-Chen 伪势模型通过平衡态速度来体现相间作用力的影响，新的平衡速度为

2.2 提升算子和约束算子

结合LB 模型气液两相流动过程的演变规律，经过多次试验分析得到提升算子的具体形式

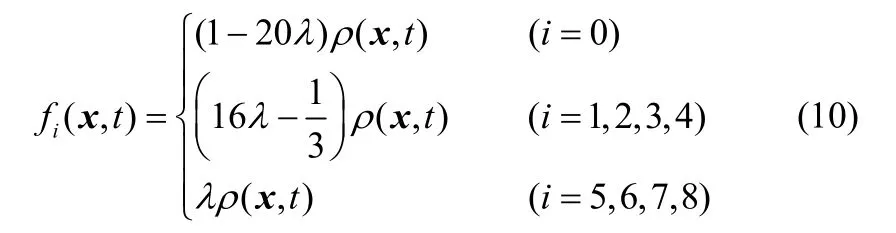
式中，1/48＜λ＜1/20。

约束算子则选取为LB 模型密度的宏观参数形式

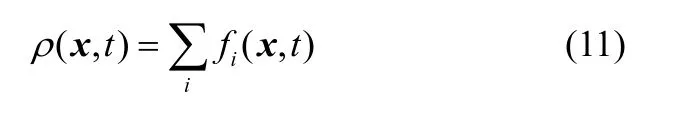
2.3 状态方程

粒子间相互作用力由式(8)给定，系统的状态方程可表示为[20]

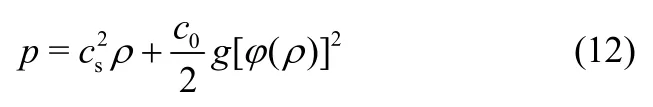
式中，cs为LB 模型的格子声速，对于D2Q9模型cs=1/。

本研究选取了以下3 种状态方程（equation of state，EOS）：van der Waals（vdW）状态方程，Redlich- Kwong（R-K）状态方程以及Peng-Robinson（P-R）状态方程。

vdW 状态方程

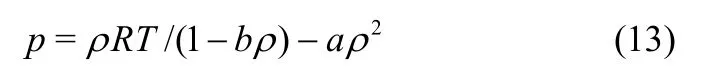
式中，R为通用气体常数，格子Boltzmann 方法中取值为1.0。压力对密度求一阶导数和二阶导数并令其等于零，则可得到临界点的数值：ρc=1/(3b)，Tc=8a/(27bR)。a和b为常量，它们分别取值a=9/49、b=2/21。

R-K 状态方程

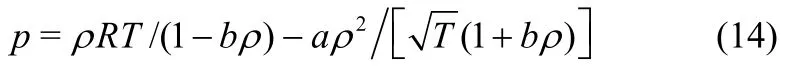
式中，a和b的值由临界参数表达：a=

P-R 状态方程

式中，a和b的值由临界参数表达：a=为偏心因子，与工质本身有关，水的偏心因子ω=0.344。

3 仿真结果与分析

本研究数值计算区域的格子划分为256×256，平衡态分布函数采用D2Q9 模型，松弛因子 1τ=，上下边界条件和左右边界条件均为周期性边界条件，伪势密度函数为任意常数。初始密度值ρ=ρc，为了使方程演化，在初始密度附近取0.01 的扰动。模拟结果均在以内存4GB、CPU 主频3.1GHz 的四核Xeon 处理器为计算平台的同一台计算机上运行得到。

3.1 不同状态方程的结果对比

图4给出了不同状态方程控制下LB 模型模拟所得的密度曲线与实验值的对比，图中的实验值根据水蒸气性质图表绘制得出，离散点为数值模拟计算得出的结果。通过对比可以发现，vdW 状态方程的温度取值范围最小，T/Tc取值范围约为[0.86，1.0]；P-R 状态方程的温度取值范围最大，约为[0.76，1.0]；R-K 状态方程中T/Tc取值范围约为[0.8，1.0]。在可取的温度范围内，vdW 状态方程控制下的模拟结果偏离实验值较多，密度相对误差较大，气相密度比实验值大，随着温度升高模拟结果与实验值的相对误差逐渐减小，而液相密度模拟结果比实验值小，与实验值的相对误差基本维持在13%左右。R-K 和P-R 状态方程模拟所得曲线与实验值吻合较好，对于气相密度R-K状态方程得到的结果与实验值最接近[图4(b)]，对于液相密度P-R 状态方程得到的结果较好。

图5和图6分别给出了vdW 和R-K、R-K 和P-R 状态方程控制下最大伪速度随密度比的变化曲线。通过对比可以看出，随着密度比的增大，各模型的最大伪速度均会增大。对于某一给定的密度比，R-K 模型的最大伪速度明显小于vdW 模型，而P-R 模型的最大伪速度小于R-K 模型；同时，P-R 模型密度比的取值范围最大，可以处理较高密度比的问题。综上所述，P-R 状态方程能较好地模拟水的相变过程。

图4 不同状态方程控制下的饱和密度曲线与实验值的对比Fig.4 Comparison of coexistence curves obtained from simulations with experimental values for different EOS

图5 vdW 和R-K 状态方程最大伪速度的变化曲线Fig.5 Maximum magnitude of spurious current changes with density ratio for vdW and R-K EOS

图6 R-K 和P-R 状态方程最大伪速度的变化曲线Fig.6 Maximum magnitude of spurious current changes with density ratio for R-K and P-R EOS

3.2 LBM 与TPM 模拟的对比

图7～图12给出了LBM 单尺度模拟与TPM 多尺度模拟在不同状态方程控制下所得结果的对比及其与实验值的对比。总计算步数为20000，此部分TPM 多尺度模拟选取的演化数和投影数均为400。

图7 vdW 模型的饱和密度曲线对比Fig.7 Comparison of coexistence curves for vdW EOS

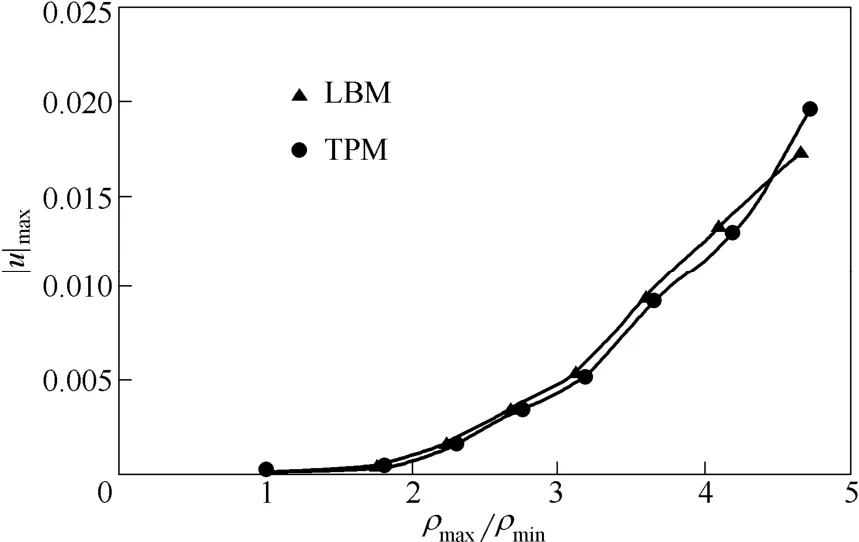
图8 vdW 模型最大伪速度对比Fig.8 Comparison of spurious current for vdW EOS

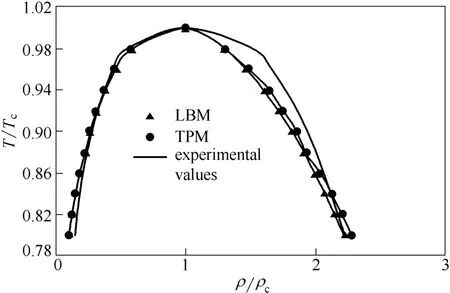
图9 R-K 模型的饱和密度曲线对比Fig.9 Comparison of coexistence curves for R-K EOS

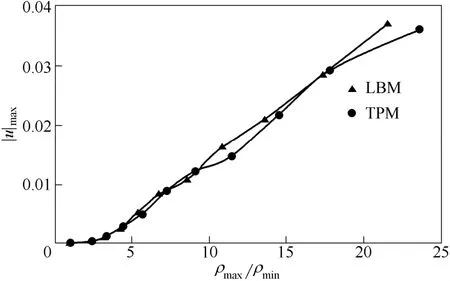
图10 R-K 模型最大伪速度对比Fig.10 Comparison of spurious current for R-K EOS

图11 P-R 模型的饱和密度曲线对比Fig.11 Comparison of coexistence curves for P-R EOS

图12 P-R 模型最大伪速度对比Fig.12 Comparison of spurious current for P-R EOS

由于vdW 状态方程本身形式简单，从图7可以看出vdW 模型的饱和密度曲线偏离实验值较大，但 其变化趋势与实验值保持一致。TPM 多尺度模拟结果与LBM 单尺度模拟结果十分接近，而且TPM 多尺度模拟结果比LBM 模拟结果更接近实验值。

图8给出了vdW模型最大伪速度随密度比的变化情况。可以看出，TPM 模拟产生的伪速度与LBM模拟产生的伪速度基本相同，TPM 模拟产生的伪速度除了最后一个点之外都比LBM 模拟小，说明采用此种情况下的TPM 多尺度模拟不会导致模型伪速度增大，保证了模型计算的稳定性。

图9给出了R-K 模型经过20000 步迭代后的饱和密度曲线。可以看出，TPM 多尺度模拟的结果与LBM 单尺度模拟的结果在气相部分吻合良好，而且与实验值十分接近；液相部分TPM 多尺度模拟结果比LBM 单尺度模拟结果更接近实验值。模拟结果比vdW 模型更加准确，模拟计算出的密度值准确性较好。在低温处，液相密度的相对误差小于2%；气相密度绝对误差很小，但相对误差较大。这是由状态方程的性质造成的，因为当温度远低于临界温度时密度比会变得很大。随着温度逐渐接近饱和温度，气相密度的相对误差从27%减小到7%。

图10给出了R-K 模型最大伪速度随密度比的变化趋势。可以看出，TPM 多尺度模拟结果与LBM单尺度模拟结果基本保持一致，TPM 产生的伪速度平均值小于LBM 单尺度模拟产生的伪速度平均值，说明采用此种情况下的TPM 多尺度模拟降低了模型的伪速度，提高了模型的稳定性。

图11给出了P-R 模型经过20000 步迭代后的饱和密度曲线。可以看出，TPM 多尺度模拟结果与LBM 单尺度模拟结果十分吻合，气液两相的密度变化趋势与实验值较为接近，但P-R 模型产生的误差比R-K 模型产生的误差大。在低温处，液相密度的相对误差小于10%；但气相密度相对误差还是较大，尽管绝对误差很小。

图12给出了P-R 模型最大伪速度随密度比的变化趋势。可以看出，P-R 模型的密度比变化范围比R-K 模型大，能处理高密度比情况下的问题。TPM 多尺度模拟的伪速度小于LBM 单尺度模拟的伪速度，说明此种情况下采用TPM 多尺度模拟不仅没有导致模型的伪速度增大，反而降低了模型的伪速度，提高了模型的稳定性，充分体现了该多尺度模拟方法的有效性。

3.3 不同投影步数的模拟结果对比

改变投影和演化的步数，分别选取演化400 步、投影400 步（TPM1），演化200 步、投影600 步（TPM2），演化100 步、投影700 步（TPM3），演化100 步、投影1900 步（TPM4），其他计算条件不变，比较TPM 多尺度模拟在不同投影情况下的模拟结果。

图13～图18给出了选取不同的投影步长时3种状态方程控制下取得的模拟结果。

图13和图14为vdW 状态方程控制下的模拟结果。可以看出，当投影步数分别取值400、600、700和1900 时，TPM 多尺度模拟与LBM 单尺度模拟所得饱和密度曲线基本重合。投影数为400、600 和700 时，模型的最大伪速度保持一致；投影数为1900时，模型的最大伪速度有所增大。

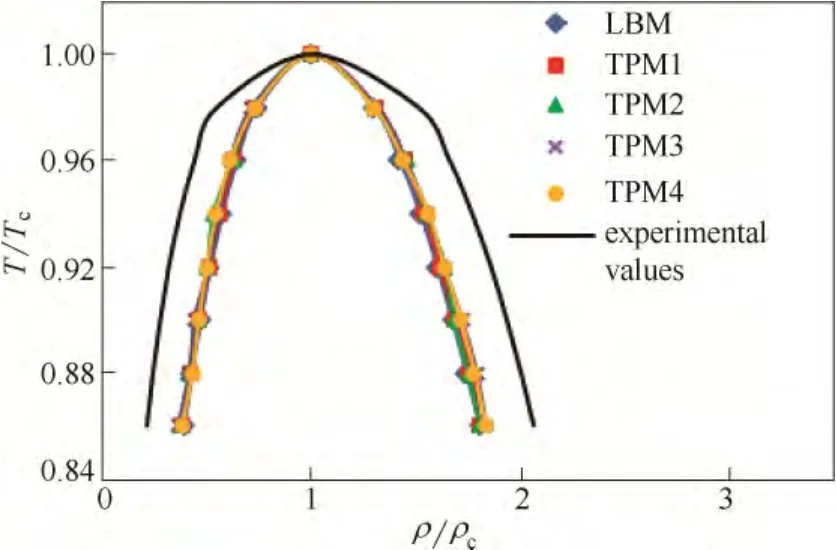
图13 不同投影步数下vdW 模型的饱和密度曲线对比Fig.13 Comparison of coexistence curves obtained from simulations using different extrapolation steps with experimental values for vdW EOS

图14 vdW 模型最大伪速度的变化曲线对比Fig.14 Comparison of spurious current obtained from simulations using different extrapolation steps for vdW EOS

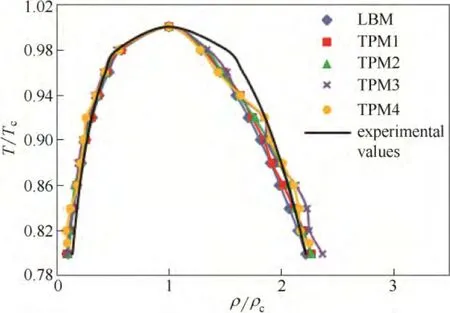
图15 不同投影步数下R-K 模型的饱和密度曲线对比Fig.15 Comparison of coexistence curves obtained from simulations using different extrapolation steps with experimental values for R-K EOS

图15和图16为R-K 状态方程控制下的模拟结果。可以看出，几种情况下的TPM 多尺度模拟与LBM 单尺度模拟所得饱和密度曲线在气相区域基本重合。在液相区域，投影步数为400 和600 时所得结果比LBM 单尺度模拟更接近实验值，TPM 与LBM 模拟的最大伪速度基本相同；投影数为700 时，模拟结果在低温部分与实验值的偏差增大，模型的最大伪速度稍有增大；投影数为1900 时，模拟结果在低温部分与实验值最为接近，模型的伪速度与其他几种情况基本相同。

图16 R-K 模型最大伪速度的变化曲线对比Fig.16 Comparison of spurious current obtained from simulations using different extrapolation steps for R-K EOS

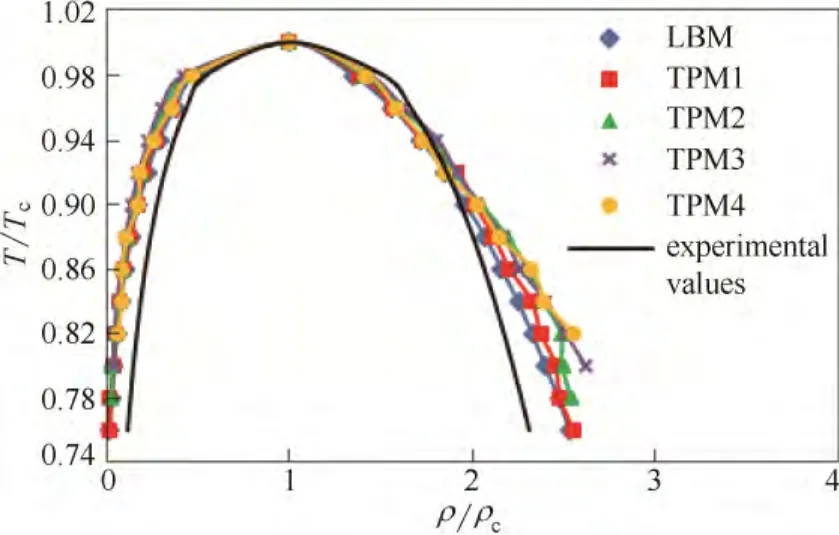
图17 不同投影步数下P-R 模型的饱和密度曲线对比Fig.17 Comparison of coexistence curves obtained from simulations using different extrapolation steps with experimental values for P-R EOS

图18 P-R 模型最大伪速度的变化曲线对比Fig.18 Comparison of spurious current obtained from simulations using different extrapolation steps for P-R EOS

图17和图18为P-R 状态方程控制下的模拟结果。可以看出，TPM 多尺度模拟与LBM 单尺度模拟所得饱和密度曲线在气相区域基本重合。在液相区域，TPM 多尺度模拟比LBM 单尺度模拟所得曲线在低温部分与实验值的偏差增大。当选取700 和1900 的投影步长时，TPM 模拟的温度取值范围减小，而最大伪速度与LBM 模拟结果基本保持一致，投影步长为1900 的伪速度稍大。

在模拟精度和运算效率方面，以R-K 模型为例（见表1和表2）。由表1可以看出，对于气相密度，TPM 多尺度模拟的平均误差和均方根误差都大于LBM 模拟的误差。当投影步数为400、600 和700时，气相密度的平均误差随投影步长增大而增加；继续增大投影步数至1900 时，相对误差的平均值并没有增大，而是保持为15%。液相密度方面，除投影步数为400 的情况之外，TPM 模拟的相对误差均比LBM 单尺度模拟的相对误差小；平均误差最小为4.0%，分别是投影步数为600 和1900 时取得的。而从液相的均方根误差可以看出，TPM 多尺度模拟的误差（10%左右）均小于LBM 单尺度模拟的误差（12.2%），说明TPM 多尺度模拟在这一部分有效地提高了模型的准确性。由表2可以看出，TPM多尺度模拟的CPU 耗时明显小于LBM 单尺度模拟的CPU 耗时，可见TPM 多尺度模拟能够大大提高模型的运算效率；同时，由总体误差可以看出TPM多尺度模拟的误差均小于LBM 单尺度模拟的误差，充分说明了该方法能够在提高运算效率的同时提高模型的精确度，体现了其在复杂计算中的优势。当投影步数从700（TPM3）增大至1900（TPM4）时,误差保持在8%左右，体现了该方法在相当范围内的稳定性。

综上所述，在合理的投影范围内运用TPM 多尺度模拟方法对气液两相分离过程进行模拟研究能够大幅降低对细微仿真器的依赖性，说明所提多尺度模拟方法对现阶段细微单尺度模拟中出现的巨大内存开销和CPU 耗时问题实现了实质性的解决，体现了其有效性和高效性。当在细微尺度上模拟更复杂的气液两相流动过程或更复杂的多尺度系统时，采用该多尺度方法能有效地解决细微单尺度模拟难以实现的难题，从而为复杂两相流动传热问题的模拟研究提供新思路。

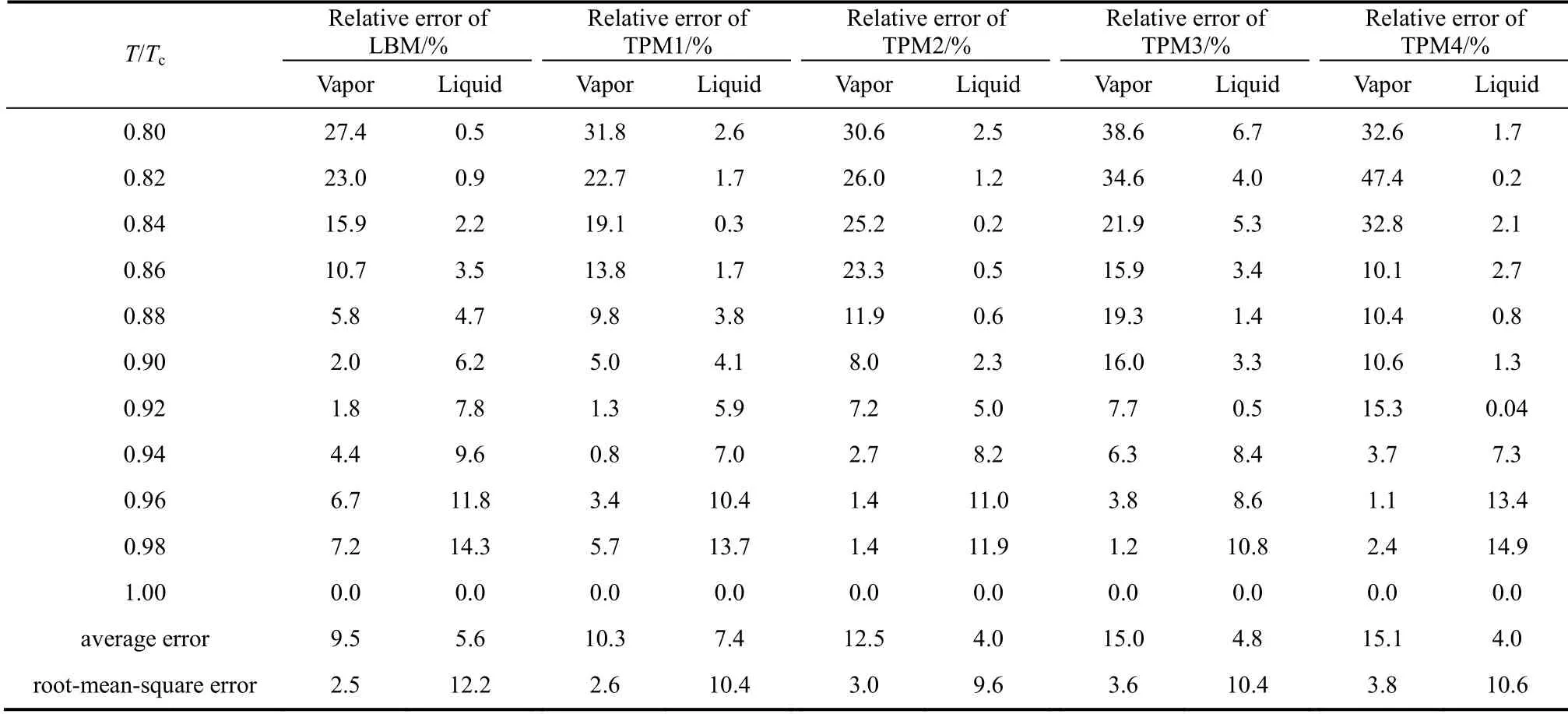
表1 LBM 和TPM 模拟与实验值的误差Table 1 Error of simulation results obtained from LBM and TPM model verified by experimental values

表2 模拟运算效率Table 2 Operational efficiency of simulations

4 结 论

本研究提出了一种用于模拟气液两相分离的免方程多尺度模拟方法，该方法以气液两相的格子Boltzmann（LB）模型作为介观仿真器，LB 模型进行少量演化步后，运用二阶伸缩式投影方式对介观仿真演化得到的气液相密度进行有效的外推处理，能够快速准确地获取后续演化步的信息，从而实现对气液两相分离过程的多尺度模拟研究。

对气液两相分离过程中密度分布和模型产生的伪速度的仿真分析表明，本研究所提出的多尺度模拟方法从介观尺度出发真实地反映了气液两相分离的过程，在确保多尺度模拟的准确性和真实性的基础上有效地解决了细微尺度模拟中出现的CPU耗时过长、内存开销过大的问题。与以往的LBM单尺度模拟相比，本研究所提出的多尺度模拟方法具有明显的计算优势以及多尺度特点，说明所提方法对于研究更为复杂的流动传热问题非常具有潜力。通过EFM 方法的改进以及LBM 模型本身的改进，可为下一步工作实现流动沸腾中气泡动力学行为等更复杂和更深层次的两相流动传热过程的数值模拟研究打下坚实的基础。另外，将该方法的理念运用于其他能源动力系统的模拟也是重要的发展方向，以进一步推动多尺度模拟的研究和发展。

符 号 说 明

a，b——状态方程中的系数

c——粒子迁移速度

ci——离散方向上的速度矢量

cs——LB 模型的格子声速

F——变量的校正值

F——变量的预报值

F∗——粒子间相互作用力

fi——粒子分布函数

——平衡态粒子分布函数

——格林函数

h——伸缩式投影方法的微观投影数

i——离散速度方向

k——伸缩式投影方法的微观演化数

p——压力

R——通用气体常数

T——温度

t——时间坐标

Δt——格子离散的时间步长

δt——伸缩式投影方法的微观演化步长

u——宏观速度

——平衡态速度

——伪势函数

x——空间坐标

Δx——格子离散的空间步长

α，β，χ，ϕ——Adams-Bashforth 方法中的系数

λ——提升算子中的系数

ρ——宏观密度

τ——量纲1 松弛时间

φ——有效密度

ω——偏心因子

ωi——权重系数

[1]Guo Zhaoli (郭照立),Zheng Chuguang (郑楚光),Li Qing (李青),Wang Nengchao ( 王能超).Lattice Boltzmann Method for Hydrodynamics (流体动力学的格子 Boltzmann 方法)[M].Wuhan:Hubei Science & Technology Press,2002:158.

[2]He Yaling (何雅玲),Wang Yong (王勇),Li Qing (李庆).Lattice Boltzmann Method:Theory and Applications (格子Boltzmann 方法的理论及应用) [M].Beijing:Science Press,2008:156.

[3]Zeng Jianbang (曾建邦),Li Longjian (李隆键),Liao Quan (廖全),Chen Qinghua (陈清华),Cui Wenzhi (崔文智),Pan Liangming (潘良明).Application of lattice Boltzmann method to phase transition process [J].Acta Physica Sinica(物理学报),2010,59 (1):178-185.

[4]Deen N G,van Sint Annaland M,Kuipers J A M.Multi-scale modeling of dispersed gas-liquid two-phase flow [J].Chemical Engineering Science,2004,59 (8):1853-1861.

[5]Armaou A,Kevrekidis I G,Theodoropoulos C.Equation-free gaptooth-based controller design for distributed complex/multiscale processes [J].Computers & Chemical Engineering,2005,29 (4):731-740.

[6]Kevrekidis I G,Gear C W,Hyman J M,Kevrekidis P G,Runborg O,Theodoropoulos C.Equation-free coarse-grained multiscale computation:enabling microscopic simulators to perform system-level analysis [J].Communications in Mathematical Sciences,2003,1 (4):715-762.

[7]Kevrekidis I G,Gear C W,Hummer G.Equation-free:the computer-aided analysis of complex multiscale systems [J].AⅠChE Journal,2004,50 (7):1346-1355.

[8]Gear C W.Projective integration methods for distributions [J].NEC Trans.,2001,130:1-9.

[9]Gear C W,Kevrekidis I G.Projective methods for stiff differential equations:problems with gaps in their eigenvalue spectrum [J].SⅠAM Journal on Scientific Computing,2003,24 (4):1091-1106.

[10]Cisternas J,Gear C W,Levin S,et al.Equation-free modelling of evolving diseases:coarse-grained computations with individual-based models [J].Proceedings of the Royal Society of London.Series A:Mathematical,Physical and Engineering Sciences,2004,460 (2050):2761-2779.

[11]Makeev A G,Kevrekidis I G.Equation-free multiscale computations for a lattice-gas model:coarse-grained bifurcation analysis of the NO + CO reaction on Pt (100) [J].Chemical Engineering Science,2004,59 (8):1733-1743.

[12]Erban R,Kevrekidis I G,Adalsteinsson D,et al.Gene regulatory networks:a coarse-grained,equation-free approach to multiscale computation [J].Journal of Chemical Physics,2006,124 (8):084106.

[13]Kevrekidis I G,Samaey G.Equation-free multiscale computation:algorithms and applications [J].Annual Review of Physical Chemistry,2009,60:321-344.

[14]Zeng Jianbang (曾建邦),Li Longjian (李隆键),Liao Quan (廖全),Cui Wenzhi (崔文智),Chen Qinghua (陈清华),Pan Liangming (潘良明).Simulation of boiling process with lattice Boltzmann method [J].Journal of Xi’an Jiaotong University(西安交通大学学报),2009,43 (7):25-29.

[15]Maluckov A M,Ishiguro S,Škoric M M.A macro projective integration method in 2D microscopic system applied to nonlinear ion acoustic waves in a plasma [J].Communications in Computational Physics,2008,4 (3):556-574.

[16]Gear C W,Li J,Kevrekidis I G.The gap-tooth method in particle simulations [J].Physics Letters A,2003,316 (3):190-195.

[17]Yang Chen (杨晨),Peng Wei (彭伟).Telescoping projective methods for the multiscale simulation of reaction-diffusion processes [J].Journal of Engineering Thermophysics(工程热物理学报),2011,32 (3):377-381.

[18]Shan X,Chen H.Lattice Boltzmann model for simulating flows with multiple phases and components [J].Physical Review E,1993,47 (3):1815.

[19]Shan X,Chen H.Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation [J].Physical Review E,1994,49 (4):2941.

[20]Yuan P,Schaefer L.Equations of state in a lattice Boltzmann model [J].Physics of Fluids(1994-present),2006,18 (4):42101.