基于三角区间软约束的模型预测控制算法
2015-08-21孙超戴睿郝晓辰刘彬周湛鹏
孙超,戴睿,郝晓辰,刘彬,周湛鹏
(燕山大学电气工程学院,河北 秦皇岛 066004)
引 言
模型预测控制(MPC)[1-2]是一类产生于工业控制实践的计算机控制算法。作为先进控制技术的典型代表,由于具有建模容易、鲁棒性好、约束处理灵活等优点,而被广泛地应用于石油、化工等工业过程[3-5]。在实际工业过程应用中,MPC 对被控变量(CV)的控制方式主要有设定值控制(set point control)和区间控制[6-7](interval control)两种。设定值控制可以将CV 控制在理想的目标值,适用于具有严格控制指标的CV,但其又有自由度低、鲁棒性差的缺点,特别体现在遇到工业扰动时的控制性能会严重下降,使得CV 产生剧烈波动,影响产品质量[8-10]。相比之下,区间控制系统具有自由度高、鲁棒性好等优点,近年来代替设定值控制成为各界研究的重点。文献[11]提出一种“软约束”处理方法改善控制品质,实现区间控制。文献[12]提出了一种稳定的区间MPC 控制器,该方法的代价函数中包含了输入输出的稳态经济目标,由于考虑了零值控制器,所以此控制器并不能达到局部最优。文献[13]用一种稳态区间可操作性方法设计了基于模型的约束控制器,可用来处理输入个数少于输出的多变量的非方系统,不过,此方法中输入集合与输出集合的兼容性容易出现问题。上述文献均是采用包含理想目标值在内的区间范围来代替确定的理想目标值,在CV 进入区间后,将不再进行控制作用,CV 可能运行在区间内的任意位置而非理想目标值。这些方法虽然提高了系统的鲁棒性和自由度,却并没有对设定值控制的性能做进一步优化,解决设定值控制鲁棒性差、自由度低的缺点。
为解决上述问题,本文兼顾设定值控制和区间控制各自的优势,基于动态矩阵控制(DMC)[14-15],提出一种三角区间软约束模型预测控制算法。算法根据工业过程实际要求,设置容忍区间及理想目标值,并以此确定三角区间,目的是优先将CV 控制在三角区间中,再对CV 进行动态优化,逐步将CV控制到理想的目标值,与此同时,又增加了系统的自由度,保证一定的鲁棒性。最后,通过对Shell公司的典型重油分馏塔进行仿真实验,验证了算法的有效性及可行性。
1 三角区间软约束模型预测控制算法研究
实际工业过程中,对具有严格控制指标的CV往往采用设定值控制,以期望将CV 稳定在某一理想值。但是,传统设定值控制的自由度低、鲁棒性差,特别是在系统受到扰动时,系统的动态性能会严重下降[16-17]。因此,在设定值控制的基础上,加入三角区间软约束,使CV 到目标值的控制分解为两个阶段。第一阶段是令受干扰后的CV 进入到所设置的区间内,第二阶段是在区间内将CV 进一步控制到目标值。通过这种方法来减小目标函数求解的误差,提高系统的自由度和鲁棒性。
1.1 三角区间软约束的设计
根据工业流程控制的工艺,确定控制过程中第一阶段的控制目标,即将CV 控制在包含理想值的区间内。当CV 被控在此区间内时,可以保证系统的稳定运行及产品的质量,称此区间为容忍区间(tolerance range)。
如图1所示,yc为预测输出,ymax、ymin为容忍区间的上下界,yH、yL为三角区间的上下界,ysp为目标值。ε为表征预测值超出三角区间程度的变量。P为预测时域,yH、yL分别由k时刻容忍区间的上下界与k+P时刻的目标值相连获得。从图中可以看出,三角区间的上下界可以用几何关系求出
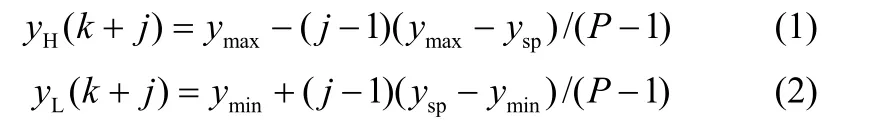
其中,1,,jP=… 。由式(1)、式(2)可知,当ymax、ymin和ysp设置完成后,yH和yL与预测时域P的值有关,一旦P值确定,yH和yL在各个预测时刻的值也被确定。除非为了改变控制策略而改动了已设置参数的值,否则yH和yL的值在滚动优化的过程中将不再改变。

图1 三角区间设置示意图Fig.1 Triangular interval setting diagram
由此,可以得到k时刻优化变量ε的表达式

其中,j=1,…,P。由式(3)可以看出,当Yc在三角区间外时,ε表示Yc到最近的三角区间界限的距离。而当Yc在三角区间内部时,ε的值恒为零。以优化变量 ε(k) 构成三角区间软约束(triangle interval soft constraint,TISC),并加入到目标函 数中。
1.2 目标函数的设计
当CV 受到扰动时,导致输出值严重偏离了目标值,且超出了三角区间,这时希望控制器能够对预测值进行一个强的惩罚,使预测值快速地回到三角区间,当预测值进入三角区间后,再通过设定值控制把预测值逐步控制到目标值上。
根据这一控制思路,提出如下的优化性能指标
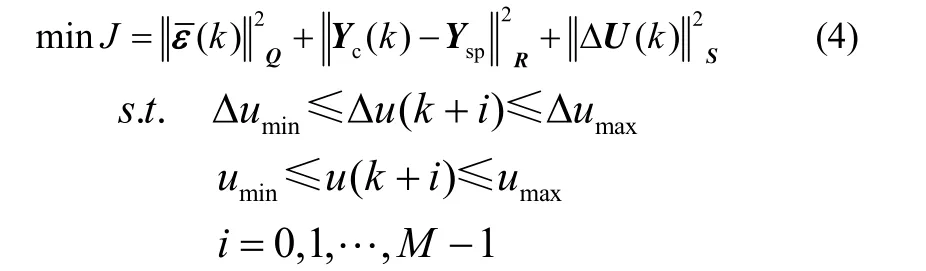
其中

Yc(k)为k时刻的预测值,Q、R、S为各项的权值矩阵,M为控制时域,目标函数的第1 项是三角区间软约束项,第2 项为设定值控制项,第3 项则是为了防止控制增量变化太过剧烈MV 软约束 项[18]。
由目标函数可以看出,本文所提算法与设定值控制及区间控制是有密切联系的,通过权值的调节也可以看出这一点。当权值矩阵Q的值全为零时,即相当于消去三角区间软约束项,此时将只进行设定值控制。同理,当权值矩阵R的值全为零时,将只进行三角区间控制。
1.3 三角区间软约束MPC 算法
假设被控对象为开环渐进稳定系统,且有m个输入,p个输出。将本文设计的三角区间软约束与DMC 相结合,并应用于此被控对象,给出三角区间软约束MPC 算法的流程。
1.3.1 预测模型 若已测得每个输出yi对每一输入uj的阶跃响应aij(t),则可由它们在采样点上的值组成模型向量
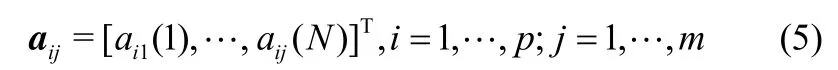
式中,N为建模时域。
1.3.2 输出预测 取预测时域为P,控制时域为M,则yi的模型预测输出为

式中


将多变量系统预测输出写为矩阵形式
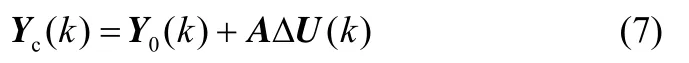
其中

为了减小实际控制过程中存在的干扰及模型失配对预测输出造成的影响,采用当前时刻模型输出与系统的实际输出的差值对预测输出进行修正

其中,ei(k)=y i(k) -yci(k|k)为当前时刻模型输出与系统的实际输出的差值。为误差校正矩阵。
1.3.3 目标函数的求解
①Yc在三角区间内时=0,则目标函数化为
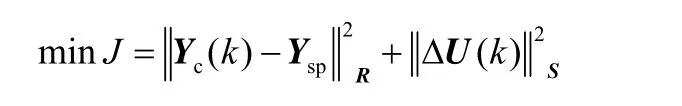
显然,此时的目标函数仅是设定值控制的表达形式,属于标准的二次规划问题。
②Yc在三角区间上方时=Yc-YH,则
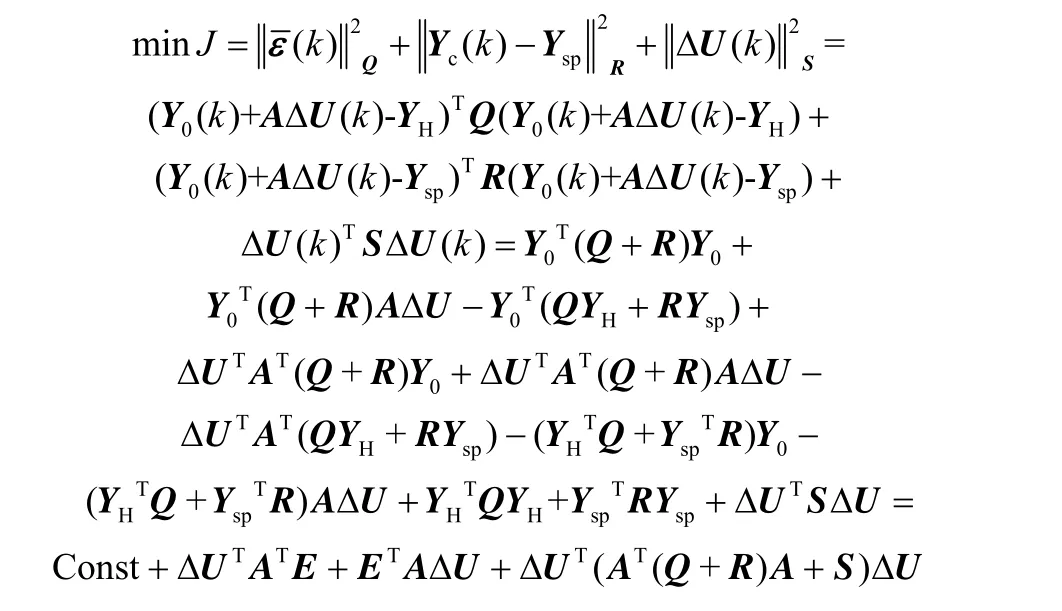
即

其中,E=Q(Y0-YH) +R(Y0-Ysp)为对角阵,F=AT(Q+R)A+S,Const 为已知的系数矩阵运算式,对目标函数的求解并没有影响。因此,此时的目标函数是二次规划问题。
③Yc在三角区间下方时ε(k)=YL-Yc,与情形②类似,此时目标函数也是二次规划问题。
综上所述,无论Yc取值如何,此目标函数均属于二次规划问题,可采用序列二次规划(SQP)[19]算法求取最优控制增量序列ΔU(k),仅选取第1 项作为当前时刻的控制增量,与 (1)u k- 叠加得到当前时刻的控制量。通过滚动优化,即可求得各个时刻的最优控制量。
1.4 参数对算法性能的影响
1.4.1 容忍区间上下界ymax、ymin根据实际被控系统的特点选定预测时域P之后,若容忍区间上下界ymax、ymin确定,则三角区间yH、yL也被确定。三角区间yH、yL体现了区间控制与设定值控制之间的联系,容忍区间越大,三角区间的开口越大,给予控制器的自由度也越高,控制的鲁棒性也随之上升。而容忍区间越小,整个算法也更接近于设定值控制的效果,极限情况下,令yH与yL均取目标值,此时算法已相当于设定值控制。
1.4.2 目标函数中的权值Q、R、S权值S的主要作用在于防止控制量过于剧烈的变化。权值Q主要体现了三角区间软约束项的控制力度。R则体现了设定值控制的控制力度。Q和R的比例关系也决定了控制的效果。Q越大,三角区间控制力度越大,鲁棒性越好,但达到目标值的速度会减慢。R越大,设定值控制力度越大,但鲁棒性会变差,输出的波动也会增多。考虑极限情况,Q=0 时,相当于只进行设定值控制,控制器的自由度最小,鲁棒性最差。当R=0 时,相当于只进行三角区间控制,由于三角区间是一束口区间,最终预测值将会在预测步数P时达到目标值,此时控制器的自由度最大,MV 会有最小的偏移量及对模型最小的敏感性。因此,为了保证算法的有效性,应保证 ≫Q R。
2 三角区间软约束MPC 算法的鲁棒性性能分析
在无约束或非起作用约束时,对目标函数的推导式(9)使用二次规划求解

令=-ATE,X=ΔU,则式(10)可以转化为标准的数学方程组形式

由于实际问题中的初始数据会有误差,即有扰动,这将会影响到计算的结果,产生误差。在式(11)中,系数矩阵F=AT(Q+R)A+S,主要反映了动态矩阵A对方程组解的影响,即模型失配问题。而=-ATE=-AT[Q(Y0-YH) +R(Y0-Ysp)]主要反映了输出值与控制目标的偏差,即系统抗干扰的问题。
定义1当一个方程组,由于系数矩阵或者右端的微小扰动而引起解发生巨大变化时,称该方程组是“病态”的。
定义2对非奇异矩阵F,称数为矩阵F的条件数,记为

引理[20]由于条件数的直接求解困难,根据工程实践经验,可判断方程组在下列情况下是病态的:
① 用主元素法时出现小主元;
② 系数矩阵中有行(或列)近似线性相关,或者系数行列式的值近似为零。
定理设X和X∗是方程组(11)的准确解和近似解,r为∗X偏差,则

证明:由方程组(11)可得
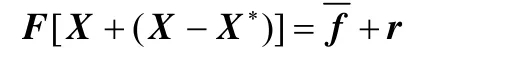
由FX=f,得F(X-X∗)=r,从而有
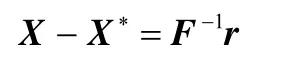
两边取范数,得
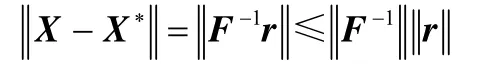
所以

证毕。
由式(13)可以看出,当方程组“病态”严重时,条件数很大,即使偏差很小,解的相对误差仍可能很大。反之,若可以减少偏差,则解的相对误差将会缩小,系统的鲁棒性将会显著提升[21]。
图2中,d表示预测值到目标值的偏差,其他与图1所示变量一致。在求解目标函数(9)时,有系数矩阵F=AT(Q+R)A+S。若F中含有高度关联的变量时,此时的条件数会很大,即是“病态”的,此时目标函数的解对模型误差是敏感的。
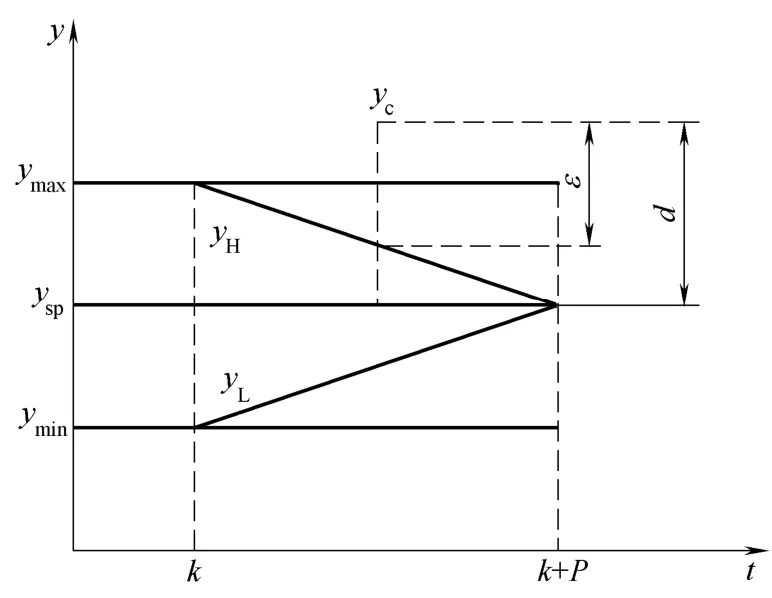
图2 两种算法的预测值偏差对比Fig.2 Contrast between deviation of two algorithms
如图2所示,当系统受到扰动时,Yc在三角区间外,此时Yc与目标值的偏差d较大,则=-ATR(Y0-Ysp)=-ATR⋅。由于F是“病态”的,模型误差将被放大。由式(13)可知,较大的偏差会使解的误差增大,控制器必须利用相互抵消的MV 移动的作用来使预测值达到特定的值,这时控制器需要频繁的变动且输出值的波动会十分剧烈,这样显然更容易引起控制的不稳定。
设置三角区间后,Yc到三角区间上界的偏差为ε,令 ≫Q R,则

由图2可知ε<d,故f2<f1,减小了方程(11)右端的偏差。而减小偏差会使解的误差显著缩小,MV 会以更小的移动来使Yc进入三角区间内,而不会引入过大的瞬态偏差,防止输出的剧烈波动。在Yc进入三角区间后,由式(3)可知,此时 0ε=,三角区间软约束项不再起惩罚的作用,设定值控制项的作用得以体现。由于预测值已经很接近目标值,此时控制器确定的轨迹会使MV 有更小的偏移量并且对模型误差更小的敏感性。Yc进入三角区间后的设定值控制过程中,即使预测值会产生一些波动,也只是在容忍区间内发生,这在工程实际中是被允许的。
3 实验仿真分析
3.1 实验仿真
为验证本文所提算法的可行性及有效性,采用Shell 公司的典型重油分馏塔进行仿真实验。该模型是一个三入三出的线性系统,传递函数矩阵为

u1、u2、u3为MV,约束区间为[-0.5,0.5],y1、y2、y3为CV,控制目标为:y1=0,y2=0.3,为保证控制问题有可行解,y3采用区间控制,目标区间为[-0.3,0]。采用阶跃函数模拟扰动的影响,初始时刻y1、y2均偏离了目标值,且=1.0,=0.4。取预测时域为24,控制时域为10,y1、y2的容忍区间分别为[-0.2,0.4],[0.1,0.4]。为突出本文所提算法的优势,与设定值控制进行了对比,为增加可比性,使两者的权值矩阵保持相等。由于区间控制只是把CV 控制在区间内任意位置,并不能实现定值控制,故不作对比。
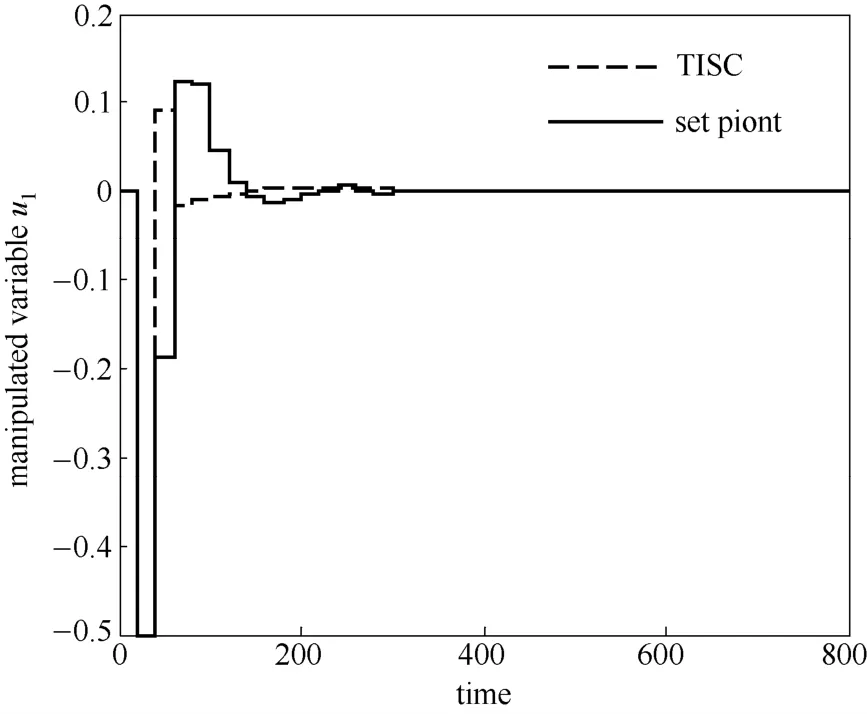
图3 控制增量u1 变化曲线Fig.3 Change curve of control increment u1

图4 控制增量u2 变化曲线Fig.4 Change curve of control increment u2
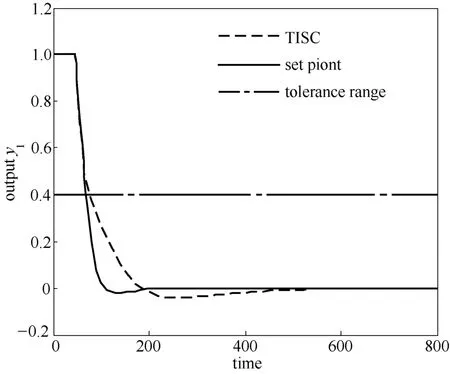
图5 实际输出y1 变化曲线Fig.5 Change curve of actual output y1

图6 实际输出y2 变化曲线Fig.6 Change curve of actual output y2

图7 实际输出y3 变化曲线Fig.7 Change curve of actual output y3
3.2 仿真结果分析
由仿真结果可以看出,系统在受到干扰后,设定值控制下的输出曲线y1可以更快达到目标值,且波动较小,但是输出曲线y2的性能质量却很差,输出波动频繁且剧烈,三次超出系统的容忍区间,显然这对系统整体的稳定运行是不利的。这是因为在外界干扰作用下,y1、y2产生了瞬时偏差,远离了目标值,由鲁棒性分析可知,较大的偏差会使解的误差增大,控制器必须利用相互抵消的MV 移动的作用来使预测值达到目标值。又由于y1的偏差较y2更大,为保证y1迅速达到目标值,使得控制器动作频繁且动作幅度大,控制器的自由度低,已没有更多的自由度保证输出曲线y2的性能质量,说明此时系统的鲁棒性很差。
而在三角区间软约束预测控制算法的控制下,输出曲线y1虽然延长了到达目标值的时间,但可以快速进入容忍区间且变化更加平缓。同时,输出曲线y2输出波动及超出容忍区间次数减少,曲线也更加平缓。这是因为设置三角区间后,瞬时偏差减小,控制器求解的误差减小,因而降低了控制器动作的频率和幅度,增加了控制器的自由度与鲁棒性。显然,三角区间软约束预测控制算法较设定值控制有更好的整体性能。
4 结 论
石油、化工等实际工业控制过程中,对具有严格控制指标的CV 往往采用设定值控制,但其又有自由度低、鲁棒性差的缺点。为解决这一问题,本文提出了三角区间软约束模型预测控制算法。仿真结果表明,本文算法综合了设定值控制与区间控制各自的优势,在三角区间软约束的作用下,保证了CV 可以运行在理想目标值的同时,又最大限度地保证了系统的鲁棒性和自由度,提高了系统对干扰的应对能力,控制效果明显优于设定值控制。因此,三角区间软约束模型预测控制算法更好地符合了实际工业生产中对某些CV 进行定值控制的要求。
[1]Qin S J,Badgwell T A.A survey of industrial model predictive control technology [J].Control Engineering Practice,2003,11 (7):733-764.
[2]Ferramosca A,Limon D.MPC for tracking zone regions [J].Journal of Process Control,2010,20 (4):506-516.
[3]Maldonado M,Desbiens A,del Villar R.Potential use of model predictive control for optimizing the column flotation process [J].Ⅰnternational Journal of Mineral Processing,2009,93 (1):26-33.
[4]Cristea M V,Agachi S P,Marinoiu V.Simulation and model predictive control of a UOP fluid catalytic cracking unit [J].Chemical Engineering and Processing,2003,42 (2):67-91.
[5]Zou Tao (邹涛),Wang Dingding (王丁丁),Pan Hao (潘昊),Yuan Mingzhe (苑明哲),Ji Zhongwan (季忠宛).From zone model predictive control to double-layered model predictive control [J].CⅠESC Journal(化工学报),2013,64 (12):4474-4483.
[6]Rishi Amrit,James B Rawlings,David Angeli.Economic optimization using model predictive control with a terminal cost [J].Annual Reviews in Control,2011,35 (2):178-186.
[7]John M Carson Ⅲ,Behçet Açıkmeşe,Richard M Murray,Douglas G MacMartin.A robust model predictive control algorithm augmented with a reactive safety mode [J].Automatica,2013,49 (5):1251-1260.
[8]Jin Xin (金鑫),Chi Qinghua (池清华),Liu Kangling (刘康玲),Liang Jun (梁军).Disturbance rejection constraints generalized predictive control of diagonal CARIMA model [J].CⅠESC Journal(化工学报),2014,65 (4):1310-1316.
[9]Zhang Bin,Yang Weimin,Zong Hongyuan,Wu Zhiyong,Zhang Weidong.A novel predictive control algorithm and robust stability criteria for integrating processes [J].ⅠSA Transactions,2011,50 (3):454-460.
[10]Huang He,Li Dewei,Lin Zongli,Xi Yugeng.An improved robust model predictive control design in the presence of actuator saturation [J].Automatica,2011,47 (4):861-864.
[11]Xu Zuhua,Zhao Jun,Qian Jixin.Zone Model predictive control algorithm using soft constraint method [J].Machine Tool & Hydraulics,2004,12 (3):106-108.
[12]González A H,Odloak D.A stable MPC with zone control [J].Journal of Process Control,2009,19 (1):110-122.
[13]Lima F V,Georgakis C.Design of output constraints for model-based non-square controllers using interval operability [J].Journal of Process Control,2008,18 (6):610-620.
[14]González A H,Marchetti J L,Odloak D.Robust model predictive control with zone control [J].ⅠET Control Theory and Applications,2009,3 (1):121-135.
[15]Limon D,Alvarado I,Alamo T,Camacho E F.MPC for tracking of piece-wise constant references for constrained linear systems [J].Automatica,2008,44 (9):2382-2387.
[16]Xi Yugeng,Li Dewei,Lin Shu.Model predictive control status and challenges [J].Acta Automatica Sinica,2013,39 (3):222-236.
[17]Furqan Tahir,Imad M Jaimoukha.Robust feedback model predictive control of constrained uncertain systems [J].Journal of Process Control,2013,23 (2):189-200.
[18]Ferramosca A,Limon D,Alvarado I,Alamo T,Camacho E F.MPC for tracking with optimal closed-loop performance [J].Automatica,2009,45 (8):1975-1978.
[19]Zhu Xiaojing,Pu Dingguo.A restoration-free filter SQP algorithm for equality constrained optimization [J].Applied Mathematics and Computation,2013,219 (11):6016-6029.
[20]Ding Lijuan (丁丽娟).Numerical Calculation Method (数值计算方法) [M].Beijing:Beijing Institute of Technology Press,1997.
[21]Qian Jixin (钱积新),Zhao Jun (赵均),Xu Zuhua (徐祖华).Predictive Control (预测控制) [M].Beijing:Chemical Industry Press,2007.
