雷诺数对低压涡轮附面层转捩影响的数值研究

张银波，郑　伟

（1.中国民航大学航空工程学院发动机系，天津300300；2.天津职业大学机电工程与自动化学院，天津300410）

雷诺数对低压涡轮附面层转捩影响的数值研究

张银波1，郑伟2

（1.中国民航大学航空工程学院发动机系，天津300300；2.天津职业大学机电工程与自动化学院，天津300410）

使用CFX软件对超高负荷低压涡轮叶型吸力面的非定常转捩过程进行数值模拟，并利用试验数据对其结果进行了验证。考察了不同雷诺数（Re=80 000、100 000）对附面层流动发展的影响，并通过附面层流场细节分析，得出了雷诺数对分离、转捩的作用，证实高雷诺数下转捩的发生更靠近上游，使得分离减弱、损失减小。同时，借助频谱分析方法，证明雷诺数不同不会改变Kelvin-Helmholtz和Tollmien-Schlichting不稳定性对转捩的影响。

航空发动机；低压涡轮；分离泡；转捩；叶型损失；雷诺数；频谱分析；数值模拟

1　引言

在大涵道比涡扇发动机中，低压涡轮重量可占到整台发动机重量的20%～30%［1］。而超高负荷低压涡轮的使用，可在减少叶片数量、降低发动机重量、提高推重比的情况下，不降低对风扇的输出功。但该叶型的使用会导致载荷系数增加，从而增大涡轮流道内的逆压梯度，造成涡轮在高空巡航状态低雷诺数工况下，叶片气流极易分离。对于低压涡轮，其叶片展弦比较大，端区的三维损失相比于二维损失在总损失中将占有较大的比例［2］。因此，认识吸力面附面层内气流的运动规律，研究分离泡的形成、发展及上游来流状态对附面层发展的影响，成为超高负荷低压涡轮叶片设计关注的焦点，这也是本文研究的主要内容。

当前，国内外对于如何降低涡轮叶型损失进行了大量研究。1998年，Schulte等通过研究第一次指出，尾迹扫掠对低压涡轮的分离有抑制作用，可用于降低叶型损失［3］。2003年，Ali使用热膜对PAK-B叶型的定常及非定常工况进行了测试，发现尾迹扫掠对吸力面分离泡的起始、再附位置及转捩的起始有较大影响，从而影响叶型损失。Zhang使用PIV对T106C叶型进行了试验研究，通过多张瞬态图片发现非定常状态下尾迹过后的卷起涡，验证了Stieger等在2004年提出的假设［4］。张波对PAK-B叶型开槽，分析了不同攻角对附面层分离、转捩的影响，发现U型槽这种被动控制方式对抑制分离、降低损失非常有效［5］。

上述研究较全面地覆盖了尾迹扫掠及被动控制手段对附面层的影响，但其研究均针对中等或较低载荷系数叶型（Zweifel＜1.2）展开，且此类叶型的失速雷诺数（附面层刚开始分离）通常大于或接近发动机巡航状态工作雷诺数。同时，在定常来流条件下，附面层转捩也是一个非定常过程，如果再结合尾迹扫掠这一非定常过程，分析过程将显得繁琐、杂乱。因此，本文选择超高负荷低压涡轮叶型（Zweifel＜1.4）作为研究对象，重点分析定常来流条件下，吸力面表面分离泡及转捩过程的非定常发展过程。

2　数值计算及结果准确性验证

2.1数值方法

选用CFX商用软件为研究工具，使用ICEM模块进行网格划分，图1为计算域拓扑结构。x方向为叶栅轴向，进口段为0.5倍轴向弦长（Cx），出口段为1.2Cx；y方向为栅距方向，长度为一倍栅距，其两个边界设为周期性边界；z方向为叶片展向，长度为0.2Cx，其上下两个面设为可滑移平面。以上设置在减少计算量的同时，又能保证展向三维涡的形成［6］。

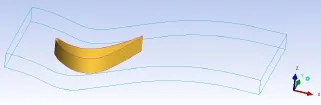
图1　R计算域拓扑结构Fig.1 Themesh topology

叶片周围使用O型拓扑网格，其外为H型拓扑网格。x方向包含300个节点，y方向包含130个节点，z向包含30个节点。叶片表面第一层近壁网格保证y+＜1，Δx+和Δy+在所研究雷诺数范围内处于10～30范围。

定常工况采用RANS方程的CFX-Solver对模型求解，并搭配使用SST湍流模型及gamma-theta转捩模型。非定常工况的求解基于定常工况，采用LES Smagorinsky湍流模型，对流项离散格式为有界中心差分格式，计算的物理时间步长Δt为4.88×10-5s（通过Δt·Vmax/Δxmin≈1关系式得出，其中Vmax为流场内最大速度，Δxmin为计算域内最小网格长度）。

2.2数值方法的验证

图2给出了来流湍流强度FSTI=2.2%、雷诺数Re=80 000时，数值结果与试验结果载荷系数对比。可见，数值模拟对叶型壁面流场的预测较为准确，特别是关于分离转捩研究的速度峰值点（x/SSL=0.425，SSL为吸力面长度）、分离点（x/SSL= 0.500）和再附点（x/SSL=0.600）等几个重要关注点；但对压力恢复点处载荷系数的预估存在一定偏差，这主要是因为SST+gamma-theta模型是根据平板实验数据修正而来，对于大曲率的叶片表面流场计算必然存在一些偏差［7］。图3为同工况下不同壁面位置处速度型的数值与试验数据对比，其中壁面位置选取主要集中在分离之前至转捩完成之后这一重要研究区域。可见，数值模拟可较好地预测分离泡附近的流场，同时能捕捉到试验无法精确测量的近壁区域（y/s＜0.006，s为栅距）。

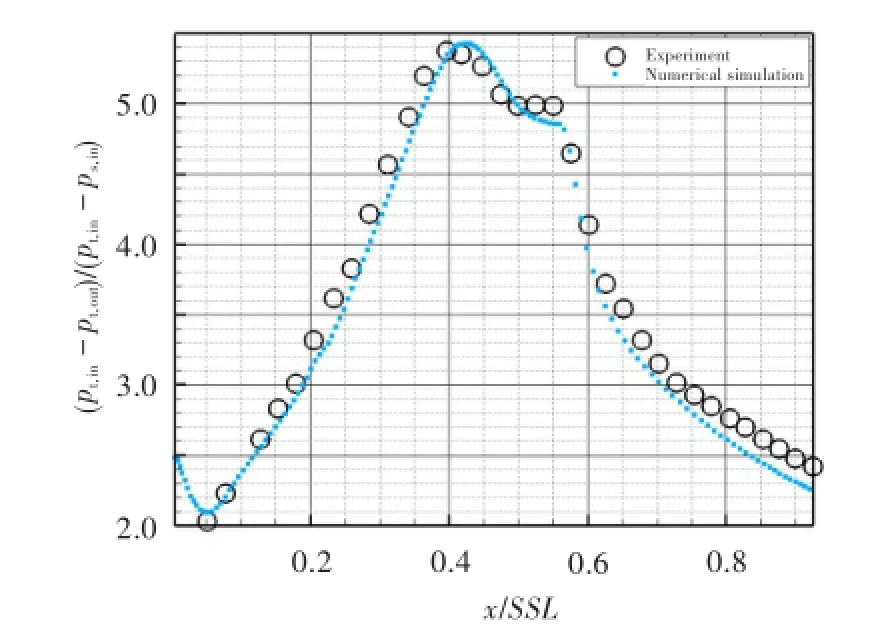
图2　R FSTI=2.2%、Re=80 000时数值结果与试验结果载荷系数对比Fig.2 The loading coefficient comparison of the numerical resultsand experimental data（FSTI=2.2%，Re=80 000）

3　雷诺数对吸力面流动的影响

3.1雷诺数对叶型气动性能的影响

图4为叶型损失随雷诺数的变化曲线。图中，叶型损失使用FSTI=2.2%、Re=80 000时的叶型损失Ymref进行无量纲化，为进口总压，pt，out为出口总压，Uout为出口速度。可见，当Re＞80 000时，叶型损失均处于较低水平，这是由于分离后产生的再附使得分离泡较小，从而使得叶型损失较小；当Re＜80 000时，叶型损失明显增大；当Re=70 000时，吸力面的分离泡完全处于非再附的开始分离状态，损失明显增大。

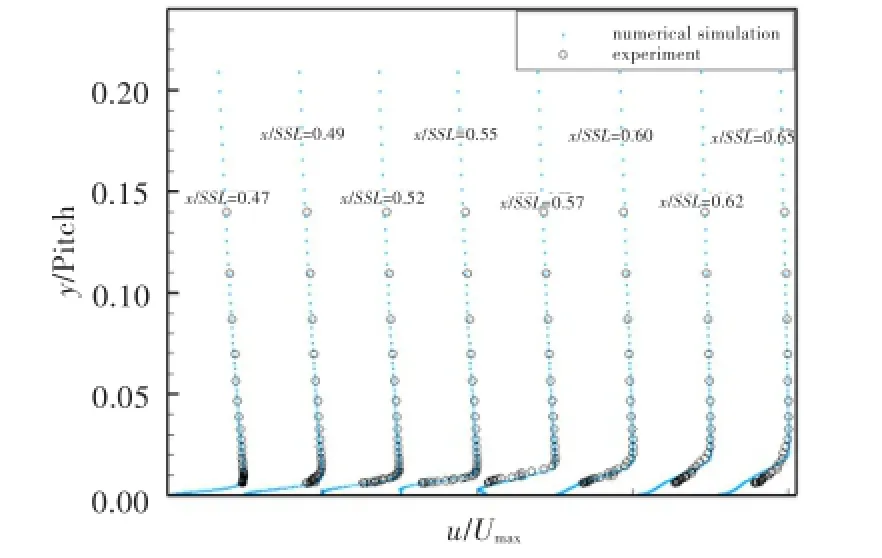
图3　R FSTI=2.2%、Re=80 000时数值结果与试验结果速度型对比Fig.3 The velocity shape comparison of the numerical resultsand experimental data（FSTI=2.2%，Re=80 000）

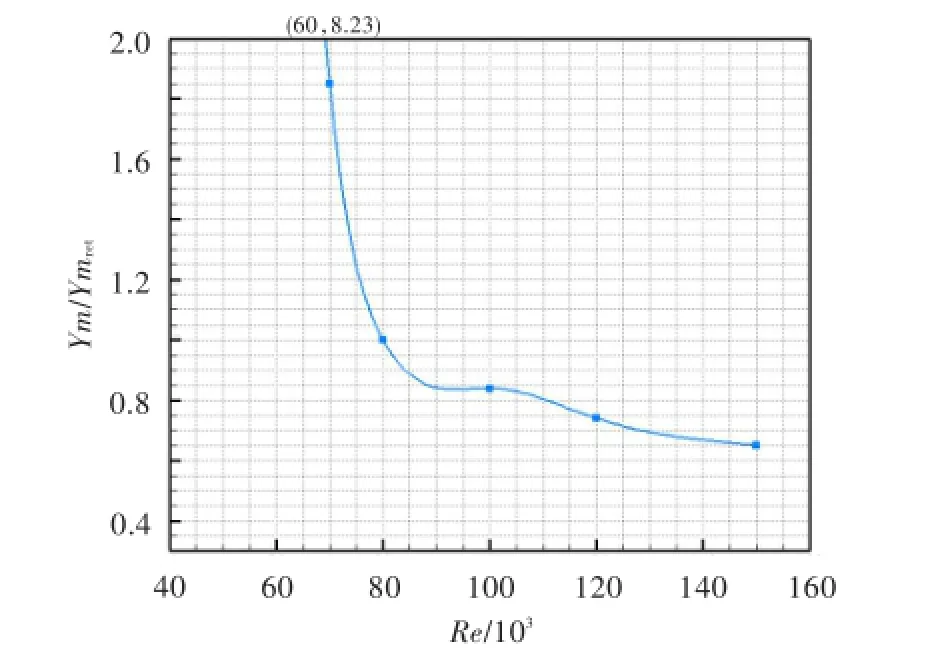
图4　R FSTI=2.2%时叶型损失计算结果Fig.4 The calcu lated profile loss（FSTI=2.2%）

根据Howell等［8］的研究，叶型损失中吸力面损失占到总损失的60%，而损失绝大部分又与分离泡有关，因此非常有必要研究吸力面附面层内气流的运动规律，分离泡的形成、发展、抑制及消除。

图5为FSTI=2.2%，Re=70 000、80 000、100 000时吸力面的载荷系数分布图。可见，叶片表面无分离泡时，载荷曲线的峰值点至尾缘点间这一逆压梯度区无平台突起；有分离泡时，由于分离区内涡系复杂，流动将不再呈现固有趋势，而出现平台突起——突起的起始点对应着分离点，突起的尖点对应着压力恢复点，突起的结束点对应着分离的结束。对比Re=80 000和100 000下的载荷曲线可看出，雷诺数增大时，速度峰值点、分离点位置基本不变，速度峰值点上游加速区内的载荷曲线基本重合，而压力恢复点、再附点位置略向下游移动。另外，从图中还可看出，高雷诺数时分离泡较小。根据Houtermans等［9］的研究结果，图中的分离泡显然都属于短分离泡。短分离泡的位移效应较弱，仅局部影响壁面压力分布，其导致的流动损失对叶型损失贡献甚微。

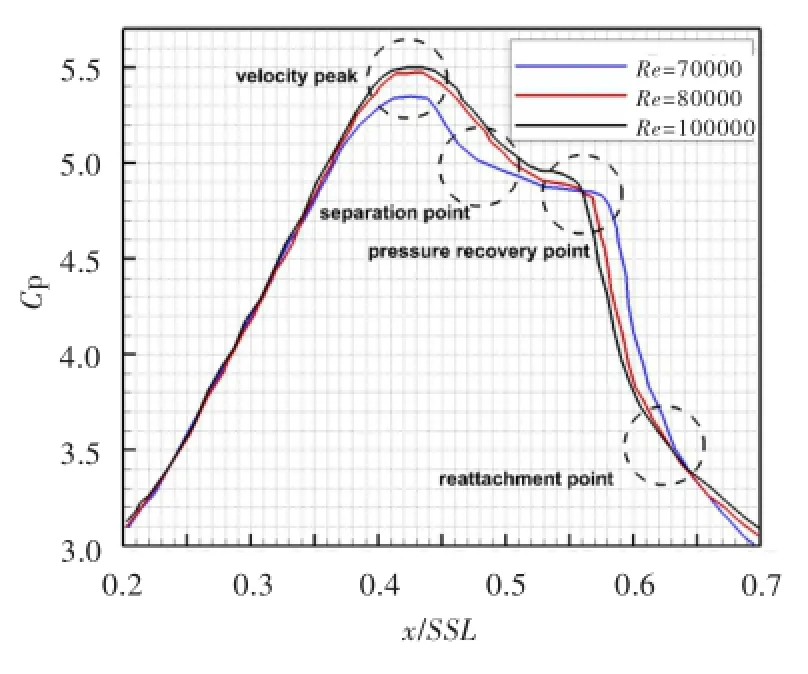
图5　FSTI=2.2%，Re=70 000、80 000、100 000时载荷系数计算时均结果Fig.5 The calculated time-mean loading coefficient （FSTI=2.2%，Re=70 000，80 000，100 000）

图6R为两种雷诺数工况下的速度云图对比。可见，图中三种流线均随雷诺数的增大而下降；两种工况分离泡的起始点都是x/SSL=0.50，但分离的终止分别发生在x/SSL=0.60和x/SSL=0.58两个位置，说明高雷诺数工况下分离泡的长度较短，这与图5中载荷系数预测结果一致。

3.2雷诺数对转捩的影响

通过前文分析发现，高雷诺数下分离泡会减小，损失会下降，附面层流动出现转捩是损失减小的根本原因。转捩过程中，间歇因子是一重要特征指标［10］。

图7、图8分别示出了两种工况下的间歇因子和湍流度云图，给出了各自工况的最大扰动速度线，该曲线为全流场中速度脉动最大曲线，同时还是主流与附面层能量交换最为活跃的区域。图中所反映的两种工况均为分离流动转捩，转捩过程主要由两种不稳定机制导致：一种是Kelvin-Helmholtz（K-H）不稳定性，另一种是Tollmien-Schlichting（T-S）不稳定性。K-H无粘不稳定性通常作用于远壁区域，而T-S粘性不稳定性通常作用于近壁区域。两部分区域的交汇分叉处转捩通常最为活跃，该处的间歇因子梯度最大，同时该处又与最大扰动速度线相重合，如图7所示，找到最大扰动速度线也就找到了转捩线。观察图8可以发现，最大扰动速度线也是湍流度增长的最大梯度线。相比之下，低雷诺数下转捩区域更宽广，湍流核心区域更大。

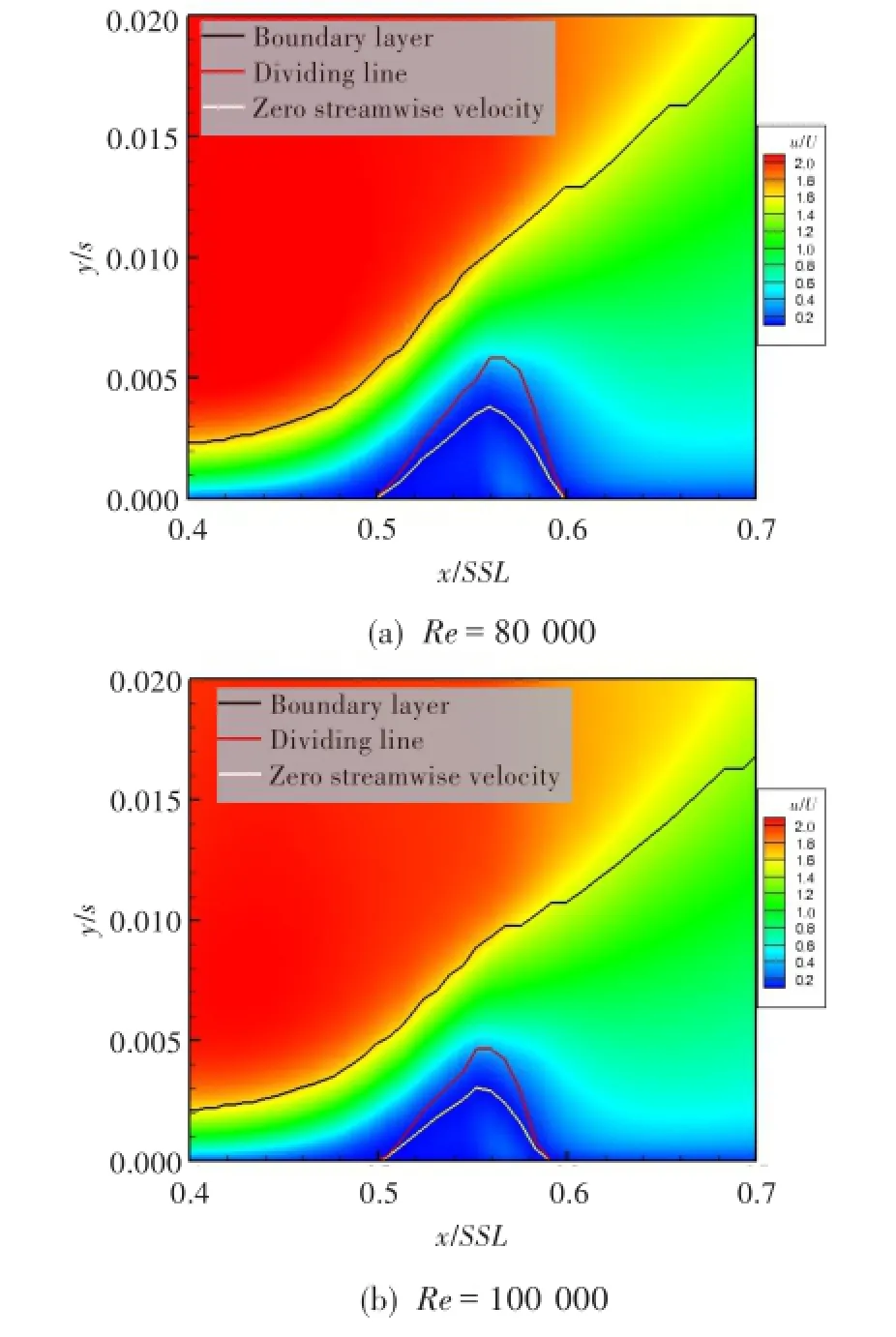
图6　R FSTI=2.2%、Re=80 000和100 000时的时均速度云图Fig.6 The time-mean velocity contours （FSTI=2.2%，Re=80 000 and 100 000）

为了对比两种工况转捩情况，用图7（b）减去图7（a）可得到图9，即间歇因子差。可见，正值区Region1代表高雷诺数工况的K-H转捩，较低雷诺数工况更靠近上游；正值区Region2代表高雷诺数工况的T-S转捩，较低雷诺数工况更靠近壁面。Region1下游的负值区也从另一个侧面说明，低雷诺数工况的K-H转捩晚于高雷诺数工况。另外，高雷诺数工况下的最大扰动速度曲线，较低雷诺数工况更靠近壁面。

综上分析可以看出，高雷诺数工况将使得附面层的K-H无粘不稳定性转捩更靠近上游，使得T-S粘性转捩更贴近壁面，同时会使转捩区及湍流区变小，这一趋势与分离泡及附面层的变化趋势一致。

图10中给出了两种工况下位移厚度、动量厚度及形状因子H12曲线，其中左侧纵坐标适用于位移厚度和动量厚度。位移厚度和动量厚度由当地速度与主流速度积分而来；形状因子为两者之比，是表示附面层内速度型分布的参数，其值越小表示速度剖面越饱满，剖面内流体动能越高；反之则呈凹状分布，此时剖面内流体出现回流［11］。对于后加载涡轮叶片，H12＞3.5通常会发生附面层分离，H12＜3.5后附面层会再附。图中横向黑色虚线表示H12=3.5的分界线。可见，两种工况下H12曲线同时到达3.5的分界线，但高雷诺数工况较早掉回3.5的分界线以下。这说明高雷诺数的分离点与低雷诺数的一致，但分离结束点处于低雷诺数的上游，与前文对分离泡长度的预测一致。

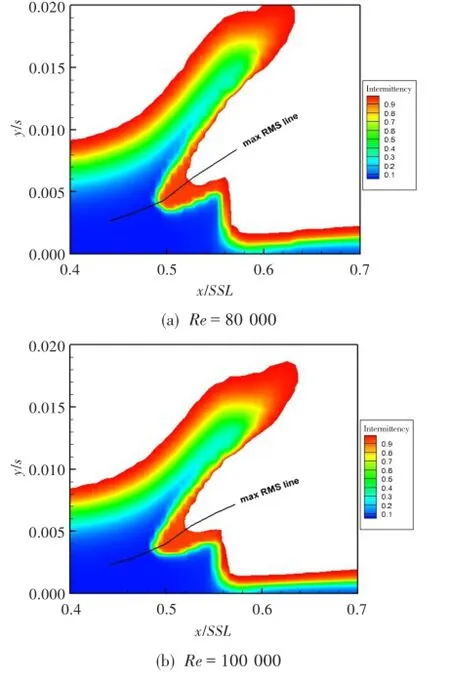
图7　R FSTI=2.2%、Re=80 000和100 000时的间歇因子云图Fig.7 The interm ittent factor contours （FSTI=2.2%，Re=80 000 and 100 000）

位移厚度通常存在两个拐点，第一个拐点对应分离泡最大厚度，第二个拐点对应转捩的结束，其位置在图中由纵向虚线标出。可见，高雷诺数下两处拐点均较低雷诺数靠近上游，由此可推断高雷诺数下分离泡最大厚度较低，且转捩结束较早，使得转捩提前发生，最终使分离减小、损失降低。因此，提前触发转捩将对低雷诺数下低压涡轮叶型损失起到一定的抑制作用。通过两种方法可触发转捩前移，一种是提高来流雷诺数，另一种是提高FSTI，本文基于第一种方法。图11为不同雷诺数下最大速度扰动沿流向的发展曲线，揭示了提高来流雷诺数如何提前触发转捩。在x/SSL=0.53之前，两工况的扰动能量相同。继续向下游发展，高雷诺数工况的扰动能量开始增加，在x/SSL=0.57扰动能量到达峰值后趋缓；而低雷诺数工况的扰动能量在x/SSL=0.60时才开始增加，并在x/SSL=0.66时达到峰值后趋缓，两者峰值点的差异造成转捩位置不同。低雷诺数工况下对应的最大扰动度比高雷诺数工况的高，造成两种工况的转捩范围及转捩后的湍流强度出现差异。

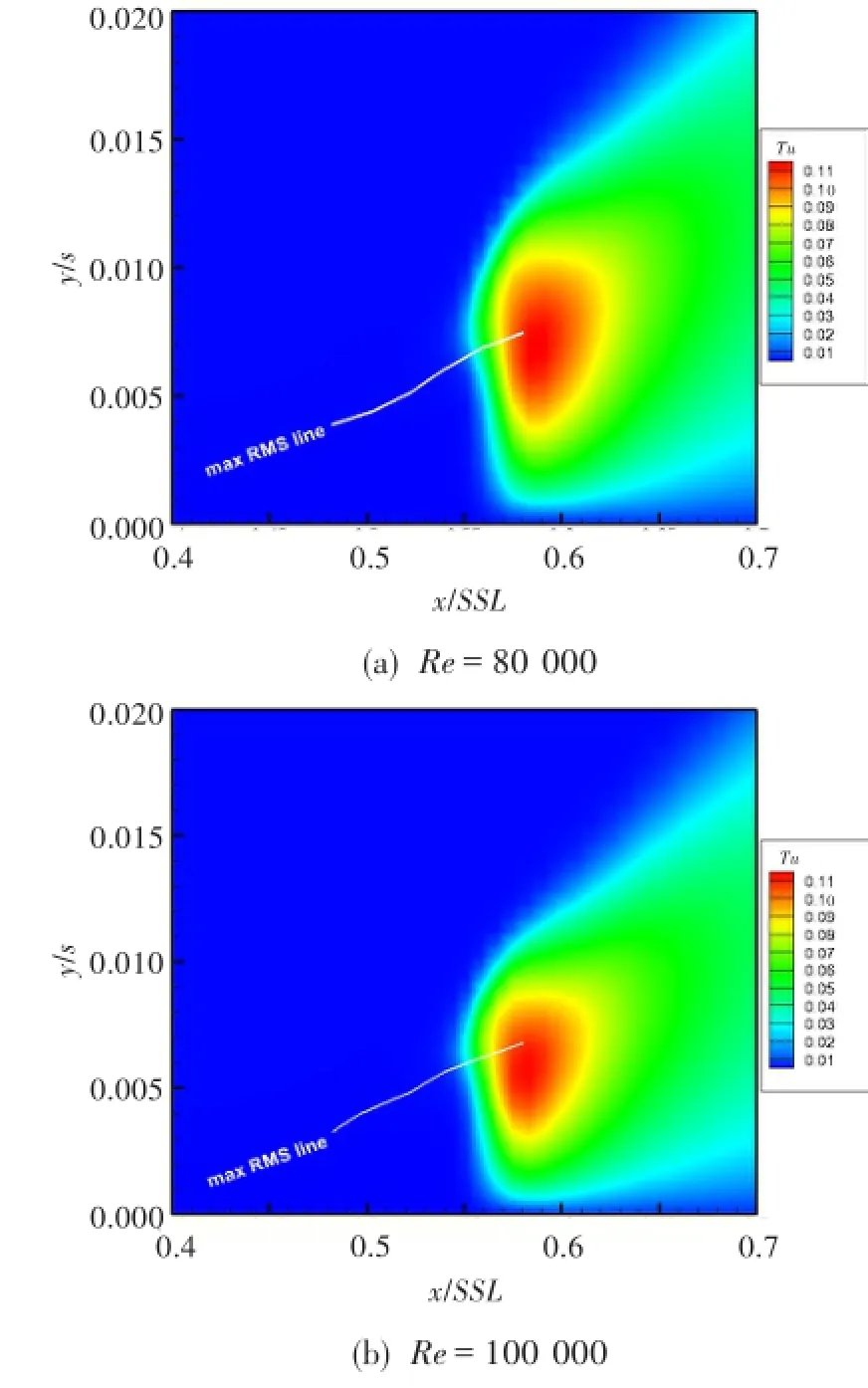
图8　R FSTI=2.2%、Re=80 000和100 000时的时均湍流度云图Fig.8 The time-mean turbulence intensity contours （FSTI=2.2%，Re=80 000 and 100 000）

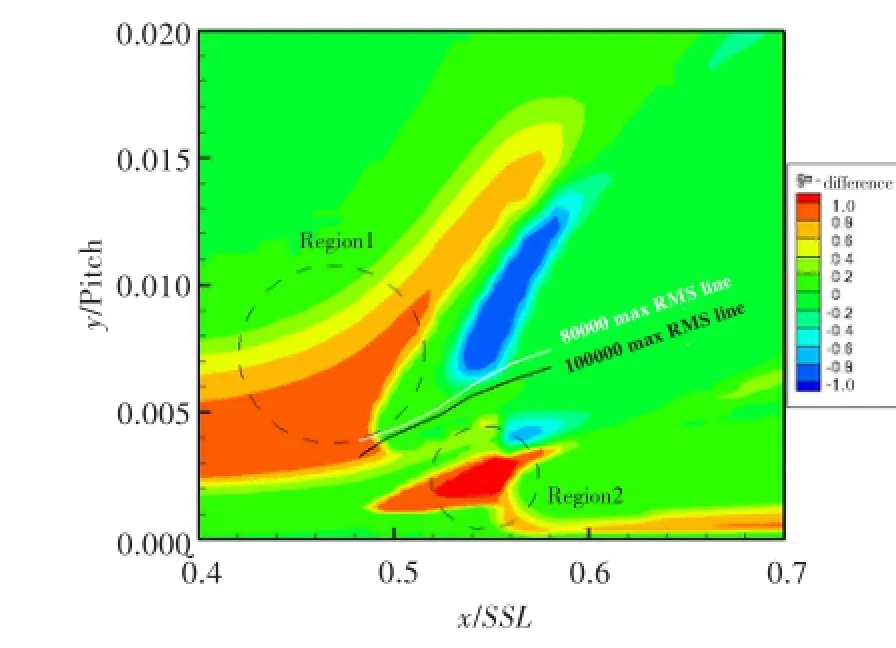
图9　R FSTI=2.2%、Re=80 000和100 000间歇因子之差Fig.9 The interm ittency difference between Re=80 000 and 100 000（FSTI=2.2%）

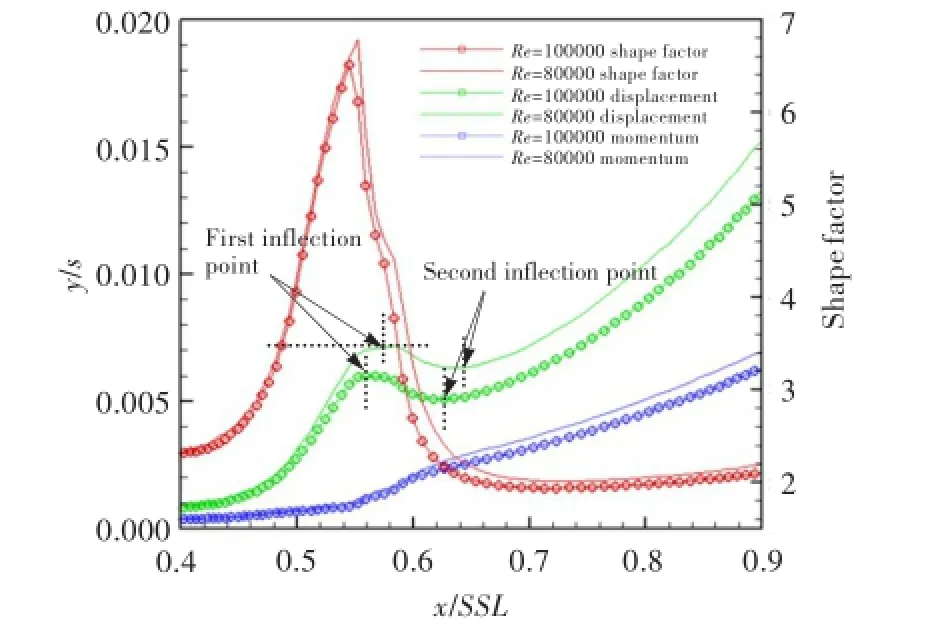
图10　R FSTI=2.2%、Re=80 000和100 000时的位移厚度、动量厚度、形状因子曲线Fig.10 The displacement thickness，momentum thickness and shape factor at Re=80 000 and 100 000（FSTI=2.2%）

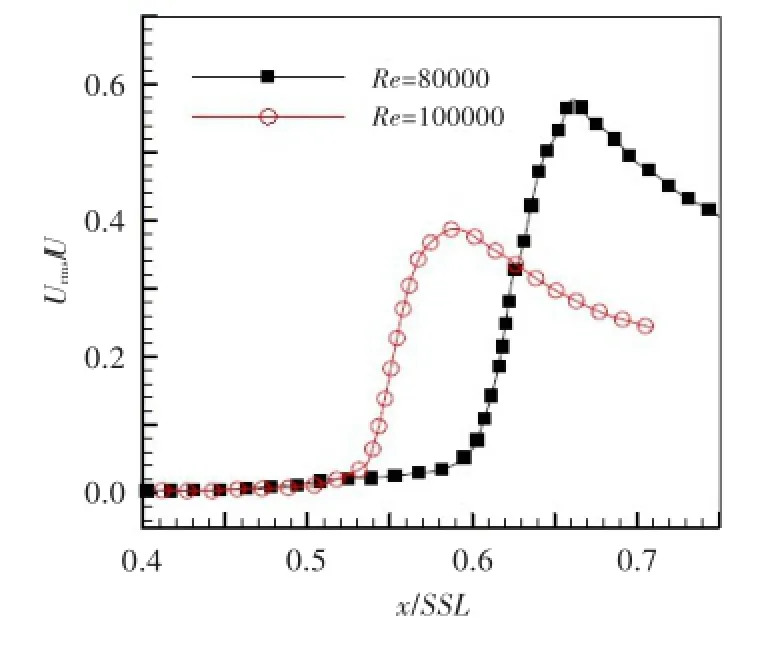
图11　R FSTI=2.2%、Re=80 000和100 000时的速度扰动发展曲线Fig.11 The velocity RMS at Re=80 000 and 100 000 （FSTI=2.2%）

3.3雷诺数对频谱的影响

在自然转捩及分离转捩中通常会产生T-S波，并沿主流方向传播。此不稳定性常在转捩初期当流动还为层流流动时就会出现，Walker［12］根据试验给出的T-S扰动频率fTS为：

对于K-H扰动不稳定性，Volino［13］同样给出了其fKH：

式中：K为近似于1的常数，δs为当地附面层厚度。

本文选取x/SSL=0.60，y/s=0.008、0.020、0.080三个位置（分别以点1、点2和点3代替）作为监测点，对比较的两种工况进行频谱分析。频谱分析采样频率为大涡模拟物理时间步长的倒数f=20 480Hz，采样点数为20 480，使用hanning窗对速度脉动U′数据进行低通滤波，滤波截止频率为6 000Hz，采用20 480点的快速傅立叶变换，最大频率识别范围10 240Hz。

图12给出了低雷诺数和高雷诺数工况三个监测点的频谱图。可见：①高雷诺数工况三个监测点的脉动能量比低雷诺数工况的低，这与图11中高雷诺数工况速度扰动峰值比低雷诺数工况低一致；②高雷诺数工况三个监测点首次出现T-S波的频率比低雷诺数工况的高，但K-H波的频率并未比低雷诺数工况的高，这与经验公式的预测相违背，其原因可能是附面层厚度估计出现偏差；③两种工况下T-S波和K-H波区域，均有与扰动基频成倍频关系的谐波出现。

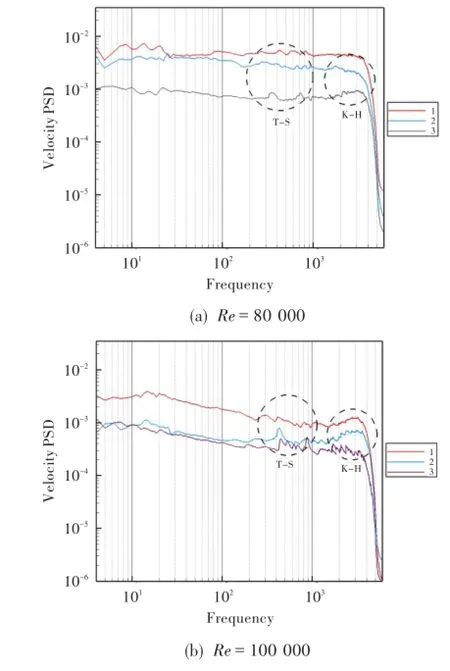
图12　R FSTI=2.2%、x/SSL=0.055时不同法向位置的频谱图Fig.12 The spectrum atdifferentnormal location （FSTI=2.2%，x/SSL=0.055）

表1示出了两种工况下三个检测点扰动基频计算值与预测值的对比。可见，无论是fTS还是fKH，其理论值与计算值均处于同一量级，且误差均小于20%，但高雷诺数工况fKH的理论值与计算值间的偏差还是较大，原因在于对边界层的预估存在偏差。

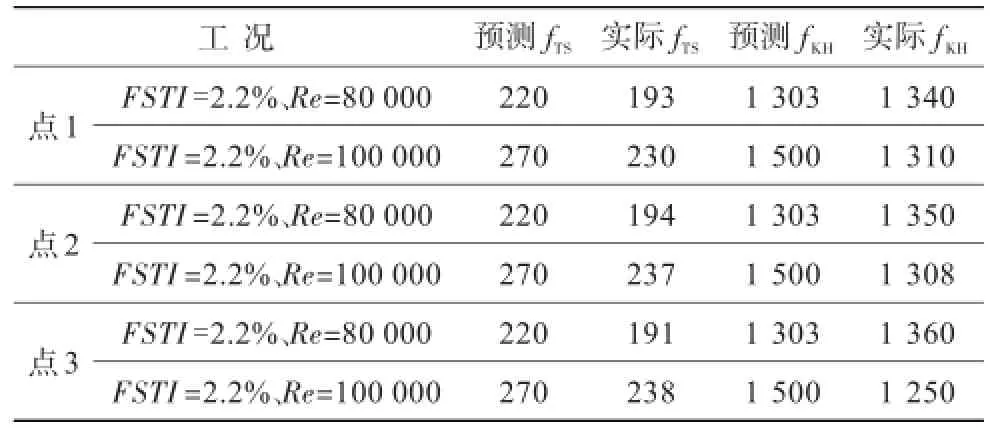
表1　R不同工况下计算与预测频率对比Table 1 Comparison between calculation frequency and prediction frequency under various conditions

4　结论

本文使用大涡模拟计算模型，研究了不同雷诺数对超高负荷低压涡轮吸力面附面层分离、转捩的影响，得出以下结论：

（1）与试验数据的对比表明，本文使用的大涡模拟模型可较好地预测附面层的分离、转捩，以及其他流场细节。

（2）随着雷诺数的增大，附面层分离点没有发生变化，但再附点与转捩点将向上游移动，使得主流能量较早进入低能附面层，减小了分离泡尺寸，降低了叶型损失。

（3）通过不同工况下的间歇因子、湍流度、形状因子、最大速度扰动，反向证明了结论（2）；同时，计算的T-S和K-H频率与经验数据基本一致，说明T-S和K-H同时影响不同雷诺数下的附面层转捩。

［1］Hodson H P，Howell R J.The role of transition in high-lift low-pressure turbines for aero-engines［J］.Progress in Aerospace Sciences，2005，41：419—454.

［2］Curtis EM，Hodson H P，Banieghbal M R，et al.Development of blade profiles for low-pressure turbine applications［R］.ASME 96-GT-358，1996.

［3］Schulte V，Hodson H P.Unsteadywake-induced boundary

layertransitioninhighliftLPturbines［J］.ASMEJournal ofTurbomachinery，1998，120：28—35.

［4］ZhangXF，HodsonH.EffectsofReynoldsnumberand freestreamturbulenceintensityontheunsteadyboundary layerdevelopmentonanultra-high-liftlowpressureturbineairfoil［J］.JournalofTurbomachinery，2010，132（1）：1—10.

［5］张波，李伟，杜强，等.U型槽对高负荷涡轮叶片攻角特性影响［J］.航空动力学报，2012，27（7）：1503—1510.

［6］MittalR，VenkatasubramanianS，NajjarPM.Large-eddy simulationofflowthroughalow-pressureturbinecascade ［R］.AIAA2001-2560，2001.

［7］MenterFR.Two-equationeddy-viscosityturbulence modelsforengineeringapplications［J］.AIAAJournal，1994，32（8）：1598—1605.

［8］HowellRJ，RameshON，HodsonHP，etal.Highliftand aftloadedprofilesforlowpressureturbines［R］.ASME 2000-GT-201，2000.

［9］HoutermansR，CotonT，ArtsT.AerodynamicperformanceofaveryhighliftLPturbinebladewithemphasis onseparationprediction［R］.ASMEGT2003-38802，2003. ［10］MahallatiA.Aerodynamicsofalow-pressureturbineairfoilundersteadyandperiodicunsteadyconditions［D］. Canada：CarletonUniversity，2003.

［11］CoullJD，ThomasRL，HodsonHP.Velocitydistributionsforlowpressureturbines［R］.ASMEGT 2008-50589，2008.

［12］WalkerGJ.Transitionalflowonaxialturbomachineblading［R］.AIAA87-0010，1987.

［13］VolinoRJ.Separatedflowtransitionundersimulated low-pressureturbineairfoilconditions:Part1-meanflow andturbulencestatistics［R］.ASMEGT2002-30236，2002.

Num erical investigation for the effect of Reynolds num ber on low pressu re turbine transition

ZHANG Yin-bo1，ZHENGW ei2
（1.College of Aeroengine Engineering，Civil Aviation University of China，Tianjin 300300，China；2. Tianjin Vocational Institute，SchoolofMechatronical Engineering and Automation，Tianjin 300410，China）

The unsteady transition process of a low pressure turbinewith ultra-high loadingwas investigated by using CFX software.The numerical simulation resultswere also validated with the experimental data. The effects of different Reynolds number（Re=80 000、Re=100 000）on the boundary layer development were researched.Through the flow field analysis，itwas found that the higher Rewould lead an earlier transition，weaken the separation bubble and reduce the profile loss.The spectrum analyzing method was also used，and the results proved that the Kelvin-Helmholtz instability and Tollmien-Schlichting instability were not influenced by the Re in the transition process.

aero-engine；low pressure turbine；separation bubble；transition；profile loss；Reynoldsnumber；spectrum analyzingmethod；numerical simulation

张银波（1979-），男，河南新郑人，讲师，主要从事航空发动机性能计算。

V231.3

A

1672-2620（2015）02-0014-06

2014-07-21；修回日期：2014-12-26

中国民航大学科研启动资金（2014QD22X）；中国民航大学科研启动资金（2014QD21X）