基于PID控制的磁轴承转子动力学分析

雷新亮，卿　华

（中国燃气涡轮研究院，成都610500）

基于PID控制的磁轴承转子动力学分析

雷新亮，卿华

（中国燃气涡轮研究院，成都610500）

磁轴承转子动力学特性是磁轴承与转子动力学综合作用的结果，其好坏不仅决定稳定悬浮能否实现，而且还直接影响其动态性能和转子的回转精度。对基于PID控制的主动径向磁轴承的刚度和阻尼特性进行了深入研究，在此基础上，针对五自由度的多电模拟发动机转子进行临界转速、稳定性分析，得到各阶临界转速及稳定与否的判定方法，并分析了轴承主导型临界转速和转子主导型临界转速的不同特性。研究结果能为多电发动机整机减振设计提供技术支持。

多电发动机；主动磁轴承；PID控制；模拟转子；转子动力学；临界转速；稳定性

1　引言

主动磁轴承（AMB）作为一种新的支承形式，具有非接触、无摩擦、无磨损、无振动、无噪声、高可靠性、长寿命、不需润滑和密封等一系列优良品质，从根本上改变了传统的支承形式，在航空航天、能源交通、超高速精密加工等领域具有广阔的应用前景。

为深入研究主动磁轴承转子临界转速特性，使转子无障碍、平稳地通过轴承-转子系统的临界转速，就必须通过深入研究磁轴承的结构特点、机电耦合特性及控制规律，得到主动磁轴承的刚度阻尼特性规律，从而进一步研究磁轴承-转子的动力学问题。而弄清磁轴承-转子系统动力学，是实现主动磁轴承转子能够稳定、安全运转的保证，是实现磁轴承在航空发动机上应用的关键技术之一。

早在1980年，Haberman等［1］就对磁轴承的刚度特性作了研究，并提出了浴盆形复刚度曲线。此后，多数研究者均以此为基础分析磁轴承系统的支承特性。Humphris等［2］用磁轴承系统的传递函数，推导出了磁轴承的等效刚度和等效阻尼计算公式。Baloh等［3］采用最小均方误差自适应估计方法，测试了磁轴承的电流刚度系数和位移刚度系数。Kim等［4］提出基于自适应滤波器参数收敛的方法，实现了电流刚度系数和位移刚度系数的自适应识别功能。Jeon等［5］以柔性转子模型为分析对象，提出了用激励测试获得模型参数和刚度特性的方法。Lim等［6］采用激励的方法，识别了PID控制策略下的磁轴承支承特性参数。国内对磁轴承支承特性也做了大量探索性研究。汪希平［7］对磁轴承的等效刚度和等效阻尼的计算表达式进行了理论推导，并用实验方法测试了磁轴承的复刚度特性［8］，验证了Haberman的浴盆曲线理论；赵雷等［9］分析了控制环节各参数对磁轴承刚度特性的影响；胡业发等［10］研究了考虑交叉刚度和交叉阻尼的磁轴承的支承特性；吴华春等［11］理论分析了滤波、滞后、衰减等因素对磁轴承刚度的影响；刘小静等［12］通过推导非线性刚度公式，分析了控制器参数、位移变化速度对刚度的影响；肖凯等［13］理论研究了基于PD控制的磁轴承刚度与阻尼。

本文通过深入分析磁轴承的刚度、阻尼特性，结合磁轴承转子系统的控制特性，建立了一种磁轴承转子系统的动力学特性分析方法，阐述了轴承主导型临界转速及转子主导型临界转速的区别，分析了控制参数对磁轴承转子系统稳定性的影响。

2　磁轴承刚度和阻尼特性分析

2.1单自由度磁悬浮系统模型

首先建立磁轴承控制系统的数学模型。图1为一个单自由度差动激磁的磁轴承系统框图，图中转子位置可由位移传感器及其变换电路、调节电路和功放电路组成的控制器精密控制。单自由度磁轴承系统控制框图见图2。

整个控制系统分别由传感器、控制器、功率放大器、滤波等环节组成，其控制电流与转子位移的传递函数可表示为：

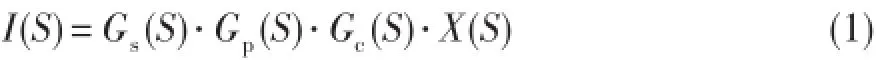
式中：I（S）为系统的控制电流，Gs（S）为传感器的传递函数，Gp（S）为功率放大器的传递函数，Gc（S）为控制器的传递函数，X（S）为转子的位移量，S为拉普拉斯变换算子。可见，磁轴承的刚度和阻尼特性，应与传感器、控制器、功率放大器紧密相关。

2.2位移刚度系数和电流刚度系数

在忽略铁心材料磁阻和转子重力的情况下，磁轴承转子中心的运动方程可表示为：

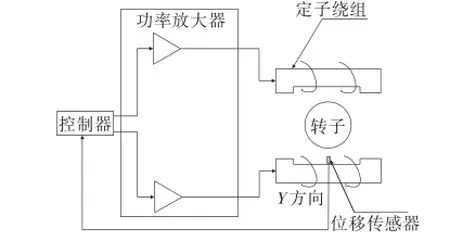
图1　R单自由度磁悬浮系统结构框图Fig.1 The structure of single DOFmagnetic system

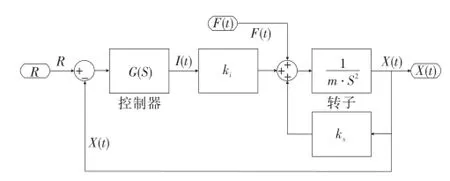
图2　R单自由度磁悬浮系统控制框图Fig.2 The flow diagram of single DOFmagnetic system

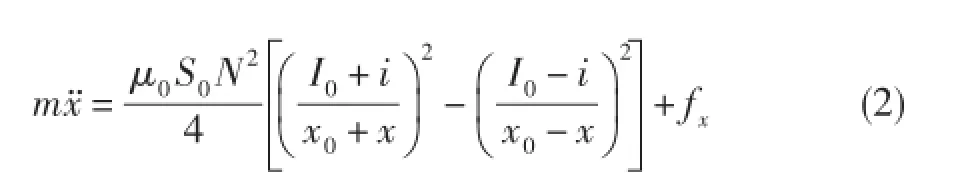
式中：x0为磁轴承转子处于平衡位置的轴承气隙长度，x为磁轴承转子偏离中心的距离，一般x≪x0；I0为偏磁电流分量，i为磁轴承转子因偏心而产生的控制电流，一般i≪I0；μ0为真空磁导率，μ0= 4π×10-7N/A2；S0为磁轴承转子与静子之间气隙截面积；N为电磁线圈匝数。

将式（2）看作磁轴承转子偏心距x的函数，并考虑到磁轴承的实际工作情况（一般情况下x很小，趋近于0），在x=0处采用泰勒公式展开：

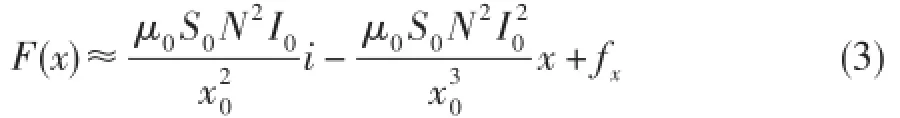
虽然随着x的增加方程（3）的精度下降，尤其是在磁轴承转子与轴承接触、强电流（铁心饱和）及偏磁电流很小等极限状态下，方程（3）绝对不适合；但实践经验及理论都证实，简单的线性化方程（3）在很大范围内都适合。，则式（3）可简

化为：

式中：ki称为磁轴承的电流刚度系数，kx称为磁轴承的位移刚度系数。由于电流刚度系数和位移刚度系数，与磁轴承的气隙截面积、线圈匝数、磁导率、偏磁电流分量、气隙大小有关，而这些参数均为磁轴承的固有参数，因此位移刚度系数和电流刚度系数为磁轴承的固有特性参数，是研究磁轴承的刚度、阻尼特性的基础。

2.3基于PID控制的磁轴承刚度和阻尼特性

采用PID控制器的磁轴承控制方程为：

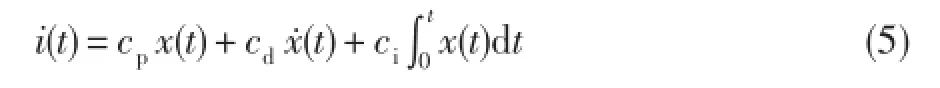
式中：cp，cd，ci分别为PID控制的比例、微分、积分常数，t为时间。其对应的控制器传递函数为：

为便于与普通刚度-阻尼系统比较，需引入广义刚度［14］的概念。为此，对线性化的磁轴承支承力位移和电流函数进行拉普拉斯变换，得：

根据上述定义，若PID控制器的传递函数表达式为式（6），则磁轴承广义刚度表达式为：

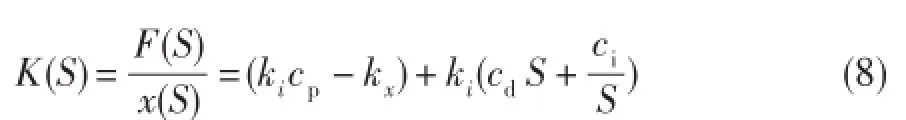
由振动理论可知，普通具有弹簧阻尼特性支承的广义刚度为：

式中：k、c分别为磁轴承刚度和阻尼。

为考察其频域特性，令S=jω，则式（8）可简化为：

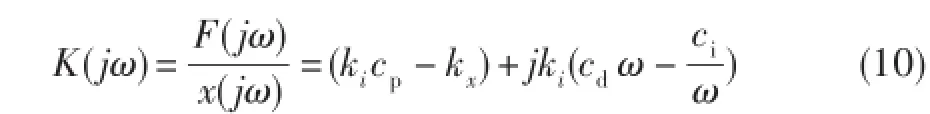
式（9）可简化为：

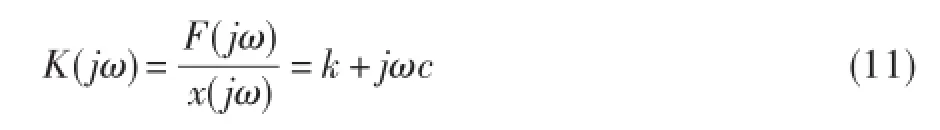
对比式（10）和式（11）可知，要使PID控制的磁轴承等效于一般弹簧阻尼支承，则式（10）、式（11）的实部和虚部必须各自相等，则有：显然，式（12）为磁轴承支承特性（刚度和阻尼）与PID控制参数之间函数关系的显式表达式。

2.4基于磁轴承控制系统的磁轴承刚度和阻尼特性

设某控制器的传递函数为G（S），不失一般性，

将式（12）所得结果合理外推，得到一般控制条件下的磁轴承刚度和阻尼特性公式［15］：

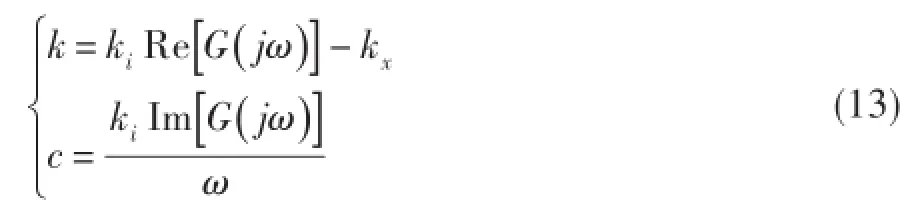
由式（1）可得，整个控制系统的传递函数为：

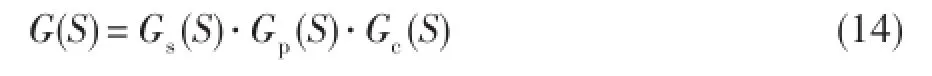
由于磁轴承根据传感器检测的位移信号来调整电磁力的大小及作用方向，进而使转子恢复其理想位置，因此磁轴承系统性能的好坏很大程度上取决于所采用位移传感器的性能。由于磁悬浮转子相对于平衡位置的位置变化量，是由位移传感器检测转换为电压量，再由信号放大器输出，并且为消除传感器电路中的高频噪声，这一环节还带有低通滤波器，所以传感器的传递函数一般为：

式中：As为传感器增益，Ts为传感器滞后时间常数系数。

功率放大器是磁轴承系统的一个重要部件，是控制器控制命令的执行者，它根据控制器的输出在磁轴承定子线圈中产生比例电流信号，以产生所需电磁力，从而使转子运动到控制器所设定的位置，其性能对整个系统有着重要影响。当功率放大器在线性范围内工作时，其等效传递函数为：a

式中：Aa为功率放大器增益，Ta为功率放大器衰减系数。

由式（6）、式（14）～式（16）可知，单自由度磁轴承控制下的传递函数一般形式为：

为考察其频域特性，令S=jω，则式（13）变为：

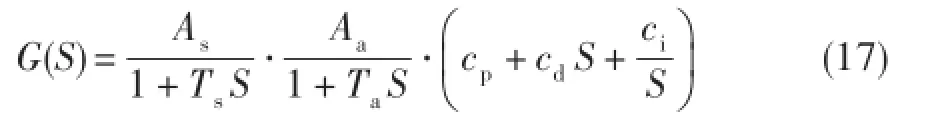
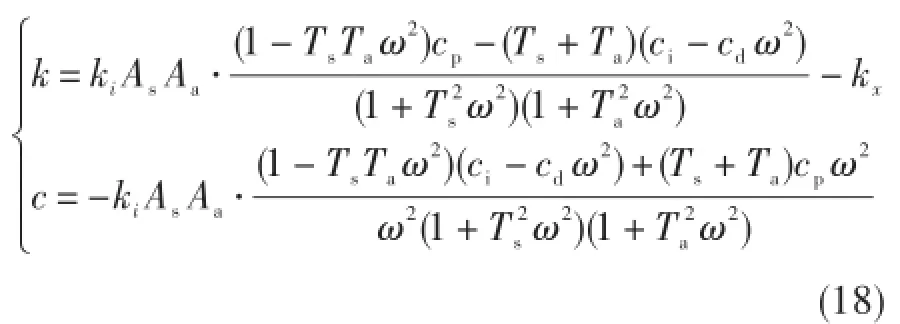
若忽略Ts和Ta的影响，则式（18）可简化为：

式（18）和式（19）即为基于PID控制的磁轴承刚度、阻尼的一般表达式。可见，基于PID控制的磁轴承刚度、阻尼与三方面因素相关：①磁轴承本身的结构、电磁参数，如真空磁导率、转静子气隙截面积、气隙大小、线圈匝数、偏磁电流等；②PID控制器参数（比例系数、积分系数和微分系数）及控制信号频率；③传感器和功率放大器相关参数（传感器、功率放大器增益，传感器滞后时间常数，功率放大器衰减系数）。

实际磁轴承中，磁轴承本身的结构、电磁参数以及传感器和功率放大器相关参数一般确定不变，而PID控制器相关参数可调，因此一般通过调节控制器相关参数来改变磁轴承的刚度、阻尼特性。下面举实例说明。

某实验用径向磁轴承相关参数为：ki=522 N/A，kx=1.74×106N/m，As=8×103V/m，Aa=0.6 A/V，Ts= 5×10-4s，Ta=2×10-5s，cp=3.15，ci=305，cd=0.018。可得到磁轴承支承刚度、阻尼随控制频率的变化，如图3所示。从图中可知：

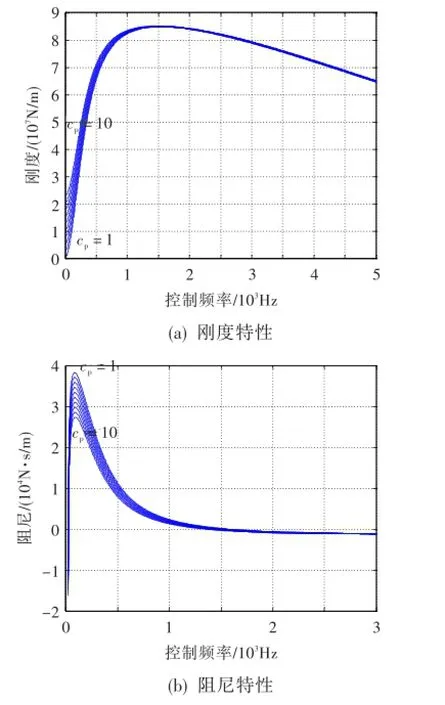
图3　R磁轴承的支承刚度和阻尼特性Fig.3 The stiffnessand damping characteristicsofmagnetic bearing

（1）控制频率在磁轴承共振频率1 600 Hz以下时，支承刚度随控制频率的增大而迅速增大；控制频率超过共振频率后，支承刚度随控制频率的增大而缓慢减小。实际使用中，控制频率应避开磁轴承共振频率。

（2）控制频率在0～20 Hz之间时，支承阻尼小于零；控制频率在20～1 500 Hz之间时，支承阻尼大于零，其中控制频率在85 Hz左右时阻尼值达到最大，而后迅速减小，总体趋势是阻尼先增大后减小；控制频率大于1 500 Hz后，支承阻尼小于零且变化平稳。控制器设计中，必须避开阻尼小于零的控制频率带。

3　磁轴承转子-支承系统动力学分析

以某多电发动机转子为例，根据磁轴承刚度、阻尼特性，采用SAMCEF转子动力学分析软件进行动力学分析。由于关注重点是磁轴承的转子动力特性，故在原多电发动机的基础上，建立了多电发动机模拟转子（图4），其转子动力特性与原多电发动机的基本一致。

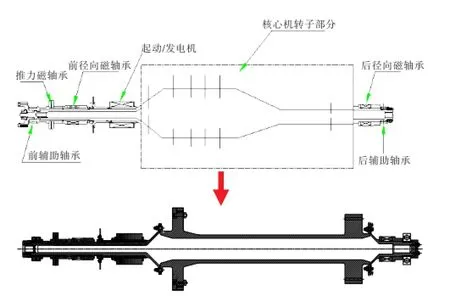
图4　R某型多电发动机结构模型简图Fig.4 The structuremodelofamore-electric engine

从力学模型本质上看，这是一个五自由度磁轴承转子系统。其中前、后径向磁轴承约束转子的四个径向自由度，支撑转子正常运转；推力轴承约束转子的轴向自由度。其中前、后径向磁轴承有8个磁极，8个磁极对转子的作用可简化为8个具有阻尼效果的弹簧，如图5所示。

假定两个磁轴承采用分散式控制，考虑到磁轴承在x、y方向的耦合作用较弱，可将支承简化为各向同性，可得：

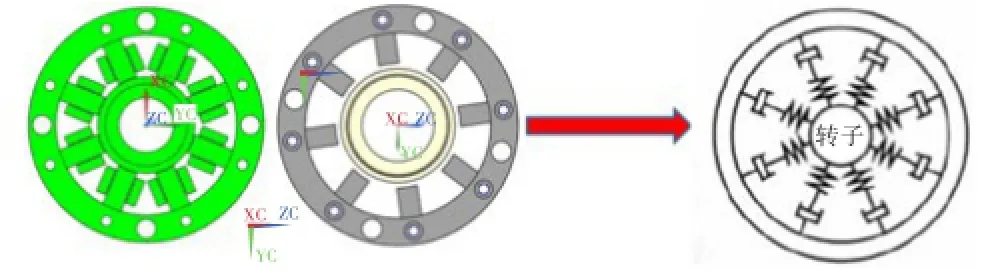
图5　R径向磁轴承简化示意图Fig.5 Idealization diagram of AMB

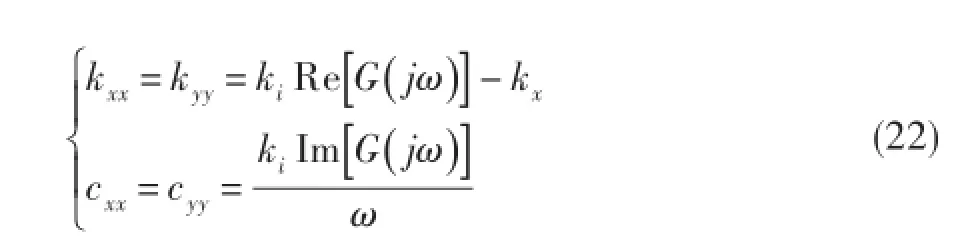
前、后径向磁轴承的kx=6.85×105N/m，ki=61.2 N/A，其他相关参数与2.4节中的一致。则磁轴承刚度、阻尼特性随涡动频率的变化如图6所示。

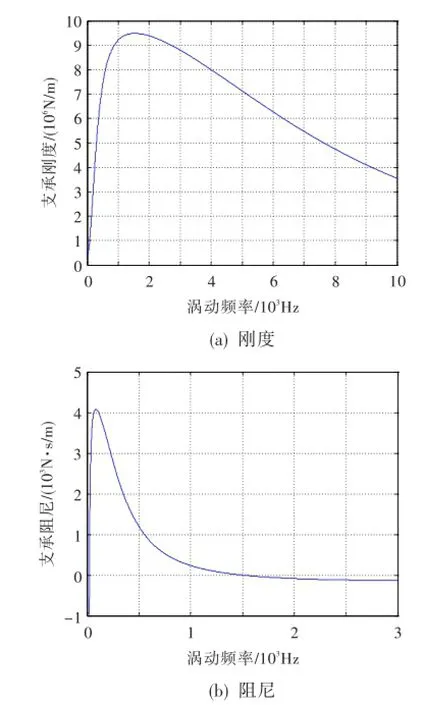
图6　R磁轴承刚度和阻尼与涡动频率的关系Fig.6 Stiffnessand damping vs.whirling frequency

不考虑两个径向磁轴承的阻尼效应，模拟转子临界转速结果如表1所示。图7为模拟转子前六阶临界转速所对应的振型。可见，模拟转子的前两阶临界转速为刚体型临界转速，其中第一阶为平动型，第二阶为俯仰型。由于转子在刚体型临界转速时其应变能主要集中在轴承上，可称为轴承主导型临界转速；第三～第六阶为弯曲型临界转速，应变能主要集中在转子上，可称为转子主导型临界转速。

表1　R不考虑磁轴承阻尼效应的临界转速分析结果Tab le 1 The simulation resu lts at critical speed unconsidering damping effects

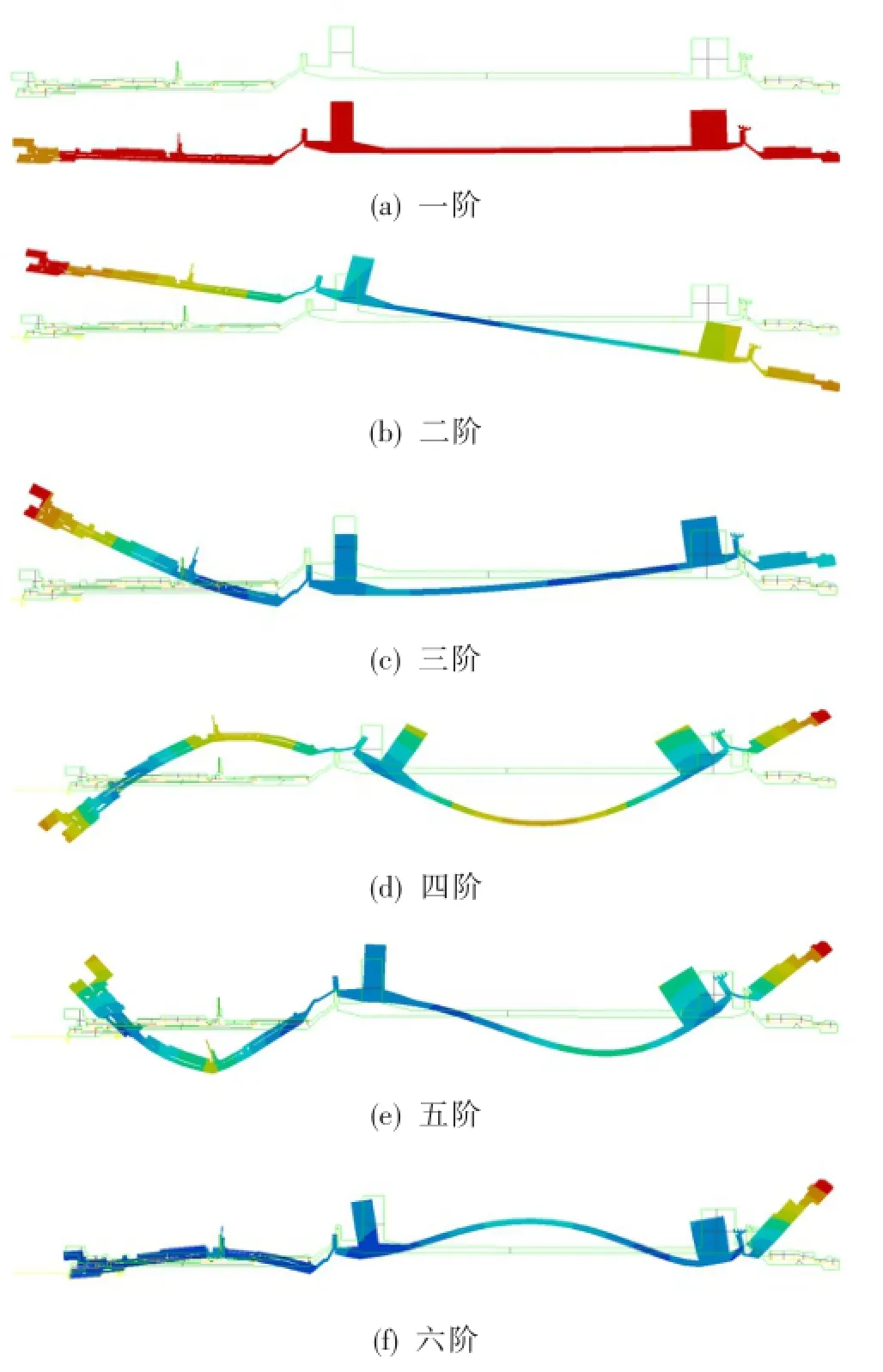
图7　R模拟转子前六阶振型示意图Fig.7 The firstsix vibrationmodesof rotor

考虑磁轴承阻尼效应的情况下，模拟转子临界转速及对数衰减率δ结果如表2所示。振型与图7相似。对比表1和表2可以看出：

（1）考虑磁轴承阻尼效应后，轴承主导型临界转速明显减小，而转子主导型临界转速基本不变。这说明控制器参数变化时，能改变模拟转子轴承主导型临界转速，而不能改变转子主导型临界转速，除非改变转子几何尺寸。

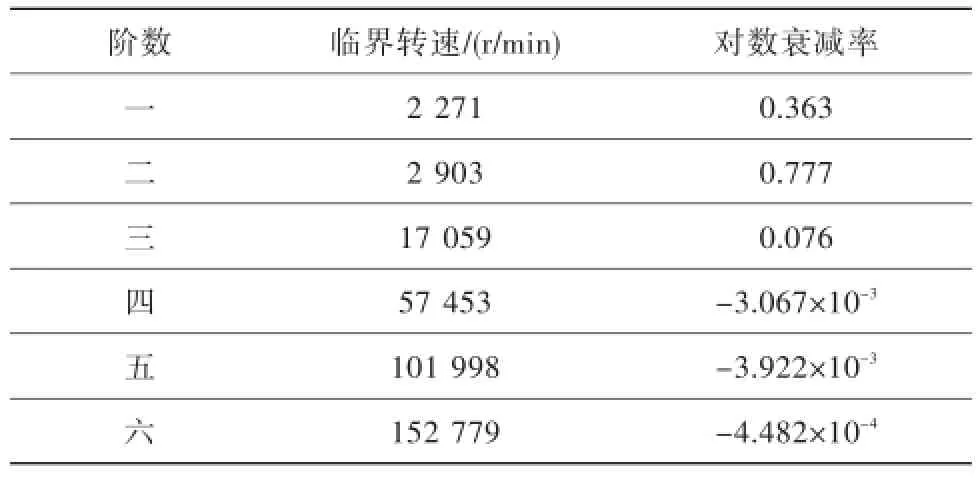
表2　R考虑磁轴承阻尼效应的临界转速仿真结果Tab le 2 The simu lation results at critical speed considering damping effects

（2）考虑磁轴承阻尼效应后，转子前三阶临界转速对应的δ＞0，而后三阶临界转速所对应的δ＜0。这表明在通过后三阶临界转速时转子将失稳，因此必须考虑控制器参数的稳定区域，以避免磁轴承转子在工作转速范围内失稳。

4　结论

（1）磁轴承的刚度和阻尼，除与轴承的固有参数（位移刚度系数、电流刚度系数）直接相关外，还与控制器的传递函数和信号的角频率（即系统信号中可能出现的任何频率成分）有关；分析计算时至少应以转子的涡动频率为依据。

（2）为避免转子失稳，在系统实际运行前，需预知其稳定性及动态特性，避开控制参数选择的非稳定性区域，采取措施避免转子在临界转速附近运行。

（3）磁轴承控制器参数变化时，能改变转子的轴承主导型临界转速，而对转子主导型临界转速影响较小。

（4）本文建立的先由控制系统稳定性理论分析方法获得系统稳定性控制器参数，再基于控制器参数分析转子动力特性，用于指导转子试验，然后由试验结果修正控制器参数的磁轴承转子系统动力特性分析方法，为最终获得系统的临界转速分布和稳定性分析奠定了基础。

［1］Haberman H，Liard G.An activemagnetic bearing system ［J］.Tribology International，1980，13（2）：85—89.

［2］Humphris R，Kelm R，Lew is D，etal.Effectof control algorithms on magnetic journal bearing properties［J］.Journal of Engineering for Gas Turbines and Power，1986，108 （10）：624—632.

［3］Baloh M，Tao G，A llaire P.Adaptive estimation ofmagnetic bearing parameters［C］//.Proceedings of the IEEE International Conference on Control Applications.1999：1193—1198.

［4］Kim S，Lee C.On-line identification of current and position stiffnesses by LMS algorithm inactive magnetic bearing system equipped with force transducers［J］.Mechanical Systemsand Signal Processing，1999，13（5）：681—690.

［5］Jeon S，Ahn H，Han D.Model validation and controller design for vibration suppression of flexible rotor using AMB ［J］.Journal of Mechanical Science and Technology，2002，16（12）：1583—1593.

［6］Lim T，Cheng S.Parameter estimation and statistical analysis on frequency dependent active control forces［J］.Mechanical Systems and Signal Processing，2007，21（21）：2112—2124.

［7］汪希平.磁轴承系统的参数设计与应用研究［D］.西安：西安交通大学，1994.

［8］汪希平.磁轴承系统的刚度阻尼特性分析［J］.应用力学学报，1997，14（3）：95—100.

［9］赵雷，丛华，赵鸿宾.可控磁悬浮轴承刚度与阻尼特性研究［J］.清华大学学报，1999，39（4）：96—99.

［10］胡业发，周祖德，江征风.磁力轴承的基础理论与应用［M］.北京：机械工业出版社，2006.

［11］吴华春，胡业发，江征风.磁力轴承支承特性的影响因素研究［J］.设计与研究，2007，（4）：7—10.

［12］刘小静.主动磁力轴承非线性刚度研究［J］.湖北工业大学学报，2007，22（4）：1—3.

［13］肖凯，张育林，刘昆.基于PD控制的磁轴承刚度与阻尼分析［J］.机床与液压，2007，35（8）：26—35.

［14］吴华春.磁力轴承支承的转子动态特性研究［D］.武汉：武汉理工大学，2005.

［15］胡业发，王晓光，吴华春.磁力轴承支承特性的研究与仿真［J］.武汉理工大学学报，2001，23（4）：96—98.

Analysison m agnetic bearing rotor dynam ics based on PID control

LEIXin-liang，QINGHua
（China Gas Turbine Establishment，Chengdu 610500，China）

The characteristics ofmagnetic bearing rotor dynamics are the interaction results ofmagnetic suspension characteristics and rotor dynamics.Its design level notonly determines the achievementofmagnetic suspension，butalso influences the dynamic characteristics and the precision of the rotor.The stiffness and damping characteristics of radical activemagnetic bearing（AMB）based on PID controlwas investigated.The critic speed and stability of a five DOFsmore-electrical enginewas analyzed.Based on the analyzing results，the critical speed and stability criterion of each degreewere obtained.At last，the different characteristicsof bearing-dominated critical speed and rotor-dominated critical speed were researched.The researching resultswilloffer technicalsupports for the damping design ofmore-electricalengine.

more-electric engine；activemagnetic bearing；PID control；simulated rotor；rotor dynamics；critical speed；stability

雷新亮（1982-），男，湖南临武人，工程师，硕士，主要从事航空发动机强度设计工作。

V231.96

A

1672-2620（2015）02-0020-06

2014-11-27；修回日期：2015-04-10