基于 Tikhonov正则化方法的移动荷载识别实验研究

陈春苗，高　婧

（厦门大学土木工程系 ，福建厦门361005）

基于 Tikhonov正则化方法的移动荷载识别实验研究

陈春苗，高婧

（厦门大学土木工程系 ，福建厦门361005）

摘要：根据正交异性板理论和模态叠加法，推导了移动荷载作用下简支板桥的荷载识别方程。为了解决识别方程病态问题，考虑Tikhonov正则化方法，选择最优正则参数值，从而得到方程的正则化解。为了验证Tikhonov正则化方法的有效性，进行了简支板桥的移动荷载识别模型实验，通过实验确定不同速度车辆经过板桥时的应变响应历程，并将所测得数据代入识别方程求得车辆荷载信息。实验和计算结果对比表明 ，通过引进Tikhonov正则化方法可以获得识别方程的稳定解，提高识别精度，识别结果与实际小车重量吻合较好。

关键词：荷载识别；简支板桥；Tikhonov正则化方法

移动荷载识别是在不中断交通的情况下通过桥梁动态响应来识别桥上的移动荷载，从而获得车辆轴重、轴距、车速等信息，它不仅可以确定移动荷载的大小、密度和种类，而且对桥梁健康监测与超载的治理等都具有重要的意义［1］。通过实测应变与理论计算应变相等而建立的识别方程往往存在严重的病态性，即使测量的数据中存在较小的噪声 ，也可能引起识别荷载较大的偏离［2］。为了获得稳定的荷载识别结果，一般引入正则化方法。

正则化方法分为直接正则化方法与迭代正则化方法［3］。直接正则化方法主要有截断奇异值法与Tikhonov正则化方法，而迭代正则化方法有Jacobi迭代法、Gauss-Seidel迭代法和共轭梯度法等。迭代正则化用于处理各种无限维或者有限维的适定问题［4］，截断奇异值法的奇异值个数很难确定，而Tikhonov正则化方法通过选取不同的正则参数降低方程的病态程度得到稳定解，其基本原理就是通过对病态方程施加约束，改变方程中矩阵的条件数，从而减轻方程的病态程度［5-6］。Zhu通过应变和加速度对简支梁板桥的移动荷载进行识别，采用Tikhonov正则化方法对识别结果进行了平滑度处理，得出Tikhonov正则化方法能降低识别误差并且对应变荷载识别的改善效果更为显著［7］。Buro Happold在Vransko大桥的荷载识别实验中测得了一辆三轴车经过桥梁时应变响应历程，通过有限元计算获取了应变影响线，采用Tikhonov正则化方法识别出桥面比较粗糙的情况下的车辆轴重，并且指出的识别结果较最小二乘法的识别结果误差更小［8］。李忠献在简支梁和连续梁的荷载识别参数分析中，运用Tikhonov正则化方法降低了噪声敏感性，改善识别精度。并且得到正则参数随着噪音水平增大而增大。同等噪音水平下，简支梁的识别效果好于连续梁［9］。

为了验证Tikhonov正则化方法在简支板桥荷载识别方程求解中的有效性，本文主要通过简支板桥移动荷载识别的理论获得应变影响线，通过模型实验获得实测数据 ，并考虑Tikhonov正则化方法求解识别方程。

1　移动荷载识别的理论基础及Tikhonov正则化

图1为各向同性简支板桥模型 ，x=0和x=a为简支边，y=0和 y=b为自由边，有双向多车荷载移动作用，其中一列车载离桥中心线距离为 e1，以速度v1从左向右移动，另一列车载离桥中心线距离为 e2，以速度v2从右向左相向而行。由此得到移动荷载作用下简支板桥的运动方程［10］：

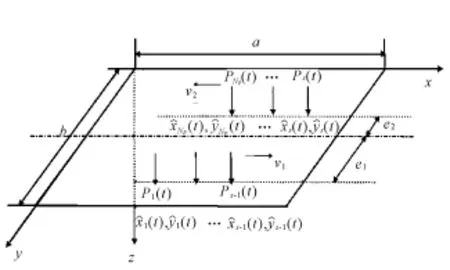
图1　移动荷载识别板桥模型

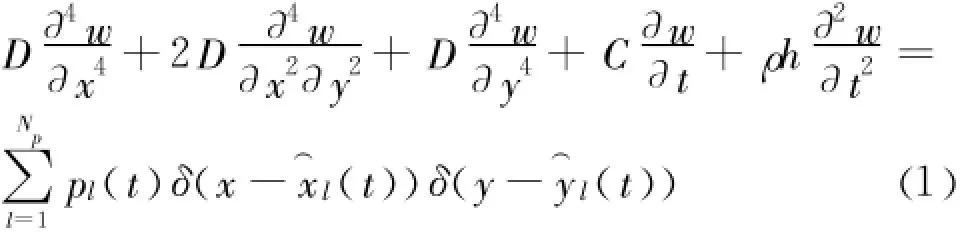
使用模态叠加法（分离参数），将板桥的竖向位移w（x，y，t）做如下处理并写成矩阵形式：其中：是板桥的振型 ；为广义模态坐标。

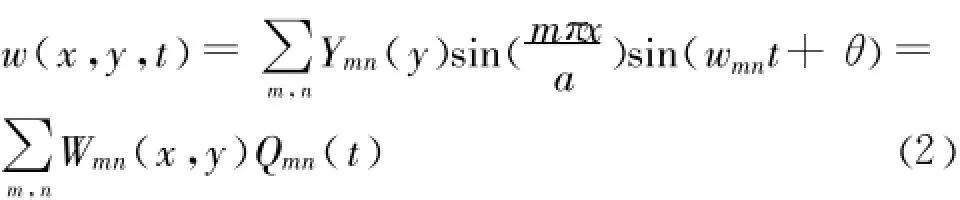
将式（2）代入式（1）可得：

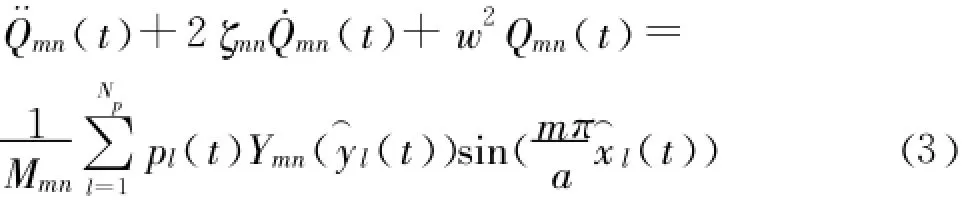
（m，n=1，2，3，4…分别为x方向和y方向的阶数）

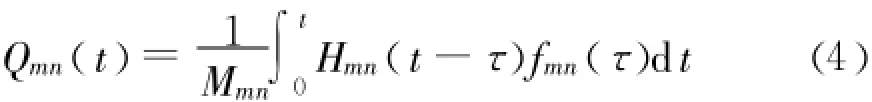
其中：

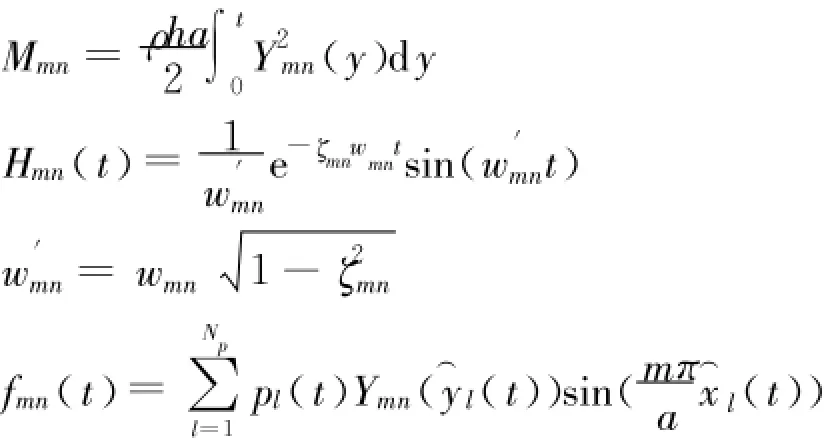
将式（4）带入式（2）并对w（x，y，t）的x向求二阶导数同时乘以中性轴到边缘的距离 h/2，离散化得到［11］：

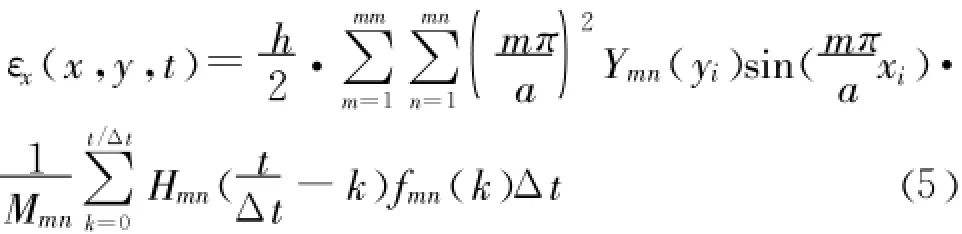
由此可见，方程的最终结果可以转化为矩阵形式：

式中：｛p｝是移动荷载的时间系列向量；｛ε｝桥面测点应变响应的时间系列向量；［A］是车桥系统相关的系数矩阵。

对式（6）进行Tikhonov正则化，转化为求解以下最小值问题［8］。

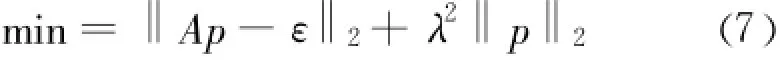
其中‖・‖为矢量的范数，λ＞0为正则参数。式（7）的解p满足如下方程：

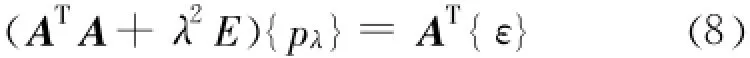
对A进行奇异值分解（SVD），如果 A的秩为n，则有：

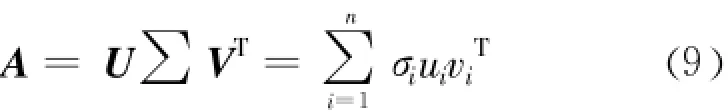
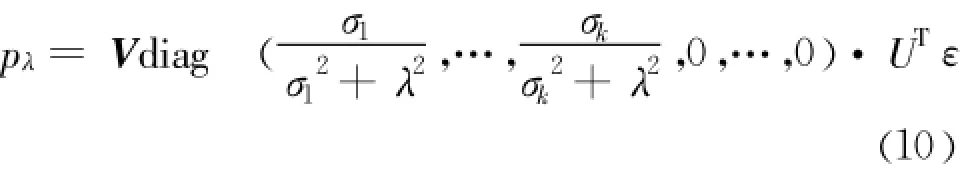
Tikhonov指出误差大小未知时，可根据下面的拟最优准则［12］来确定正则参数 λ。基本思想是：让正则参数λ以及正则解对该参数的变化率稳定尽可能小的水平，也就是寻找参数λ，使得：

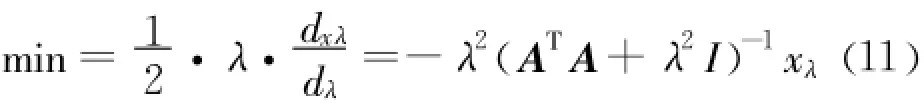
U=［u1，u2，…，um］∈Rm×m和V=［v1，v2，…，vn］∈Rn×n为正交矩阵 ，U的列向量为矩阵AAT的特征向量，V的列向量为矩阵ATA的特征向量。∑为m ×n阶伪对角阵，其前 n行diag｛σ1，σ2，…，σn｝，（σ1≥σ2≥…≥σn≥0）其后m-n行的元素都为0，σ1，σ2，…，σn为矩阵A的奇异值。则（8）式的解为：

将式（11）得到的λ代入式（10）中便可得到识别方程的正则化解。

2　实验研究

由于本文采用的是各向同性简支板桥识别理论，因此实验桥梁应尽量接近理想各向同性简支板桥，而实际运营桥梁中各向同性和简支边界很难保证。在实验室中的模拟实验采用的钢板保证了材料的各向同性，支座由两根钢管模拟，一根固定，一根自由滑动 ，与理想铰支座接近（图2），室内缩尺模型的环境噪声相对实桥来说较低，而且车辆数量和速度容易控制。

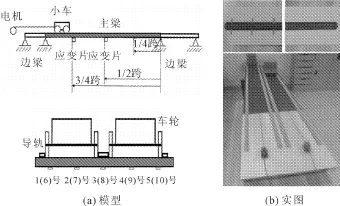
图2　实验模型

2.1实验模型及过程

本次实验采用的模型主要包括两部分：加载车辆及承重板，承重板为三跨简支板，两个边跨采用木板，用于车辆的加速和减速，中跨采用8 mm厚钢板，其计算跨径1.9 m，板宽52 cm，设计为双车道，两车道中心线间25.4 cm。加载小车轴距为24.5 cm，轮距14.4 cm。实验中选取主跨跨中截面和3/4截面作为测量截面，并在两个截面分别粘贴5个应变片并依次编号，跨中截面编号为1～5号，3/4截面编号为6～10号，全跨共布设10个应变片。实验模型如图2所示。数据采集系统是DH5922动态信号测试分析系统，采样频率为200 Hz。实验由前侧马达牵引小车前进 ，包括单辆小车单车道行驶和两辆小车以不同的速度不同的起始时间分别在两个车道上同向行驶。

2.2实验结果和测点影响线

2.2.1实验车辆动应变响应

图3是单独一辆小车在单侧车道行驶过程的动应变响应过程，各个波形对应的测点编号如图3所示。跨中1号，2号，4号测点的两个波峰分别表示车辆前后轴经过跨中截面时响应历程。对于3/4截面处的测点，两个车轴经过此处时，峰值应变并没有出现两个明显的波峰，而是呈现缓慢均匀增加的趋势，这与测点影响线中跨中截面应变单峰突起，3/4截面峰值应变变化平缓相一致。

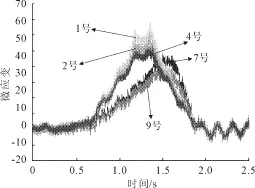
图3　单车道应变历程

图4是两辆小车在两个车道上同向行驶的测点应变历程图。跨中测点有5个波峰，其中第1、2、4、5个波峰为车轴经过跨中时的应变响应。第一辆小车前后轴经过跨中位置过程中，第二辆小车对测点应变的贡献越来越大 ，因此第2个波峰比第1个波峰明显要大。而第二辆小车前后轴经过跨中位置过程中，第一辆小车对测点应变的贡献越来越小 ，因此第4个波峰第5个波峰正好相反。在1号、2号和4号测点应变中，4号测点应变先由最小变为最大是由于两辆小车在不同的车道上出发的先后顺序不同引起的。9号测点也出现了相同的变化。

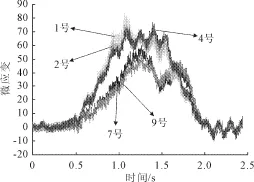
图4　双车道应变历程

2.2.2测点影响线

图5是通过公式（5）数值计算并拟合绘制的左侧车道7号测点不同模态数的应变影响线。从图中可以得知，识别模态数决定着应变影响线的变化形式。第3阶模态对于3/4截面处测点的应变影响线变化趋势影响最大，第6阶模态已经使影响线形态发生偏离。显然，模态数为2和6时影响线与实测数据不符，模态数为3、4、5时，影响线的应变值依次增大，但增加的幅度较小。由于识别模态数影响着识别精度，荷载识别精度随模态数的增加先增高后降低［9，13］，因此，本次影响线的识别模态选择前四阶。图6是取前四阶模态时各个测点的应变影响线，各测点的影响线均呈现出先上升后下降的趋势。

2.3车辆轴重反算

从影响线中取出相应数值和实验中获取的实测应变代入识别方程，并通过Tikhonov正则化方法计算就可以得到车辆轴重。由公式（10）可知正则参数λ取值成了荷载识别的关键。正则参数λ的大小不仅影响着方程解的误差还影响着解的稳定性。从误差的角度看，正则参数越小越好；而从稳定性的角度考虑，正则参数值越大越好［2］。本次计算过程采用的拟最优准则确定正则参数的方法，兼顾误差和稳定性，得到识别方程最优解。表1是选择不同测点和测点数的车辆轴重数值计算结果。从表1中可以看出数值计算正则参数 λ均小于10-7，说明方程正则解的误差较小。单车道前轴计算重量变化范围在3.0 kg～4.5 kg之间，而前轴的实际重量为3.7 kg。单车道车辆计算总重在10 kg～12 kg之间，实际重量为11.3 kg。识别荷载基本与小车实际荷载相吻合，其它各种工况下的与之类似。识别荷载变化不大说明通过Tikhonov正则化方法计算的车辆轴重稳定性较好。

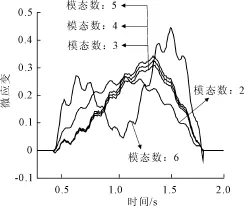
图5　7号测点不同模态数的应变影响线

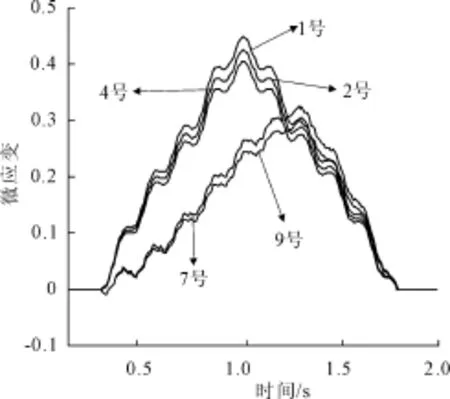
图6　测点应变影响线

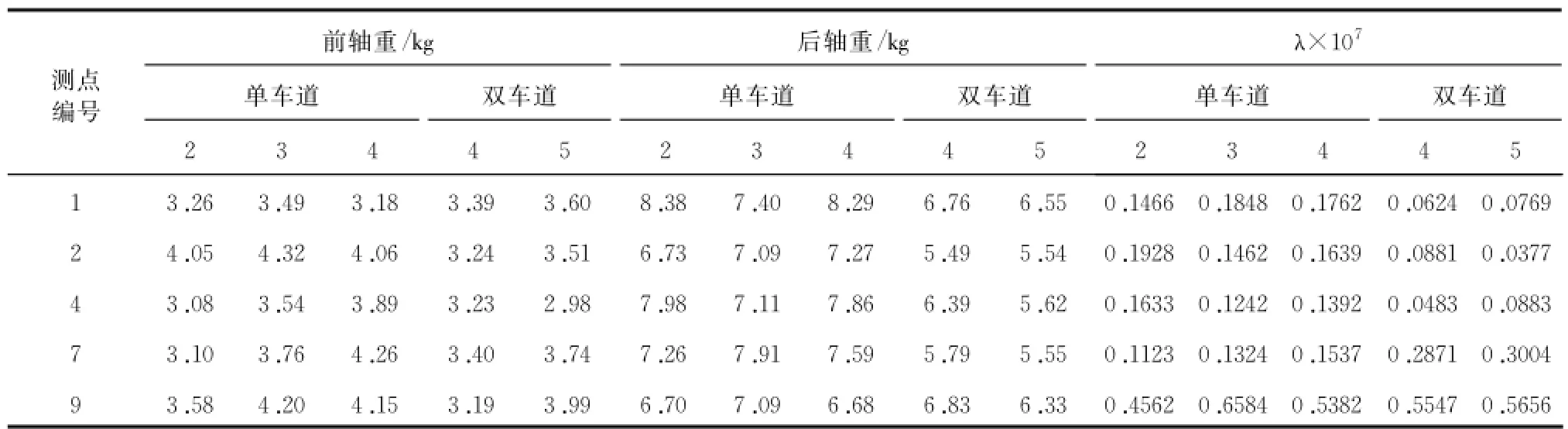
表1　车辆轴重识别结果

图7和图8是表1中的车辆轴重识别结果与实际值的对比图。从图7和图8可知，各种工况下，小车的识别轴重围绕实际轴重上下波动，并且变化幅度不大。单车道和双车道的荷载识别轴重与实际轴重标准差均小于0.6，识别荷载的离散程度不高。图8车辆1中后轴重最大相对误差为14.2%，车辆2中前轴重最大相对误差为15.1%。其它大部分相对误差在10%之内。满足车辆轴重初步识别要求。另外，由于测点应变选取的随机性 ，选择不同测点和测点数对荷载识别结果的影响比较大，这一点在图中表现得很明显。因此，在选取的数据时可以适当增加测点数，提高识别精度。

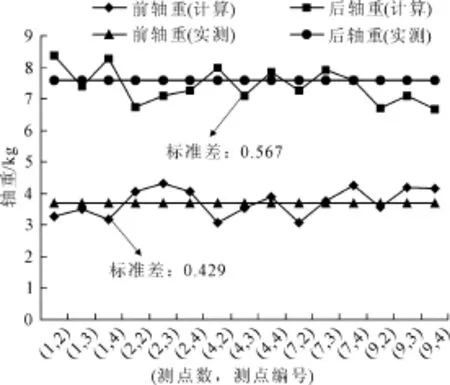
图7　单车道识别轴重与实际轴重对比图

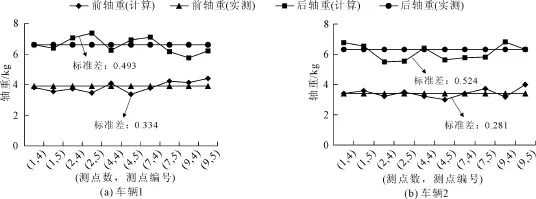
图8　双车道识别轴重与实际轴重对比图

3　结　论

（1）荷载识别理论中，将竖向位移分离成广义模态坐标和板桥振型的乘积，并由时域法积分获得振型函数，然后通过竖向位移得到荷载识别方程。对该方程进行Tikhonov正则化并根据拟最优准则选择最优正则参数值，则可得到识别方程的正则化解。这种方法兼顾解的误差和稳定性，降低病态方程的病态程度。

（2）为了验证理论的有效性，本文通过模型实验获取了简支板桥在车辆荷载作用下的应变响应，并将结果代入识别方程中进行反算。计算结果表明，识别荷载与实际荷载吻合较好，因此将Tikhonov正则化方法运用于荷载识别方程求解是有效的，并且识别精度较高，稳定性较好。

参考文献：

［1］李小年，陈艾荣，马如进.桥梁动态称重研究综述［J］.土木工程学报，2013，46（3）：79-85.

［2］朱南海.基于Tikhonov正则化和遗传算法的杆系结构荷载识别方法研究［D］.汕头：汕头大学，2008.

［3］范千，方绪华，范娟.病态问题解算的直接正则化方法比较［J］.贵州大学学报：自然科学版，2011，28（4）：29-32.

［4］肖庭延，于慎根，王彦飞.反问题的数值解法［M］.北京：科学出版社，2003.

［5］Phillips D L.A technique for the numerical solution of certain integral equations of the first kind［J］.Journal of the Association for Computing Machinery，1962，9（3）：84-97.

［6］Tikhonov A N.On solving incorrectly posed problems and method of regularization［J］.Doklady Akademii Nauk USSR，1963，151（3）：501-504.

［7］Zhu X Q，Law S S.Identification of vehicle axle loads from bridge dynamic response［J］.Journal of sound and vibration，2000，236（4）：705-724.

［8］Rowley C，Gonzalez A，O’Brien E，et al.Comparison of conventional and regularized bridge weigh-in-motion algorithms［C］//Proceeding of the Internation Converence on Heavy Vehicle.Paris，France：John Wiley，2008.

［9］李忠献，王波，陈锋.桥梁移动荷载的识别与参数分析［J］.福州大学学报：自然科学版 ，2005，33（S1）：56-61.

［10］Huffington N J，Hoppmann W H.On the transverse vibration of rectangular orthotropic Plates［J］.Journal of Applied Mechanics ASME，1958，25（2）：389-395.

［11］Zhu X.Vehicular load on bridge deck［D］.Hong Kong：Hong Kong Polytechnic University，2001.

［12］Tikhonov A N，Arsenin V Y.Solution of Ill-posed Problems ［M］.New York：John Wiley&Sons，1977.

［13］余岭，朱军华 ，陈敏中.基于矩量法的桥梁移动车载识别试验研究［J］.振动与冲击，2007，26（1）：16-20.

中图分类号：U446

文献标识码：A

文章编号：1672—1144（2015）03—0012—05

DOI：10.3969/j.issn.1672-1144.2015.03.003

收稿日期 ：2015-01-30修稿日期：2015-03-04

基金项目 ：中央高校基本科研业务费项目（2013121028）

作者简介 ：陈春苗（1988—），男，湖南郴州人，硕士研究生，研究方向为桥梁健康监测。E-mail：lovechen2012@foxmail.com

Experiment on Moving Load Identification Based on Tikhonov Regularization Method

CHEN Chun-miao，GAO Jing
（Department of Civil Engineering，Xiamen University，Xiamen，Fujian 361005，China）

Abstract：Based on the orthotropic plate theory and the modal superposition method，the load identification equations for simply supported slab bridges subjected to moving loads were deduced.Tikhonov regularization method was applied to solve the ill conditioned moving load identification equations，through which an optimal regularization parameter was selected to obtain the solution of regularization.In order to check the validity of Tikhonov regularization method，the moving loads identification model of a simply supported slab bridge was established in the experiment.The strain history was obtained when the model truck passed through the bridge at different speeds.Then，the measured data was substituted into the identification equations to get the load information.The calculation results indicate that the identification results are in good agreement with the actual weight of the model truck，which means that the Tikhonov regularization method is effective in obtaining a stable solution for load identification equations with improved accuracy.

Keywords：load identification；simply supported slab bridge；Tikhonov regularization method