非线性 Cosserat扩展模型及在地下岩体工程中的应用

张建成 ，贾金青，马英超

（大连理工大学海岸与近海工程国家重点实验室，辽宁大连116024）

非线性 Cosserat扩展模型及在地下岩体工程中的应用

张建成 ，贾金青，马英超

（大连理工大学海岸与近海工程国家重点实验室，辽宁大连116024）

摘要：由于Cosserat连续介质应力、应变张量的非对称性，经典的Mohr-Coulomb强度准则在Cosserat连续介质中不可直接应用，故需推导宜于Cosserat连续介质弹塑性有限元分析的Mohr-Coulomb强度准则，并将其应用于互层岩体Cosserat扩展本构模型。基于等向强化模型和增量型的塑性势理论，利用MATLAB平台分别编写Cosserat连续介质及经典连续介质的有限元程序，并对在互层岩体中开挖的洞室进行了变形分析。结果表明，对应力梯度不可忽略、弯曲效应比较明显的结构体，Cosserat介质法不仅计算更简便，而且有更好的适用性。

关键词：Cosserat理论；互层岩体；扩展模型；弹塑性有限元

20个世纪80至90年代，Cosserat理论开始应用于地下岩体工程领域。Adhikary、Mühlhaus［1-4］、佘成学、陈胜宏［5-6］及刘俊［7-8］等为验证该理论在岩土工程（特别是层状岩体）中的有效性、适用性及数值模拟等方面做了很多卓有成效的工作。由于层状岩体中顺层滑移和弯曲变形破坏等特点尤为突出，与经典连续介质理论相比，该理论能更好地分析层状岩体中的破坏现象。平面及空间状态下互层岩体的Cosserat扩展本构模型由李银平、杨春和等［9-10］建立而成。由于杨乐［11］利用王启耀［12］的层状岩体屈服条件过于简化，仅适用于两种岩层弹模相差较大的情况，通用性较差。本文基于弹塑性力学的张量理论，参照李育超等［13］推导宜于Cosserat介质的广义Mohr-Coulomb塑性屈服条件，并运用MATLAB数值模拟软件编写平面应变情形下Cosserat扩展模型的弹塑性有限元程序，并用算例验证了程序的有效性及模型的优越性。

1　二维Cosserat扩展模型

1.1二维Cosserat理论基本方程

Cosserat理论是Cosserat兄弟［14］于1909年首先提出，又称偶应力理论。其具有一定特征尺度的单元体上除受常规应力外 ，还有偶应力的作用。对于平面问题的单元体有两个平动分量和一个转动分量。

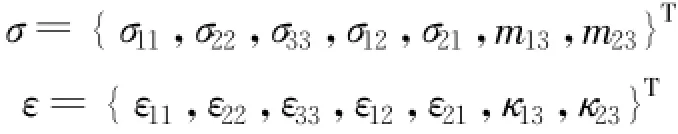
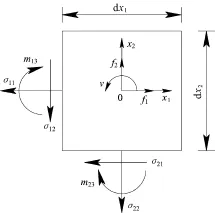
图1　单元体的广义应力

将Cosserat介质理论中单元体满足的平衡方程、几何方程、相容方程、边界条件以及本构方程用张量形式统一表示为

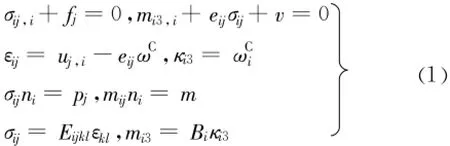
式中：fj、v分别为单元体的体积力、体积力偶；pj、m分别为单元体边界上的面力和面力偶 ；ωC为Cosserat单元体的转角；Eijkl、Bi为材料经典弹性常数；i、j均取1、2；eij为排列算子。

1.2Cosserat弹性扩展模型的本构关系［9-10，14-15］

地下岩体工程中常遇到互层岩体，即在两层岩体之间有一层较薄特性不同的岩体。单独模拟对其往往很难。对这种岩体，考虑具有不同力学特性相邻岩层之间的细观位移协调 ，引入偶应力，利用其非对称的应力、应变张量，建立宏观平均意义下考虑细观弯曲效应的Cosserat介质扩展本构模型。

在平面应变情况下，该模型由经典连续介质理论推导出Cosserat介质扩展的本构关系时利用三个假设，即连续性假设、平截面假设和小变形假设。模型中所取单元体包含两种物理性质不同、厚度不同的材料，如图2所示。

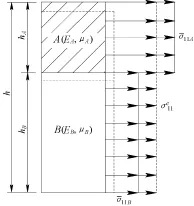
图2　层内正应力

在满足变形协调时，单元体中两种介质的厚度、物性均有不同，其上的正应力分布也不再均匀。故考虑将Cosserat应力类似地定义为沿 x2方向在单元体高度上的平均化：

我想起我在牢狱里度过的三年青春，不知道用什么来补偿。我说我真后悔当年那一砖头没砸死他，只让他缝了八针。是我，一浩说，那一砖头是我砸的。多年以来，我一直不能确定那一砖头到底是不是我砸的。除了一浩以外，所有人（包括我）都认为是我砸的。我只记得我站在那人面前，痛骂他，煽他耳光，用砖头砸他的摩托车。然后他大叫一声捂着后脑勺趴倒在地。一浩一直在他身后。回忆让事实更加清晰，我知道是一浩，但我自始至终坚持这一砖头是我拍的。那时一浩正复习考研。一浩说，是我，我一直很后悔，当时没敢承认。我说，一浩，别管谁砸的，都是为了我。一浩哭了，我搂住他的肩。

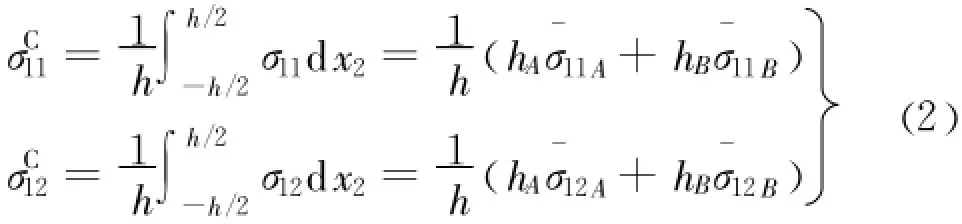
式中 ：¯σ11A、¯σ12A、¯σ11 B、¯σ12B分别代表各岩层应力的均值，上标“C”特指Cosserat介质点的量。

由于单元体中两岩层的弹性模量及泊松比均不同，为了满足前两个假设条件，应力分布沿整个截面不再是连续和等梯度的，如图3所示。

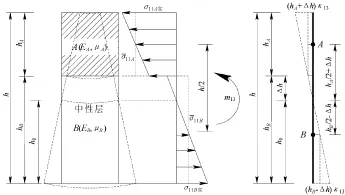
图3　复合层的偶应力与曲率

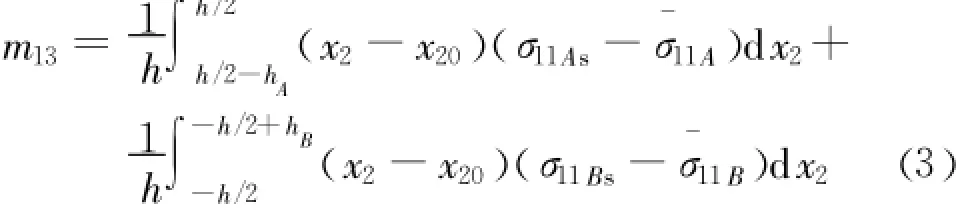
复合层的偶应力定义为：h/2式中的 σ11As、σ11 Bs分别代表A、B层的实际正应力 ；x20为“复合层”中性轴的位置。由于沿层面方向是均匀的，故没有考虑 m23作用。

建立Cosserat扩展模型的本构方程 ε=Cσ，其矩阵表达式为：

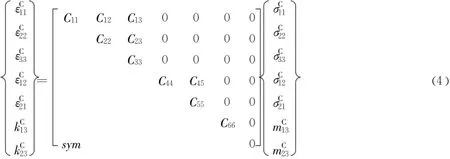
其中：式中：E′=E/（1-μ2）、μ′=μ/（1-μ），E、μ、G分别为经典意义上的弹性模量、泊松比与剪切模量；h 为A、B岩层厚度之和，α为体积分量：αA=hA/h；αB=hB/h。GC为Cosserat剪切模量。

2　Cosserat连续介质下的屈服条件［13］

屈服准则是用来确定塑性变形时的应力水平，经典理论中，屈服准则可通过三个应力不变量 I1、J2和 J3来表示：

F（σij，κ）=f（I1，J2，J3，κ）≤0（5）式中：κ是与材料有关的强化参数，或称内变量。

由于应力、应变张量在Cosserat介质中非对称，故需对传统的三个应力不变量进行修正。将Cosserat应变张量分为两部分，即对称与反对称：

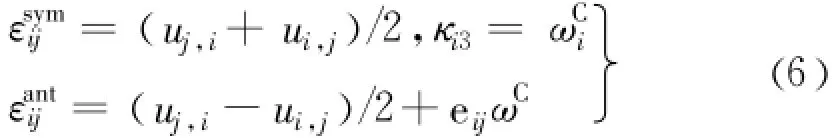
同样，Cosserat应力张量也可分为对称和反对称两部分：

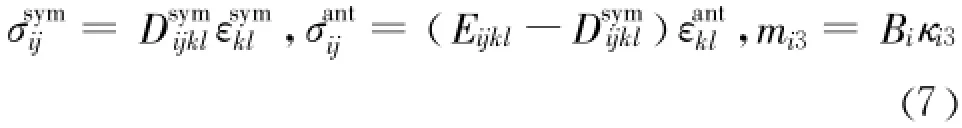
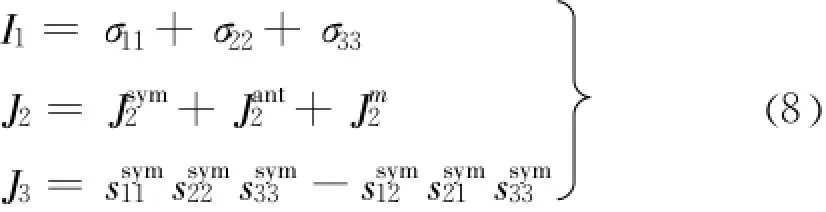
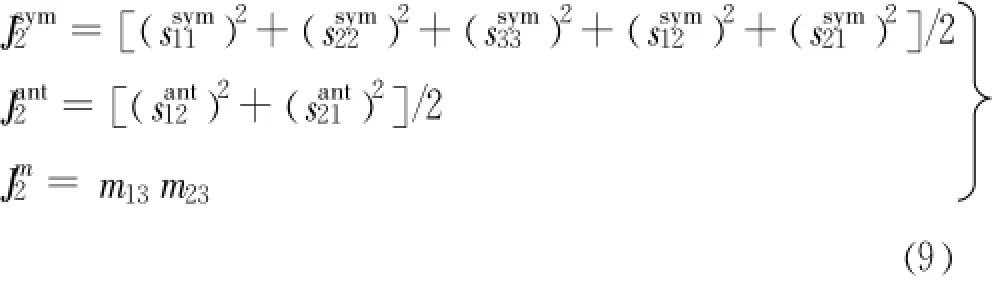
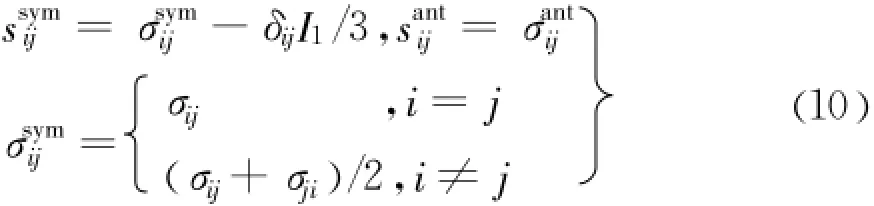
利用式（7），修正传统连续介质中的三个应力不变量：现假设Mohr-Coulomb（以下简称M-C）屈服函数仍可表示为应力不变量的函数，且形式与经典连续介质相同［13］。利用式（8），建立Cosserat连续介质下的M-C屈服准则：

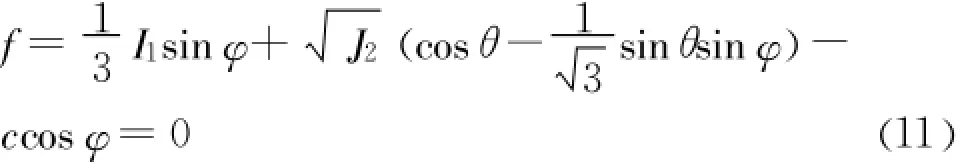
式中：c和φ分别为材料的黏聚力和内摩擦角；θ角的表达式为：I1、J2和 J3的表达式详见式（8）。

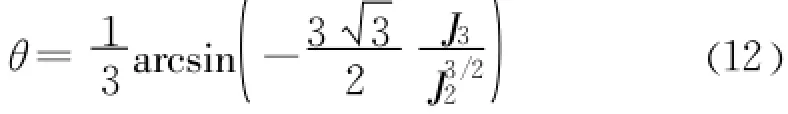
假设塑性应变满足相关流动法则，流动矢量a=∂f/∂σ，且σ是I1、J2和θ的函数，因而有

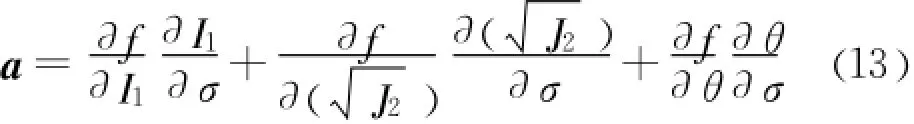
由式（12）可得：

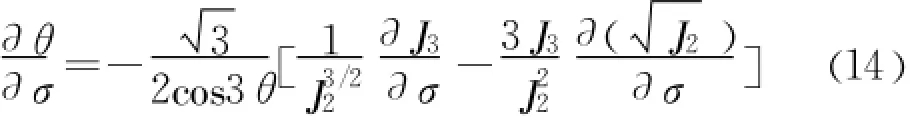
将上式代入式（13）得：

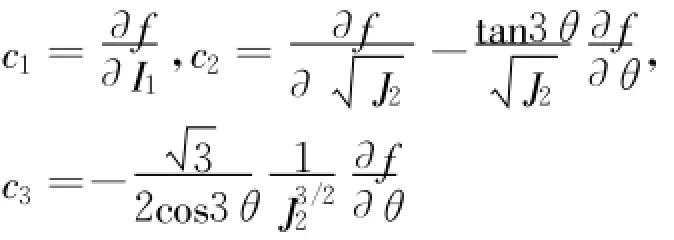
对于Cosserat连续介质理论的平面问题，a1、a2和 a3的表达式为：

于是，Cosserat连续介质下Mohr-Coulomb屈服准则的 c1、c2、c3表达形式如表1所示。

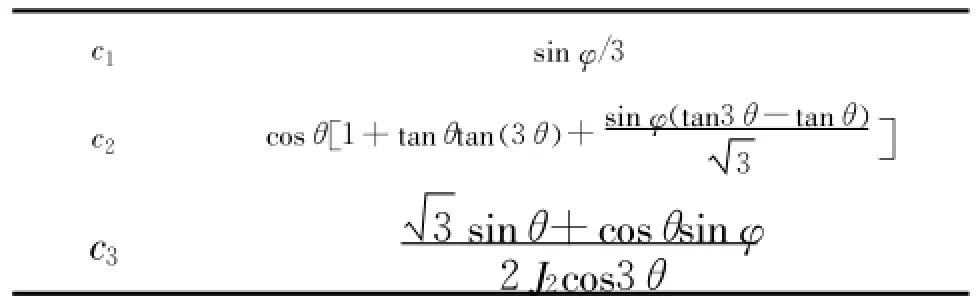
表1　Mohr-Coulomb屈服准则的 ci 值

3　算　例

某地下洞室工程下伏基岩为砂质泥岩与砂岩。砂质泥岩为主岩层，中间夹含砂岩层，地下洞室剖面的具体尺寸及各监测跟踪点如图4（a）所示。表2为软硬互层岩体基本参数。

表2　互层岩体的各项基本参数

运用MATLAB分别编写传统连续介质法和Cosserat介质法的弹塑性有限元程序对算例进行数值分析。计算域的边界取4倍于洞室孔径，范围是10 m×10 m，上覆岩层重量引起的3.5 MPa均布荷载作用。考虑结构及荷载均沿中轴线对称，故取其右半部分计算，如图4（b）所示。模型侧面为水平约束，底面为固定约束。

图5网格中的点代表在荷载作用下各单元中发生了塑性屈服的高斯点。计算结果见图6～图9、表3。

由最大主应力图6可知：最大拉应力产生于洞室的顶部、底部及边墙的中部；而最大压应力产生于洞室下方的两个拐角，其原因是由于此处洞室形状突变，应力集中所致。图6与图7（b）应力分布均显齿状，有明显层状形态，而其各自的（a）图由于Cosserat扩展模型的等效缘故，则显得比较平滑。

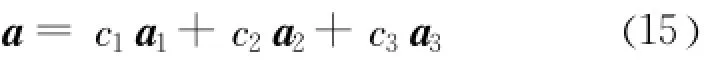
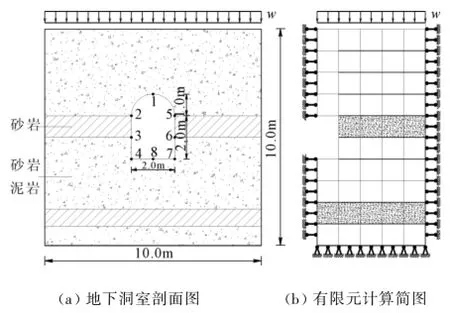
图4　地下洞室剖面和计算简图

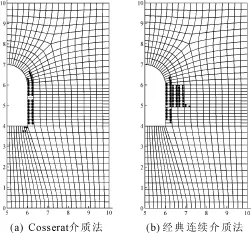
图5　塑性区分布图

图6　最大主应力分布图

图7　最大切应力分布图

由图8可见：洞室最大转角因应力集中 ，出现在形状突变区域，即洞室下方两个拐角及拱顶两侧；而图9清晰地显示出洞室的最大偶应力产生于洞室的顶部和底部的中间位置，这与在层状岩体中开挖地下洞室时往往在洞室的顶部和底部出现顶板弯折和岩层溃屈等破坏现象的位置是一致的。

由表3可知，各跟踪点均向洞室的内侧移动，2点、3点、4点分别与5点、6点、7点的水平与垂直向位移数值一致，但水平方向相反。Cosserat介质由于多考虑了偶应力的影响，弯曲效应明显。根据上述计算结果对比表明：在开挖面上，Cosserat方法在洞室顶部的垂直位移值要比传统连续介质方法大 ，而水平位移值前者要比后者小，更加接近于实际情况。

4　结　论

（1）通过对算例数值模拟的结果进行对比：Cosserat介质法与经典连续介质法相近，显示MATLAB编制的Cosserat弹塑性有限元程序的正确性。

图8　转角分布图/×10-5

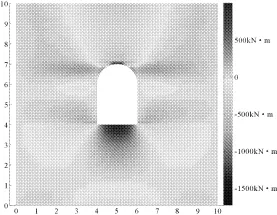
图9　偶应力分布图

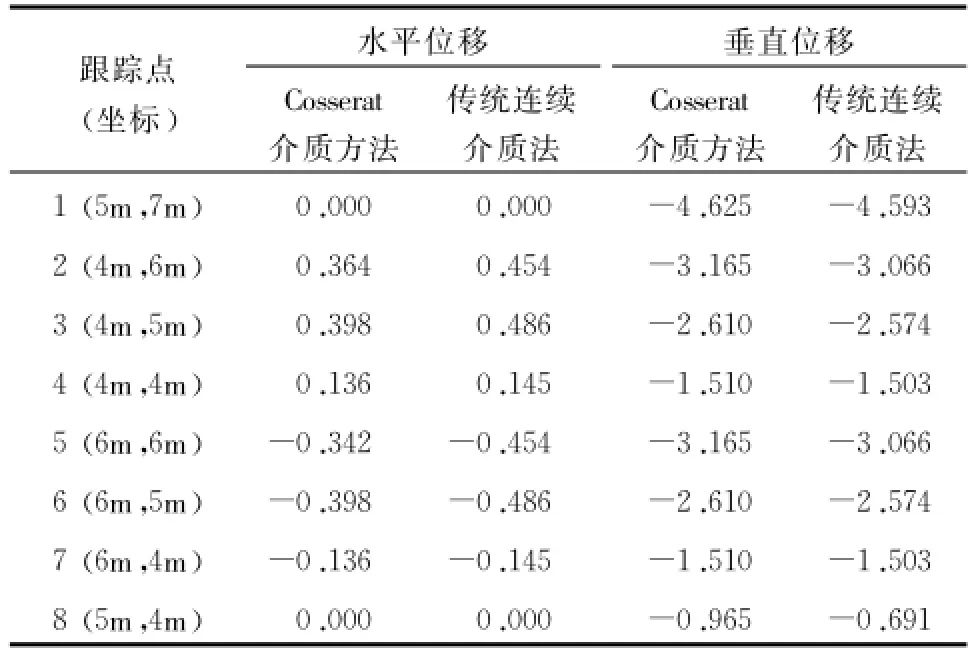
表3　弹塑性分析各跟踪点位移值　　单位：mm

（2）相较于经典连续介质法 ，Cosserat介质法的有限元网格无需细化，即可保证其计算精度 ，运用简便。

（3）由于Cosserat介质在单元体中多考虑了偶应力影响，故在层状岩体中模拟弯曲效应更明显。相较于经典连续介质法，Cosserat介质法计算的塑性区不仅出现在洞室开挖面的边墙，而且在其顶部与底部也发生了屈服。同时，在开挖面的洞室顶部，Cosserat介质法比经典连续介质法计算的垂直位移更大，而水平位移变化却比后者小。这些均表明：Cosserat介质法计算的结果更接近于实际情况。

综上 ，对于互层岩体，Cosserat扩展模型不仅可行，且能带来较大便利。

参考文献：

［1］Adhikary D P，Dyskin A V.Modelling the deformation of underground excavations in layered rock masses［J］.International Journal of Rock Mechanics and Mining Sciences，1997，34（3）：714-725.

［2］Adhikary D P，Mühlhaus H B，Dyskin A V.A numerical study of flexural buckling of foliated rock slopes［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2001，30（2）：871-884.

［3］Adhikary D P，Mühlhaus H B，Dyskin A V.Modelling the large deformations in stratified media the Cosserat continuum approach［J］.Mechanics of Cohesive Frictional Materials，1999，4（3）：195-213.

［4］Adhikary D P，Dyskin A V.A Cosserat continuum model for layered materials［J］.Computers and Geotechnics，1997，20 （1）：15-45.

［5］佘成学，熊文林，陈胜宏.具有弯曲效应的层状结构岩体变形的Cosserat介质分析方法［J］.岩土力学，1994，15 （4）：12-19.

［6］佘成学，熊文林，陈胜宏.层状岩体的弹粘塑性Cosserat介质理论及其工程应用［J］.水利学报，1996，（4）：10-17.

［7］刘俊，陈胜宏.节理岩体三维偶应力弹性理论［J］.岩土力学，1995，16（4）：20-29.

［8］刘俊，黄铭，葛修润.Cosserat介质理论针对节理岩体的应用［J］.岩土力学，2004，25（S2）：27-31.

［9］杨春和，李银平.互层盐岩体的Cosserat介质扩展本构模型［J］.岩石力学与工程学报 ，2005，24（23）：4226-4232.

［10］李银平，杨春和 .层状盐岩体的三维Cosserat介质扩展本构模型［J］.岩土力学 ，2006，27（4）：509-513.

［11］杨乐 ，许年春，谢贵平，等.层状岩体地下洞室的Cosserat理论有限元分析［J］.岩土力学 ，2010，31（3）：981-985.

［12］王启耀，蒋臻蔚 ，杨林德.层状岩体巷道弯曲变形的有限元模拟［J］.岩土力学 ，2006，27（7）：1101-1104.

［13］李育超，凌道盛 ，陈云敏.Cosserat连续介质的Mohr-Coulomb屈服准则及其应用［J］.浙江大学学报：工学版，2005，39（2）：253-258.

［14］Cosserat E.&F.Théorie des Corps Déformables［M］. Paris：Herman et Fils，1909.

［15］张建成.Cosserat介质弹性理论的有限单元法［D］.南京：河海大学，2012.

中图分类号：TU45

文献标识码：A

文章编号：1672—1144（2015）03—0066—06

DOI：10.3969/j.issn.1672-1144.2015.03.013

收稿日期 ：2015-01-11修稿日期 ：2015-04-16

基金项目 ：国家自然科学基金资助项目（51078059，51178078）

作者简介 ：张建成（1984—），男，江苏连云港人 ，博士研究生 ，研究方向为岩石力学与工程。E-mail：zjc15951087073@126.com

Nonlinear Cosserat Expanded Constitutive Model and Its Application of Underground Rock Engineering

ZHANG Jian-cheng，JIA Jin-qing，MA Ying-chao
（State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China）

Abstract：Classical yield criterion of Mohr-Coulomb cannot be directly applied to Cosserat continuum due to the asymmetry of the strain and stress tensors in Cosserat continuum theory.Therefore，the application of the Mohr-Coulomb yield criterion in the Cosserat continuum expanded constitutive model was established.On the basis of the isotropic hardening and incremental plastic potential theory，the elasto-plastic finite element codes for the Cosserat expanded constitutive model and classic continuum model were developed by using MATLAB.Then，it was applied to flexural deformation analysis of the underground cave excavated in interlayered rock mass.The results suggest that the Mohr-Coulomb-based Cosserat medium method is simpler and more applicable for the structures with obvious stress gradient or bending effect. Keywords：Cosserat continuum theory；interlayered rock mass；expanded constitutive model；elasto-plastic FEM