典型无压长隧洞恒定渐变流水面线计算的新解析法

王贺瑶，黄朝煊

（1.浙江省宁波市宁海县水利局，浙江宁波315600；2.浙江省水利水电勘测设计院，浙江杭州310002）

典型无压长隧洞恒定渐变流水面线计算的新解析法

王贺瑶1，黄朝煊2

（1.浙江省宁波市宁海县水利局，浙江宁波315600；2.浙江省水利水电勘测设计院，浙江杭州310002）

摘要：针对现有水面线计算采用的逐段试算法计算较繁琐等问题 ，对典型无压长隧洞如城门洞形、卵形无压隧洞恒定渐变流沿程水深的计算进行了数学推导。根据渐变流水力微分方程，利用数值计算理论及无量纲化原理，将恒定渐变流基本微分方程转换为高精度的可解析积分函数形式，进而得到典型无压长隧洞水面线计算得解析式，利用该解析式可直接算得沿程水深。该解析算法比《水工隧洞设计规范》建议的逐段试算法更简捷，并通过工程算例分析，该新解析法成果精度可靠，方便快捷，完全满足工程实践要求。

关键词：恒定渐变流；城门洞形断面；卵形断面；断面水力要素

对典型无压隧洞恒定渐变流水面线计算，文献［1-3］中均推荐采用基于差分格式的分段求和试算法，其水面线计算较复杂，需借助计算机进行迭代试算求解，张建民等［4］得出收敛迭代算法，国内外众多学者提出Runge-Kutta法、Newton迭代法等多种算法［5］，但这些算法大多均是利用逐段试算各段面水深的思路 ，这种计算理念可能导致误差积累效应。黄朝煊［6］对梯形断面水力特性也进行了探讨，黄朝煊［7］对梯形明渠水面线进行了研究，黄朝煊［8-9］分别对圆形、马蹄形无压隧洞水面线进行了尝试性探讨。水面线计算中特征水深如临界水深、正常水深计算也很重要，其中王正中等［10］对马蹄形断面隧洞

由于基于差分法的分段求和试算法需利用软件编程计算，工作量大，不利于工程手算推广。因此，该文根据渐变流水力学微分方程，利用MATLAB软件编程计算［14-16］，推导出流程 S与始、末断面水深之间的解析计算式，进而可利用该解析式直接计算沿程各断面的水深。

1　无压长洞的渐变流微分方程

1.1恒定渐变流水力微分方程

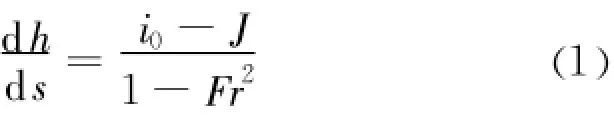
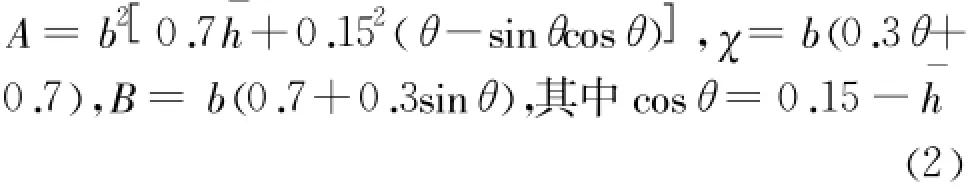
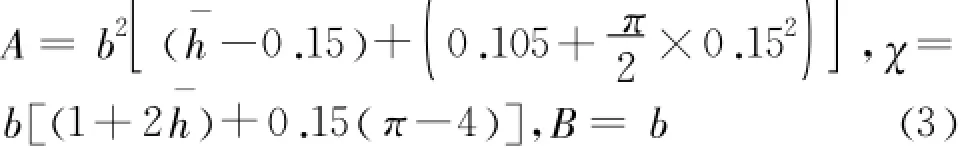
当0.15b＜h＜d时，其水力要素为：；B为水面宽度（m），A为断面过水总面积（m2），R为过水断面的水力半径（m）；J为过水断面水力坡降；n为隧洞底坡平均糙率；Q为隧洞过流流量（m3/s）；v为过水断面流速（m/s）；Fr为断面弗汝德数。

（1）典型城门洞形断面

当0＜h≤r1=0.15b时，其水力要素为：

当 h≥d时，其水力要素为：

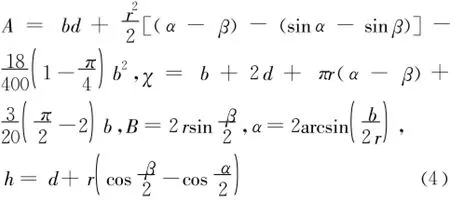
式中：b为过水断面底宽（m）；h为过水断面水深（m）；d为城门形断面直墙段墙高（m）；r为城门形断面顶部圆弧半径（m）；α为城门形断面顶部圆弧总中心角（rad）；β为过水断面水面处圆弧中心角（rad）。本文依据新版《水工设计手册》中典型城门洞断面（见图1），选取d=0.5b、α=2π/3时的典型断面分析。

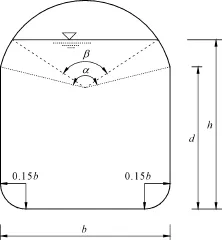
图1　城门洞型无压长隧洞断面图

（2）典型卵形断面（见图2）

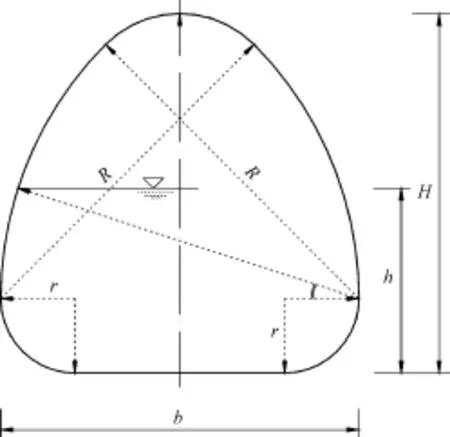
图2　卵形无压长隧洞断面图

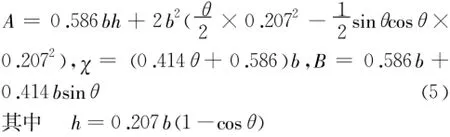
当 h＞r2=0.207b时，其水力要素为：

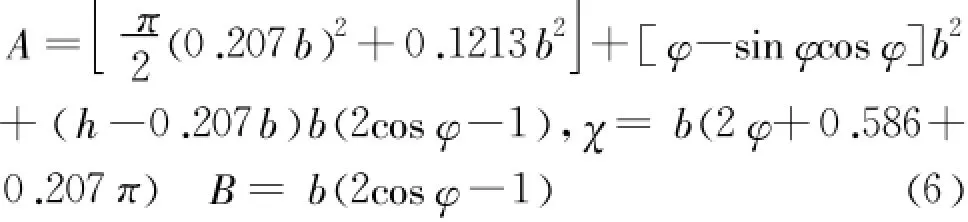
其中 h=0.207b+bsinφ

根据规范［3］，对于无压长隧洞，过水断面顶部净空面积应不小于总断面面积的15%，并且顶部净空高度不小于0.4 m。

当水深较浅0＜h≤r2=0.207b时，其水力要素为：

1.2无纲量函数的数值计算分析

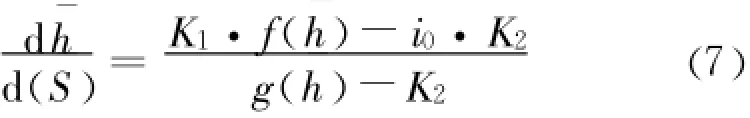
（1）典型城门洞形断面

对于典型城门洞形断面即 d=0.5b、α=2π/3时，无纲量函数f（¯h）、g（¯h）是相对水深¯h=h/b之间的函数 ，分析函数 f（¯h）、g（¯h）的变化关系，见图3。

（2）典型卵形断面

对于典型卵形断面，无纲量函数 f（¯h）、g（¯h）是相对水深 ¯h=h/b之间的函数，分析函数 f（¯h）、g（¯h）的变化关系，见图4。

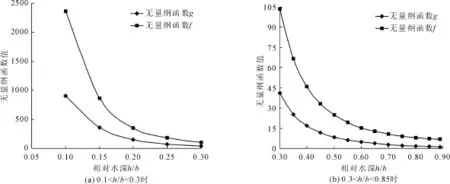
图3　典型城门洞型断面无量纲函数 f（¯h）、g（¯h）与¯h=h/b关系

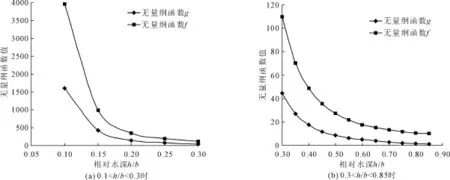
图4　典型卵形断面无量纲函数 f（¯h）、g（¯h）与¯h=　h/b关系

利用Matlab软件数值计算分析，利用形式简单、可解析积分的双曲函数对无量纲函数进行高精度数值拟合，数值拟合公式如表1所示，为了简化记函数为：

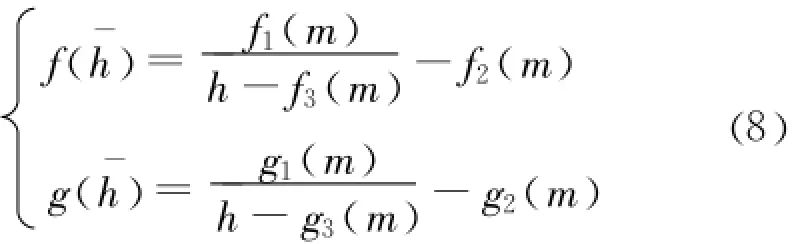
1.3渐变流水面壅、降趋势分析

根据文献［1］可知，明流下恒定渐变流水面线的壅、降变化可分为以下三种情形：

第1区，当满足条件：h＞hk且h＞h0时，该区内水面线属于壅水线。

第2区，当满足条件：hk＜h＜h0或h0＜h＜hk时，该区内水面线属于降水线。

第3区，当满足条件：h＜hk且h＜h0时，该区内水面线属于壅水线。

1.3.1典型城门形断面特征水深分析

对城门形无压隧洞的正常水深 h0解析算式分析，众多学者对其进行了研究，但算式较复杂，本文利用Matlab软件进行数值计算，给出了简洁的解析

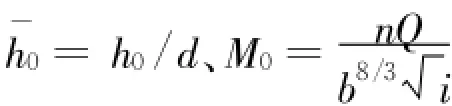
算式，记：，通过CurveExpert软件拟合得相对正常水深的高精度计算表达式：

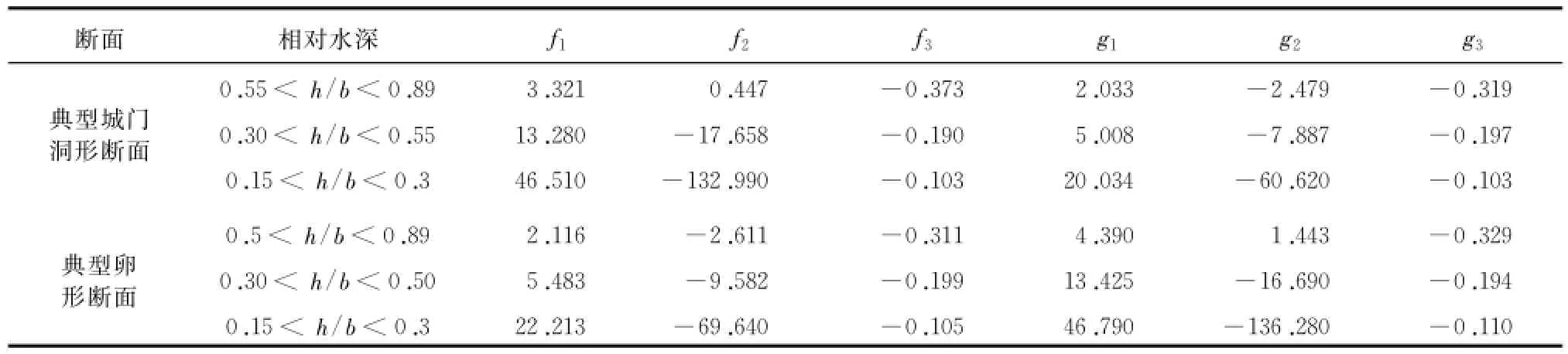
表1　典型无压长洞无纲量函数 f（¯h）、g（¯h）与相对水深¯h=h/b 高精度拟合参数

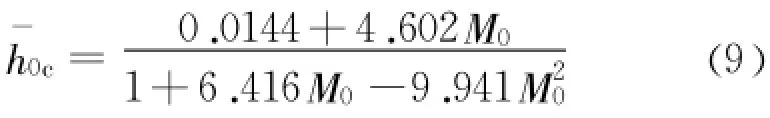
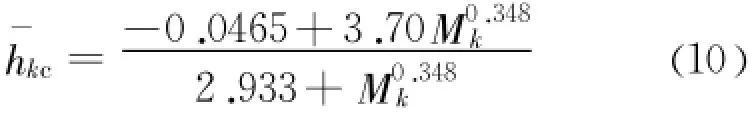
典型城门形断面特征水深曲线见图5。

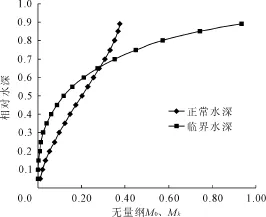
图5　典型城门形断面特征水深曲线图

1.3.2典型卵形断面特征水深分析

笔者暂未见有深入研究，本文以相对水深作用待求变量，设无量纲量：同上文，通过CurveExpert软件拟合得相对正常水深的表达式：

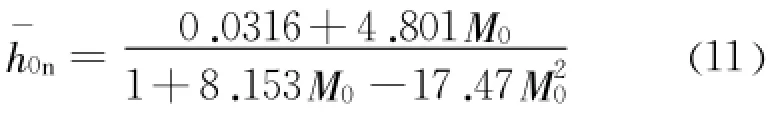
笔者暂未见有深入研究，本文重新给出卵形隧洞的临界水深计算公式（设无量纲量同上文）：典型卵形断面特征水深曲线见图6。

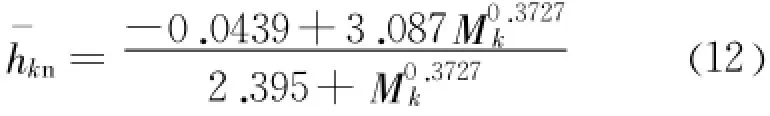
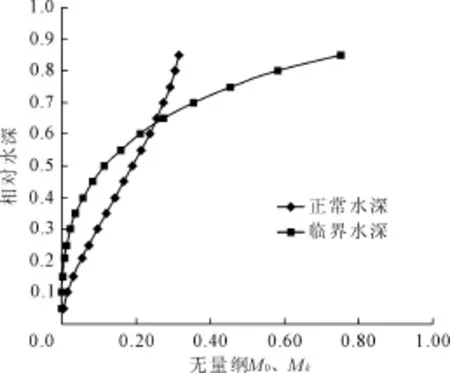
图6　典型卵形断面特征水深曲线图

1.4无压隧洞恒定渐变流水面线计算的解析解

将高精度拟合函数 f（¯h）、g（¯h）代入方程（7）：

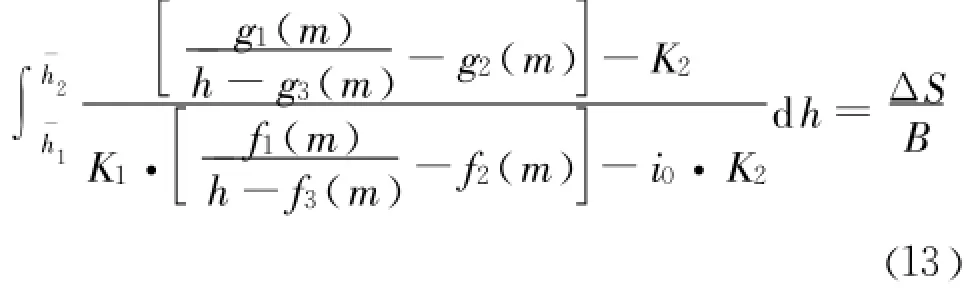
变化以上微分方程为简单函数积分形式：

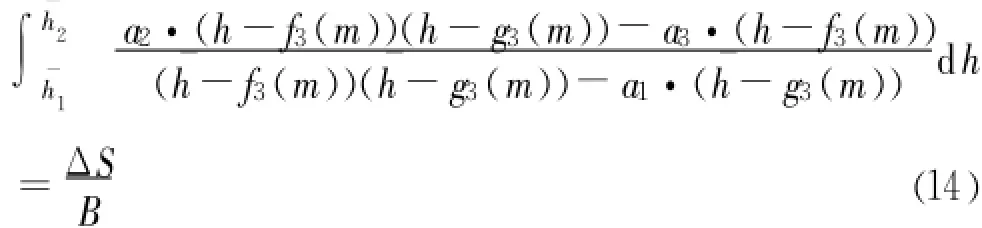
积分方程式（14）得：

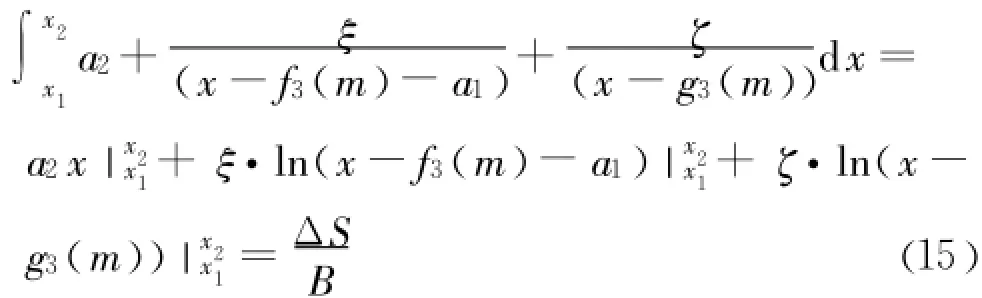
其中常参数：

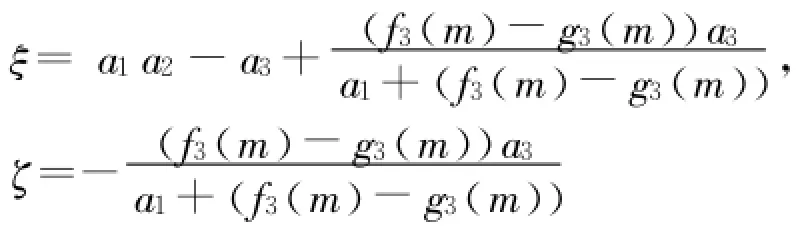
最后，得恒定渐变流沿程水面线应满足以下解析函数：

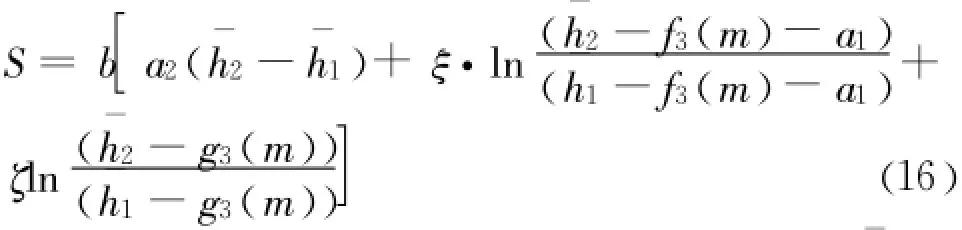
式中：S为流程（m）；常数 a1、a2见式（14）；¯h1= h1/b、¯h2=h2/b，为相对断面水深；ξ、ζ见式（15）；拟合常数 f3（m）、g3（m）可查表1。

本文沿程水深直接算式（16）计算简单快捷，精度可靠。

2　算例分析

算例1：某长距离输水无压隧洞过水断面为典型城门洞型，见图1所示，隧洞顶的半圆直径 d=3 m，隧洞底部平均坡比0.0137，糙率0.015，设计流量25.47 m3/s，起始断水深1.80 m，无压输水隧洞长1 km，按无压“长洞”计算，试求沿程各断面水深。

根据式（9）可求正常水深：M0=0.1741，h0= 1.35 m，根据式（10）可求临界水深：Mk=0.2723，hk=1.95 m。属第2区，利用式（16）可直接求得沿程降水水面线，fi（m）、gi（m）查表1，成果见图7。

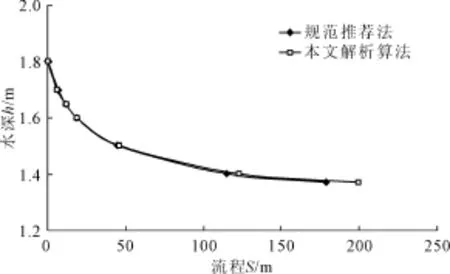
图7　算例1水面线曲线图

算例2：某长距离输水无压隧洞过水断面为典型卵型，见图2所示，b=3 m，隧洞底部平均坡比0.0149，糙率0.015，设计流量25.57 m3/s，起始断水深1.80 m，无压输水隧洞长1 km，按无压“长洞”计算，试求沿程各断面水深。

根据式（11）可求正常水深：M0=0.1081，h0= 1.35 m。根据式（12）可求临界水深：Mk=0.2747，hk=1.95 m。属第2区，利用式（16）可直接求得沿程降水水面线，fi（m）、gi（m）查表1，成果见图8。

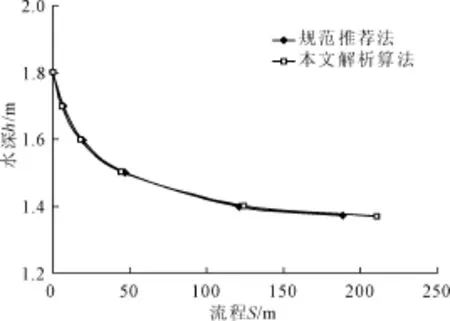
图8　算例2水面线曲线图

根据以上计算比较可知 ，本文断面水深直接计算式（16）精度可靠、方便快捷，便于工程师应用推广。

3　结　语

针对现有水面线计算采用的逐段试算法计算较繁琐等问题，对典型无压长隧洞如城门洞形、卵形无压隧洞恒定渐变流沿程水深的计算进行了数学推导，主要结论如下：

（1）根据渐变流水力微分方程，利用数值计算理论及无量纲化原理，将恒定渐变流基本微分方程转换为高精度的可解析积分函数形式，进而得到典型无压长隧洞水面线计算的解析式。

（2）通过多个算例分析，利用推求得解析式可直接算的沿程水深 ，并与规范推荐的逐段试算法成果进行了比较，认为本文新解析法成果精度可靠，方便快捷，完全满足工程实践要求。

参考文献：

［1］武汉大学水利水电学院.水力计算手册［M］.北京：中国水利水电出版社，2006.

［2］中华人民共和国水利部.SL253-2000.溢洪道设计规范［S］.北京：中国水利水电出版社，2000.

［3］中华人民共和国国家发展和改革委员会.DL/T5195-2004.水工隧洞设计规范［S］.北京：中国水利水电出版社，2004.

［4］张建民，王玉蓉，等.恒定渐变流水面线计算的一种迭代方法［J］.水利学报，2005，36（4）：501-504.

［5］万五一，江春波，等.变步长法在天然河道水面线计算中的应用［J］.哈尔滨工业大学学报，2007，39（4）：648-650.

［6］黄朝煊，王贺瑶，王正中，等.消力池最不利条件下池深极值探讨［J］.水力发电学报，2015，34（1）：79-84.

［7］黄朝煊.梯形渠道恒定渐变流水面线计算的新解析法［J］.长江科学院院报，2012，29（11）：46-49.

［8］黄朝煊.圆形无压隧洞恒定渐变流水面线计算的近似法［J］.灌溉排水学报，2012，31（5）：113-117.

［9］黄朝轩.马蹄形无压隧洞恒定渐变流水面线计算的新解析法［J］.中国农村水利水电，2012，（10）：91-94.

［10］王正中，陈涛，芦琴，等.马蹄形断面隧洞临界水深的直接计算［J］.水力发电学报，2005，24（5）：95-98.

［11］赵延风，宋松柏，孟秦倩.普通城门洞形断面临界水深的近似计算方法［J］.长江科学院院报，2008，25（4）：14-15. ［12］张宽地，王光谦，吕宏兴，等.明流条件下城门洞形隧洞临界水深的直接计算法［J］.四川大学学报：工程科学版，2010，42（3）：102-106.

［13］张宽地，吕宏兴，王光谦，等.普通城门洞形隧洞正常水深的直接计算方法［J］.农业工程学报，2009，25 （11）：8-12.

［14］龚纯，王正林 .精通Matlab最优化计算［M］.北京：电子工业出版社 ，2009.

［15］王沐然.Matlab与科学计算（第二版）［M］.北京 ：电子工业出版社，2011.

［16］张志涌.精通matlab R2011a［M］.北京：北京航天航空大学出版社，2011.

中图分类号：TV133+.1

文献标识码：A

文章编号：1672—1144（2015）03—0077—05

DOI：10.3969/j.issn.1672-1144.2015.03.015

收稿日期 ：2015-01-05修稿日期 ：2015-02-06

基金项目 ：水利部公益性行业科研专项项目（201401010）；围垦院软基水闸创新团队科标业项目

作者简介 ：王贺瑶（1979—），女，辽宁清原人，硕士 ，主要从事水工结构方面的研究工作。E-mail：3994528@qq.com临界水深进行了研究并给出了解析算式，赵延风等［11］给出了普通城门洞形断面临界水深的近似计算方法 ，张宽地等［12］给出了明流条件下城门洞形隧洞临界水深的直接计算法 ，张宽地［13］给出了普通城门洞形隧洞正常水深的直接计算方法，根据这些特征水深，能快速定位水面线的壅、降趋势。

A New Analytical Method of Caculating Water Surface Profile of Gradually Varied Steady Flow for Typical Long Tunnels Without Pressure

WANG He-yao1，HUANG Chao-xuan2
（1.Zhejiang Ninghai County Water Conservancy Bureau，Ningbo，Zhejiang 315600，China；2.Zhejiang Design Institute of Water Conservancy&Hydro-electric Power，Hangzhou，Zhejiang 310002，China）

Abstract：The existing analytical method for calculating water surface profile adopts section by section trial calculation which is tedious and inconvenient.Here the gradually varied steady flow depth of the typical long non-pressure tunnels with horseshoe-shaped cross-section and oval cross-section was mathematically deduced，and then its basic differential equation was transformed into an analytical integral function with high-precision based on the numerical analysis theory and dimensionless principle，from which the analytical formula for calculating water surface profile of gradually varied steady flow for typical long non-pressure tunnels was obtained.The water depth can be calculated directly according to this formula and it’s more convenient and simple than the recommended method in the specification for design of hydraulic tunnel.According to the analysis of its application in an actual construction project，this method is more convenient and simple，and it can provide more accurate and reliable results that meet the requirements of the construction.

Keywords：gradually varied steady flow；horseshoe-shaped cross-section；oval cross-section；section hydraulic elements