某学院 13#学生公寓 Push-over分析

李　涛

（商洛学院城乡规划与建筑工程学院，陕西商洛726000）

某学院 13#学生公寓 Push-over分析

李涛

（商洛学院城乡规划与建筑工程学院，陕西商洛726000）

摘要：静力弹塑性分析方法（Push-over分析法），由于操作方便、实践性强、准确度高等优点，是国内外广大科研工作者及设计人员所接受的结构抗震能力的评估方法。基于Push-over的基本原理，对侧向力模式、破坏形式及 P-Δ效应等能够对分析结果产生重大影响的参数设置进行了探讨，最后利用有限元软件Sap2000 v15对一框架结构进行了简单的设计验算 ，计算结果与已有研究结果吻合相对较好。结论表明，运用该软件对类似结构进行静力弹塑性分析能够满足相应规范的规定 ，且安全系数相对较高。

关键词：静力弹塑性；侧向荷载；破坏形式；P-Δ效应；塑性铰

传统的结构抗震设计往往采用的是基于承载力的方法进行，然而试验证明，当侧向力使结构进入塑性变形阶段后，承载力相对保持不变，但侧向位移却持续增加，显然基于承载力的设计方法已不适用于此阶段的设计［1-2］。而在资源短缺、环境恶化与地震频发的今天，如何有效准确的评估震后进入塑性阶段建筑物的性能，已成为亟待解决的大问题，因此基于性能的结构抗震设计方法便应运而生［3-4］。

Push-over分析法，就是在此情况下产生的基于性能评估现有结构和设计新结构的一种方法，又称为静力弹塑性分析法（Nonlinear Static Procedure）。尽管此方法在结构等效振型、目标位移的确定等方面存在着缺陷，但却具有方便操作，简单实用，与事实结合良好等优势 ，受到了现今研究人员与工程技术人员的广泛关注［5-7］。本文以商洛学院新建13号学生公寓为例，运用弹塑性有限元分析软件Sap2000v15阐述Push-over基本原理及其分析中应注意的事项。

Push-over分析法是以两个基本假定为基础［8］的，即：假定1：对原结构进行简化，用一等效自由度来代替多自由度体系的实际工程结构；假定2：结构向量Φ控制整个高度方向上的结构变形，并且在整个反应过程中保持不变。虽说在实际过程中与两个假定存在着一定的差距，但是已有的研究成果表明，采用此假定能够合理的估算结构的最大地震反应，因此尚一直沿用［9-10］。

基于此，根据实际情况，给结构施加一定方式布置的水平侧向力，之后持续增加侧向力，直至某些构件进入塑性，使结构的整体特性发生改变 ，再反过来又对水平侧向力的大小与分布进行调整，依次交替下去，直到结构达到目标位移。水平侧向力的大小是根据结构在不同阶段的周期由设计反应谱求得，而其分布则主要是根据结构的振型求得。理论上为当进入塑性阶段后，对进入塑性的构件刚度矩阵进行归零，并对整体刚度矩阵进行修正，再反过来调整水平侧向力的大小与分布 ，直至达到预定的破坏，而手工计算比较繁琐，因此现阶段主要借助于有限元思想，运用设定的程序进行分析计算，例如Sap2000、ETABS、Ansys等。

1　参数设置

1.1侧向力分布模式

理论上，侧向力的分布模式应能够合理的反映地震过程中结构的实际惯性力分布，并且使所求得的位移大体上能反映真实地震作用下结构的位移状况。但在实际的Push-over分析中很难做到，通常情况借助于弹性体系的振型分解反应谱的概念，将各振型下的水平地震力近似看作静力荷载施加于结构上［11］，而常用的加载模式分为四类，即均匀分布、倒三角分布、指数分布与多振型分布。其中，前三种分布为固定型加载模式 ，即在整个Push-over加载过程中，加载模式自始至终不变，不考虑由于结构自身刚度的变化而引起的惯性力的重分布；而多振型分布为适应型加载模式，是随结构惯性力的不同，根据变形过程中结构周期的改变，不断的调整加载模式。理论上后者更为合理，但相对较为复杂。实践证明，运用固定型加载模式 ，可以使计算过程大为简化，也可得到工程中允许的计算精度。

1.2破坏形式

结构的内力和变形随着侧向力的增加而不断增大，在一些受力较大部位，应力集中造成构件进入屈服阶段，变形显著增加。此时，在此部位的一定长度内形成了一个“铰”，称为“塑性铰”；当变形持续增加，而致使杆件的两端或是跨中再次出现“铰”，则构件的破坏机构形成，此时不能再承受荷载。在进行Push-over分析时，此铰的选取与构件的恢复力模型是紧密相连的。因此，在整个分析计算中占据着重要地位 ，常见的破坏机构有以下三种［12］。

图1（a）为一较理想的破坏形式，塑性铰即首先出现在梁端和底层柱底，地震时结构吸收的能量可以靠梁端塑性铰来耗散。此时，柱的抗弯刚度要大于梁的抗弯刚度，符合抗震设防的“强柱弱梁”设计原则。

图1（b）是柱端为受力薄弱部位，结构由于此部位出现塑性铰，造成过大变形而破坏。此时，结构的竖向承载力在很大程度上被削弱 ，使结构的安全储备降低。主要应用于结构竖向的刚度或强度不均匀，出现有突变的薄弱部位。

图1（c）为一种不很理想的破坏形式，即塑性铰可能出现在柱端、梁端，或是两个部位同时出现。此时，结构的某些构件不满足“强柱弱梁”，需要对薄弱部位进行补强，但此种情况与实际情况较为接近。

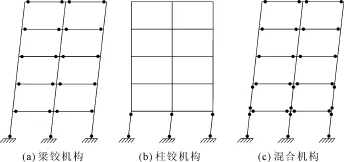
图1　结构破坏形式

1.3P-Δ效应

建筑结构在外荷载（风荷载或水平地震荷载）作用下发生水平变形 ，重力荷载因该变形而引起附加影响称为 P-Δ效应，也称为重力二阶效应。结构发生的水平侧移绝对值越大，该效应就越显著。在Push-over弹塑性分析中，对结构的最终变形也产生着重要影响。张俊发教授［13-14］曾对此展开过深入的研究，结论证明，此效应对进入屈服阶段以后的弹塑性变形影响较为显著；而规范［15］则采用增大系数法对此效应进行考虑。

2　计算实例

2.1工程概况

某学院13#学生公寓为框架结构，空心砌块填充，丙类建筑，坐落于该学院东北角，中间为内走廊，两边为阳台。地上五层，长82.5 m，宽18.42 m，层高3.6 m，建筑总高度18.45 m，建筑面积7 345 m2，共有宿舍177间，每间宿舍进深6 300 mm开间3 900 mm。建筑工程设计等级为二级，设计使用年限50 a，其平面与立面布置图见图2。

2.2数据准备

该学院所处地区为抗震设防烈度为7度，Ⅱ类场地，设计地震分组为第三组，设计基本地震加速度为0.10 g，场地特征周期为0.45 s。屋面及楼面活荷载取2.0 kN/m2，阳台活荷载取2.5 kN/m2，钢筋混凝土自重为25 kN/m2；基础混凝土强度等级采用C30，其余采用C25，环境类别为二b类；空心砌体强度为MU10，水泥砂浆为M10；受力钢筋采用三级钢，箍筋采用二级钢。采用中国建筑科学研究院PKPM研发工程部开发的空间有限元计算软件SATWE对该五层建筑进行了计算、配筋。

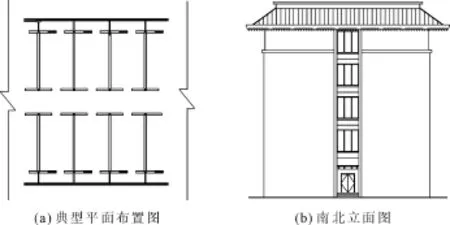
图2　公寓布置图

2.3计算结果

为了简化计算，本算例将阳台与卫生间的外墙假定为一条轴线（两者墙体中心轴线相差360 mm），并将屋顶假定为平屋顶（不计坡屋顶的高度），则其计算简图见图3，梁、柱采用杆单元，板采用壳单元，均采用程序默认网格划分。为了便于观察，取二个横向轴线间的标准部分为研究对象，见图4。

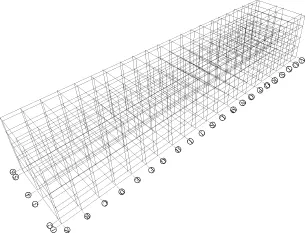
图3　整体计算图

该学生公寓仅为5层，楼高相对较低，不计 PΔ效应；采用倒三角荷载分布；破坏形式使用混合机构，即采用程序默认铰属性 ，将弯矩塑性铰属性赋予梁的两端，轴力和弯矩相关铰属性赋予柱两端。

由图5与图6可知，该公寓侧移呈剪切型。究其原因，此结构侧向刚度有限 ，其梁和柱的弯曲变形所产生的位移要大于柱的轴向变形产生的位移，前者令侧移呈剪切型，即自下而上，逐次变小，后者恰恰相反，使侧移呈现弯曲型，但前者占主要因素。各层的层间位移分布如图7所示，由图7可知，

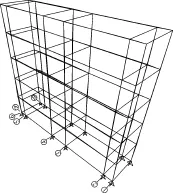
图4　计算简图

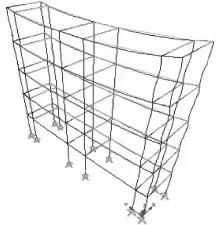
图5　变形后形状

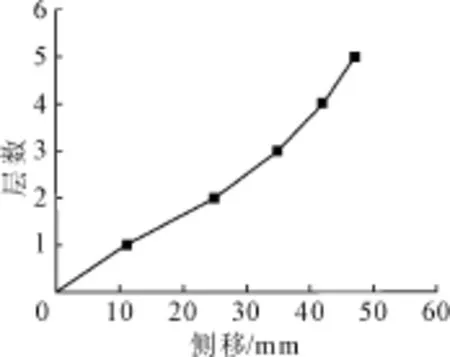
图6　各层侧移图

第二层层间位移最大，为13.72 mm，按《高层建筑混凝土结构技术规程》［15］（JGJ3—2010）的规定，薄弱层尚需进行弹塑性层间位移角的计算，即：

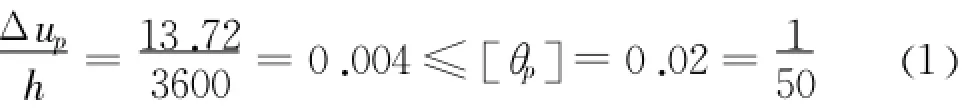
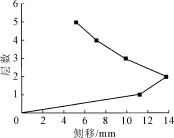
图7　层间侧移图

经计算 ，位移均符合要求，满足规定，且安全储备相对较高。

塑性铰最早出现在第二层的梁端，依次经历第一层与第三层梁端、第一层柱端，然后在梁端与柱端大批涌现，最终状态如图8所示。由图8可以看出，塑性铰主要分布在梁端，但在柱端也出现了个别柱铰，充分的说明了在设计配筋过程中，虽然在计算内力时进行了弯矩调幅以达到“强柱弱梁”的要求，但并不能完全的保证结构在弹塑性阶段完全符合抗震的要求。

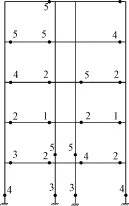
图8　塑性铰分布

Push-over曲线，即底部剪力与顶点位移曲线，是结构在地震力作用下安全性的直观表示 ，见图9。

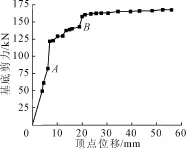
图9　Push-over曲线

由图9可知，在最初阶段（A点，Δ＜6.97 mm），整个结构呈弹性，即此阶段需进行弹性分析 ，应满足结构弹性的规定；AB段为结构由弹性向塑性过渡的阶段，即此时塑性逐渐发展并累积，剪力的增长变缓；当顶点位移超过了 B点，即Δ＞18.91 mm后，结构的基底反力增长不大，但位移持续增长，此阶段主要依靠的是塑性铰在进行耗能。

3　小　结

Push-over分析概念清晰 ，操作方便，能够很直接的找出薄弱层的位置，是日益普及应用的静力弹塑性计算方法。在运用过程中，侧向荷载形式、塑性铰的指定以及 P-Δ效应都对结果产生至关重要的影响。因此，不同的结构形式，依据不同的简化模式，运用什么样的参数设置是值得去研究的课题。文中以框架结构为例，阐述了弹塑性分析的计算程序，并使计算结果与规范的要求对比，得出了较为满意的结果。但Sap2000程序仅提供了梁、柱单元，如何把墙单元很好的去转化还是今后主要的研究方向 。

参考文献：

［1］谢礼立，马玉宏.基于抗震性态的设防标准研究［J］.地震学报，2002，24（2）：200-209.

［2］柳春光，林皋.桥梁结构push-over方法抗震性能分析［J］.大连理工大学学报，2005，45（3）：395-400.

［3］邹勤，马玉宏，崔杰.近海隔震桥梁基于性态的抗震设防标准［J］.自然灾害学报，2014，23（1）：57-63.

［4］陈小飞，马玉宏.村镇建筑基于性态的抗震设防标准研究［J］.土木工程学报，2012，45（1）：307-311.

［5］王振宇，徐岳.基于Push-over分析方法的钢框架静力弹塑性分析［J］.合肥工业大学学报：自然科学版，2014，37（10）：1249-1253.

［6］汪金祥，肖亚明，刘顺，等.基于Push-over原理的混凝土曲线梁桥抗震性能分析［D］.西安：长安大学，2011.

［7］中华人民共和国住房和城乡建设部.GB50011-2010.建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.

［8］杨 溥 ，李英民，王亚勇 ，等.结构静力弹塑性分析（push-over）方法的改进［J］.建筑结构学报，2000，2l （1）：44-51.

［9］汪大绥，贺军利，张风新.静力弹塑性分析（Push-over Analysis）的基本原理和计算实例［J］.世界地震工程，2014，20（1）：45-53.

［10］黄鑫.Push-over的研究与应用［D］.青岛：青岛理工大学，2007.

［11］肖攀，何放龙 .钢筋混凝土框架结构三维Push-over分析［D］.长沙：湖南大学 ，2009.

［12］史庆轩.钢筋混凝土基于性能的抗震研究及破坏评估［D］.西安：西安建筑科技大学，2009.

［13］朱丽佳，张俊发 ，闻建军.钢筋混凝土框架结构考虑 P -Δ效应的Push-over分析［J］.西安理工大学学报，2005，21（2）：212-215.

［14］朱丽佳，张俊发.考虑 P-Δ效应的钢筋混凝土框架结构Push-over分析［D］.西安：西安理工大学，2005.

［15］中华人民共和国建设部.JGJ3-2010.高层建筑混凝土结构技术规程［S］.北京：中国建筑工业出版社，2010.

中图分类号：TU313.1

文献标识码：A

文章编号：1672—1144（2015）03—0087—04

DOI：10.3969/j.issn.1672-1144.2015.03.017

收稿日期 ：2014-11-18修稿日期 ：2015-01-30

基金项目 ：陕西省尾矿资源综合利用重点试验室项目（2014SKY-WK014）；商洛学院科研基金项目（2014SKY-013）

作者简介 ：李涛（1986—），男，河南南阳人，硕士 ，助教 ，主要从事结构抗震方面的教学和科研工作。E-mail：litao623114@126.com

The Push-over Analysis on the 13#Students’Apartment Building of a University

LI Tao
（College of Urban，Rural Planning and Architectural Engineering，Shangluo University，Shangluo，Shaanxi 726000，China）

Abstract：Static elasto-plastic analysis（Push-over analysis）method is being accepted by the majority of researchers and designers at home and abroad with its convenient operation，strong practicality and high accuracy.Based on the basic principle of Push-over，the setting of certain parameters were discussed，such as lateral load pattern，failure form，P-Δ effect etc.，which had significant impacts on the analysis results.And then，a simple calculation was performed on a frame structure based on the setting of appropriate parameters with the finite element software Sap2000 v15.The results were in well agreement with the existing research results.The study indicates that the static analysis of similar structures using this software can meet the corresponding code requirements with a high safety coefficient.

Keywords：static elasto-plastic analysis；lateral load；failure form；P-Δ effect；plastic hinge