FRP筋混凝土梁受弯性能影响因素的有限元分析

李宝磊，宋　力，樊　成，王家祥

（大连大学材料破坏力学数值实验研究中心，辽宁大连116622）

FRP筋混凝土梁受弯性能影响因素的有限元分析

李宝磊，宋力，樊成，王家祥

（大连大学材料破坏力学数值实验研究中心，辽宁大连116622）

摘要：目前越来越多的纤维增强塑料筋（FRP）被应用于土木工程当中，把FRP筋作为一种钢筋的替代品。FRP筋的屈服点不明显而且其弹性模量也比较低，这就造成了荷载下的FRP筋混凝土梁会产生较大的变形和裂缝宽度。为了研究影响FRP筋混凝土梁受弯性能的各方面因素 ，采用大型通用有限元分析软件ABAQUS对配有FRP受拉筋的混凝土梁进行建模并分析其受弯性能。数值模拟结果与他人的实验结果有较高的吻合度，同时分析了影响FRP筋混凝土梁受弯性能的一些因素。

关键词：FRP筋；荷载-位移曲线；混凝土梁；受弯性能；ABAQUS

纤维增强塑料筋（FRP）是由纤维和树脂在加入一定的调和剂的情况下经过拉拔成型和表面处理而形成的一种性能优越的钢筋替代材料，具有诸多优点［1-2］。国家每年都要将大量资金用于维修或者更换被一些具有腐蚀性的介质（酸、碱）侵蚀而造成破坏的钢筋混凝土构件。用FRP筋代替一些混凝土结构（比如梁、板）的受拉钢筋是解决其发生锈蚀的行之有效的办法，进而可以在建筑工程领域中大量使用。由于FRP筋有抗磁性的特殊优点，可以将其应用于对抗磁有特殊要求的建筑结构。目前常用的FRP筋有三种，分别是玻璃纤维增强筋（GFRP），碳纤维增强筋（CFRP）和芳纶纤维增强筋（KFRP），它们在拉断前的应力应变关系一直是保持线弹性变化的。

国外，Cosenza E等［3］在2001年对FRP静混凝土梁进行了实验研究并提出了能够适用于FRP筋混凝土梁的最大裂缝宽度计算公式和其极限值。Tighiouart B［4］和Abdalla［5］等人的实验取得了一些重要成果，如加载位置，加载类型以及保护层厚度等能够在一定程度上影响FRP筋和混凝土之间的相互作用。我国对于FRP筋的研究起步较晚，但是发展的速度很快。济南大学的徐新生［6］教授在2009年对FRP筋混凝土梁的受弯性能进行了多组实验研究，分析了影响FRP筋混凝土梁受弯性能的因素，并用有限元软件ANASYS进行了数值模拟。

有限元软件ABAQUS以其简单的可视化的操作界面和其计算快、精度高的特点被广泛的应用于科研领域和具体的实际工程。相对于其它的有限元软件，ABAQUS对混凝土构件的非线性分析能够得出更为贴近实验的结果［7］。本文用数值方法对FRP筋混凝土梁从加载开始直到构件破坏的全过程进行非线性分析，重点考虑了影响FRP筋和混凝土相互作用的几个主要方面，为深入研究FRP筋混凝土梁提供了依据。

1　有限元分析

在ABAQUS中模拟FRP筋和混凝土的非线性特性需要分别定义其材料的 σ-ε关系。弹性阶段须输入材料的弹模、泊松比；在塑性阶段，FRP筋和在弹性阶段的设置一样保持不变，而混凝土则需要选择塑性模型来定义其应力应变关系［8］。ABAQUS中有三种塑性模型［9］可供选择，分别是混凝土裂缝模型，混凝土弥散开裂模型和混凝土塑性损伤模型，其中塑性损伤模型在单向加载和循环加载方面有一定的优势并且容易收敛，因此本文采用混凝土塑性损伤模型来定义混凝土的塑性变形。

1.1应力应变关系

1.1.1混凝土σ-ε

受压时σ-ε关系用如下表达式［10］：

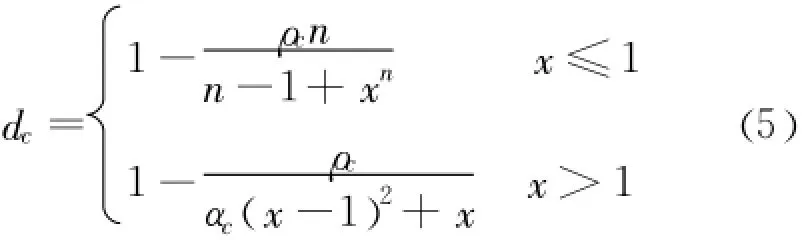
式中参数根据规范［11］取值 ，fc，r表示立方体抗压强度标准值；dc是混凝土塑性损伤因子。

受拉时 σ-ε关系采用如下公式［12］：

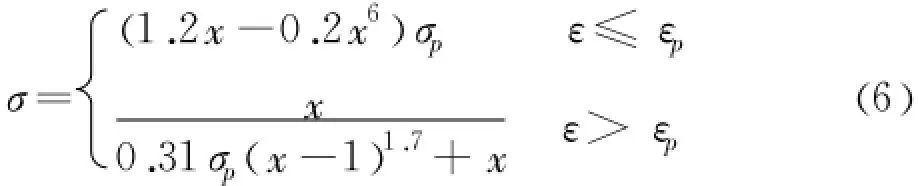
式中 ，σp=0.26（1.25fc′）2/3，

εp=43.1σp，X=ε/εp

1.1.2FRP筋σ-ε关系

FRP筋σ-ε表达式为σf=Efεf，关系曲线见图1。

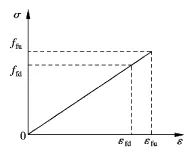
图1　FRP筋应力应变关系曲线

1.2建模

如图2所示，为整体有限元模型。

图2　FRP筋混凝土梁有限元模型

1.2.1参数设定

塑性损伤模型中塑性模块中的参数参考文献［10］，Viscosity parameter=0.0005，随着黏滞系数取值的增大模型更容易收敛，但是模型的计算精确性会有所降低。由于本文建模时选用的是塑性损伤模型，所以还需要计算出混凝土拉压非弹性应变（εck、εin）与相应的损伤因子（dt、dc）之间的关系，见公式（7）：

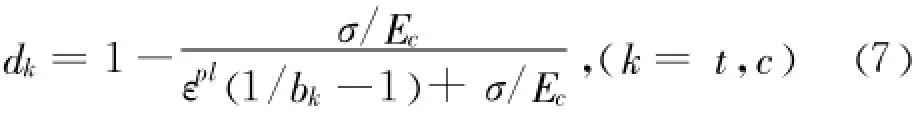
其它的需要输入的参数见表1、表2、表3［10］。

表1　混凝土参数

表2　钢材参数

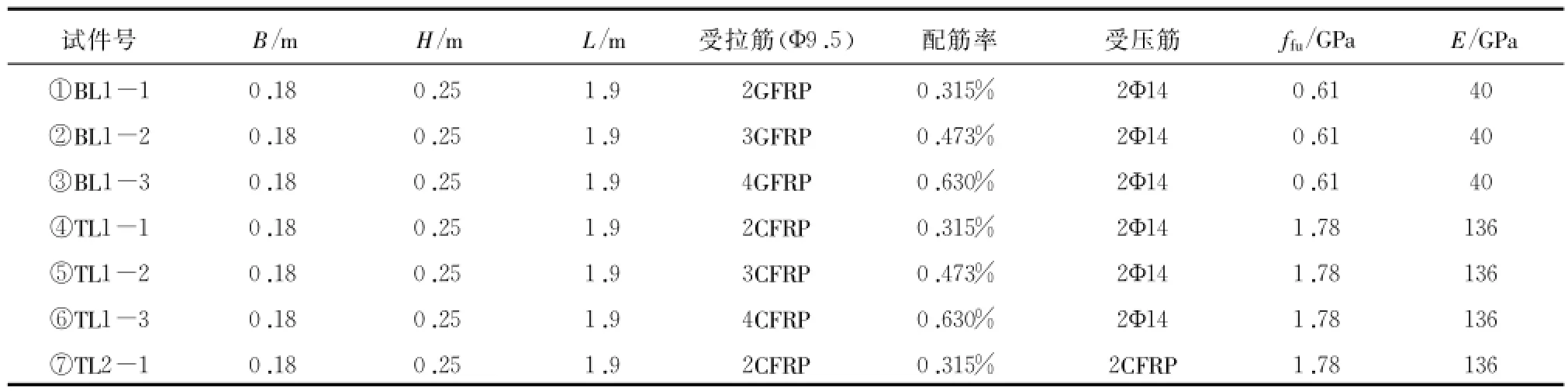
表3　试件尺寸及配筋

1.2.2单元划分、边界条件及荷载施加方式

为了保证单元划分的均匀，本文采取的是边缘撒种子分步划分的方式对模型进行单元划分。混凝土单元采用C3D8R，FRP筋采用T3D2。

考虑到试验过程中的加载方式，本文在模型的支座处和加载处分别设置了刚性垫块，刚性垫块和混凝土梁采用Tie的连接方式，这样做能够避免形成应力集中现象。将梁的其中一个支座的全部自由度约束，另一个支座不约束 X方向自由度，整体形成一个简支梁的形式。支座约束设置在刚性垫块的底面中线上，保证梁在受弯过程中能够发生转动。采用等效位移控制的原则在模型梁的1/3处施加对称荷载。

1.3模型验证

利用上述的建模方法建立文献［13］中试验梁的有限元模型并进行数值模拟计算，得到的 F-D曲线的对比情况见图3～图5。

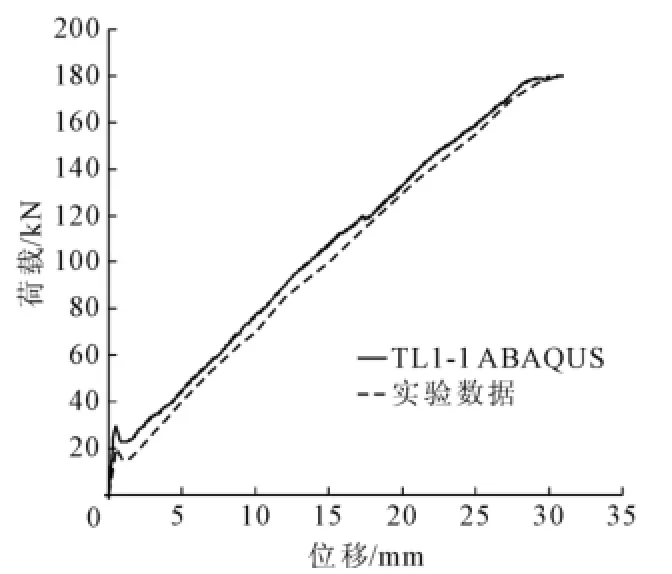
图3　TL1-1 F-D对比

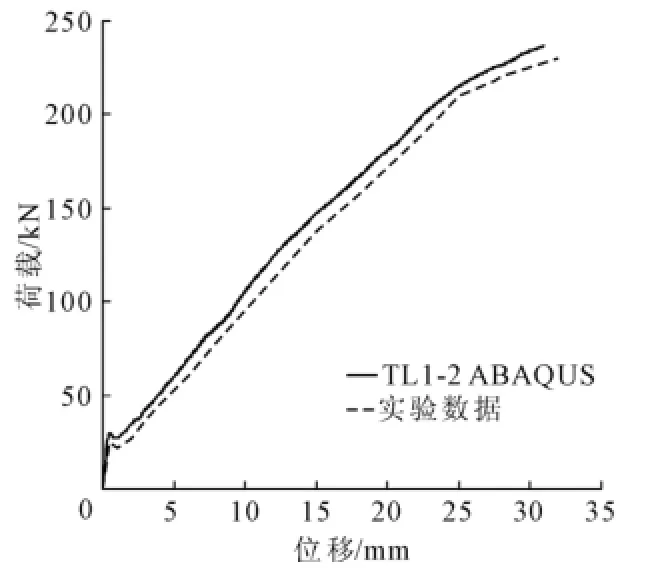
图4　TL1-2 F-D对比

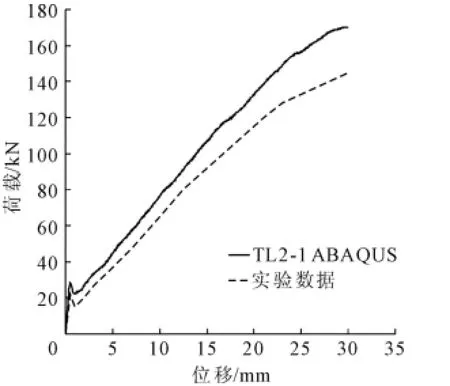
图5　TL2-1 F-D对比

从图3～图5中能够观察到数值模拟得出的结果和文献［13］的实验结果基本一致，这说本文的建模方法和材料σ-ε关系的选取是正确的。

2　FRP筋混凝土梁受弯影响因素有限元分析

本文将从FRP筋配筋率、FRP筋的类型、混凝土强度、混凝土保护层厚度、截面高度等几个方面来考虑对FRP筋混凝土梁受弯性能的影响。

2.1FRP筋配筋率

不同配筋率的 F-D图见图6、图7。

从图6、图7中可以看出FRP筋混凝土梁的承载力受FRP筋配筋率的影响较大。其承载力随着配筋率的增大而提高。由于在混凝土开裂前的梁底部的拉力主要有混凝土来承担，因此开裂荷载不受配筋率的影响，没有变化。随着位移加载不断增大，FRP筋混凝土梁的刚度表现为逐渐降低，但是配筋率大的梁刚度降低的要小。

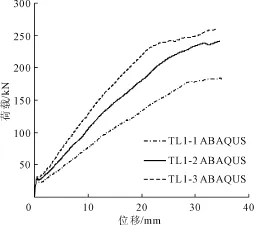
图7　不同配筋率的TL梁 F-D对比图

图6中GFRP筋混凝土梁（BL1-1，BL1-2，BL1 -3）整体承载能力提高约35.77%。图7中CFRP筋混凝土梁（TL1-1，TL1-2，TL1-3）的整体承载力提高相对较小，约25.15%。

短期基准面下降晚期，三角洲推进作用逐渐明显。大量沉积物沿湖盆边缘斜坡发生坡移，与地形坡折背景相配置时，可在深水湖区发生再沉积作用形成浊积扇。基准面开始上升时，浊积扇沉积物保存下来，称为坡移浊积扇。坡移浊积扇分布范围、砂体厚度均较大，一般厚度为10～20m，粒度较粗，为含砾砂岩、砂岩沉积。平面上，浊积扇可沿三角洲前方的深水湖区呈群状分布。当三角洲进积作用较强时，产生坡移浊积扇的可能性较大（图2）。

2.2FRP筋类型

把试件①和试件④设为A组，试件②和试件⑤设为B组。在这两组试件中，只考虑的FRP受拉筋类型这一因素，其 F-D曲线见图8、图9。从图8、图9中能够看出在梁发生相同位移的情况下CFRP筋混凝土梁要比GFRP筋混凝土梁的承载力高出许多。TL1-1比BL1-1整体提高1.66%，TL1-2比BL1-2整体提高1.57%。出现这种情况的主要原因是CFRP筋的平均拉应力以及极限拉应力都要高于GFRP筋，而在梁底部混凝土开裂后的拉应力又几乎完全由FRP筋承担。图中的 F-D曲线斜率相对较小，这说明它的延性相对于钢筋混凝土梁来说要差一些。虽然会有较大的变形，但这对于其整体使用功能的影响是微小的，而且我们能够通过其它有效措施提高其延性，如进行混合配筋加入受拉钢筋等。

2.3混凝土强度的影响

图10是试件在其它参数都相同而只考虑混凝土强度这一影响因素下得出的荷载-位移曲线。混凝土强度分别取C30、C40、C50。从图10（a）、图10 （b）、图10（c）中可以看出提高混凝土强度对开裂荷载有一定提高，但对梁的整体受弯性能影响不大，这主要是因为混凝土强度对试件刚度的影响有限。在施加荷载初期，三种不同混凝土强度下的位移比较接近，随着荷载继续增加，强度高的混凝土梁位移增加相对缓慢。

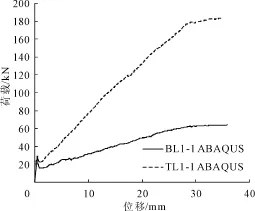
图8　BL1-1和TL1-1 F-D曲线对比

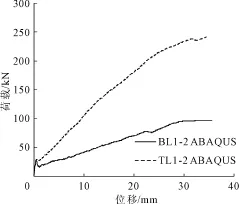
图9　BL1-2和TL1-2 F-D曲线对比

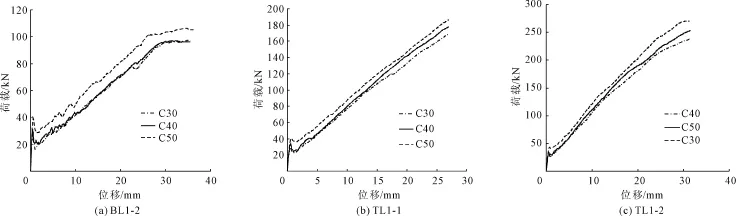
图10　试件在不同混凝土强度下的 F-D曲线

2.4混凝土保护层厚度的影响

图11、图12是试件②、⑤只考虑保护层厚度这一影响因素对FRP筋混凝土梁受弯性能的影响。从图中可以看出，在梁底部混凝土开裂前 ，保护层厚度的改变对梁承载力几乎没有影响。

图11　BL1-2不同保护层的 F-D曲线

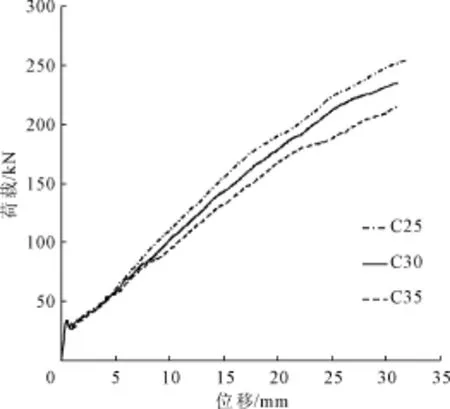
图12　TL1-2不同保护层的 F-D曲线

2.5截面高度的影响

图13，图14分别是试件②BL1-2和试件⑤TL1 -2只考虑截面高度对FRP筋混凝土梁受弯性能的影响下得出的荷载位移曲线。在进行数值模拟时只改变截面高度，其余参数不变，截面高度分别取 h= 250 mm，h=300 mm和 h=350 mm。模拟结果如图13、图14所示：截面高度对FRP筋混凝度梁受力性能影响很大，试件②BL1-2的承载力随着截面高度的增大平均提高41.62%，试件⑤TL1-2的承载力随着截面高度的增大平均提高38.66%。这是因为增大截面高度的同时就会增大截面的惯性矩，从而进一步增大梁的抗弯刚度 ，进而减小位移［14］。在工程应用中，如果截面尺寸受到限制，可以适当的增加配筋率和施加预应力来满足要求。

图13　BL1-2不同截面高度的 F-D曲线

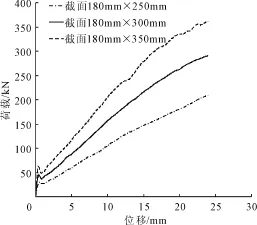
图14　TL1-2不同截面高度的 F-D曲线

3　结　论

（1）用ABAQUS建立的有限元模型可以贴近真实的模拟整个梁的受弯过程，计算得出的 F-D曲线与实验结果得出的曲线的吻合度较高。

（2）FRP筋混凝土梁受弯性能受FRP筋类型和梁的截面尺寸影响较大，而受保护层厚度和混凝土强度的影响较小。增大保护层厚度还会对其承载能力产生不利影响。

（3）本文存在的主要问题是在用ABAQUS进行有限元分析时直接将钢筋嵌入（Embedded）到混凝土当中，这会导致计算值比真实值偏高，但是这对整体了解FRP筋混凝土梁的受弯过程是有一定帮助的。

参考文献：

［1］张建伟，邓宗才，杜修力 ，等.预应力FRP在混凝土结构中的应用研究与发展［J］.世界地震工程，2006，22（1）：133-139.

［2］王茂龙，朱浮声，金延.预应力FRP筋混凝土梁受弯性能试验研究［J］.混凝土 ，2006，（12）：35-38.

［3］Cosenza E B，Manfredi G，Realfonzo R.Behavior and modeling of bond of FRP rebars to concrete［J］.American Society of Civil Engineers，1997，1（2）：40-51.

［4］Benmokrane B，Tighiouart B，Chaallal O.Bond strengthand load distribution of GFRP reinforeing bars in concrete［J］. ACI Materials Journal，1996，93（3）：246-253.

［5］Wegian F M，Abdalla H A.Shear capacity of concretebeams reinforced with fiber reinforced polymers［J］.Composite Structures，2005，71（1）：130-138.

［6］徐新生，曹凯，闫玉本.FRP筋混凝土梁的挠度特点及影响因素分析［C］//第19届全国结构工程学术会议论文集，2010.

［7］刘劲松，刘红军.ABAQUS钢筋混凝土有限元分析［J］.装备制造技术 ，2009，（6）：69-70.

［8］王丽，邓思华.基于ABAQUS的混凝土梁受弯破坏实验非线性分析［J］.土木建筑工程信息技术，2010，2（1）：64-67.

［9］庄茁 ，张帆，岑松.ABAQUS非线性有限元分析与实例［M］.科学出版社，2005.

［10］李宝磊，宋力，樊成，等.FRP筋混凝土梁受弯性能的数值分析［J］.山西建筑，2015，41（5）：22-24.

［11］中华人民共和国建设部.GB50010—2010.混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［12］沈聚敏，王传志 ，江见鲸.钢筋混凝土有限元与板壳极限分析［M］.北京：清华大学出版社，1993.

［13］徐新生，纪涛，郑永锋.FRP筋混凝土梁挠度的特点及计算方法［J］.工程力学，2009，26（S1）：171-175.

［14］郑永峰.FRP筋混凝土梁受力性能的试验研究及有限元分析［D］.济南：济南大学，2008.

中图分类号：TU377.9

文献标识码：A

文章编号：1672—1144（2015）03—0100—05

DOI：10.3969/j.issn.1672-1144.2015.03.020

收稿日期 ：2014-12-23修稿日期 ：2015-02-25

作者简介 ：李宝磊（1986—），男，山东德州人，硕士研究生，研究方向为混凝土结构。E-mail：107648255@qq.com

通信作者 ：宋力（1959—），男，辽宁大连人，博士 ，教授 ，主要从事岩石、混凝土等工程材料弹塑性损伤的基本理论与数值试验研究。E-mail：songli-500@163.com

Finite Element Analysis of the Bending Performance Influencing Factors of FRP Reinforced Concrete Beams

LI Bao-lei，SONG Li，FAN Cheng，WANG Jia-xiang
（Research Center for Numerical Tests on Material Failure，Dalian University，Dalian，Liaoning 116622，China）

Abstract：Nowadays FRP bars are widely applied in the civil engineering structures as a substitute of steel bars.The low elastic modulus and non-yielding characteristics of FRP bars result in large deformations and wide cracks in concrete beams reinforced with these bars under loading.In order to study the factors that influencing the bending performance of FRP reinforced concrete beams，the finite element software ABAQUS was used to establish a model of this beam and its bending properties was analyzed as well as the influencing factors.The results of the numerical simulation are in good agreement with the experimental results of other researchers.

Keywords：FRP bars；load-displacement curve；concrete beam；bending performance；ABAQUS